一种基于聚类的卫星太阳电池阵衰减估计方法
曹孟达,张 涛,李训嘉,刘亚杰
(国防科技大学 系统工程学院,湖南 长沙 410073)
0 引言
太阳电池阵—蓄电池电源系统是目前国内航天器主要采用的电源系统。因此,近地卫星在轨运行中基本都需要太阳为其提供能源[1]。卫星太空运行的能源主要由卫星太阳电池阵的光电转换工作来实现[2]。太阳电池阵是卫星电源系统的重要电源,在光照期,太阳电池阵的输出功率分成2部分,一部分供给负载,另一部分经充电器对蓄电池组进行充电[3],而地影[4]时期由蓄电池组对卫星提供能源。太阳电池阵在太空中的输出功率一般来讲都不是稳定不变的,能够对太阳电池阵的输出功率产生影响的因素可概括为以下几个方面:① 工作温度,太阳电池阵光伏发电核心单元为硅太阳能电池,太阳能电池短路,电流随温度的升高而升高,而太阳能电池的峰值功率随温度的升高而降低。即温度每升高1 ℃,太阳能电池的峰值功率损失率约为0.135%~0.145%;② 太阳光照强度,主要受日地距离因素和太阳入射角等影响;③ 空间环境,如:粒子辐照、紫外辐照、微流星体碰撞和冷热交变等衰减[5-7]因素。前2种主要为周期性变化,第3种呈现为长期性的衰减变化,对卫星寿命[8-10]有较大影响。因此,应实时估算太阳电池阵受太空中多种环境因素影响而造成的衰减情况,其衰减估计既用于太阳电池阵寿命预测,又可为太阳电池阵的设计提供理论参考。
本文以某太阳同步轨道卫星太阳电池阵12个月的在轨数据为基础,以聚类方法得到太阳电池阵的温度、日地距离和太阳入射角度等同状态数据,对同状态点的电流值进行周期性补偿,消除周期性后拟合数据得到太阳电池阵的在轨衰减估计。该方法能够以短时间内卫星在轨数据进行实时衰减估计,既可用于卫星发射初期对太阳电池阵的工作状态进行分析,也可用于卫星运行中末期对太阳电池阵寿命及工作年限进行估计,能够为太阳电池阵的在轨健康状态管理提供依据。
1 国内外研究现状分析
伴随航天事业的快速发展,太空中卫星数量逐年增加,需要建立故障排查报警、快速分析处理以提高卫星在轨安全运行能力[11]。电源是卫星的重要分系统,当供电系统出现问题,将会导致卫星无法正常工作。太阳电池阵是卫星电源系统中在光照期负责对卫星进行电力供应并对在阴影区负责电力供应的蓄电池进行充电,因此关注太阳电池阵的运行状况,对提高卫星在轨运行的可靠性和寿命[12]具有重要意义。
现有的对在轨卫星的太阳电池阵研究总体可以分为3类:特殊点法、归一化公式法和定性分析法。① 特殊点法采用太阳电池阵多年全年电流最低点夏至日数据,拟合出太阳电池阵衰减规律。李强、李剑锋[13]等对多年LEO(近地球轨道)卫星分至日前后的太阳电池阵输出电流进行采样分析,通过对分至日前后的电流取均值得到多年夏至日为电流最低点,选择拟合多年夏至日点电流得到太阳电池阵衰减估计。刘震、杜红[14]等对太阳电池阵总输出电流作图发现,每一年电流的变化规律呈马鞍形,两峰点为春分和秋分,鞍部为冬至,由于日地距离在一年中变化规律为冬至<春分<秋分<夏至,全年总输出电流的最低点为夏至[15]。而太阳电池阵的最低输出功率也是卫星正常工作的基本保障,因此,通过易于观测的全年的最低总输出电流点(夏至点),以多年夏至点总输出电流进行曲线拟合得到太阳电池阵逐年衰减率估计。② 归一化公式法关注太阳电池阵某时刻电流和发电阵使用初期电流与温度、太阳入射角、日地距离因子、衰减因子(使用初期为1)影响因素的关联性。彭梅、王巍巍[11]等通过太阳电池阵输出电流的表达公式,对太阳电池阵工作温度、太阳入射角和日地距离因子等影响参数归一化后得到太阳电池阵每月的输出电流,将每月输出电流同初期未衰减状态的太阳电池阵输出电流作比,得到太阳电池阵的逐月衰减估计。③ 定性分析法则不局限对太阳电池阵衰减估计,观察卫星太阳电池阵的一个完整发电周期太阳电池阵,分析太阳电池阵输出功率周期内产生变化与地球反照、星体遮挡和温度的关系。井元良、孙海涛[15]等提出了对一年内电流值在太阳入射角、地日距离因子和温度因素上归一化后利用指数拟合,得到衰减因子,但仅有结果,未给出方法与过程。
3类方法中特殊点法与归一化公式法均需要卫星多年在轨数据拟合衰减估计,但当太阳电池阵出现局部故障导致太阳电池阵无功率输出时,此时特殊点法或归一化公式法都无法保证衰减估计的准确性。刘震、杜红等人[14]提出一种曲线平移法以消除其故障对太阳电池阵分析造成的影响。定性分析法则关注周期内变化,但无法给出电池阵衰减的定量分析过程。
因此,结合彭梅等人提出的归一化公式法,能够发现不断将太阳电池阵输出电流公式中各个参数归一化的实质在于消除其对输出电流的影响,保证输出电流在某参数方面可以视为同状态。而特殊点法选择全年总输出电流的最低点夏至的意义则同样是保证在每年的夏至时刻可认为温度、日地距离等影响因素为同状态参数。因此,基于寻找太阳电池阵同发电工况点,提出一种综合性方法,先基于卫星与归一化公式法中归一化的温度、太阳入射角和日地距离因子等参数的相关数据进行聚类,得到同发电工况点。对太阳电池阵输出电流进行周期识别后得到电流每时刻的周期性补偿,将同发电工况点的电流值进行周期补偿后拟合衰减。经实验验证,该方法能够利用短时间的卫星在轨数据得到较准确的太阳电池阵衰减估计。
2 基于聚类的太阳电池阵衰减评估方法
2.1 太阳电池阵工作机理
基于卫星是一颗在轨的低轨太阳同步轨道卫星,其太阳电池阵在光照期负载卫星运行和为在阴影区时供电的蓄电池充电。由于卫星采用局部-线性-顺序分流调节的控制方式来保证稳定的母线电压,因此卫星的太阳电池阵输出电压由负载卫星运行的母线电压、太阳电池阵至母线通路上的电缆及接揽件平均压降和隔离二极管压降3部分组成[11]。经过在轨数据查询,卫星母线电压全年变化在0.8 V以内,隔离二极管压降与太阳电池阵上电缆及接插件平均压降为固定常量,因此卫星的太阳电池阵的输出电压可基本视为常量。太阳电池阵在电源系统的分流调节控制方式下,太阳电池阵的输出功率可以由太阳电池阵的输出电流表征。
太阳电池阵输出功率一般用太阳电池阵I[16-17]表示,即
I=F·FS·[IBOL+β(T-25)]·cosφ,
式中,IBOL为寿命初期在25 ℃工作温度、从单位日地距离0°入射时的太阳电池阵输出电流,单位A;β为电流温度系数,单位A/℃;φ为太阳入射角,单位(°);F为功率系数,无量纲;FS为日地距离因子,无量纲。
从输出电流表达式能够发现太阳电池阵的温度、日地距离因子、太阳入射角是造成影响的重要因素。从理论上来讲,只需要找到一系列同等条件下(温度、日地距离和太阳入射角)太阳电池阵的输出电流,对同发电工况输出电流点以时间为x轴进行衰减拟合就能得到太阳电池阵的衰减估计;但由于卫星不同,采样数据不同,因此以输出电流表达式中的参数为参考,通过分析其不同参数对太阳电池阵的影响方式以及相关度分析,找到输出电流表达式中电影的3类参数进行聚类得到同发电工况的输出电流,能够进行太阳电池阵的衰减估计。
2.2 衰减评估流程
太阳电池阵衰减评估流程如图1所示。
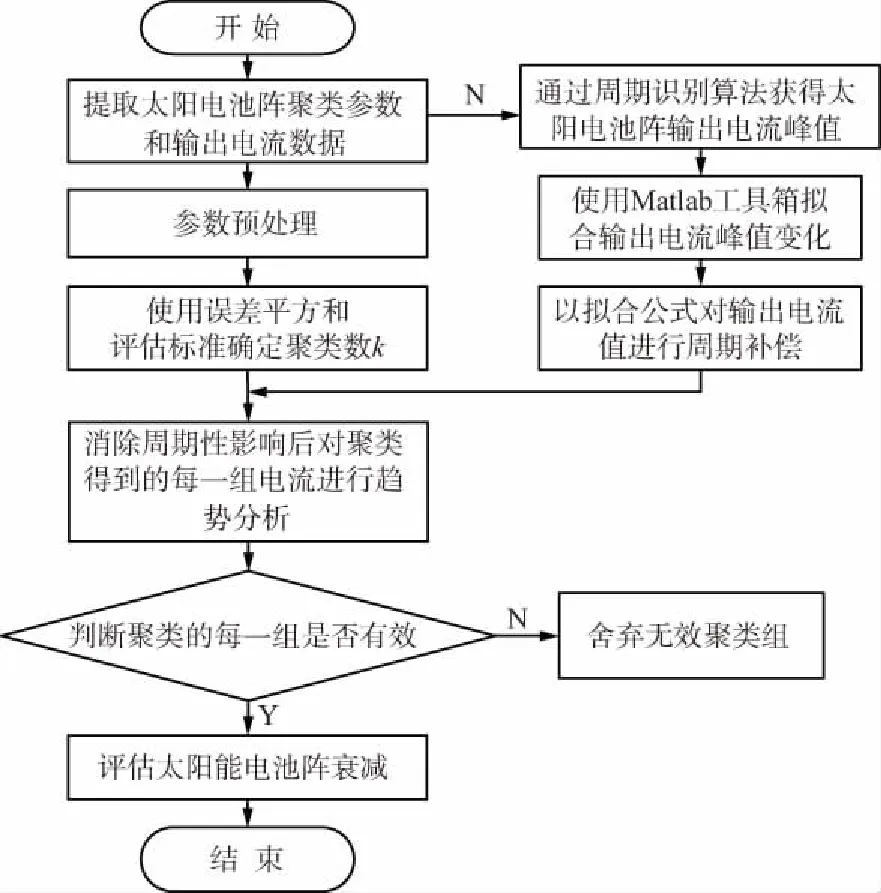
图1 拟合衰减流程
首先进行聚类参数选取和数据提取,然后分2个方面进行,一方面需要参照文献中的影响因素和进行相关度分析,选取合适的参数进行聚类,以得到消除温度、太阳入射角和日地距离因子等方面影响的同发电工况太阳电池阵输出电流;另一方面,由于太阳电池阵发电过程中还会受到太阳活动强弱[18]、地球反照[19-20]等周期性变化因素影响,因此通过对太阳电池阵输出电流进行周期识别,选取太阳电池阵波峰电流拟合出太阳电池阵对应时间的总输出电流的公式,与太阳电池阵波峰电流均值作差,能够得到对应时间的输出电流的补偿值。进行k-means聚类后,通过每一类中太阳电池阵的总输出电流对应的时间,对太阳电池阵的总输出电流与对应时间的电流补偿值作差,得到消去太阳强弱变化、地球反照影响的同发电工况输出电流。此时对得到的输出电流进行衰减拟合,得到太阳电池阵输出功率的衰减估计。
2.3 主要过程与步骤
2.3.1 参数选择与处理
在归一化公式法介绍的太阳电池阵输出电流公式中,温度、太阳入射角、日地距离因子与衰减因子是影响太阳电池阵输出的重要参数。太阳入射角和日地距离因子表示阳光照射角度、光照距离带来的太阳光量变化对输出电流的影响。工作温度则是因为太阳电池多利用硅、硒等半导体材料在进行光伏效应将光能转化为电能的过程中,会对其传导作用造成影响从而对发电量产生影响。实验初期针对文献中所提半长轴、太阳帆板驱动结构2个参数,但由于本卫星是太阳同步轨道卫星,半长轴在卫星运行过程中变化极小,故舍去该参数。而太阳帆板驱动结构原想用于表征帆板角度,但通过相关度分析,发现其相关度靠前均为状态参数,因此认为该太阳帆板驱动结构也为状态参数,故舍去。对+Y帆板输出电流进行相关度分析,能够发现温度相关度较高。而对输出角做相关度分析,则发现相关度最高的即为太阳辐射因子,0.633 1。聚类参数方面最后选择输出角ASS1、太阳电池阵帆板外板温度和内板温度的相关度求和与太阳辐射因子表征这3类参数。具体处理过程如下。
① 温度方面:选取卫星数据分析软件analysis中的太阳电池阵帆板外板温度和帆板内板温度。用太阳电池阵总输出电流对卫星的2 300多个参数进行相关度分析,帆板外板温度和内板温度相关度分别为0.930 1和0.765 1,对2类参数去除离群点然后进行相关度处理,最后进行归一化:
Tfinal=(0.930 1×tout+0.765 1×tin)/(0.930 1+0.765 1)。
② 日地距离因子:由于表征太阳光量变化,选取卫星在轨数据中的太阳辐射因子参数,去除离群点后归一化。
③ 太阳入射角:选取卫星在轨数据中表征帆板转角参数的输出角ASS1。对输出角去除离群点后归一化。然后得到用于聚类的原始数据。表1给出了部分用于聚类的原始数据。
表1 聚类原始数据

时间电流/A温度/°C输出角/cos太阳辐射因子2016/6/1 08:00:5222.710.791 3710.4680.015 686 2752016/6/1 08:41:0423.080.463 3110.4680.019 607 8432016/6/1 08:42:4823.200.594 9520.4600.592 156 8632016/6/1 08:44:3423.450.682 6810.5160.729 411 7652016/6/1 08:48:0323.690.762 1440.6080.886 274 512016/6/1 08:49:4823.320.803 3930.7920.898 039 2162016/6/1 08:53:1822.710.854 2610.7680.890 196 078
2.3.2 参数的聚类
如何使k-means聚类更好地发挥作用,得到更好的结果,取决于初始化时的聚类数k。这里使用一个简单的指标SSE(Sum of Squared Error)组内误差平方和来确定最佳聚类数目。SSE评估标准如图2所示。
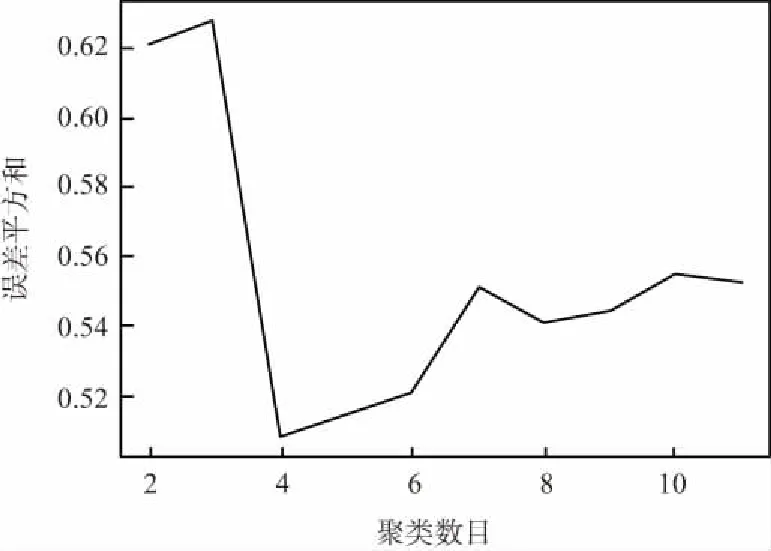
图2 SSE评估标准
随着聚类数目增多,每一个类别中的数量越来越少,距离越来越近,因此,WSS(Within Groups Sum of Squares)值是随着聚类数目增多而减少的,最优k值取决于斜率的变化,但WWS减少的很缓慢时,就认为进一步增大聚类数效果也并不能增强聚类效果。前后斜率发生骤变的点被称为肘点(knee point),这个“肘点”就是最佳聚类数目,而由图2能够发现k=4时即为肘点,同时k=4时WSS最小,因此,取k=4为聚类数据最合适的聚类数。
由于该方法属于对k进行遍历运行后打分、比较,数据集要求不能过大。因此,在聚类前,对11万余条聚类数据按时间分布每隔4条抽样选取一条,得到2万多条的小数据集进行组内平方误差和评估。
基于聚类数据集较大,且通过SSE评估标准能够得到合适的聚类数,因此选择k-means算法进行聚类,能够发挥其聚类效率高的优点,并通过误差平方和评估高标准提前确定最佳聚类数k和对聚类数据的预处理,能够得到较好的聚类效果并避免数据中噪声、离群值对k-means算法的聚类效果造成影响。
2.3.3 基于二次聚类的电流峰值提取
观察图3中卫星太阳电池阵总输出电流,能够发现其在时间维度上具有周期性。因此在对聚类后的同状态点电流拟合衰减前需消除其周期性,防止聚类得到的同发电工况点恰好在总输出电流的上升段或下降段,对衰减估计造成影响。太阳电池阵总输出电流如图3所示,周期识别流程如图4所示。
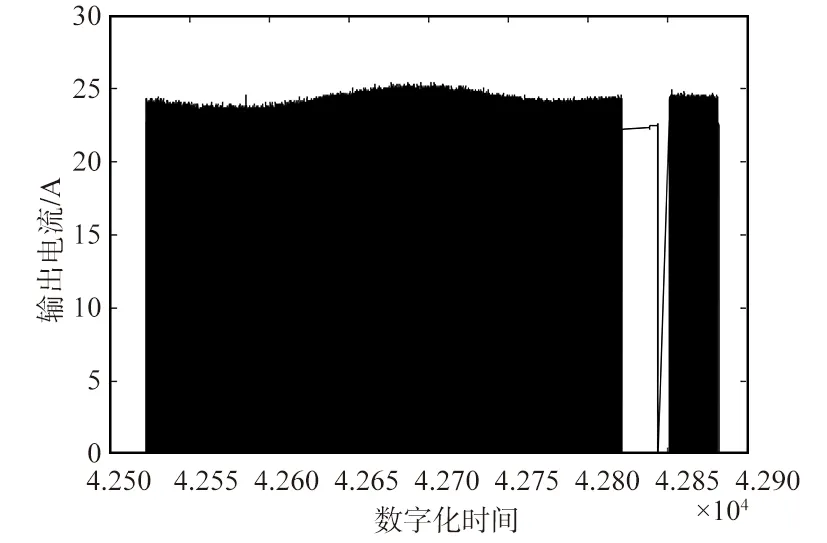
图3 太阳电池阵总输出电流
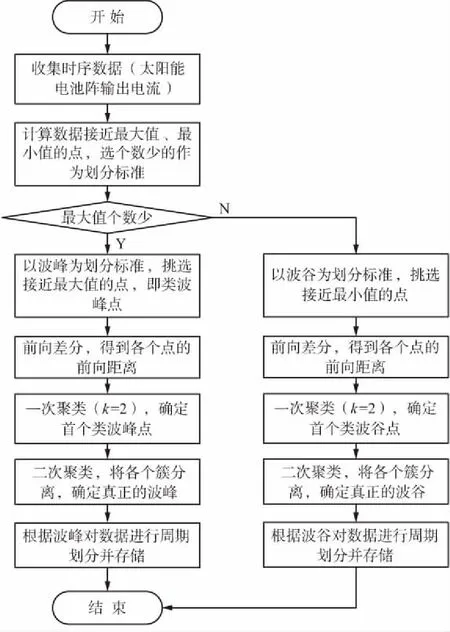
图4 周期识别流程
由于太阳电池阵总输出电流存在周期性波动,本周期识别方法通过二次聚类,得到一段时间内的波峰或波谷值,选取太阳电池阵波峰数据对聚类后同状态点电流进行去周期性处理。具体步骤如下。
步骤1:提取太阳电池阵输出电流数据,如图5所示。
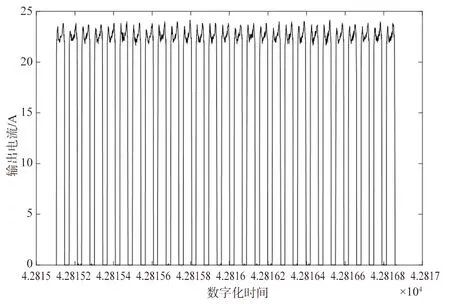
图5 太阳电池阵总输出电流
步骤2:通过制定波峰存在的阈值(此处设为大于电流最大值*0.95的区域),对输出电流值进行筛选,得到类波峰值。如图6所示,深色部分为输出电流值,浅色部分为筛选后得到的类波峰值。
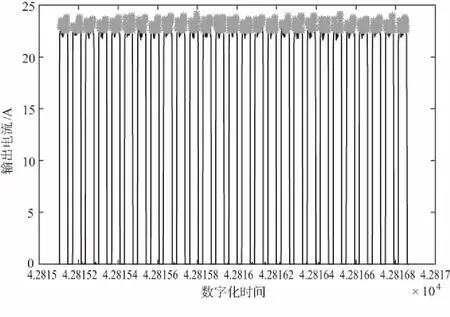
图6 设置阈值后的类波峰点
步骤3:通过前向距离差分,设置一个周期内的点之间前向距离为1,不同周期点之间前向距离为一个大数,通过一次聚类(k=2),确定每个周期的第一个类波峰点。如图7所示,深色部分为输出电流,浅色点即为输出电流中每个周期内的首个类波峰点。
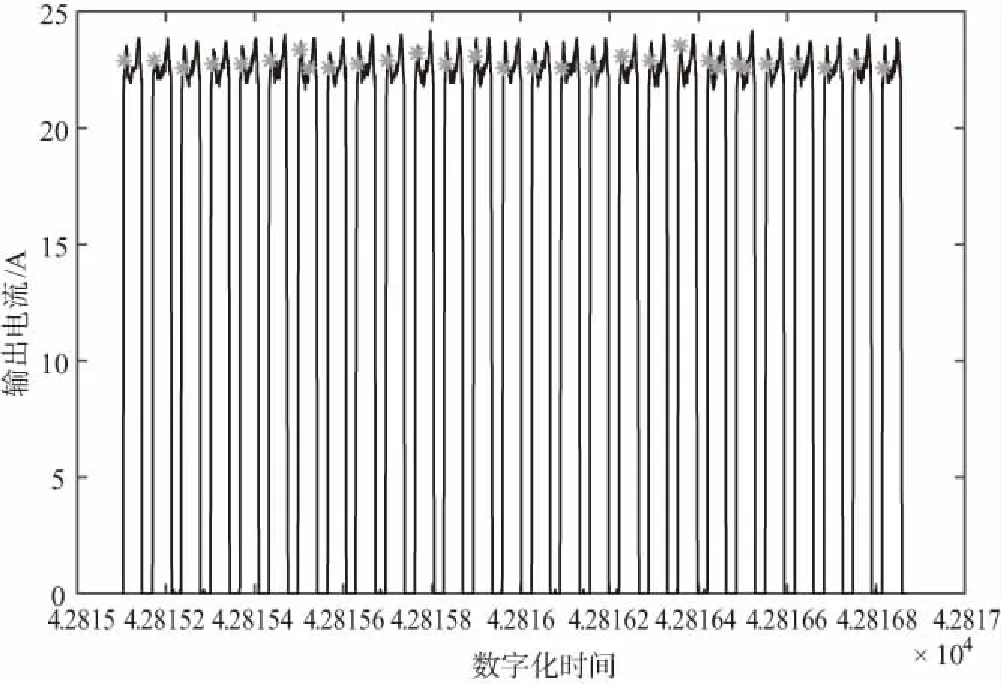
图7 通过前向距离二次聚类分离出每个周期
步骤4:以找到的首个类波峰点为聚类中心,以首个类波峰点个数为聚类数进行二次聚类,得到每个周期内全部类波峰点,再取最大值即为每个周期的波峰,如图8所示,浅色点即为最后得到的输出电流周期峰值。
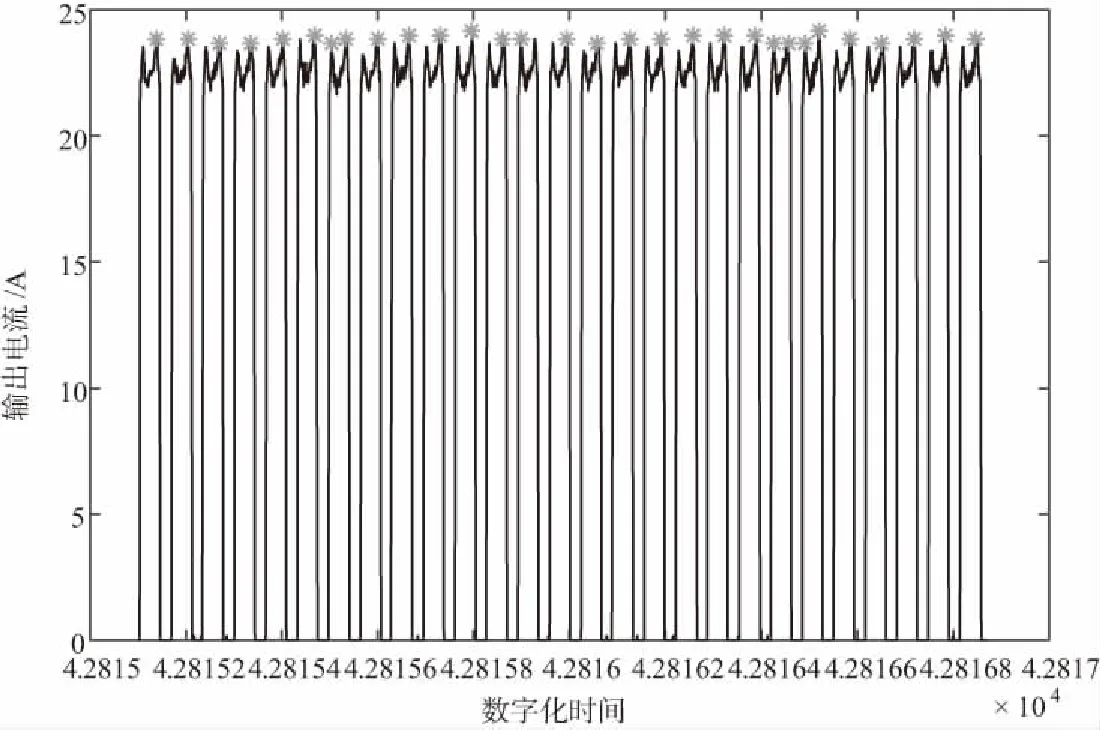
图8 每个周期内波峰点
2.3.4 电流周期性补偿
经过二次聚类,得到如图9所示的上层灰色部分的波峰数据。
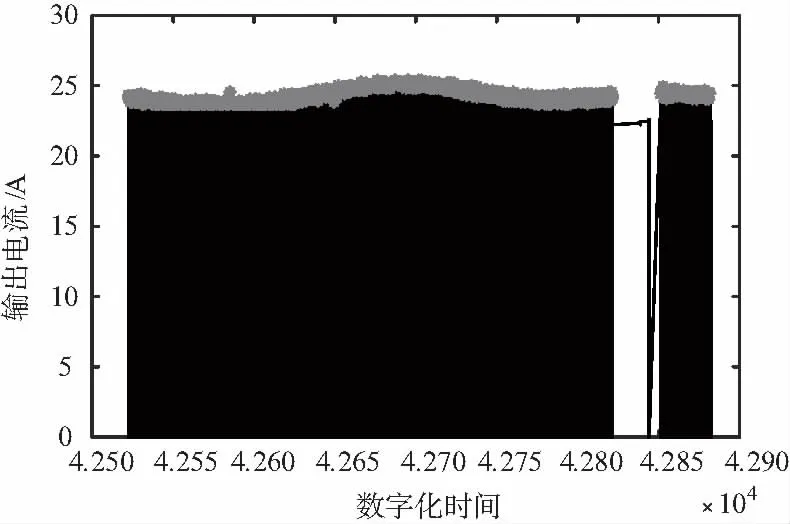
图9 二次聚类后选取的周期电流
对波峰数据使用Matlab的curve fitting进行拟合。考虑到复杂度过高会导致过拟合,因此选择五维拟合,得到太阳电池阵理论电流关于时间的函数:
y=ax5+bx4+cx3+dx2+ex+f。
太阳电池阵理论电流公式中各参数值为:a= 2.809×10-26,b= -1.495×10-20,c= 1.693×10-15,d=1.558×10-10,e= -2.147×10-5,f= 24.21,x为时间序列的数字型形式归一化后数值。
根据该函数,得到对应每个时间的供电阵电流周期理论值,与电池阵电流均值作差,得到对应每个时间的周期性补偿值。对聚类后的电流和周期性补偿值作差,就能得到消除周期性影响的电流值。而聚类后的电流值保证了温度、太阳入射角和日地距离方面的同状态,又消除了太阳光照波动、地球反照等周期性的影响,能够真实地反映太阳电池阵输出功率的衰减。
2.3.5 拟合衰减
取k=4时,得到4组数据,进行周期性补偿后,部分数据如表2所示。
表2 聚类原始数据

时间电流值时间数值化形式时间归一化处理周期性电流理论值电流均值周期补偿值去周期性电流值2016/6/1 08:42:4823.2042 522.363 0629.120 370 3624.209 3724.180.029 3723.170 632016/6/1 10:17:1123.2042 522.428 6094.664 351 8424.207 9724.180.027 9723.172 032016/6/1 10:18:5623.9442 522.429 8195.879 629 6224.207 9424.180.027 9423.912 062016/6/1 13:27:4123.6942 522.560 89226.956 018 524.205 1424.180.025 1423.664 862016/6/1 15:02:0323.4542 522.626 42292.488 425 924.203 7324.180.023 7323.426 272016/6/1 16:36:2623.0842 522.691 97358.032 407 424.202 3324.180.022 3323.057 672016/6/1 19:45:1023.0842 522.823 03489.097 222 224.199 5424.180.019 5423.060 462016/6/1 22:53:5522.9642 522.954 11620.173 611 124.196 7524.180.016 7522.943 25
以聚类后同一类点的时间为X轴,进行周期补偿后的电流值为Y轴,使用Matlab的curve fitting进行robust稳健拟合,得到结果如图10所示。

图10 对去周期补偿后的同状态点进行衰减拟合
拟合衰减时观察到聚类效果较好,同状态点输出电流下降趋势平稳,因此选择直线拟合。对聚类后的4组同状态点进行衰减拟合后,得到4组太阳电池阵输出电流与时间的关系公式,如表3拟合公式项所示。其中衰减量的计算公式为:

表3 太阳电池阵衰减评估结果
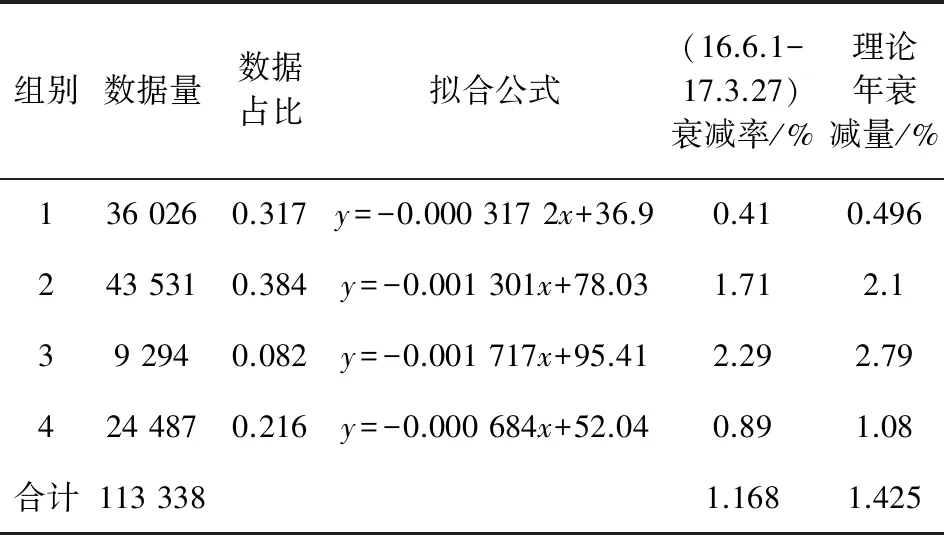
组别数据量数据占比拟合公式(16.6.1-17.3.27)衰减率/%理论年衰减量/%136 0260.317y=-0.000 317 2x+36.90.410.496243 5310.384y=-0.001 301x+78.031.712.139 2940.082y=-0.001 717x+95.412.292.79424 4870.216y=-0.000 684x+52.040.891.08合计113 3381.1681.425
得到卫星太阳电池阵年衰减率在1.425%,与文献[11,15]中的1.5%相近,符合工程设计。
4 结束语
通过以某太阳同步轨道卫星为研究对象,仅使用其单年在轨遥测数据,对该卫星太阳电池阵在轨特性进行分析和评价,使用相关度分析方法和实验,验证温度、太阳入射角和日地距离因子对太阳同步轨道卫星的电池阵影响明显。通过周期识别算法,能够识别短时间段太阳电池阵输出电流的周期性并拟合周期公式得到周期补偿量。能够利用周期补偿量弥补聚类不能完全保证同发电工况的问题,得到平稳明显的衰减趋势。最后对该卫星单年衰减估计为1.425%,符合工程设计。该基于聚类的太阳电池阵衰减估计方法对短时间段数据具有良好的处理效果,对卫星运行初期时太阳电池阵工作情况分析提供帮助,对后续进行地球静止轨道卫星太阳电池阵的设计和预测寿命时,具有一定的参考价值。
该模型仅对衰减进行估计,在后续进行太阳同步轨道太阳电池阵的寿命研究中,进一步提高功率衰减估计的精度,并根据得到的衰减估计进一步建立太阳电池阵的寿命预测模型。

