基于粒子群聚类的干扰信号分选方法
高毓泽,原浩娟,秦 琨
(上海航天电子技术研究所,上海 201109)
0 引言
面对现代雷达电子战复杂的电磁环境,雷达系统应具有更高的环境感知能力。2006年,Haykin S教授提出了认知雷达的概念[1],认知雷达因其环境感知及发射自适应处理等特点,被认为是未来雷达系统的一种发展方向[2]。从2009年开始,美军逐步将认知的概念引入电子战装备中,标志着认知电子战概念的形成[3]。认知电子战系统通过认知侦察对环境信号的实施测量、分选、特征提取和识别等信号分析处理过程。
信号分选是认知电子战系统重要的组成部分,是雷达对抗侦察系统中的关键处理过程,也是雷达对抗信息处理中的核心内容。本文针对电子侦察系统对信号分选的需要提出干扰信号分选思路,并将粒子群聚类算法用于干扰信号分选中,这对于电子侦察系统具有一定的意义。粒子群聚类算法将粒子群算法和K-means算法结合,克服了K-means算法容易陷入局部极值的缺点,保持了粒子群算法的全局寻优性,同时还具有K-means算法较快的收敛速度[4]。
1 算法原理及算法流程
1.1 K-means算法的原理及算法流程
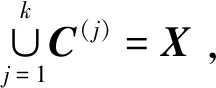
(1)

K-means算法流程如下[9]:
① 随机将数据集中的k个元素作为聚类中心;
② 计算数据集中各元素到聚类中心的欧氏距离,并且比较这些值,将元素和离它最近的聚类中心分为一类;
③ 利用式(1)计算各类的误差平均和准则函数JC;
④ 利用式(2)重新计算各聚类的中心:
(2)

1.2 粒子群算法基本原理及算法流程
粒子群(Particle Swarm Optimization,PSO)算法由Russ Eberhart和James Kennedy于1995年提出[10],算法受到鸟群觅食过程的启发。可以想象这样一个情景:鸟群中的个体随机分布在一个空间内准备觅食,食物只有一块,但是所有的鸟都不知道食物的具体位置,它们只知道自身大概离食物有多远,所以搜索离食物最近的鸟的附近区域,能有效地推断出食物的具体位置[11]。在实际优化问题中,鸟群中每只鸟所在的位置就是一个“粒子”,即优化问题的一个可能的解,鸟群的位置集合就是“粒子群”,即优化问题的“解集”。
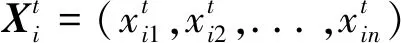
粒子的每次迭代使用式(3)和式(4)来更新其位置和速度,PSO算法的终止条件是超过了设置的最大迭代次数或者适应度值足够好。
(3)
(4)
式中,c1,c2为加速常数;rand1,rand2为服从0~1分布的随机过程;Xt+1和Vt+1为t+1次迭代中粒子的速度和位置;ω是惯性权重,它的大小决定了算法的全局搜索能力,ω越大,算法的全局搜索能力越强。开始时,算法应在全局搜索最优解,随着迭代次数的增多,算法开始收敛,应具备局部搜索的能力,因此,使用式(5)所示的线性递减权重来更新速度值。
(5)
式中,ωmin,ωmax为预先设定的最大和最小权重值;iter为当前的迭代次数;itermax为预先设置的迭代次数的最大值。
PSO算法流程如下[14]:
① 初始化粒子群,设置粒子个数m和最大迭代次数itermax;
② 初始化每个粒子的位置Xi(i=1,2,...,m)和速度Vi(i=1,2,...,m);
③ 求粒子所在位置的适应度值;
④ 每个粒子比较它在当前迭代中的适应度值和粒子目前为止搜索到的最优位置pBest的适应度值,如果当前位置的适应度值比pBest的适应度值好,则将pBest值替换为当前粒子所在的位置;
⑤ 比较粒子群中所有粒子的pBest的适应度值,将最好的适应度值所对应粒子的位置赋给gBest;
⑥ 利用式(3)~(5)更新粒子的速度和位置;
⑦ 重复步骤③~⑥,直到算法达到最大迭代次数或者适应度值足够好。
1.3 粒子群聚类算法基本原理及算法流程
PSO算法具有很好的全局搜索能力,但是当算法趋于最优解时,收敛速度就会变慢。K-means算法容易陷入局部极值点,但K-means算法有较快的局部寻优速度,所以,粒子群聚类算法具有较强的全局搜索能力,同时兼备快速收敛的优点[15]。
假设n维空间中有d个数据,p个粒子,需要聚类的个数为k,由于粒子所在的位置(n维)为粒子群算法的最优解,聚类算法的最优解为聚类中心的位置,粒子群聚类算法的最优解为k个n维的聚类中心,所以粒子群聚类算法的粒子为k×n维向量,同时粒子的速度也是k×n维向量[16],如图1所示。
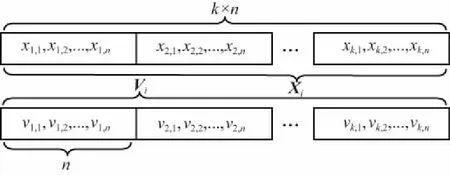
图1 粒子的位置和速度向量
(1) 初始化算法
① 给定聚类数目k,初始化粒子位置Xi(i=1,2,...,p)和速度Vi(i=1,2,...,p),编码格式如图1所示,迭代次数t根据实际需要设定。
② 粒子数p一般设为20~100,对于大部分的问题,粒子数设为50就可以得到很好的解[11]。
③ 将d个数据随机地分配为k个类,利用式(2)计算各聚类的中心mj,这k个聚类中心就组成了一个粒子,重复这一过程,直到计算出p个初始粒子(粒子位置)。
④ 将K-means算法中的误差平均和准则函数JC,如式(1)所示,作为粒子群聚类算法每个粒子的适应度函数fitness,即计算每个粒子内各聚类中所有元素与聚类中心(粒子位置)的欧氏距离之和。分别计算p个粒子的适应度函数,适应度函数值越小的粒子,聚类效果越好。
⑤ 设置每个粒子最优位置的初值pBest为第①步中初始化的每个粒子的位置Xi(i=1,2,...,p)。
⑥ 设置粒子群的最优位置gBest为第⑤步中最小适应度值对应的粒子位置。
(2) 利用式(3)~(5)产生新一代的粒子群。
(3) 根据每个粒子的新位置,按照欧式距离最小原则,将d个数据分配到最近的聚类内,更新分类结果,然后重新计算每个类的中心,得到粒子的位置。
(4) 分别计算每个粒子的适应度函数fitness,如果当前粒子的适应度函数值小于pBest所在位置的适应度函数值,则将当前粒子的位置赋给pBest。
(5) 根据所有粒子的pBest所对应的适应度值,将最小的适应度值对应的粒子所在的位置赋给gBest。
(6) 如果达到最大迭代次数,则结束算法,否则转向步骤(2);
(7) 输出分类结果和聚类中心。
2 干扰信号分选实验参数设置
2.1 干扰信号的标准化
实际的干扰信号数据比较复杂,为了消除不同量级数据之间的影响,避免大量级数据的贡献度掩盖小量级数据的贡献度,需要对原始数据进行标准化,使所有数据按比例映射到[0,1]区间之内,以相同的量级参与分类[17]。

(6)
(7)
(8)
(9)

2.2 仿真实验参数
仿真实验模拟了150个干扰脉冲,对应算法中的d个数据。这150个脉冲分别是:
① 远距离支援干扰[18]脉冲30个,采用射频噪声干扰的干扰样式。远距离支援干扰的干扰机通常置于防区外,通过施放强干扰信号掩护目标,一般采用压制式干扰的干扰样式,干扰机施放的干扰信号通常从雷达天线的副瓣进入接收机。
② 随队支援干扰脉冲45个,采用噪声卷积干扰的干扰样式。随队支援干扰是由专用的电子干扰飞机承担,干扰飞机同攻击编队一起飞行,掩护攻击编队。干扰机的干扰信号可以从雷达天线主瓣或者副瓣进入接收机,一般采用压制式干扰的干扰样式。
③ 自卫式干扰脉冲45个,采用脉冲干扰的干扰样式。自卫式干扰由攻击机携带的干扰设备施放,目的是避免攻击机遭受雷达的威胁,由于携带干扰设备的功率有限,所以一般采用欺骗式干扰,干扰信号由雷达主瓣进入接收机[19]。
④ 近距离干扰脉冲30个,采用射频噪声干扰的干扰样式。近距离干扰的干扰机和目标相对于雷达的距离和角度都不同,干扰机先于目标进入雷达,通过辐射干扰信号掩护后续的目标。主要采用压制式干扰,干扰机的干扰信号可以从雷达天线主瓣[20]或者副瓣进入接收机。
对于每个脉冲提取它的三维特征,分别是带宽、脉幅和到达角,对应算法中的n维空间,4类干扰信号的150个干扰脉冲提取出的参数如表1所示。
表1 干扰脉冲参数
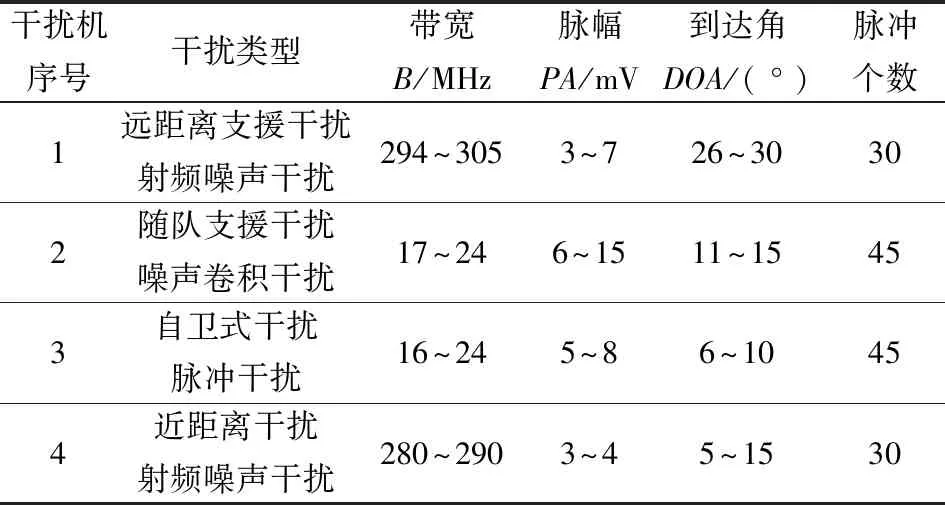
干扰机序号干扰类型带宽B/MHz脉幅PA/mV到达角DOA/(°)脉冲个数1远距离支援干扰射频噪声干扰 294~3053~726~30302随队支援干扰噪声卷积干扰17~246~1511~15453自卫式干扰脉冲干扰16~245~86~10454近距离干扰射频噪声干扰280~2903~45~1530
3 仿真结果及结果分析
3.1 干扰脉冲数据的标准化
对4部干扰机施放的4种干扰的150个脉冲数据的每一维特征值分别混合后进行标准化处理,标准化后的干扰脉冲的三维特征分布如图2(a)所示,数据有一定的交叠,图中每一个“○”都代表一个干扰脉冲,图2(b)~图2(d)为干扰脉冲归一化后的二维特征参数分布图,从图中很难分出4部干扰机的脉冲信号。

(a) 4种干扰的B-PA-DOA三维分布图
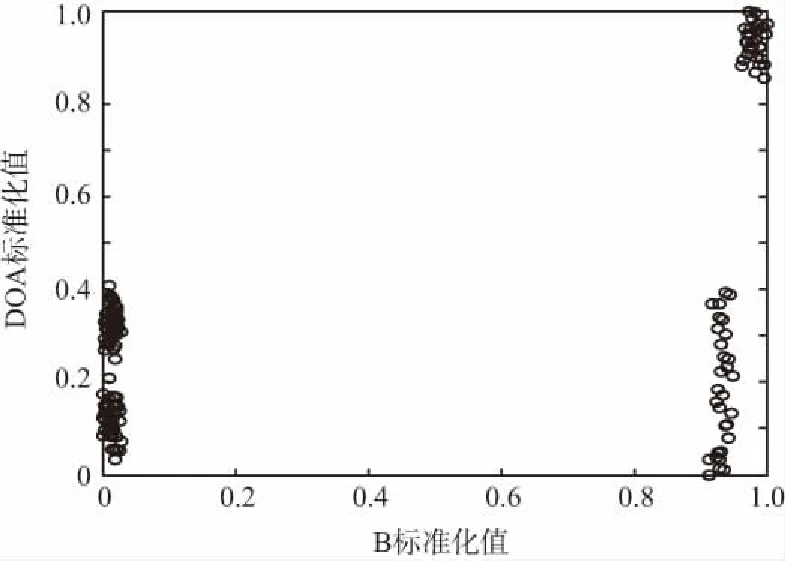
(b) 标准化的B-DOA二维分布图
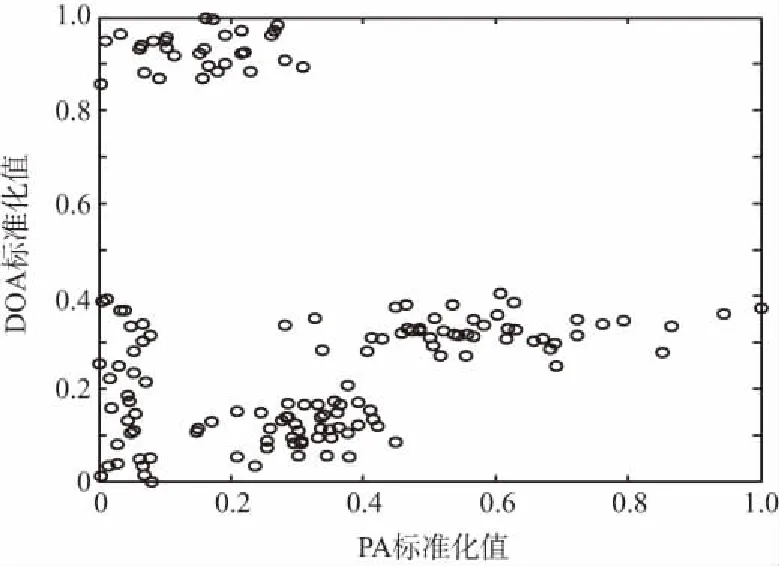
(c) 标准化的PA-DOA二维分布图

(d) 标准化的B-PA二维分布图
3.2 K-means算法对干扰信号分选
随机初始化聚类中心,选取干扰机1的4个脉冲的三维特征作为初始聚类中心,经过粒子群聚类算法后,得到聚类结果如图3(a)所示,可以看出算法将150个干扰脉冲分成了4类,但是其中有误分选的情况,将聚类结果绘制成直方图,如图3(b)所示,图中干扰机1被标记为编号2,干扰机2和3被标记为编号1,干扰机4被标记为编号3。聚类结果显示,干扰机2和干扰机3的脉冲被分为一类,所以共有90个脉冲被分选错误,算法的分选准确概率为40%。
若从4部干扰机各选取一个脉冲的三维特征作为初始聚类中心,经过粒子群聚类算法后,得到聚类结果如图3(c)所示,可以看出算法将150个干扰脉冲分成了4类,但是其中有误分选的情况,将聚类结果绘制成直方图,如图3(d)所示,图中干扰机1被标记为编号1,干扰机2被标记为编号2,干扰机3被标记为编号3,干扰机4被标记为编号4。聚类结果显示,干扰机2有4个脉冲被标记为编号3,即干扰机2有4个脉冲被分到干扰机3中,所以共有4个脉冲被分选错误,算法的分选准确概率为97.33%。
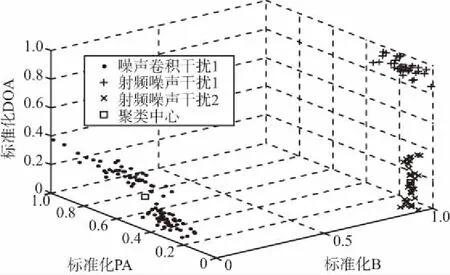
(a) 聚类效果图1

(b) 聚类统计结果直方图1
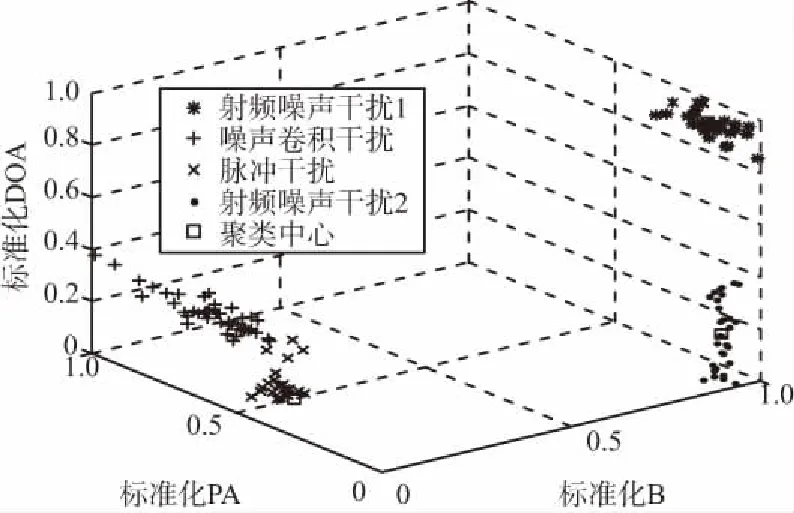
(c) 聚类效果图2

(d) 聚类统计结果直方图2
3.3 粒子群聚类算法对干扰信号分选
粒子群聚类算法分选结果如图4所示。
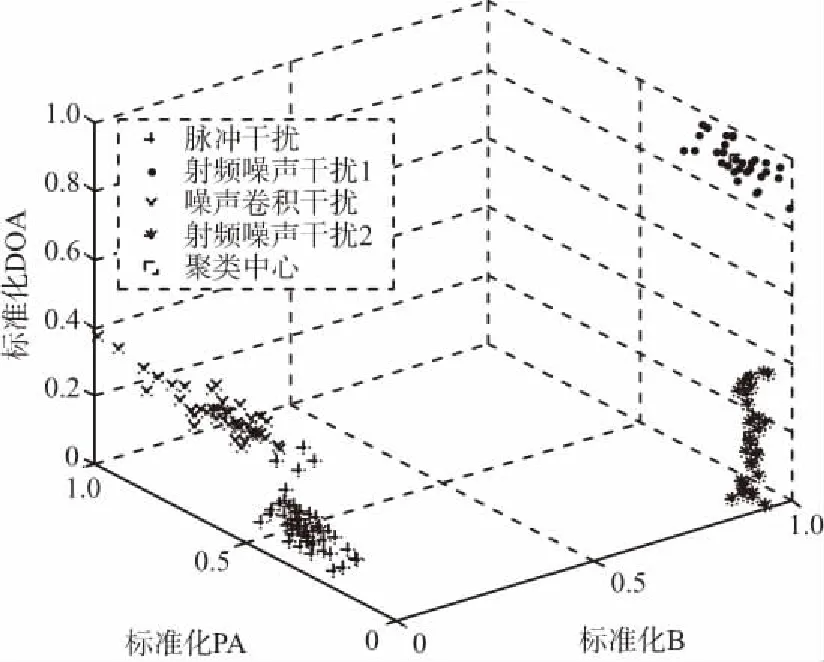
(a) 聚类效果图

(b) 聚类统计结果直方图

(c) 适应度函数收敛曲线
设置算法的迭代次数t=200,粒子数p=70,最大权重ωmax=1和最小权重ωmin=0,加速常数c1,c2都为2,经过粒子群聚类算法后,得到聚类结果如图4(a)所示,可以看出算法将150个干扰脉冲分成了4类,但是其中有误分选的情况,将聚类结果绘制成直方图,如图4(b)所示,图中干扰机1被标记为编号1,干扰机2被标记为编号3,干扰机3被标记为编号2,干扰机4被标记为编号4。聚类结果显示,干扰机2(编号3)有4个干扰脉冲被标记为编号2,即被分选为干扰机3的干扰脉冲,所以共有4个脉冲被分选错误,算法的分选准确概率为97.33%。图4(c)为适应度函数的收敛曲线,可以看出在第95次迭代时,算法已经收敛。
3.4 仿真结果分析
从以上仿真结果可以看出,K-means算法对聚类中心初值的选择比较敏感,如果初始聚类中心选择的相对集中,那么算法很容易陷入局部极值当中,得到较差的聚类效果。如果初始聚类中心选取的较为分散,例如:上述仿真中从各个类别中选取一个元素为初始聚类中心,那么K-means聚类算法的结果和粒子群聚类算法的结果一样好。这说明K-means算法初始值选取不好会导致算法收敛于局部极值点,无法得到全局最优结果,而粒子群聚类算法任意选取初始聚类中心不会影响算法结果,所以,粒子群聚类算法有很好的全局寻优能力,同时有较快的收敛速度。
4 结束语
本文介绍了粒子群聚类算法在干扰信号分选中的应用,通过分析粒子群算法和K-means算法的特点,得到粒子群聚类算法具有全局寻优和快速收敛的优点。电磁环境中对雷达影响最严重的是敌方的干扰信号,本文针对干扰信号提出干扰信号的分选,并将粒子群聚类算法应用于干扰信号分选,这对于了解战场中干扰类型和实施抗干扰手段具有一定的意义,为雷达对抗信息处理提供新的思路。实验结果表明,粒子群聚类算法能够有效地分选出干扰信号,对电子侦察系统具有较大的意义。

