面向再生制动能利用的地铁列车时刻表优化模型
刘宏杰,唐 涛,夏夕盛,陈黎洁,付瑾瑜
(1.北京交通大学 电子信息工程学院,北京 100044; 2.交控科技股份有限公司,北京 100070; 3.中国铁道科学研究院集团有限公司 标准计量研究所,北京 100081; 4.河北省实验中学, 石家庄 051430)
地铁系统因安全、舒适、方便、快捷、准点、节能等优点,已成为缓解大城市交通压力的首选方式,但是其依然消耗大量的电能[1].随着能源价格不断增长和环境保护的需要,减少地铁系统能源消耗的研究近年来已成为热点话题[2].由于列车牵引能耗在地铁系统总能耗中占比重较大[3-5],因此针对牵引能耗降低的研究成为主要方向.主要方法包括减少列车运行阻力、采用列车节能驾驶策略以及再生制动能量的利用等[1].其中,再生制动能量是指在列车制动阶段,通过再生制动系统从动能转换得到的电能.
近些年再生制动系统已经在地铁中得到广泛的应用[6].再生制动能量可以反馈到列车供电网中供牵引列车或其他用电设备使用,以减少对供电站的用电需求.再生制动能量在牵引能耗中占的比重较大,因此最大化再生制动能利用量的研究成为目前的研究热点.值得注意的是,再生制动能量必须立即被消耗掉,否则会造成电网电压的升高,危及用电设备的安全.再生制动能量的利用方式有3种[7-8],包括:可以通过能量存储设备(例如超级电容)对其进行临时存储并在需要的时候再次释放;也可以通过优化时刻表的方式对在线列车的牵引和制动进行同步,以使得再生制动能量能够立即被牵引列车所消耗;或者通过大功率电阻将其转化为热能进行消耗.能量存储设备能够大幅度提升再生制动能的利用率,同时还能够有效缓解在列车牵引或制动时电网电压的波动,但是由于其成本较高,尚未能得到普及[5].对时刻表进行优化能够在不增加硬件成本的情况下提升再生能源利用(Regenerative Energy Utilization,REU),因此成为首选方式[7].时刻表优化的基本思路是通过对时刻表的组成元素进行微调,增大列车牵引和制动时间的重叠,使再生制动能量能更多地用于其他列车的牵引,从而减少供电站的牵引用电需求.不能立即被牵引列车使用的再生制动能量通常通过电阻转换为热能,以避免电网电压的波动.
通过时刻表优化以提升REU的研究已引起广泛关注.文献[9]首次考虑REU,提出一种非线性多目标的时刻表优化模型.文献[10]针对平峰时期的时刻表优化问题,提出一种能够最大化同一供电区内列车牵引和制动重叠时间的模型,并采用商用CPLEX软件求解该问题.文献[11]利用仿真方法研究REU,并研究了发车时刻和站台预留时长的调整对REU的影响.文献[12]采用混合整数规划方法,通过优化列车发车时间来最大化REU.文献[13]提出一种列车节能操纵和时刻表调整的一体化优化方式,并设计了一种遗传算法(Genetic Algorithm, GA)来求解问题.文献[14]假设再生制动能量只能被相邻列车使用,提出一种调度规划问题来同步相邻列车的牵引和制动操作.他们采用GA求解问题,对列车间隔时间和停站时长进行了优化.文献[6]提出一种更符合实际的REU模型.在该模型中,列车进站制动时产生的再生制动能量可以被正在从该车站出发的牵引列车使用,提出一种双目标优化问题来最大化REU和最小化乘客等待时长,采用GA求解问题对列车间隔时间和停站时长进行了优化.
列车间隔时间和停站时长都是时刻表的重要组成元素,对其进行微调能够在较少或不影响乘客服务质量的前提下实现REU的提高,因此成为该类型优化问题的常用决策变量.可是,对影响地铁服务质量的首、末班车时刻在以往研究中未得到足够关注.以文献[13]和[14]为例,不同列车间的间隔时间被认为是相同的,而且其取值在优化过程中被减小.这样虽然使得在实验时间内的REU得到提高,但是对于整体地铁系统来讲,其带来的问题是日运营车次数量的增加或者运营时长的缩短.而这两个问题在实际中都是不期望的.大多既有研究对于时刻表优化问题的求解采用了简单易用的GA,并获得了比既有时刻表更好的结果,较少尝试其他优化算法来寻找更好的求解方式和结果,或者对不同算法进行对比.
本文作者在既有研究成果的基础上,提出一种新的时刻表优化模型来最大化地铁系统的REU.模型中首次考虑了日运营列车车次数量和首末班车时间均不能改变的实际约束,并采用了不同的列车间隔时间使问题具有可行解.同时,提出一种基于人工蜂群(Artificial Bee Colony,ABC)的智能优化算法来求解问题.在此基础上,基于北京地铁燕房线的实际数据进行了仿真实验,优化后的REU比既有时刻表提升了132.29%;另外,通过将基于ABC的智能优化算法与GA进行对比,证明了该算法的有效性.最后,通过对存在随机干扰情况下的REU进行仿真分析,验证了优化结果的鲁棒性.
1 时刻表优化模型
地铁系统中列车的运行路径如图1所示.每列车从始发站(站台1)出发,沿途经停所有车站,当其到达终端折返站(站台N)后列车进行折返,之后重复类似的过程直到到达终点站(站台2N-1).为方便数学建模描述,各车站按照1至N依次编号.除终端折返站N外,每个车站n含有两个位于不同方向(上行/下行)的站台,分别标记为站台n和2N-n;在不影响REU计算的前提下,终端折返站N标记为只含有一个站台N.注意车站N除包含站台N的停站过程外,还包括列车折返换端过程.连接站台n和n+1的区间标记为区段n.

图1 地铁列车运行线路示意图Fig.1 Subway train running line sketch
列车时刻表包含了各列车在各个站台的进站时间、出站时间、停站时长和列车间隔时间等.为方便计算REU,本文与文献[13, 15]保持一致,假设列车在区间按照节能驾驶方案运行,由牵引、惰行和制动三个阶段组成.该过程中相关参数如图2所示,红色点划线代表牵引阶段,黑色虚线代表惰行阶段,实线代表制动阶段.
为了计算REU,建立列车时刻表优化模型,首先需要建立各列车运行过程中各关键时刻的关系,并计算各个牵引和制动阶段的电功率.根据图2,对任意列车和任意区间,可得
(1)
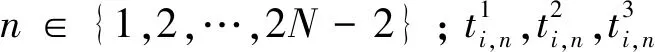
由于列车在终端折返站N进行折返,其发车时刻的计算与其他站台不同,可得
(2)
式中:xi,n为列车i在站台n的停站时长;Φ为列车在终端折返站N的折返时长.
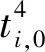
(3)

列车i的旅行时长τi由其在各区间的运行时长、各站台的停站时长和终端折返站N的折返时长决定,如下式所示
(4)
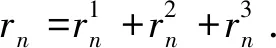
在停站过程中,列车速度为0;在区间运行过程的不同阶段,列车均按照匀加速过程运行.因此,不同时刻的列车速度vi(t)满足:
(5)
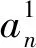
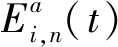
(6)
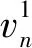
(7)
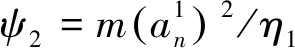
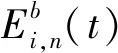
(8)
(9)
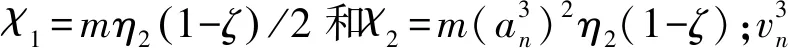

(10)
(11)
根据各列车牵引时段和制动时段的不同取值情况可得
(12)
式中:k=2N-2.
从而,根据以上变量间的关系,可以计算获得一个地铁系统中的REU.本文列车时刻表优化的目标是最大化REU,通过将列车间隔时间和停站时长作为控制变量,从安全、成本和服务质量的角度出发,考虑到首、末班车发车时间不变、列车旅行时长等约束,建立时刻表优化问题的数学模型如下:
maxE=f(H,X)
(13)
(14)
i∈{1,2,…,I},n∈{1,2,…,2N-2}
(15)
(16)
(17)
hi∈Z+,i∈{1,2,…,I-1}
(18)
xi,n∈Z+,i∈{1,2,…,I},
n∈{1,2,…,2N-2}
(19)
式中:H和X分别为列车间隔时间向量和停站时长向量,满足H=(h1,h2,…hi,…,hI-1) 和X=(X1,X2,…,Xi,…,XI).其中,对任意的i∈{1,2,…,I},有Xi=(xi,1,xi,2,…,xi,2N-2).
2 基于人工蜂群的智能优化算法
本文采用基于ABC[16-19]的算法来解决所提出的时刻表优化问题,其工作流程如图3所示.
为了降低ABC算法陷入局部最优解的机率,在ABC算法迭代M2次收敛于一个近似最优解后,算法会进行重启,并重新开始搜索.

图3 基于ABC的优化算法流程图Fig.3 Procedure of ABC-based optimized algorithm
在每次优化迭代过程中,利用ABC算法的机制更新前nb个解,并利用第nb+1个解保存上次迭代过程中找到的最好结果,从而防止优化过程中解的质量变差.其中,nb为整体蜂群中蜜蜂的数量,包括ne个引领蜂、no个跟随蜂和ns个侦察蜂,即nb=ne+no+ns.
对于引领蜂和跟随蜂,其优化过程是在之前某一个解的基础上,利用局部搜索算子生成一个新解.为了保证新解的多样性,局部搜索算子每次按照ps,pi,pm和pc的概率从交换、插入、变异和交叉四个算子中随机选择一个.引领蜂和跟随蜂工作机理的区别是,前者依次从之前获得的较好解中找到一个作为其工作基础,而后者则每次在这些较好解中采用轮盘赌的方式找到一个解作为其工作基础.
侦察蜂则总是通过随机方式生成各个新解,以保证算法的全局搜索能力.
为提高算法收敛速度,每次生成的新解需要检查其可行性,并对不能同时满足约束式(14)~式(17)的解立即进行修复,从而减少不必要的计算量.
3 实验结果和分析
3.1 试验参数和结果
本节基于北京地铁燕房线的数据进行了仿真实验,并将基于ABC的算法与GA进行了对比.燕房线共有9个车站,按照本文所述模型,共有17个站台和16个区间.列车在各站台的停站时长和各区间的运行时长如表1所示.其中:DEP为出发站台编号;ARV为到达站台编号.注意列车运行到站台2N-1后会结束其旅行,因此不需要关注在该站台的停站时长.另外,既有时刻表中,不同列车在同一站台的停站时长相同,在同一区间的运行时长也相同,且各相邻列车的间隔时间也一致.列车间隔时间和其他相关的参数如表2所示.为了跟既有时刻表保持一致,本文实验过程中各列车的停站时长也保持一致.即:对于所有的n∈{1,2,...,2N-2},满足xi,n=xj,n, ∀i,j∈{1,2,...,I}.
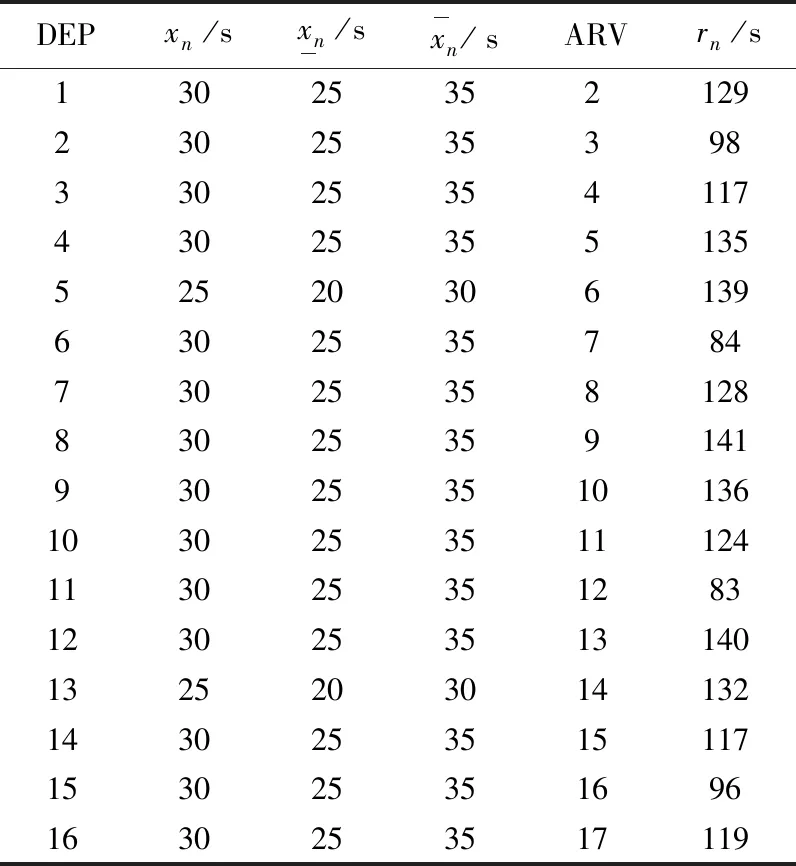
表1 站台停站时长和区间运行时长
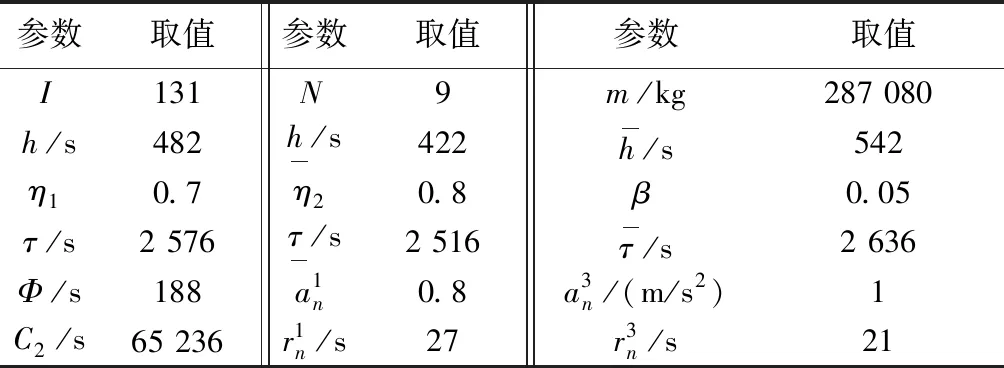
表2 燕房线的其他参数
由于本文时刻表优化模型的非线性和复杂性,难以通过商用软件(如CPLEX)在可接受的时间内获得精确解.为了验证算法的有效性,分别采用本文所提出的基于ABC的算法和GA[6, 14]算法对该时刻表优化问题进行了求解.基于ABC的算法中,引领蜂、跟随蜂和侦察蜂的数量分别设置为10、10和20(蜂群整体的数量为40);每次优化迭代50代后算法重启,重启3次(总共运行4次,总迭代次数为200);交换、插入、变异和交叉算子的选择概率分别为0.1、0.1、0.2和0.6.为了保证两种算法对比的公平性,设置GA的种群为40,最大迭代次数为200,GA算法采用变异和交叉算子,且两者的概率分别为0.2和0.8.
两种算法分别仿真运行了5次,所获得的优化结果对比如表 3所示.其中:REUABC为基于ABC的算法优化后的REU;REUGA为GA优化后的REU;IRABC为REUABC相对于既有时刻表的增长率;IRGA为REUGA相对于既有时刻表的增长率.同时,将既有时刻表代入到模型中,可得其对应的REU为18.38 kJ/kg.可见,两种算法都能够用于时刻表优化求解,并能够比既有时刻表大幅提升REU.同时,无论是所获得的最好值还是平均值,基于ABC的算法所获得的解的质量均优于GA.
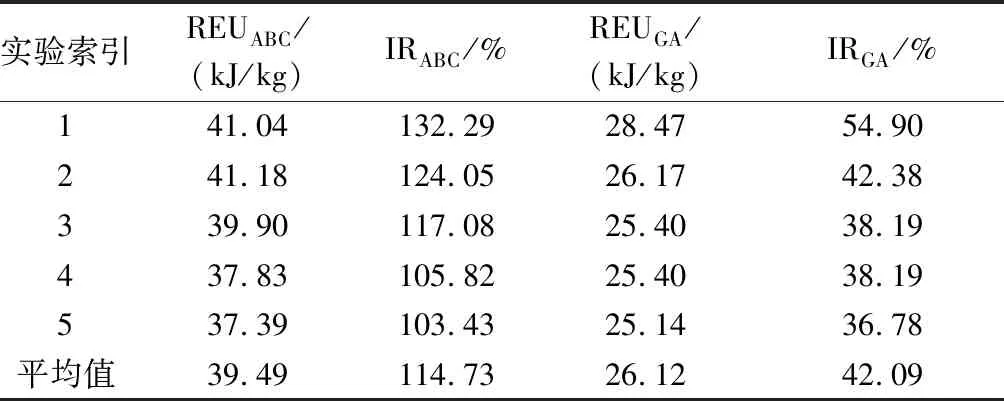
表3 再生制动能利用量优化结果对比
图4给出了基于ABC的算法在获得最优解时的收敛过程.可见算法在迭代过程中能够迅速收敛到一个近似最优解,并在之后不断的对其改进.
图5给出了所获得的优化时刻表和既有时刻表的对比.为了将其与既有时刻表的差别展示的更清楚,图5(a)为优化后的时刻表中各列车间隔时间与既有时刻表中的差值,图5(b)显示了优化后的时刻表中和既有时刻表中的停站时长.可见大多数间隔时间和停站时长的改变幅度都很小(远小于规定的调整门限).通过对时刻表较小的调整,可以在对乘客服务质量影响较小(列车间隔时间和停站时长的改变都很小,旅行时长满足准点性要求,首/末班车投入服务的时间均不变)的前提下,使REU得到大幅度的提升(相对于既有时刻表,最佳优化结果的REU增长率达到132.29%,5次优化结果的平均增长率达到114.73%).

图4 基于ABC的算法收敛过程Fig.4 Convergence process of ABC-based algorithm
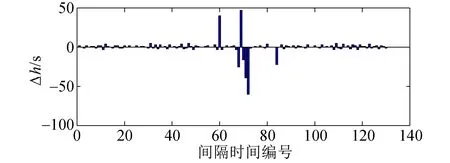
(a)优化前后列车间隔时间变化
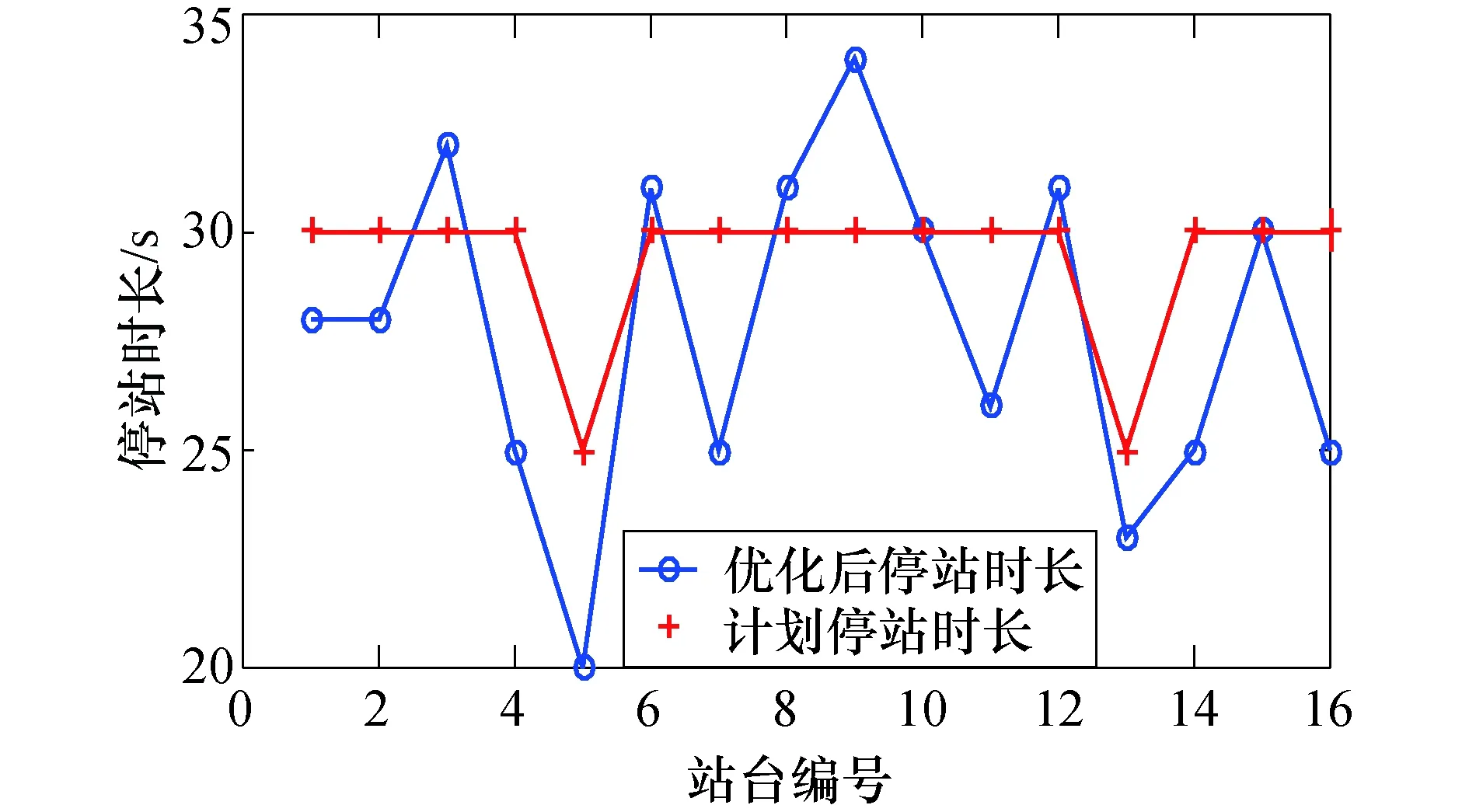
(b)优化前后停站时长对比图5 优化时刻表和既有时刻表的对比Fig.5 Optimized timetable vs. current one
3.2 优化时刻表的鲁棒性
在干扰情况下的鲁棒性是通过时刻表优化提高REU的方法所面临的最大问题[20],而小幅度的实时干扰在地铁系统中是难以避免的[21].因此,对优化时刻表在不同幅度干扰情况下的REU进行了仿真分析.实验过程中,本文对每一个决策变量(即间隔时间和停站时长)均施加了一定程度的随机干扰.随机干扰的取值方式是在{-δ,0,δ}中随机取一个值.δ取不同数值时的实验结果如表 4所示.其中:REUδ为 存在干扰δ时的REU.每一组实验均进行了100次,表4中展示的为其平均值.增长率是指优化后时刻表在干扰情况下的REU相对于既有时刻表中REU的增长率.
注意δ=0表示不存在干扰时的情况.可见,随着干扰幅度的加大,优化时刻表的REU逐步降低.但是,即使受到3s干扰的情况下,其REU仍比既有时刻表提高了70.67%.因此,优化时刻表具有一定的鲁棒性,无论在正常情况下还是存在干扰时,均能够实现一定程度的节能.

表4 干扰情况下的再生制动能利用量
4 结论
本文在考虑地铁系统首、末班车服务时刻不变和列车运行准点性等实际约束的前提下,通过优化时刻表来提升再生制动能利用量.通过设计基于ABC的智能优化算法并基于燕房线的数据对问题进行仿真求解,使优化结果比既有时刻表提升了132.29%.另外,通过与GA对比,证明了该算法的有效性.通过施加随机干扰,验证了优化结果的鲁棒性.
为了进一步实现地铁系统的节能运行,下一步计划结合时刻表优化方法和安装能量储存装置的方式,研究合理的配置方法,进一步提升REU;同时,计划研究列车运行调整方法,使列车受到干扰时能够尽快恢复到计划时刻表,减少不必要的能量浪费.

