斜流中螺旋桨的水动力性能研究*

胡 洋 胡 健 刘亚彬

(中国船舶重工集团公司第七一三研究1) 郑州 450015) (哈尔滨工程大学船舶工程学院2) 哈尔滨 150001)

0 引 言

在进行螺旋桨的设计和性能预报时，通常考虑其在轴向流中的水动力性能.然而，在螺旋桨使用寿命期间，由于船尾复杂的流场、船舶处于纵倾状态、螺旋桨与方向舵相互作用等原因，桨轴方向可能与来流存在夹角，另外，高速艇设计时，主机轴线往往向下倾斜，加上航行纵倾的影响，致使螺旋桨处于斜流中工作.相比于设计工况，斜流中螺旋桨表面载荷加重，这对桨性能及结构都有不利影响.当流体以一定入射角流入桨盘面时，由于螺旋桨自身的旋转以及桨叶结构的影响，桨叶上流体流入速度分布不均匀，桨叶上水动力载荷呈现明显的非定常性.

孟庆津[1]对阿·姆·巴辛所著《螺旋桨原理与计算》一书中第56节进行翻译与改写，给出了表征斜流对螺旋桨工作影响的相关公式.张志荣等[2]采用准定常、滑移网格和动网格三种处理方法计算了斜流中螺旋桨水动力性能，得到后两种方法均能得到准确计算结果的结论.张文照等[3]计算了斜流中艇后螺旋桨的水动力性能，计算结果表明随着攻角增大，艇后螺旋桨推力先减小后增大.Krasilnikov等[4]用RANS方法计算了斜流中螺旋桨非定常水动力性能，通过实验对比验证了计算的准确性.Gaggero等[5]通过RANS方法与面元法分别计算了斜流中螺旋桨非定常水动力性能，结果表明RANS方法更加接近实验结果.Dubbioso等[6]使用CFD软件分析斜流入射角为10°～50°对螺旋桨性能的影响，计算结果表明斜流角度会使桨叶上轴向载荷的峰值位置发生偏移.常欣等[7]分析了斜流中螺旋桨的水动力性能，得到桨叶表面压力分布不均匀，是激振力产生的根本原因的结论.

文中以DTMB4679桨为研究对象，通过CFD软件建立数值水池模型，首先计算了设计工况下螺旋桨的定常水动力性能，得到该桨的敞水性征曲线，然后计算了斜流中螺旋桨的非定常水动力性能，分析了单个桨叶上载荷与斜流角度的关系.

1 数值方法

忽略水的可压缩性，流体运动需满足连续性方程及动量方程.RANS方法基于雷诺时均原理，将瞬态Navier-Stokes方程中变量分解成变量和时均常量，从而把流动的变量嵌入连续性方程及动量方程，并在一定的时间间隔内去平均，得到雷诺平均N-S方程为

(1)

(2)

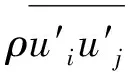
表征螺旋桨水动力性能的主要参数见式(3)，其中kti，kqi为类比于推力系数和转矩系数定义的不同方向上力与力矩系数：

(3)

式中：i=x，y，z为坐标轴正方向.

2 计算模型

计算所选用的模型是DTMB 4679桨.参照文献[8]，该桨几何参数见表1.

表1 P4679桨主要参数

将桨置于一个直径为1.2D的圆柱体旋转域中，计算域使用9D×5D×5D的长方体，其左端流体入口处距桨中心点的距离为4D，见图1，图中左端边与底面为流体入口面，右端面与底面为流体出口面.

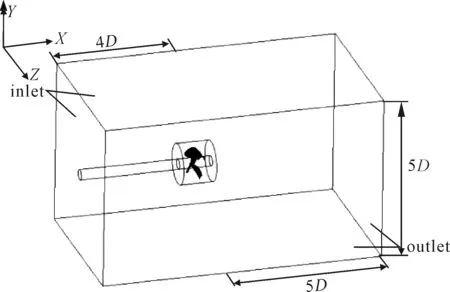
图1 计算域模型

在ICEM中将建好的模型进行结构化网格划分，见图2～3，然后导入Fluent软件进行数值计算.计算采用SIMPLEC算法，湍流模型选择k-ωSST模型.流体入口面设置为velocity-inlet，出口设置为pressure-outlet，其余面则设置为symmetry.计算时给定桨转速为492 r/min.

图2 桨叶上网格

图3 流体域的网格划分

3 轴向流中螺旋桨的定常水动力性能计算

设计工况下，流体沿螺旋桨轴向流入桨盘面，桨叶表面压力不随时间变化，呈现定常特性，图4为计算得到的P4679桨敞水性征曲线.

图4 敞水性征曲线

进速系数J=1.078，螺旋桨转速n=8.2 r/s时，计算得到单个桨叶上r/R=0.7，r/R=0.9半径处叶剖面上压力分布，并与实验值的对比，见图5.由图5可见，计算结果与实验值基本吻合，只有在导边(X/C=0)附近计算结果与实验稍有差异.对比结果表明计算可信度高，反映出敞水性征曲线的准确性.桨叶上压力分布均匀，梯度小，也符合大侧斜桨良好空泡性能的特性.

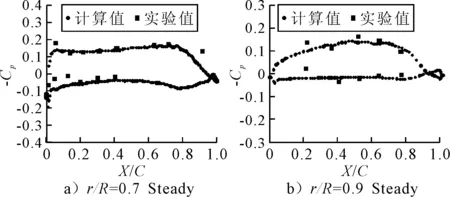
图5 定常压力系数分布(J=1.078)

4 斜流中螺旋桨的非定常水动力性能分析

当来流方向与桨轴间有夹角α时，桨叶上不仅仅产生轴向载荷，还会有横向和垂向载荷，这些载荷会随着螺旋桨旋转呈周期性变化，这一方面会影响螺旋桨的推进性能，一方面又会对轴系结构有不利影响.

4.1 桨叶表面水动力载荷分析分析

图6为斜流角度示意图，由图6可知，来流速度U与螺旋桨轴向夹角为α，在X，Y轴正向上分量分为Ucosα和-Usinα.初始时刻，blade1的中心线与Y轴正方向重合，见图7，若将迎着来流方向的位置定义为0°，叶片的中心线与Y轴正向的夹角θ即可表示该叶片的位置，初始时刻， 三个叶片分别在0°，120°，240°位置处.

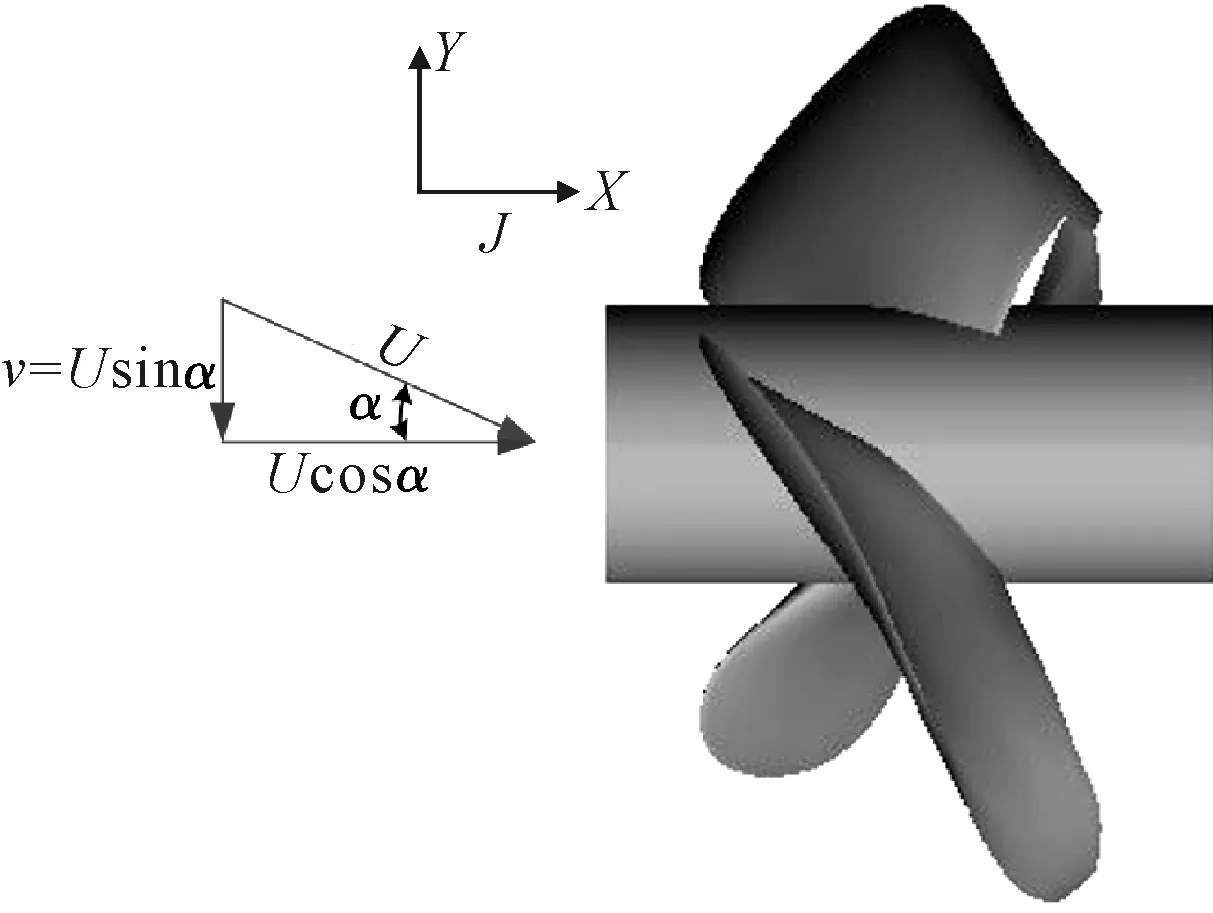
图6 斜流角度示意图

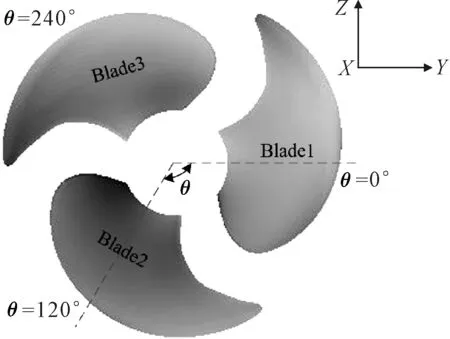
图7 初始时刻桨叶位置

为了分析斜流中桨叶表面水动力载荷分布，也为后文数值计算结果提供理论依据，图8a)分析了桨叶上流体流入情况.将坐标系定义在桨叶上，把流体速度投影到叶片上，得到轴向速度分量和周向速度分量分别为

uaxial=Ucosα

(4)

utangential=Ωr-Usinαsinθ

(5)

式中：r为叶片径向位置；Ωr为桨叶旋转引起的相对周向速度，Ωr=-ωr.

根据几何关系，可以给出叶剖面上流体的几何迎角为

(6)

式中：Θp为叶剖面处的几何螺距角.

由式(4)～(5)可知，轴向速度uaxial及螺旋桨旋转产生的周向分量Ωr是恒定的，而桨叶上周向流体速度与斜流横向分量有关的项Usinαsinθ随叶片位置θ变化，根据式(6)可知，叶剖面上流体迎角β也会周期性变化，这是桨叶表面产生周期性变化载荷的根本原因.

在纯轴向流(α=0°)中，桨叶上流体周向速度分量恒为Ωr，故螺旋桨旋转过程中叶剖面上经历了恒定的流体迎角β.而斜流中，桨叶位置从θ=0°开始，周向流体速度分量遵循正弦变化，极小值在θ=90°位置处，极大值在θ=270°位置处；迎角β也随之变化，并在对应位置上出现极值.为了分析桨叶表面流体周向速度分量与迎角β的关系，图8b)～c)给出了叶片2、叶片3上叶剖面流体速度多角形，叶片2位置处Usinαsinθ与Ωr方向相反，导致桨叶表面周向速度分量减小，相对于纯轴向流中，迎角β减小.而叶片3上Usinαsinθ与Ωr方向相同，相对于纯轴向流中，迎角β增加.

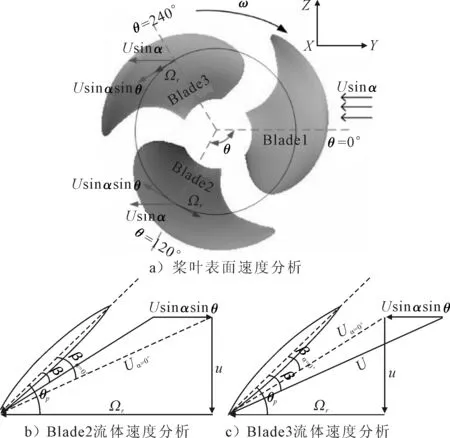
图8 叶剖面上流体速度多角形

根据以上分析，桨叶表面流体不均匀的流入，导致旋转过程中叶片上载荷分布不均匀，这是桨叶上产生周期性变化的力和力矩的根本原因.

4.2 计算结果验证

4.2.1推力和转矩系数的验证

图9为斜流角度α=7.5°时单个叶片推力和转矩系数的变化规律，本文计算值与MARINTEK(挪威海洋工程研究中心)的面元法程序计算结果十分接近[9]，文献[10]的RANS方法计算结果虽然在数值大小上与其他结果差别不大，但极值位置偏移理论位置比较明显，可能是非结构网格对极值位置的捕捉不够精确.根据计算结果可以看出，在螺旋桨旋转1周过程中，从0°位置开始，推力与转矩随着旋转角度的增加而逐渐减小，在π/2位置附近达到极小值，之后开始增大，在3π/2位置附近达到极大值.

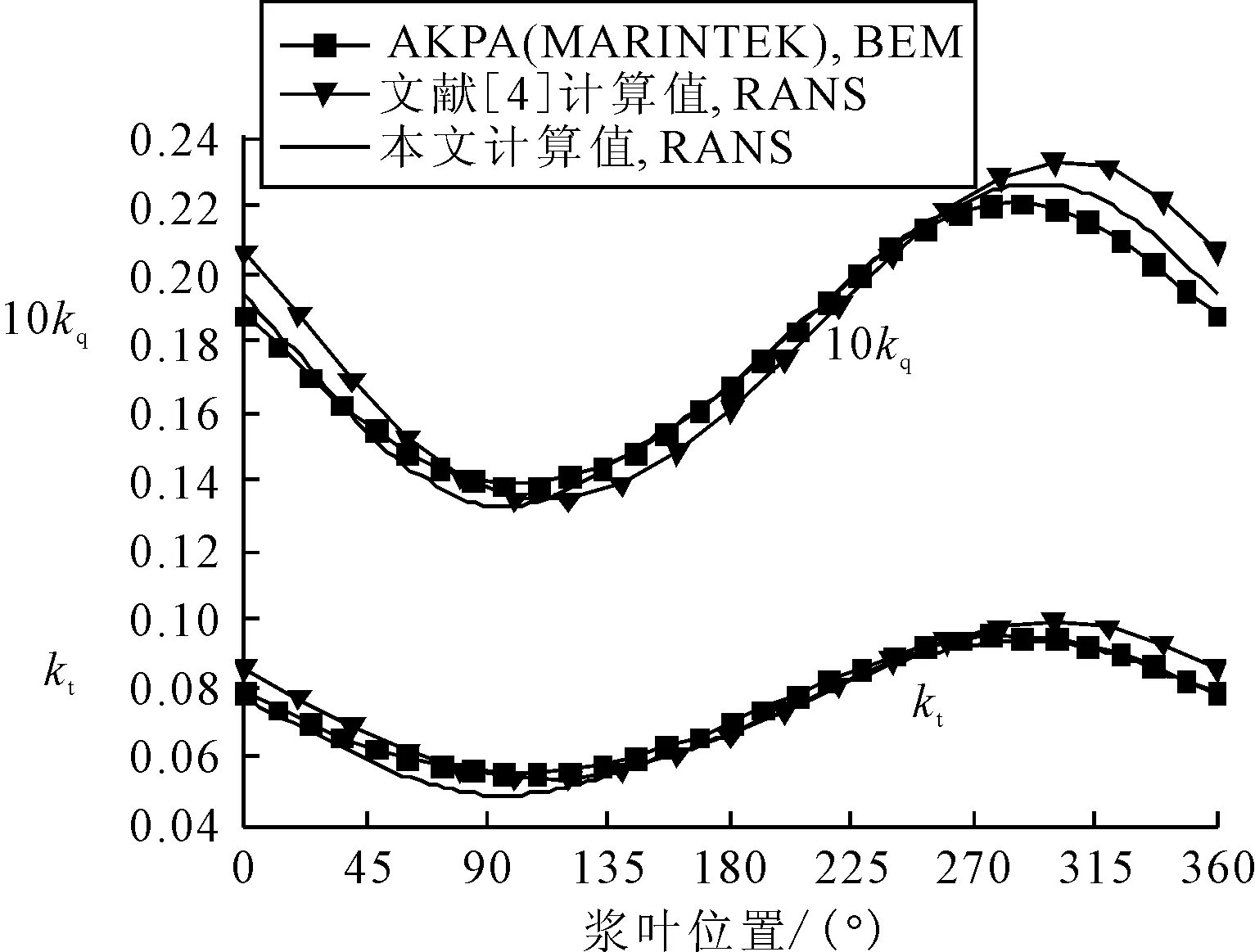
图9 推力系数与转矩系数对比验证，J=1.078，α=7.5°

4.2.2非定常压力分布的验证

图10～11为进速系数为J=0.719，1.078时桨叶上r/R=0.7，0.9叶剖面上压力系数分布，并和实验值作了对比，计算结果与实验值吻合较好，导边(X/C=0)附近、叶梢(r/R=0.9)等位置处与实验值有一定差异，但都在误差允许范围内.由图10～11可知，J=0.719时的计算结果更接近于实验值，对于相同的螺旋桨转速条件下，J=1.078对应更大来流速度，要想得到同样精确度的计算结果则需要更精细的网格及更小的时间步长.此外，r/R=0.7半径处叶剖面的计算结果优于r/R=0.9处，其原因是r/R=0.9处叶剖面靠近叶梢，一方面叶梢附近形状更加不规则，网格精度低于桨叶中部，另一方面叶梢附近载荷受尾流影响更大.

图10 压力系数分布,r/R=0.7

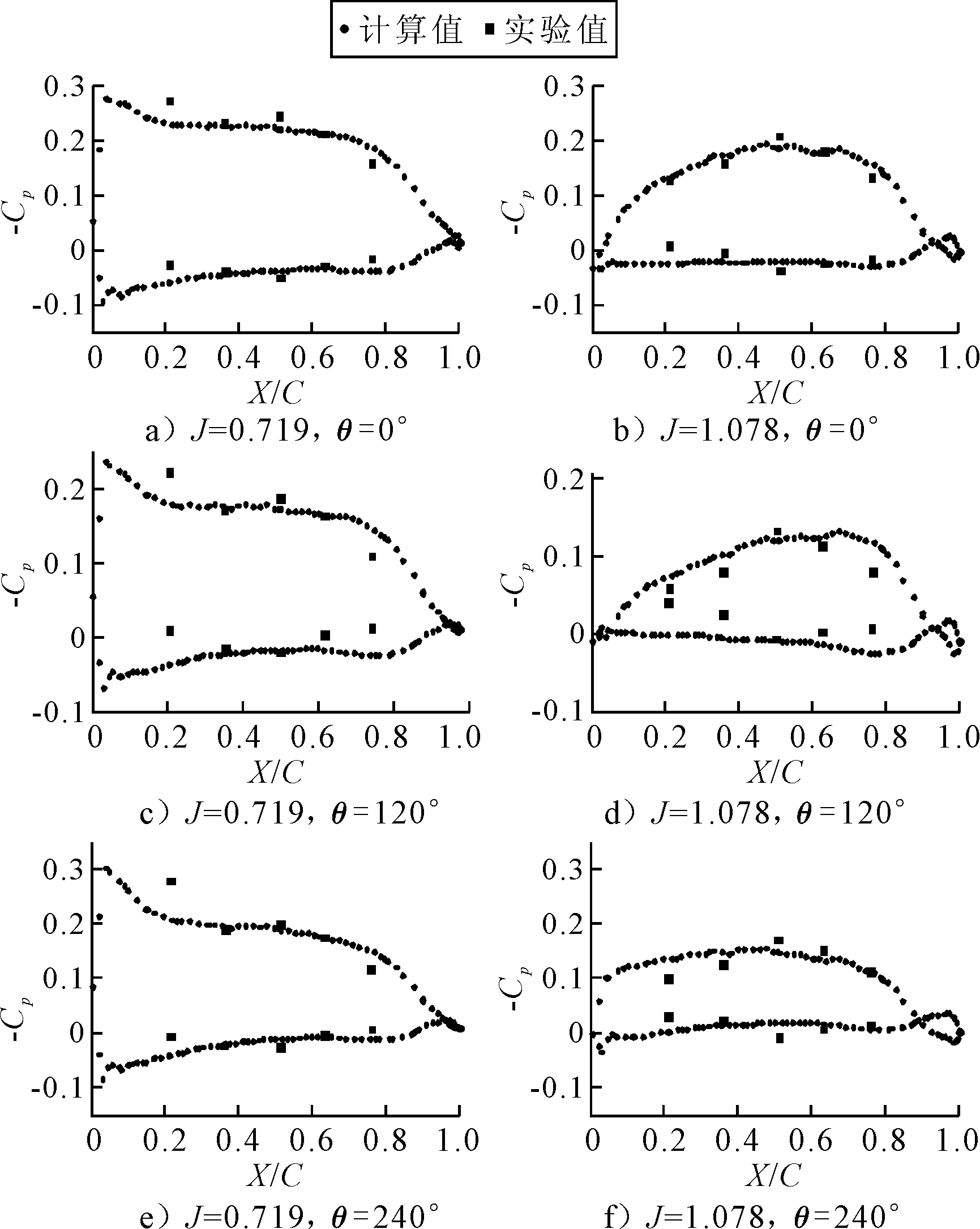
图11 压力系数分布,r/R=0.9

4.3 单个桨叶上载荷分析

图12～13为不同入射角(α=7.5°～60°)的斜流中，螺旋桨旋转1周时单个桨叶上力和力矩系数的变化情况.桨叶上载荷随桨叶位置变化而近似呈正弦变化，这种变化趋势反映出了桨叶上流体实际流入情况，与前文中桨叶表面水动力分析结果相符.由图12～13可知，在桨盘面下半部分位置区域(0°<θ<180°)，叶片上推力系数ktx与横向力系数kty普遍较小(绝对值)，相比而言，垂向力系数ktz的小应力区域有π/2的偏移，集中在180°<θ<360°区域.力矩与力有着同样的分布规律.

随着斜流角度α的增加，三个方向力系数的峰值都近似呈线性增加趋势，谷值在α较小时也线性减小.推力系数峰值位置会随着α的增大而向θ较大的位置偏移，这主要是受尾流的影响，由于螺旋桨的搅扰，流出桨盘面的流体速度大小与方向较流入的流体有所不同，并有一定的回转运动.计算结果也与文献[11]中计算得到的偏移趋势一致.

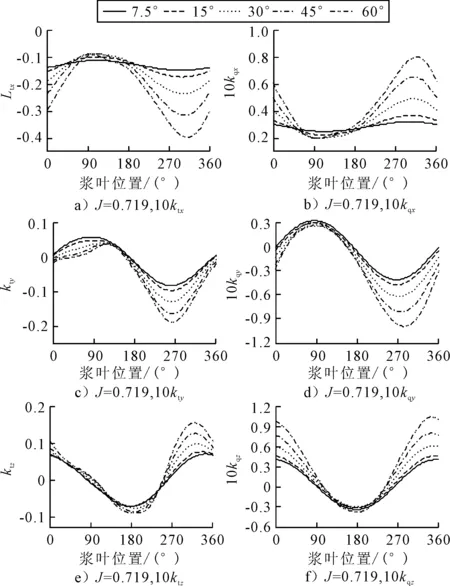
图12 单个桨叶上力(左)与力矩(右)系数，J=0.719

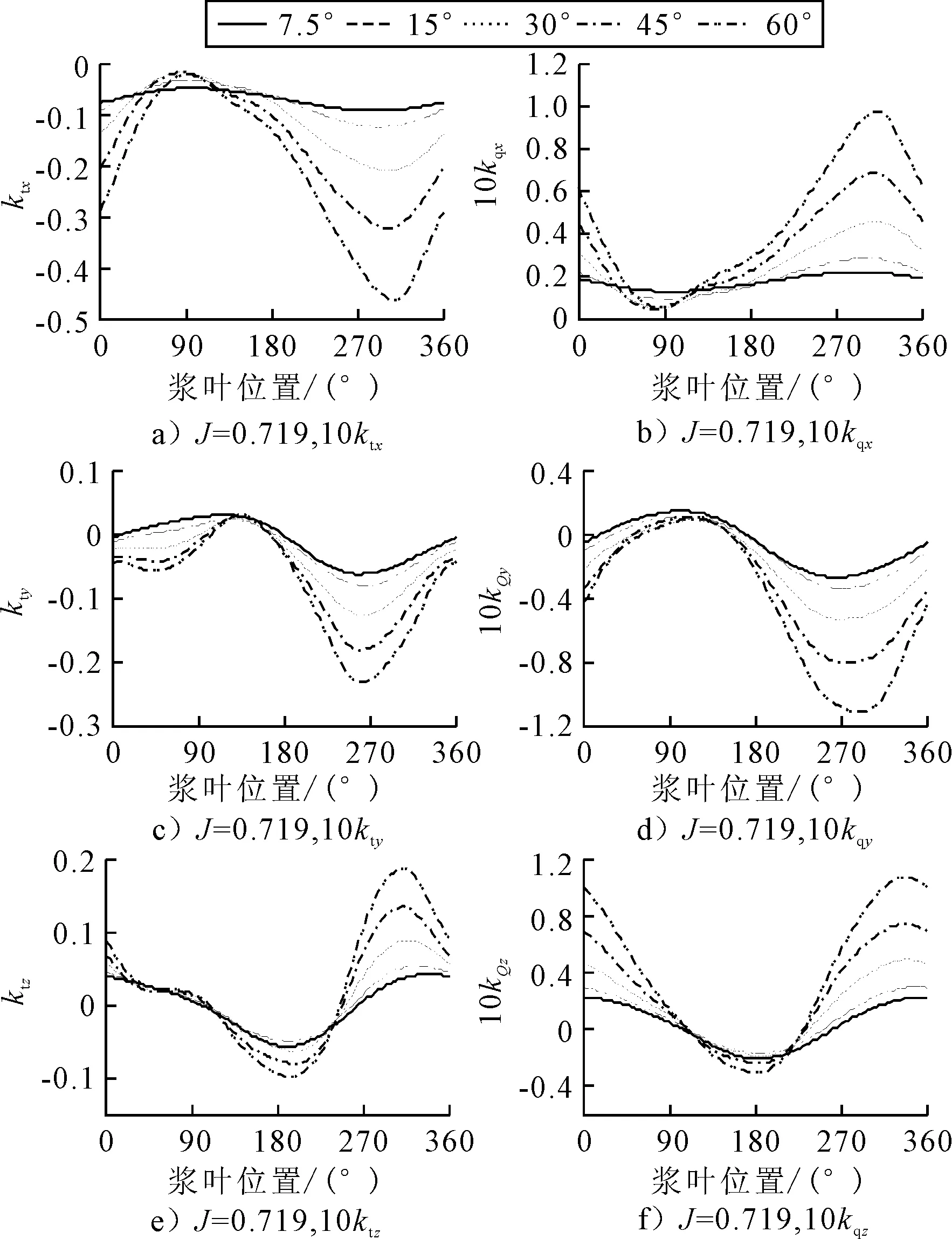
图13 单个桨叶上力与力矩系数，J=1.078

将图12、13中单个桨叶在一个旋转周期内的力与力矩系数取平均值见表2～3，由表2～3可知，斜流角度α从0°增大到30°，J=0.719与J=1.078工况下ktx分别增加了22%与56%，可见J越大ktx随α增大而增长的越快，在极大斜流入射角(α=60°)工况下，J=1.078时桨叶上轴向载荷已经接近于J=0.719时.

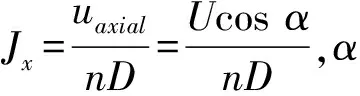
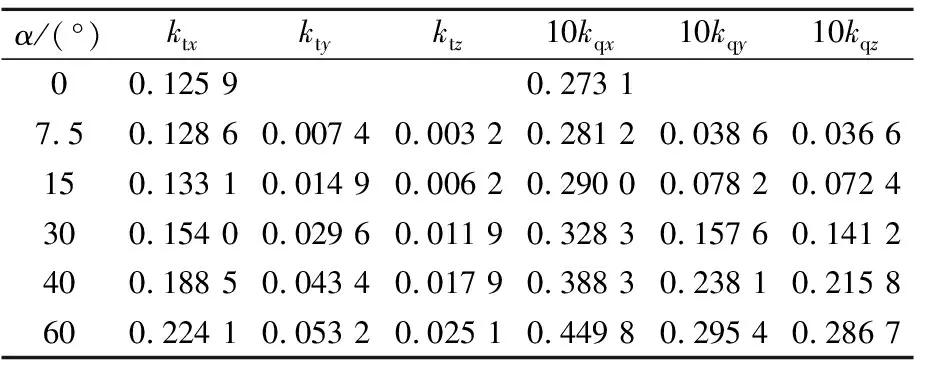
表2 桨叶上平均载荷，J=0.719

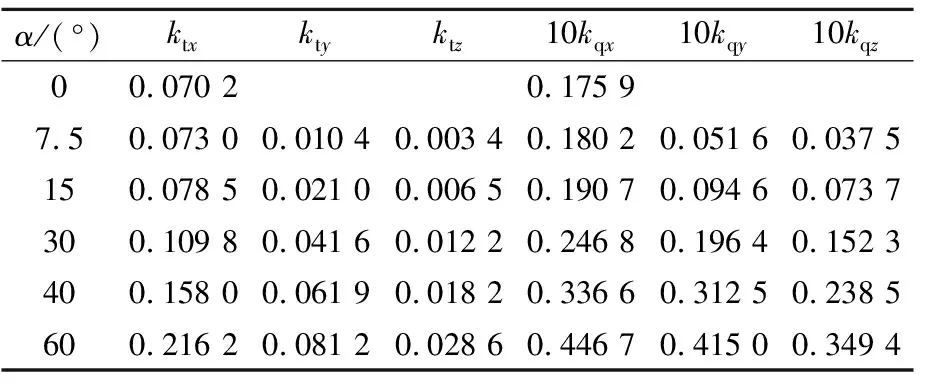
表3 桨叶上平均载荷，J=1.078

图14 桨叶上载荷系数与来流入射角之间的关系

为了更清楚的描述桨叶上的载荷情况，图15给出了侧向(包括横向、垂向)载荷占轴向载荷系数的比重.我们知道，轴向推力系数ktx对螺旋桨的推进性能起直接作用，而横向力kty与垂向力ktz对轴系结构十分不利.从图中可以看出，进速系数J越大，侧向载荷占推力的比重越大，斜流对螺旋桨的性能与结构影响越不利.螺旋桨进速系数分别为J=0.719、 1.078时，横向力系数kty占推力ktx的比重最大分别能达到24%与39%，而垂向系数力ktz占ktx的比重最大只有11%与13%，可见侧向力主要集中在有流体速度分量的方向上.此外，侧向的力矩系数占轴向力矩系数的比重很大，J=1.078时横向与垂向最大力矩系数的大小可接近轴向力矩系数.

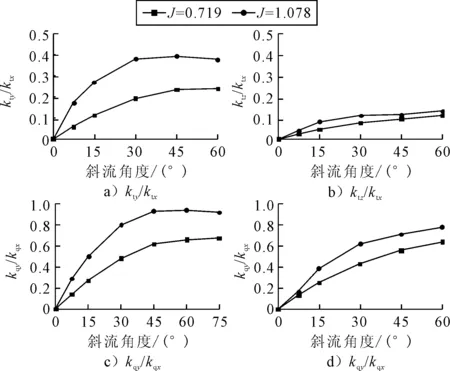
图15 侧向载荷占轴向载荷系数的比重

图16为螺旋桨效率曲线，斜流入射角增大时，高进速下螺旋桨推进效率ηo增长更快.其原因可能是高进速时压力载荷(与推力ktx有关)比粘性载荷(与转矩kqx有关)增长更快，再由式(3)可知,高进速时螺旋桨效率随斜流角度的增加而增长较快.根据计算数据可验证上述猜想是正确的，见表4，ktx(↑)、kqx(↑)表示斜流中桨叶上轴向载荷系数较纯轴向流中的增量，J=0.719时，ktx与kqx的增量比较接近，而J=1.078时ktx增长明显快于kqx.

图16 效率曲线

Jα/(°)7.5153045600.719ktx(↑)/ %2.25.722.447.478.0kqx(↑) / %3.06.220.242.264.71.078ktx(↑) / %4.011.956.4125208kqx(↑) / %2.58.440.391.4154

图17为J=0.719时桨叶上压力云图，以便更好的了解斜流条件下桨叶上压力分布.由图17可知，桨叶上迎流区域载荷较大，在大斜流角度工况中，桨叶上压力分布的非均匀性表现的更加明显.迎流的θ=0°位置处桨叶靠近叶梢位置及θ=240°位置桨叶的导边上压力变化梯度较大，而顺流旋转的θ=120°位置处桨叶的压力面与吸力面上的压力分布比较均匀.

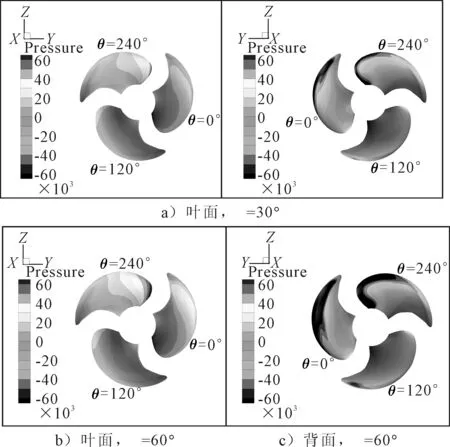
图17 压力云图，J=0.719

5 结 论

1) 斜流中桨叶上流体不均匀的流入，桨叶上流体周向速度分布不均匀，是桨叶上非定常载荷产生的根本原因.

2) 桨叶上不同方向上载荷均随斜流角度增加而近乎呈线性增加趋势，并且在大进速工况中，增长速度更快.

3) 桨叶旋转过程中，产生较大推力的位置集中在桨盘面上半部分区域(0°<θ<180°)，较小推力的位置则集中在桨盘面下半部分区域(180°<θ<360°)，但极值位置随着入射角的变化而出现小幅度偏移.

4) 斜流角度增加时，高进速工况下压力载荷比粘性载荷增长更快，螺旋桨效率也较低进速工况下增长更快.