国际奥数竞赛较量背后

周甜

早上八点，一间可容纳上百人的阶梯教室里，60名入选奥数国家集训队的队员与34名全国各地的旁听生早已落座。讲台上，老师挥动着笔，思路凌厉，台下的“最强大脑”们飞速运转，一个个见招拆招、化繁为简的奇迹时刻随之诞生。

对于对奥数无感的人来说，这样的课听得让人不知所云，跟不上节奏，对于痴迷者而言，这是一场又一场探索未知的奇妙之旅。

这里是广州华南师范大学附属中学，是中国盛产奥数金牌学霸的重镇之一。3月3日起，第60届国际数学奥林匹克（IMO）中国国家集训队的选拔在此展开。9天时间里，60名候选人要历经两轮、4个半天、每次长达4.5小时的“超长版”考试，其中16人晋级下一轮。3月底，将有6人勝出组成国家队，7月赴英国巴斯参赛。

中国的数学竞赛之路已走过半个多世纪，参加IMO竞赛也有三十余年。其间，成绩曾长达十余年雄踞IMO首位，但近几年，却连续四次与团体冠军失之交臂。今年2月底，罗马尼亚大师杯数学竞赛团体第6名的成绩更是把中国的奥数推上了风口浪尖。

前世今生

华南师大附中的数学老师陈嘉华有多重身份：他既是学校专门开设的奥林匹克班的数学教练，也是首次入选奥数国家集训队的中学组教练，他的一名高一弟子今年还进入了国家集训队。此外，他也曾是华南师大附中奥班的学生。

陈嘉华和奥数的结缘是在小学五年级。1999年，广州市小学数学奥林匹克业余学校面向社会招生，听闻消息的他感到好奇，和小伙伴一起报了名。在这之前，他小学数学的成绩不错，但对什么是奥数没有概念。通过奥校考试后，他开始每周末抽出半天时间去上课，学的内容也是如今大家听起来很熟悉的行程问题、鸡兔同笼等。他回忆，当年的奥数班还只是基于小学内容的拓展和延伸，没有超前学习，在他眼中，“纯粹就是兴趣班”。小学六年级，他还参加了颇具名气的“华罗庚金杯”少年数学邀请赛，拿了广州市一等奖。

顺着兴趣的指引，接下来，他考上了华南师大附中的初中奥赛班，初三学完了高中的所有知识，之后，又升入高中奥班，并在高二、高三接连两年获得了全国高中数学联赛的一等奖。在法国里昂高等师范学院数学系念完本科和硕士后，他回校执教。

他所在的华南师大附中是一所奥赛名校。早在1987年，该校学生何建勋就捧回了第28届IMO的铜牌。1993年，经广东省人民政府批准，学校承办了广东省奥林匹克学校，开始在初中、高中招收奥班学生。

这一切都在数学竞赛发展的大背景下展开。现代最早的数学竞赛可追溯到1894年匈牙利举办的比赛。到了1934年，苏联首次将数学竞赛与奥林匹克挂钩。1959年，第一届国际数学奥林匹克竞赛在罗马尼亚拉索夫举行。

3月7日，在华南师大附中上课的IMO中国国家集训队。

中国的数学竞赛始于1956年。当年，北京、上海、天津、武汉举办了四城市高中数学联赛，华罗庚、苏步青等大师参与其中。改革开放后，一场关乎数学竞赛未来走向的大连会议召开，确立了数学竞赛由中国数学会组织实施，是一项群众参与、民办公助的课外活动。1981年起，全国各省市、自治区的高中数学联赛开始举办。

到了1985年，中国也派出了选手首次出征IMO。当时，只有北大附中和上海向明中学的两名学生参赛，但收获了一枚铜牌，这让国内为之振奋。当年底，大家就在思考：如何选拔选手参赛？

1986年，全国中学生数学冬令营应运而生，也就是后来的中国数学奥林匹克竞赛（CMO），来参加冬令营的都是全国高中数学联赛的学霸。首届冬令营在南开大学举办，共有81名学生参加，为期6天。通过冬令营，选出国家集训队员21名，之后，又选出6名国家队选手。

自此，由高中数学联赛到冬令营再到国家集训队，进入国家队，直通IMO的通关路径确立。此后，入选冬令营的人数规模扩大到100多人，并维持了相当长一段时间，国家集训队的人数保持在30人左右。

陈嘉华记得，当年，想要入选冬令营并不容易，即便获得了高中数学联赛的一等奖，每个省也只取前六名。在这样机制下，中国选手开始在IMO比赛中大放异彩。上世纪90年代，中国在超过一半的比赛中获得团体总分的首位。步入2000年后，中国队更开启了“开挂”模式，15次比赛中，13次将团体冠军收入囊中。

当时，学生的参赛热情颇为高涨，每年，高中数学联赛华南师大附中考点的报名人数就有上千人，全国参赛人数达几十万。在全国范围内，除了华南师大附中，武钢三中、人大附中等一批中学也都相继建立了自己的奥赛人才培养模式，成为输送特长选手的基地。

这其中，武钢三中在1980年代末展露锋芒，该校学生在1988年斩获一枚国际数学奥赛银牌，截至目前，共有17名学生在IMO中收获金银牌。1990年代初，湖南师大附中登上舞台，陆续有学生在IMO收获佳绩。步入2000年，上海中学独领风骚。以近10年来入选国家6人组的统计来看，上海中学共有9人次，位列榜首。

这些学校大都为各省市的重点中学，有着良好的生源和师资保障，当地的基础教育水平也相当不错。地域分布上，以近10年来入选国家队与近8年来入选国家集训队的次数统计来看，南方的中学明星多于北方，上海、武汉、长沙等城市成为奥数选手的著名“产地”。

曾在2004年～2011年期间担任中国数学奥林匹克委员会副主席的南京师范大学数学科学学院教授陈永高分析说，竞赛获奖能带来保送的利好，利于学校招生，这使得不少学校领导非常重视，愿意投入精力去做。同时，学校所在地丰富的高校资源也能不时为奥赛发展助力。而南方学校在数学竞赛表现优于北方学校的原因还是教育资源具有优势，当地对于数学教学的重视，以及文化传承方面的影响。

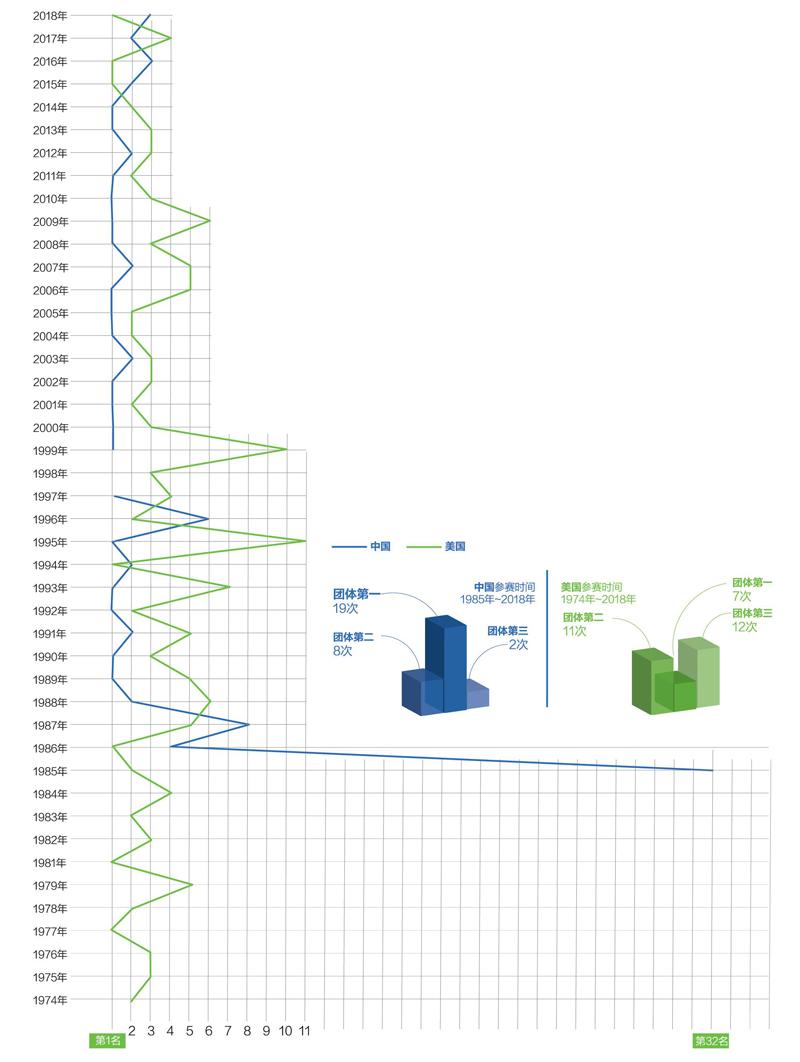
中、美IMO竞赛历次团体排名

华南师大附中数学老师陈嘉华。

陈永高还观察到一个现象：以湖南师大附中为代表的湘军，因竞赛出成绩，产生了一批特级教师，这些金牌名师之后又分赴全国各地，带动了更广范围内奥数竞赛的发展。

在2000年到2004年期间，陈永高曾四次带领中国队参赛IMO，四年里所有参赛选手均获金牌，每年中国队总分均为第一。在他看来，当年取得如此好成绩的重要原因在于，“群众基础比较好，可选学生比较多”，“我们自己老说，即使选出两个队来，都能取得很好的成绩。”

在中学数学竞赛红火的同时，奥数热还蔓延到了小学。标志性事件是1998年，北京小升初实行免试政策，让很多学校把小学奥数当做了入学的重要指标。此后，在校外培训机构的助推下，小学奥数变得一发不可收拾。陈永高说，小学奥数对学生开拓思维有一定作用，但更多是简单的思维训练，而高中数学竞赛更强调知识的全面性和探究性，与前者有着很大区别。

苦乐征程

对于投身数学竞赛的人来说，不少是出于兴趣，在他们眼中，数学是个美丽的存在。

胡浩宇是华南师大附中高三奥赛班的学生，因为参加高中数学联赛进入了省队，获得了北大降至一本线录取的资格。对于数学竞赛的解题过程，他这样描述：“面对一道题目，你不知道怎么能解出来，但就在探索过程中，发现一些题目的特质或结构上美妙的地方，体会到一种乐趣，吸引你往更深的地方探究”，“就像是你走在树林间，一条小路上走过一个转角，然后眼前突然出现了一大片鲜花的感觉”。

一道几何题的建立往往是一步步添加条件从无到有的过程，胡浩宇说，他所做的，就是从有到无，把题目的结论一步步往回逆推，“回到出发点的时候，你就相当于完成了证明。”

乐趣只是硬币的一面，更多的还是坚持和挑战。

2017年的IMO题目中，一道题大意是这样：一个猎人在追击一只兔子，二者最开始距离为一，兔子每步跳动一个单位，探测器返回给猎人的兔子位置与实际至多偏差为一，然后猎人也随之移动一个单位，109 回合之后， 猎人能否确保和兔子之间的距离至多是 100？

题目的每一个字都看得懂，但中国队6名选手在这道题上全军覆没。

从进入冬令营后，學生们面对的都是和IMO竞赛完全一致的考试模式和题型。IMO每次比赛只有6道题，每题7分，包括代数、几何、数论和组合四种类型，每种类型的题目都会有一道，其他两道题的类型随机。6道题平均分配在两天考试中，每天3题的难度依次递增，两天考题的难度相近，每天的考试时间为4.5小时。

现已在北京大学数学学院就读的何天成是华南师大附中2017届的毕业生，也是2017年IMO的金牌得主。在他看来，每个4.5小时都像一场长跑比赛，“看到一道题后，开始会有个突破，但紧接着剩下两小时或更多，可能就是做不出来，它会有一个拉锯阶段，需要更多耐心，到最后半小时，又是一个冲刺阶段”。最惊险的一次，在集训队的考试中，何天成一道题做了三个小时都没结果，最后10分钟化险为夷。

何天成的同学兼战友、同样将IMO金牌收入囊中、现在就读于麻省理工学院的任秋宇，还经历过一次“爆零”，也就是说在一天考试里一道题都没做出来，“所幸在后面一次分数占比较大的考试中，成功逆袭。”

这样“玩的就是心跳”的考试，进入国家集训队后，队员们通常要经历少则三四轮，多则六七轮，题目难度通常要比IMO正式比赛更大。每轮考试间隙，会穿插国家队教练的专题讲座。“一边上课一边考试，最后根据多次的考试成绩，把总成绩最好，也可以说发挥最稳定的选手选出来。”本届国家集训队的教练、曾两次担任IMO领队的复旦大学数学科学学院副教授姚一隽说。

对任秋宇与何天成来讲，走进集训营本身更是一个漫长的过程。任秋宇在高一、高二分别参加了全国高中数学联赛，都只获得了二等奖和一等奖靠后的位置，无缘省队。何天成从初二起，一共参加了五次高中数学联赛，直到高二时，才进入省队，并拿了CMO的金牌，但距离进国家集训队还是差了一名，“名落孙山”。

从参加每年9月举行的高中数学联赛到最终入选国家队要历时半年。平时，准备数学竞赛要耗费大量的精力。“高一、高二大概花70%的时间，高三进入省队后停课备考，几乎全部在准备竞赛。”任秋宇说。

高二数学联赛突围失败后，任秋宇一度迷茫。因为要做出选择，是继续走竞赛路线，还是投奔高考模式。“如果高三参加竞赛还是失败了的话，最后还是得回去高考”。出成绩那天，他到操场上跑了很久，最终，决定继续走下去。数学学科竞赛的教练韦吉珠找他谈了一次话，“（教练说）把以前都抛开，然后从零开始，给我鼓励很大。”

在华南师大附中的奥赛班，教练的角色更像是在体育赛场，使命是给予选手经验上的指导和心理上的抚慰。平时课堂上，他们也更多起提点的作用，主角往往是学生。

奥班的每个竞赛科目都配有专门的教练，到了数学课，教练会带着奥班的二十多名学生单独授课。每周，竞赛班的学生除了常规每天一节40分钟的课程，还有周四下午一个半小时和周六上午半天的专项培训。

陈嘉华的课上，他通常会把要讲的问题提前发下来，让学生充分思考，第二天，学生走上讲台，无论对错，都把想法讲出来和大家分享。有时题目只解出一半，大家帮着共同完成，有时一道题出现了伪证，大家直接指正。

美国奥数队总教练、卡内基梅隆大学副教授罗博深。

这是一个学生和学生间、老师和学生间互相启发的过程。有的课堂上，点到直线的距离学生给出了9种解法，还有题目，学生提出了之前所有解法之外的思路。

带竞赛班的学生并不轻松，意味着老师要尽可能多做准备，更新自己知识体系的速度也要更快。每带完一届学生，奥班的教练们都要重新备课，平时的备课量是普通班的4～5倍。

带奥数班六年以来，华南师大附中的数学教练张琪手边有了上百本资料，“哪位大咖新出了本书，很快教练的书柜里就会有。”

中美差别

2015年起，美国在IMO的比赛上成绩亮眼，除了2017年以外，三次位居榜首。相应地，中国在IMO的团体排名中两次位列第三，两次第二。日前结束的罗马尼亚大师杯数学赛中，美国奥数队总教练、卡内基梅隆大学数学学院华裔副教授罗博深又带队拿了冠军，这是他自上任以来，美国在这一赛事上第三次夺冠。一系列变化引发热议，中美之间奥数是否有了差距，差距在哪儿？

和中国一样，美国的奥数国手同样要经历层层选拔。每年2月，全美数学联赛AMC10/12（10年级或12年级学生参加）举行，参赛人数在20万左右。之后，有将近1万名学生可以晋级到3月底举行的美国数学邀请赛，当中再有500人有资格参加美国奥数竞赛。最终，有约60人进入每年6月举行的美国奥数训练营（MOP），进行为期三周半的IMO赛前培训。

值得注意的是，这些入选的学生都是为来年IMO做准备。入选MOP的预备军团要在当年12月底到第二年4月，再进行每月一次的考试，综合之前的测试成绩，决出国家队的6人组。也就是说，相较中国选手半年的选拔期，美国的奥数国手选拔从一年半前已经开始。在今年国家集训队教练、上海理工大学讲师张思汇看来，这样的机制下，美国选手的稳定性更有保证。

2014年上任前，罗博深已经担任了美国奥数队4年的副领队。2015年，他带队让美国在时隔21年后重获IMO冠军，这被《华盛顿邮报》认为意义堪比1980年的那场“冰上奇迹”——美国冰球队战胜垄断奥运冰球金牌长达40多年的前苏联队。

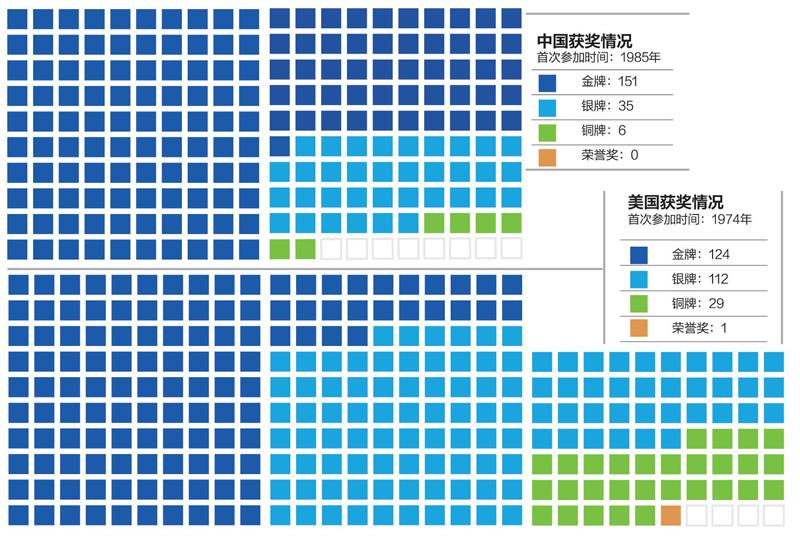
中、美参加IMO竞赛获奖情况

姚一隽分析说，新任主帅罗博深上任后，一个重大变革是修改了选拔规则，将原来只有美国籍高中生才能参赛的规定，改为在美国读高中即可。这在一定程度上短时间内增大了美国队选拔学生的范围。在香港举行的第57届IMO中，美国队夺冠的六名队员中，有两名就是持中国护照的队员。

中国则在另一方向上调整相关政策。2010年底，教育部等五部门发文，取消了高中数学联赛获省级一等奖保送的福利，只有集训队队员才享有保送资格。对此，陈永高指出，“毫无疑问，保送给他们出路，没有保送，家长和学校就不会让孩子们花很多时间在竞赛上。这其中，最重要的又是校长重视，只有校长重视，这所学校的奥数才能搞起来。”

一个更大层面上的数据是：在中国队IMO成绩较好的年份（2000年～2010年），符合参赛条件的人口基数达2000万，而近年来，中国这一数字为1000万左右，姚一隽说，“这样基数的变化还是可观的。”

相较前两任教练，姚一隽还称，在美国长大的罗博深还有着很好的经营能力，也就意味能拉来更多赞助，带给队伍更多训练。6月最后三周，得益于美国大学基本已放假的便利，美国的集训由10名教练、10名助教全程参与，多名教练在不同的教室同时授课，学生根据自身优势短板各取所需，进行自助餐式的学习，整个集训营预算40万美元。而中国集训队的预算则在20万人民币左右，由于人力、财力等原因，集训队教练只能给学生上大课。

十多年来，美国队一直在做的一个事情还在于补短板。从2003年起担任美国队总教练的菲利普斯埃克塞特中学教师冯祖鸣就发明了“重点培养第六名”策略。此前接受采访时，他坦言，“每个国家队都有一两个特别优秀的人，但是没有六个人”，而他所做的“把后面的板凳做强”。罗博深延续了这一战略。

张思汇对此深有感受，“以前比赛，中国队前三名的选手与美国、俄罗斯相比，也未必占优势”，“但对方五六名可能相对差一些，所以我们总分高，但从近5年来看，他们的五六名选手水平也很强。”

在美国奥数集训营中，罗博深组建战队时找来的教练都是之前参加过比赛的年轻人，仅有21岁左右。“找他们的原因在于其最接近于当下学生面临的有关数学和生活方面的挑戰”。在接受《中国新闻周刊》采访时，冯祖鸣将过去参加IMO的学生形容为“百宝箱”，他还称，像IMO这样的训练团队吸纳了不只来自于美国队的选手。而在过去十多年中，美国面向中小学生、以解决问题为导向的社团、机构蓬勃兴起，这都为美国数学竞赛新鲜血液的输送提供了重要支撑。

授课方式上，美国课外的奥数课程也有一番独特讲究。以几何体学习为例，北京师范大学教育学部赵萍副教授在一篇文章中写道：老师会提出基于设计的学习方式，学生们以自己最爱的毛绒玩具为主人公，想象给它搭建一所房子。从设计图纸，到手工搭建，再到给房子内部装上楼梯、分割房子功能、制作家具，这一方式训练了学生结合实际生活情境解决问题的能力，与国内的“刷题”模式大为不同。

此外，相较国内的教育资源不均衡，美国的教育资源则较为分散化，大学对于周边中学教育的参与度较高，这也使得很多课外兴趣小组能由大学老师来组织。

未来之路

姚一隽分析说，纵观近几年的IMO结果，美国队进步明显，而中国选手基本维持在正常水平范围内，但6个人的整体水平略有下降。

如何选出适合数学竞赛的学生，又如何提升其水平？

早在1956年的《数学通报》上，华罗庚就写道：“（数学竞赛）只是给一些有数学才能、在功课以外有余力的学生更高的锻炼机会”。今年IMO的领队、华东师范大学数学系教授熊斌曾多次接受采访时表示，数学竞赛只适合5%的中国学生。

在荷兰阿姆斯特丹举行的一场国际奥林匹克数学竞赛。

但在陈嘉华的观察中，如今的奥数已变得过于功利化，学生学奥数的目的多样，不少人盲目参与进来。中国教育科学研究院研究员储朝晖也表示，“其实真正适合搞竞赛的学生，或者说走这条路，一定是学生自己真正能有兴趣、有意愿去学的，而不是为上一个好学校才去参赛，拿一个奖牌。”

华南师大附中数学教练张琪原本的期望是，学生追求喜欢的东西，做热爱的事情，进而通过数学竞赛的训练来提高思维能力，丰富学生对数学的认识，使其拥有更扎实的知识基础。但实际中，一个班二十多人，真正怀有对数学纯粹热爱的不超过五六个，其他人至多是有着数学特长，甚至还有人以刷题的方式行进，有时候，“热爱的还不一定考得过刷题过多的学生”。

即便在国家集训队，靠套路制胜的现象也依然存在。“不是说所有的问题答案都已经在那里了，其实你到某一个时候，至少是要开始去探索未知的领域的，老想着依靠已有的经验，这是肯定不行的。”姚一隽说，他希望通过命题环节体现题目内容和类型的自由性，让学生能看到，有各种各样的可能性存在，不把思维定势化，“我想这种情况是慢慢可以改变过来”。

另一个需要面对的问题是学生的基本功不扎实。以近年来中国队失分较多的几何题为例，2015年的IMO中，中国队这一题型上输美国队19分，相当于美国队比中国队多3人解出这道题。2013年的CMO，同样是几何证明题，300名全国学霸中，30人弄反了“充分性”和“必要性”。陈永高称，这与近年来的课改不无关系，课改淡化了平面几何，也进而导致了学生“推理和计算能力下降”。

姚一隽认为，现在的难题还在于，学生的培养，如过去大多数重点中学都有的数学兴趣小组一样，本应该是在校内课外，再加上自学进行，但今天有意愿组织校内的师资力量来好好教学生的学校并不比二三十年前更多，甚至有些所谓名校的教练就像经理人一样，基本上只做组织学生听课的工作。“我们应该培训一批有能力的一线教师、建立一套课程体系，但这事该由谁去做，相关方面有没有意愿，都需要探讨。”

储朝晖建议，可发动专业社团、协会等第三方力量的作用，让其加入进来。中国科学院院士、数学家、北京师范大学-香港浸会大学联合国际学院校长汤涛认为，选拔、培养上可与国际先进做法接轨，多一些经费支持，略微拉长一点国家队集训时间，选手们多参加一些别的国家的比赛，互相交流取经。

IMO摘金是不少参赛者的梦想，但这不该是终极目标。罗博深在接受《中国新闻周刊》采访时表示，他更关注的是学生长期发展，以及在20年后能在报纸上读到其为人类发展所作的贡献。

不少研究者眼中，IMO与具有数学界诺贝尔奖之称的菲尔兹奖有着紧密关联。四年一届的菲尔兹奖，近20年几乎每届都有一两位得主有IMO获奖经历。汤涛认为，要找出真正对数学有兴趣的人，从而去培养一部分顶尖数学家。

现实中，还有不少学生在获得IMO金牌后另选他路。2002年、2003年連续两年满分斩获IMO金牌、南方科技大学讲师付云皓曾在文章中发问：如何避免高手因要冲出来过早做太多重复性训练，导致进入大学后不喜欢数学？

储朝晖认为，参与竞赛的真正目的在于了解自己，发现自己，建构自己，实现自己，要避免功利性，保持自主性。不少教练和参赛者认为，参加IMO最大的收获不在于比赛本身，而是培养了自主学习、独立思考、不断探究的能力和做事坚持到底的品质，并对日后发挥作用。

如今，上了北大的何天成，常在图书馆坐冷板凳，盯一页书，思考一整天。上大学前，他从未想过要熬夜，现在却时常为了一个数学问题夙夜不眠。远在麻省理工的任秋宇像小孩子一样对未知保有好奇，立志要做纯数学研究。