通过立体几何教学,提升学生的数学核心素养
梁敏聪
摘 要:《立体几何》是数学重要模块之一,也是难理解内容之一。结合教学实践谈谈在立体几何教学中,重视学法指导,加强解题思路的引导,不断提升学生的数学核心素养。
关键词:数学核心素养;立体几何;解题思路的引导
中图分类号:G633.63 文献标识码:A文章编号:1992-7711(2019)06-075-1
数学核心素养是学生学习过程中形成的体现学科本质的具有一般发展属性的品质与能力[1]。新课标修订组将数学核心素养分解为数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[2]。立体几何是高考考核的重点难点,高一内容多课时紧,新课匆匆而过,高二复习“炒冷饭”似的,刚炒热就过了,高三再来一轮复习,每次接触浅尝而止,成效不大。本文从重视学法指导,加强解题思路的引导进行探讨,进一步提升数学核心素养。
一、重视学法指导,提升学生数学抽象素养
数学抽象素养是指既有将具体对象进行抽象的“数学化”意识,又将具体对象用数学的符号、语言进行表征[3]。數学处处体现抽象,例如函数立体几何等,数学抽象使很多同学望而畏惧,应加强学法指导,克服畏难情绪。
例1.若直线l1和l2是异面直线,l1在面α内,l2在面β内,l是面α与面β的交线,正确的是( )
A.l至少与l1,l2中的一条相交 B.l与l1,l2都相交
C.l至多与l1,l2中的一条相交D.l与l1,l2都不相交
分析:显然l与l1共面,l与l2共面,如果l与l1,l2都不相交,则有l∥l1,l∥l2,推出l1∥l2,显然与大前提l1和l2是异面直线矛盾。中下层学生不是很理解,将抽象的线与面,用书与笔来代替,更容易理解。以打开的书本为道具,拿两支笔来摆,便知分晓,或借助正方体或长方体,以它的棱为线,进行具体判断,从抽象思维慢慢地向逻辑思维过渡,克服畏难情绪,提升数学抽象素养。
二、加强解题思路的引导,提升学生逻辑推理素养
逻辑思维能力强的学生不需要老师点拨就能顺利完成证明题,但中下层学生相当困难,要教会他们解决这一类问题的能力,将已知条件和证明结论结合起来,一步一步地引导学生思考,建立问题的逻辑链条,从而解决问题。
在立体几何证明题中,普遍学生感到,证明垂直比证明平行要难,证明垂直中,证明面面垂直比证明线面垂直要难,因为证明线面垂直,已经知道哪条是垂线,而证明面面垂直需要找垂线,学生不知所措无法动笔。我们在平时教学过程中,循循善诱,加强解题思路的引导,提升数学逻辑推理素养。
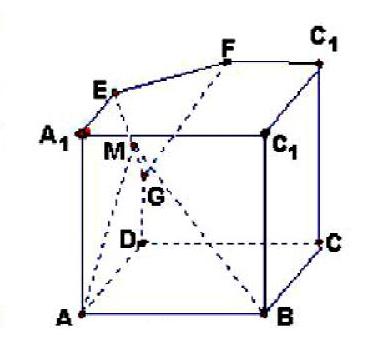
例2.正方体ABCD-A1B1C1D1中E、F、G分别为A1D1、C1D1、DD1的中点,被面EFG所截,M为EG中点,求证:面ABM⊥面EFG
分析: 面EFG有三条线EF、FG、EG,可能有一条为垂线; 或是面ABM三条线AB、AM、BM,可能有一条为垂线;也有可能是辅助线,先考虑现有的线。
大胆假设:(1)若EF⊥面ABM,则EF垂直于面ABM中的任意一条线,则EF⊥AB。而EF∥A1C1,AB∥A1B1,A1C1与A1B1夹角是45°,EF与AB夹角也是45°,与EF⊥AB矛盾,从而排除EF为垂线的可能,AB也不可能是垂线,因为AB连EF都不垂直,更不可能垂直面EFG。
(2)同理FG不可能是垂线。
(3)本想排除EG,在意料之外发现AB⊥面,EG面,故AB⊥EG,因为AB不可能为垂线,EG有可能为垂线,更要关注EG这种本身有垂直关系的线。
(4)MB是体内的线,AM是面上的线,考查证明AM是否是垂线更加方便。若AM⊥面EFG,必有AM⊥EG,下面考查AM⊥EG是否成立,不妨立体图形平面化。连接AE,AG,易证△A1AE≌△DAG(SAS),得AE=AD,等腰三角形三线合一,推导EG⊥AM。结合(4)知EG⊥AB ,得证EG⊥面ABM ,证面ABM⊥面EFG。
逐一排除垂线的方法看起来很“笨”,将问题复杂化。在寻找垂线中给头脑零乱的中下层学生指出了一个明确的方向,当中包含反证法。当然有时不必将所有线都一一排除,至少将考虑范围缩小,更明确哪些线有可能是垂线,本来有垂直关系的两条线,成为垂线可能性更大,更关注它们。展现思维过程,比一开口就说EG是垂线更有说服力,若光讲答案,学生除了惊叹之外一无所获。只有将整个思考过程暴露给学生,循循善诱引导学生解题。
通过立体几何教学,提升直观想象、数学抽象、逻辑推理素养,但这不是一朝一夕的事,我们必须有耐心,循序渐进,重视学法指导,加强解题思路的引导,才能让学生学好立体几何。
[参考文献]
[1]杨建楠.数学核心素养在“问题——互动”教学中的培育[J].教学与管理(中学版),2016(9):52.
[2]中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:4.
[3]石志群.对数学核心素养几个问题的思辨[J].教育研究与评论·中学教育教学,2016(11):17.

