拖拉机动力输出轴载荷经验模态分解软阈值降噪研究

闫祥海,周志立,李忠利

(河南科技大学车辆与交通工程学院,471003,河南洛阳)

拖拉机旋耕作业动力输出轴(PTO)载荷是多分量非线性、非稳态信号,有效分离载荷中的噪声是载荷数据处理及有效使用的关键[1]。传统尺度滤波降噪方法通过对载荷的频谱分析,利用先验知识人为选取截止频率,设计滤波器,消除噪声频带[2-3]。截止频率的选取依赖对实测信号频率成分的预判。卡尔曼滤波降噪方法需要对噪声成分、噪声方差等信息准确分析,以预判噪声先验统计特性[4]。小波滤波降噪方法需要根据数据特性对小波基、分解尺度人为选取[5]。拖拉机PTO载荷测取受测试工况、测试环境因素的影响,噪声成分复杂,无法对载荷特性进行预判,以上降噪算法均不能对拖拉机PTO载荷进行有效降噪。经验模态分解(EMD)属于自适应数据驱动算法,人为干预因素少,可将载荷进行时域和频域的多尺度分解,得到固有模态函数(IMF)[6-8]。利用相关系数[9]、能量熵[10]、排列熵[11]等性能指标区分噪声主导IMF分量,通过对噪声主导IMF分量进行小波、阈值降噪[12],既客观区分了噪声,又保留了噪声主导分量中的有用成分。针对EMD分解中出现的端点效应,有学者从载荷原始数据的延拓和预测两方面提出了多种抑制端点效应的方法,对不同类型数据得到了理想的EMD分解结果[13-15],EMD降噪方法在工程领域得到了广泛应用。

本文在分析EMD软阈值降噪原理的基础上,对拖拉机旋耕作业PTO转矩载荷进行降噪研究。采用边界局部特征尺度延拓算法抑制PTO载荷EMD分解产生的端点效应,利用相关系数辨识噪声主导IMF分量,通过对噪声主导IMF分量软阈值降噪,实现拖拉机PTO载荷降噪。

1 EMD软阈值降噪原理分析

EMD软阈值降噪算法综合EMD理论与阈值降噪理论,根据数据自身特性对信号进行自适应处理,算法包括EMD分解、端点效应抑制、IMF分量划分、软阈值降噪。对PTO载荷S(t)进行EMD软阈值降噪的原理及流程如下。

(1)寻求S(t)极大值点和极小值点,利用3次样条函数拟合得到极大值包络线m+(t)和极小值包络线m-(t),求出S(t)均值包络线

a1(t)=[m+(t)+m-(t)]/2

(1)

(2)由S(t)减去a1(t)得到新序列h11(t),判断h11(t)是否满足IMF两个定义条件:

整个数据序列中IMF函数过零点数和极值点数相等或至多相差1;

任意时刻m+(t)和m-(t)关于时间轴对称。

若满足条件,h11(t)即为S(t)一阶IMF分量;否则,将h11(t)视为原始序列,重复步骤(1)、(2)。经过k次循环,hk1(t)满足IMF定义条件,则得到S(t)一阶IMF分量

C1(t)=hk1(t)

(2)

(3)新序列r1(t)由S(t)减去C1(t)得到,对r1(t)重复步骤(1)、(2),得到S(t)二阶IMF分量C2(t)。照此循环n次,得到S(t)的n个IMF分量Cm(t)和残余量rn+1(t),当rn+1(t)为单调函数时,分解终止。S(t)可表示为

(3)

(4)判断分量Cm(t)是否出现端点效应,若出现,进行端点处理,文中采用边界局部特征尺度延拓算法进行端点处理[16]。记S(t)左端第i个极大值为lmaxi,该极大值对应的序列点为find(lmaxi)

L=(lmax4-lmax1)/3

(4)

S(t)左端延拓极大值的序列点为

find(Lmax)=find(lmax1)-find(L)

(5)

S(t)左端延拓极大值为

(6)

至此,得到S(t)左端延拓的极大值位置与幅值。类似的方法得到左端延拓的极小值,右端延拓的极大值、极小值的位置与幅值,然后循环步骤(1)～(3)。若分量Cm(t)没有出现端点效应则进行步骤(5)。

(5)文中利用IMF分量Cm(t)与S(t)相关系数区分噪声主导IMF分量与PTO载荷主导IMF分量。相关系数定义为

(7)

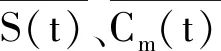
(6)计算噪声主导IMF分量EMD去噪阈值[17]

τm=med{|Cm(t)-

(8)

式中:τm为Cm(t)阈值;med(·)表示中值函数;M为S(t)时间长度。

(7)EMD软阈值去噪表达式为

(9)

(8)重构得到降噪后信号

(10)

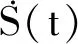
2 EMD软阈值降噪算法应用

根据EMD软阈值降噪流程,对田间实测的拖拉机PTO载荷进行降噪处理,验证EMD软阈值降噪算法在PTO载荷降噪中的适用性。

2.1 PTO载荷测取及EMD分解

对拖拉机配套1GQN-230ZG型号旋耕机进行了田间旋耕作业试验,采用HDT05转矩传感器检测PTO载荷,数据采集器获取传感器数据并传输至上位机软件进行数据显示、保存及分析。试验中耕深为130 mm、耕幅为2 300 mm,油门开度为75%,发动机转速为2 000 r/min,拖拉机作业速度为4～5 km/h,PTO转速范围为650～700 r/min,地面条件为耕后的黏砂壤土。PTO载荷频率一般在20 Hz以内[3],根据Nyquist采样定理及工程应用经验,数据采集器采样频率设置为200 Hz,数据采集系统稳定运行时截取1 600个测量点,拖拉机PTO载荷如图1所示。

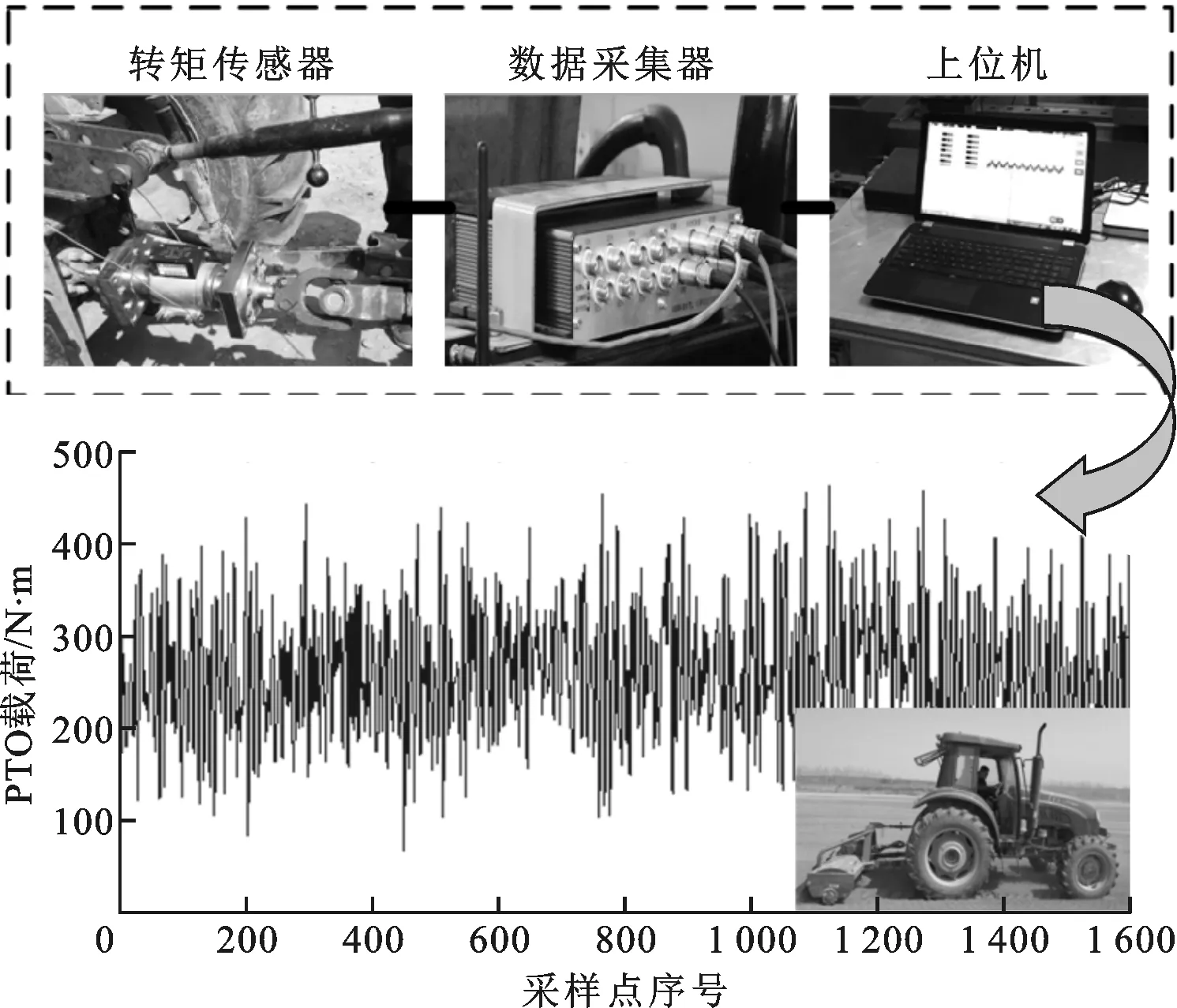
图1 拖拉机PTO载荷

根据EMD软阈值降噪算法中步骤(1)～(3)对拖拉机PTO载荷进行EMD分解。在IMF定义条件基础上,参考PTO载荷实际分解过程,设置分解终止条件为:每个IMF最大迭代次数为100;载荷平均值与包络幅值的比值小于阈值0.5;载荷平均值与包络幅值比值大于阈值的信号数与信号总数之比小于阈值0.5。

满足以上任一条件,分解终止。采用以上分解终止策略得到7阶IMF分量和一个残余量,如图2所示。

图2 PTO载荷EMD分解分量

由图2可知,EMD分解方法将拖拉机PTO载荷分解为高频到低频的分量,由于EMD分解是基于数据驱动的分解方法,分解过程依赖极值点的选取,如果PTO载荷数据两端点处数值不是极值点,在3次样条插值过程中端点处会存在发散,导致EMD分解中出现端点效应。图2中IMF3分量与IMF4分量在端点处出现明显的数据发散(圆圈标注部分),且污染内部数据,IMF4中数据超出载荷范围。由于端点效应的存在,出现虚假分量,使得载荷分解阶数较多。

2.2 PTO载荷端点效应处理

根据EMD软阈值降噪算法中步骤(4)进行PTO载荷端点效应处理。PTO载荷与旋耕机刀轴旋转频率有关,可认为是准周期信号,而镜像对称延拓算法[18]与多项式拟合延拓算法[19]对准周期信号EMD分解的端点效应处理结果较好,因此利用这两种算法与本文采用的边界局部特征尺度延拓算法进行对比分析。

镜像对称延拓算法中,由于PTO载荷左端第一个极值点为极小值,且第一个采样点值大于第一个极大值,因此取第一个采样点为对称点镜像运算。PTO载荷右端最后一个极值点为极小值,且最后一个采样点值小于最后一个极大值,因此取右端最后一个极小值点为对称点镜像运算。多项式拟合延拓算法中,取PTO载荷左端前3个极大值进行二次多项式拟合得到拟合方程,计算拟合方程在原点处的函数值,该值为左端延拓极大值。利用类似的方法得到左端延拓的极小值、右端延拓的极大值和极小值。

将以上3种方法得到的延拓点与PTO载荷组合,得到新数据并进行EMD分解。以算法运行时间、正交指数及IMF数量为评价指标对比分析3种算法性能,结果如表1所示。正交指数定义为

(11)

式中:p、k为IMF分量序号;i表示序列点数据序号。正交指数代表了信号能量丢失、IMF分量信号重叠的程度,正交指数越小,算法性能越优。

对图2中出现端点效应明显的IMF3分量进行3种算法的端点局部对比,如图3所示。

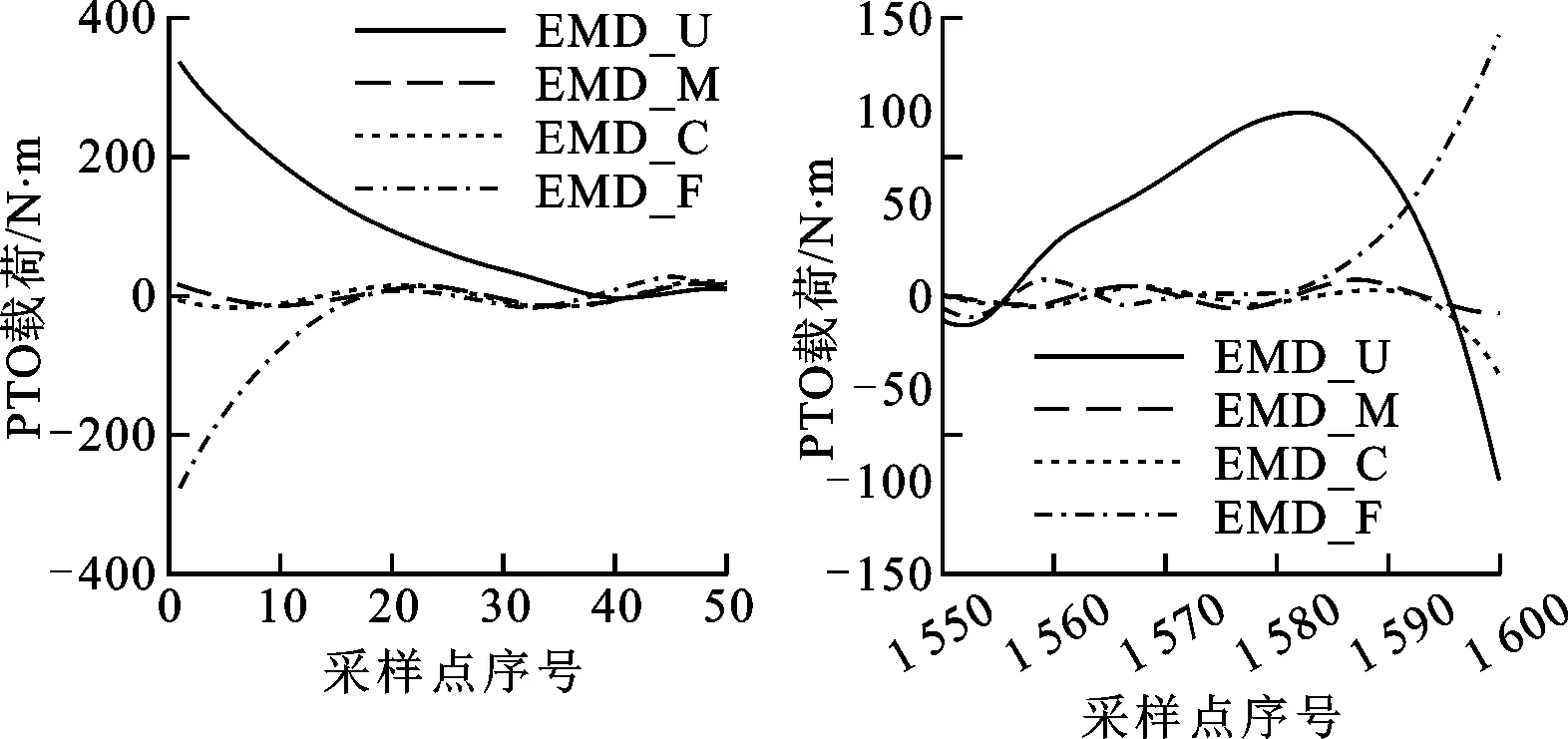
(a)左端点 (b)右端点图3 3种算法在IMF3分量端点局部处理的结果

由表1和图3可得,边界局部特征尺度延拓算法从PTO载荷全局搜寻延拓点,一定程度上保留了PTO载荷特征,EMD分解结果较其他两种算法在3项评价指标与端点局部处理中均占优势。PTO载荷采用边界局部特征尺度延拓算法的EMD分解结果如图4所示。

表1 3种端点效应处理算法EMD分解性能对比

注:EMD_U表示未进行端点处理的EMD分解;EMD_C表示边界局部特征尺度延拓算法进行端点处理的EMD分解;EMD_M表示镜像对称延拓算法进行端点处理的EMD分解;EMD_F表示多项式拟合延拓算法进行端点处理的EMD分解。

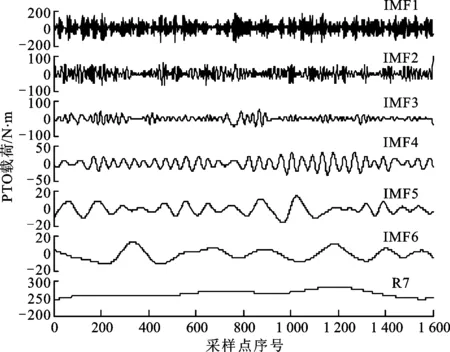
图4 载荷边界局部特征尺度延拓EMD分解分量

图4中,PTO载荷分解得到6阶IMF分量和一个残余量,与图2对比,IMF分量数减少,IMF3、IMF4中端点效应明显改善。

2.3 PTO载荷软阈值降噪

根据EMD软阈值降噪算法中步骤(5)～(8)进行PTO载荷软阈值降噪。利用式(7)可得前3阶IMF分量与实测载荷相关系数均小于0.3,属于微相关,认为是噪声主导分量。利用式(8)可得IMF1分量阈值为115.588,IMF2分量阈值为50.450 7,IMF3分量阈值为29.696。利用式(9)对前3阶IMF分量进行软阈值降噪,利用式(10)得到软阈值降噪后的PTO载荷如图5所示。

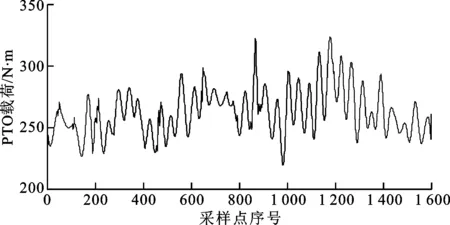
图5 EMD软阈值降噪PTO载荷

3 EMD软阈值降噪结果分析

为对比EMD软阈值降噪效果,对图4中6阶IMF分量和一个残余量进行单一尺度滤波降噪。根据截止频率不同,构造6个PTO载荷低通滤波算法(序号为1～6),6个PTO载荷高通滤波算法(序号为7～12)及15个PTO载荷带通滤波算法(序号为13～27),以均方根误差为评价指标对27种尺度滤波降噪算法进行对比分析。图6为均方根误差归一化后的对比结果。

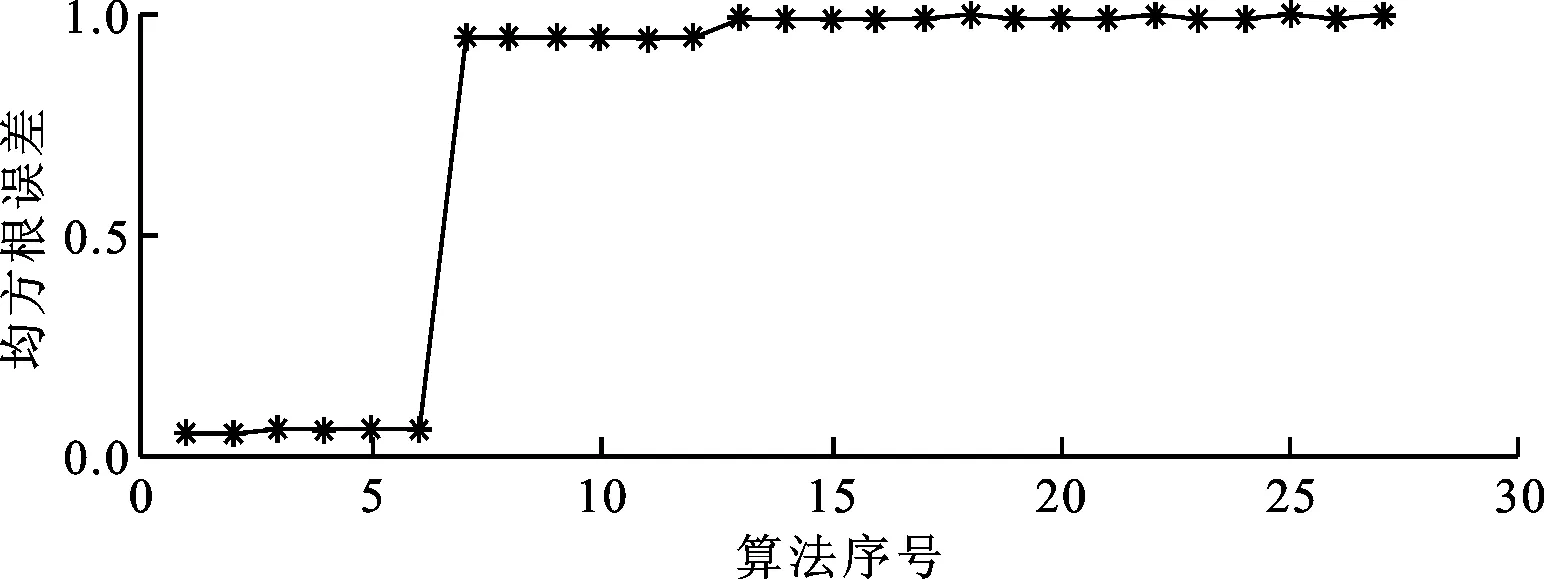
图6 尺度滤波降噪算法对比

图6中,低通滤波算法相比高通、带通滤波算法的归一化均方根误差小,该结果同时验证了PTO载荷主要分布在低频IMF分量中的判断。文中选取归一化均方根误差最小的低通滤波算法作降噪效果对比。

定义含噪信号与噪声误差比为

(12)

以dnSNR为降噪性能评价指标,对EMD低通滤波降噪与EMD软阈值降噪效果进行评价。由式(12)得,EMD低通滤波降噪与EMD软阈值降噪的dnSNR分别为13.266 6、12.712 5。EMD软阈值降噪的dnSNR较小,说明降噪后载荷远离实测载荷,降噪明显。

对PTO载荷、低通滤波降噪及软阈值降噪后的PTO载荷进行频谱分析,结果如图7所示。

图7 降噪前后PTO载荷频谱图

由图7可见,EMD软阈值降噪后载荷频谱中幅值最大处频率接近5 Hz,试验中旋耕机刀轴转速为300 r/min,刀轴旋转频率为5 Hz,与图中幅值最大处频率相符,因此频率4.492 Hz应为PTO载荷频率。EMD低通滤波降噪后PTO载荷存在多处幅值较大的高频噪声,同时包含PTO载荷,降噪效果较差。EMD软阈值降噪后高频噪声几乎为0,以PTO载荷为主,降噪效果较好。采用EMD软阈值降噪保留了幅值较大的低频信号,该低频信号为旋耕机受到的随机冲击载荷,可对载荷谱编制及PTO寿命预测起重要作用。

4 总 结

拖拉机旋耕作业PTO载荷混杂多种高频噪声,载荷EMD分解时会出现端点效应,采用边界局部特征尺度延拓算法可有效抑制端点效应,与镜像对称延拓算法和多项式拟合延拓算法对比,在算法运行时间、正交指数及IMF分量数3项性能指标中均占优势。

EMD软阈值降噪算法通过对EMD分解后的噪声主导IMF分量进行软阈值降噪,能够细分载荷频率,且降噪过程属于自适应数据驱动,不需要设定截止频率。与EMD低通滤波降噪算法相比,EMD软阈值降噪方法得到的含噪信号与噪声误差比较小,降噪效果明显。

PTO载荷频率与旋耕机刀轴旋转频率一致,且包含幅值较大的低频载荷,该低频载荷应为旋耕机受到的随机冲击载荷。文中采用的EMD软阈值降噪算法及降噪评价指标dnSNR对农业机械田间实测载荷的处理具有一定参考作用。