黏性土地层中盾构隧道开挖面极限支护力理论解

李 奥，张顶立，孙振宇，曹利强，李 然

(北京交通大学 城市地下工程教育部重点实验室，北京 100044)

在盾构掘进时维持开挖面稳定是保证安全施工的重点，开挖面一旦失稳将伴随着地层过度变形和塌陷，甚至引发周围建筑物破坏等一系列严重后果。当盾构在城市软土隧道施工时，因开挖面自身不能维持稳定而需施作支护，因此合理确定盾构隧道开挖面极限支护力尤为关键[1]。

开挖面极限支护力理论分析方法主要集中在开挖面破坏模式的确定和极限支护力的计算上。其研究过程：先构造合适的开挖面失稳破坏模式，然后基于极限分析法、极限平衡法等方法，推导出开挖面的极限支护力。由于极限分析法计算过程和结果都较为复杂，难以推广应用，而极限平衡法因其计算简便、推导过程简单而在盾构隧道设计中被广泛用于计算极限支护力。Horn[2]首先提出了均匀软质地层隧道开挖面稳定性的楔形体计算模型。在Horn模型的基础上，Jancsecz等[3]考虑楔形体上部土体松动土压力，计算开挖面极限支护力。吕玺琳等[4]通过建立常规楔形体模型(破坏面为垂直滑移面)，对盾构隧道开挖面极限支护压力进行了解析。魏纲等[5]、胡雯婷等[6]基于砂性土的成拱效应和开挖面破坏形态，对常规楔形体模型进行适当改进。综合现有研究成果可见，当前的开挖面稳定性研究多基于砂性地层开展，对于黏性土层的研究较少，且模型试验和数值模拟的结果表明黏性土与砂性土的开挖面破坏形态差异较大[7-8]。

本文基于黏性土地层条件下盾构隧道开挖面模型试验和数值模拟的失稳破坏形态，对常规楔形体模型进行修正，建立棱柱楔形体模型，通过极限平衡法得出盾构隧道开挖面极限支护力的显式表达式，同时将本文解析解与数值分析解、现有理论解、离心试验结果进行对比。

1 黏性土层盾构开挖面失稳破坏过程

通过开挖面破坏模型试验研究[7]，得出了黏土地层中浅埋隧道整体破坏模式，见图1(a)。当开挖面缺乏有效的支护力，开挖面产生破坏，向前上方发展逐步破坏到地表，最后开挖面正前方呈现由隧道仰拱向上部和两侧扩展，下部较窄、上部较宽的盆状破坏，这与离散元数值模拟结果[8]一致，见图1(b)。

图1 黏性土层开挖面破坏模式

2 黏性土地层开挖面楔形体模型修正

2.1 楔形体模型修正

常规楔形体模型所假设的破坏面为垂直滑移面，这种假设在密实砂土地层中具有很好的适用性。而对黏性土地层，开挖面失稳对周围土体产生扰动，使得在上部黏性土层中呈现明显的盆状破坏模式，破坏形式表现为开挖面前方为楔形体，破坏区域顶部为棱柱体，见图2。其中：D为隧道直径，B为楔形体的宽度且B=D，α为楔形体滑块破裂角。

由于常规楔形体模型没有考虑到土体破坏的滑切面是前倾和后倾的，因此楔形体上方受力较小，使得所推导出的极限支护力的理论值较小，预测过于保守，不利于隧道安全控制。因此本文对常规楔形体模型进行如下修正：开挖面破坏由靠近隧道底部的楔形体开始诱发，上部以梯形的棱柱破坏逐渐延伸至地表。

2.2 开挖面极限支护力推导

2.2.1 上覆土层松动土压力计算

松动土压力的计算大多是基于太沙基理论进行的[3]，本文建立一个与棱柱滑块平衡模型协调的松动土压力计算模型，三维空间中的松动土压力模型见图3。在松动土压力计算中，关于静止侧向土压力系数k0，对于正常固结黏性土可以按k0=0.95-sinφ[6]计算，φ为土体的内摩擦角。

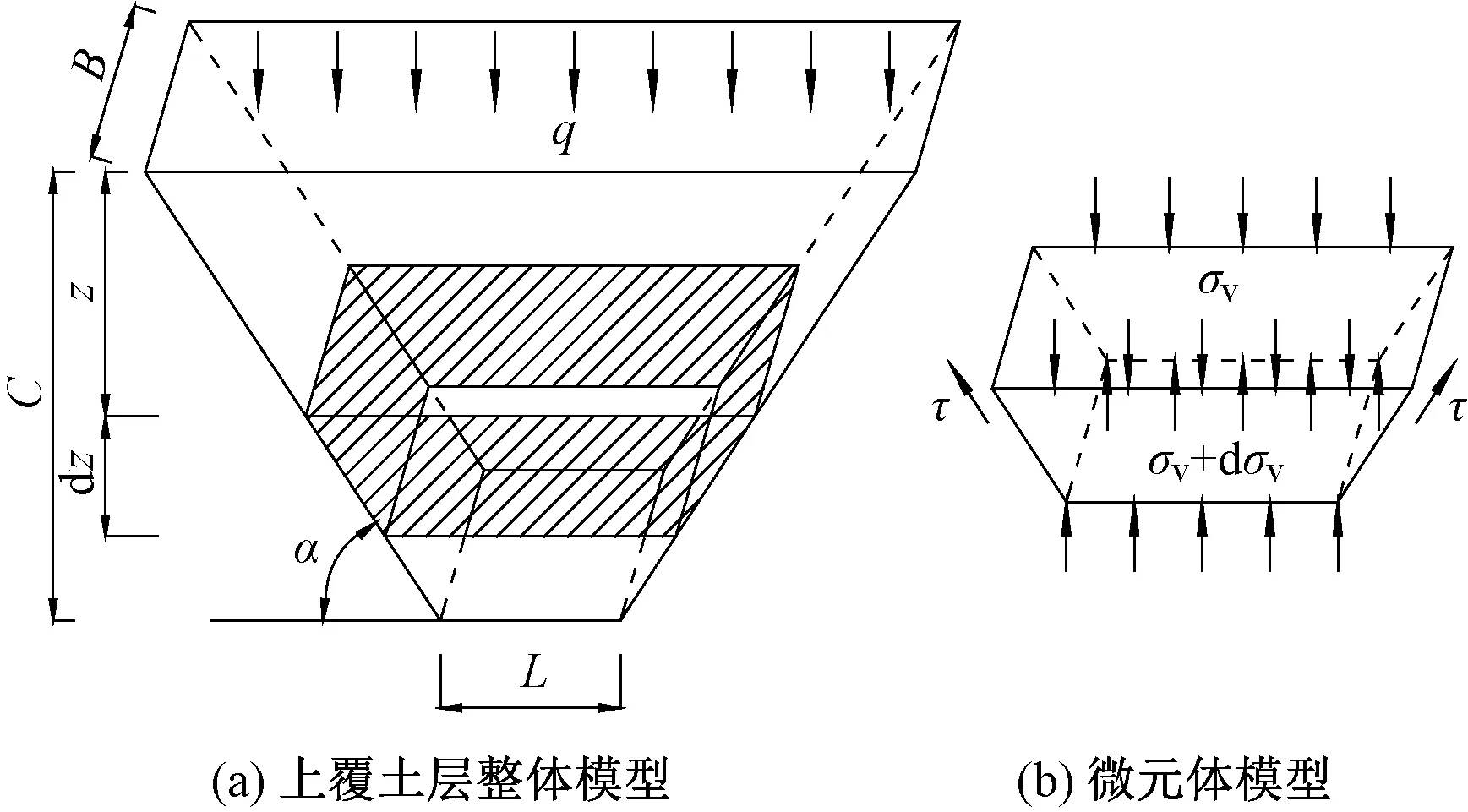
图3 上覆土层松动土压力计算模型

根据图3的上覆土层松动土压力计算模型，利用微元体建立竖向应力平衡方程为

式中：σv为楔形体上表面的松动土压力;z为微元块体距离地表的深度，dz为微元块体的厚度；γ为土体的重度；c为土体的黏聚力；L为上部棱柱底部的宽度，L=B/tanα；C为隧道埋深；A为微元体上截面面积；τ为周围土体对微元体的剪切力。

整理可得

(4)

求解微分方程，并根据已知边界条件,z=0时σv=q，q为地面荷载，得出任意深度处的松动土压力。将z=C代入式(4)，可得σv为

(5)

2.2.2 楔形体受力分析

对下楔形体进行受力分析，如图4所示。

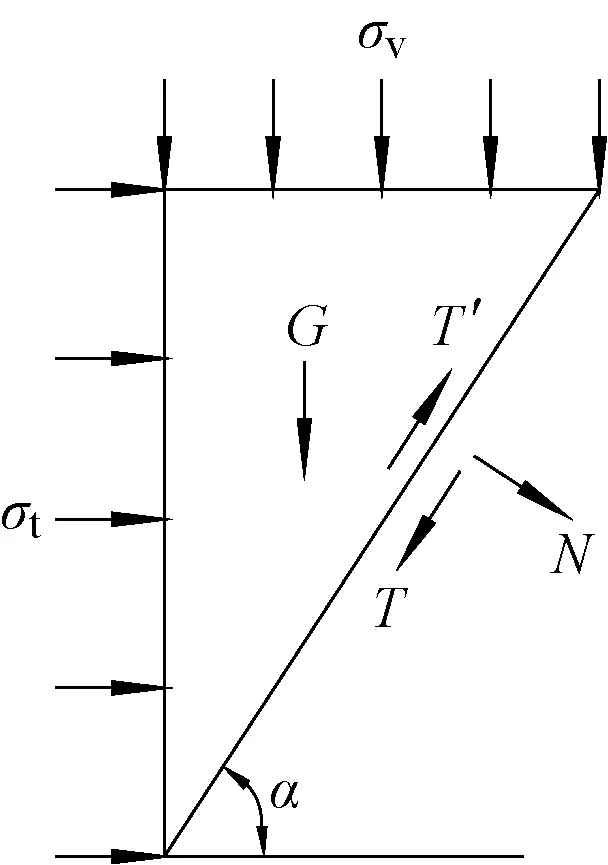
图4 下楔形体受力分析

根据滑块水平与竖向的受力平衡，可得

(6)

式中：σt为开挖面极限支护力;G为楔形滑块重力;N为楔形滑块面的法向作用力;T为楔形滑块面摩阻力;T′为楔形滑块侧面摩阻力。

求解得

(10)

将式(5)带入式(10)，参照太沙基地基承载力三项叠加的形式，将土体黏聚力、地面超载和土体重度对隧道开挖面支护压力的贡献叠加，所以极限支护压力σt的表达式为

σt=cNc+γDNγ+qNq

(11)

式中：Nc，Nγ，Nq分别为土体的黏聚力c、土体重度γ和地面荷载q对极限支护压力的影响系数。

3 计算结果验证与分析

3.1 本文解析解与数值分析解的对比

3.1.1 数值分析方法

采用FLAC 3D数值软件进行分析，研究开挖面极限支护力。具体过程为：一次开挖到指定位置，并施作初期支护，迭代计算使模型平衡，然后逐渐释放开挖面处的应力。为了提高分析效率，应力释放率从0均匀变化到1，记录不同应力释放率情况下开挖面中心水平位移，见图5。

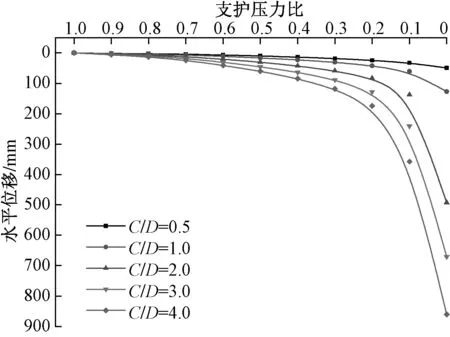
图5 隧道开挖面中心水平位移与支护压力比的关系曲线

文献[7]提出依据隧道中心线水平位移与支护压力比的关系曲线通过多因素敏感性分析，确定开挖面破坏极限状态的支护压力比。以C/D=2.0为例，对敏感度因子S进行三次多项式拟合，其中拟合适应度为0.99，拟合多项式为

(12)

使d2S/dλ2=0，求得敏感度因子与支护压力比曲线曲率发生变化的点，得出极限支护压力比为0.19。

3.1.2 结果对比

用3.1.1节方法得到开挖面的极限支护压力比λ，通过σt=λγH，可以得出开挖面极限支护力σt，其中H为开挖面中点处的覆土深度。为了验证本文解析解的精度，将本文解析解与数值分析解从埋深、黏聚力和内摩擦角多个角度进行对比，对比结果见图6。

图6 不同埋深、黏聚力和内摩擦角下本文解析解与 数值分析解的对比

分析图6可知：

1)极限支护力与隧道埋深呈线性关系，本文解析解与数值分析解误差较小，低于10%，且本文解析解略大于数值分析解。同时，随着埋深的增大，本文解析解与数值分析解误差呈现先减小后增大的趋势，当C/D=2.0时误差最小，表明本文的解析解适用于埋深较小的黏性土层。

2)随着黏聚力的增加，两种解下的极限支护力减小。这是由于黏聚力较大时，滑动面处土体的约束力较大，使得开挖面不需要较大的支护力就可以达到稳定的状态。随着黏聚力的增大，两者的误差减小。

3)内摩擦角较小时两者的结果较为接近，误差低于5%，而内摩擦角较大时两者差异较大，最大误差为32%。表明本文解析解在内摩擦角较小时精度较高，这也说明本文解析解适用于内摩擦角较小的黏土土层。

3.2 本文解析解与既有理论解的对比

选取了黏性土层开挖面极限支护力的既有理论解，包括常规楔形体解[3]、Leca上限解[9]、Vermeer解[10]，并将本文的极限支护力解析解与之进行对比，验证本文解析解的精度和适用性。在不同埋深与内摩擦角情况下，本文解析解与既有理论解的对比见图7。

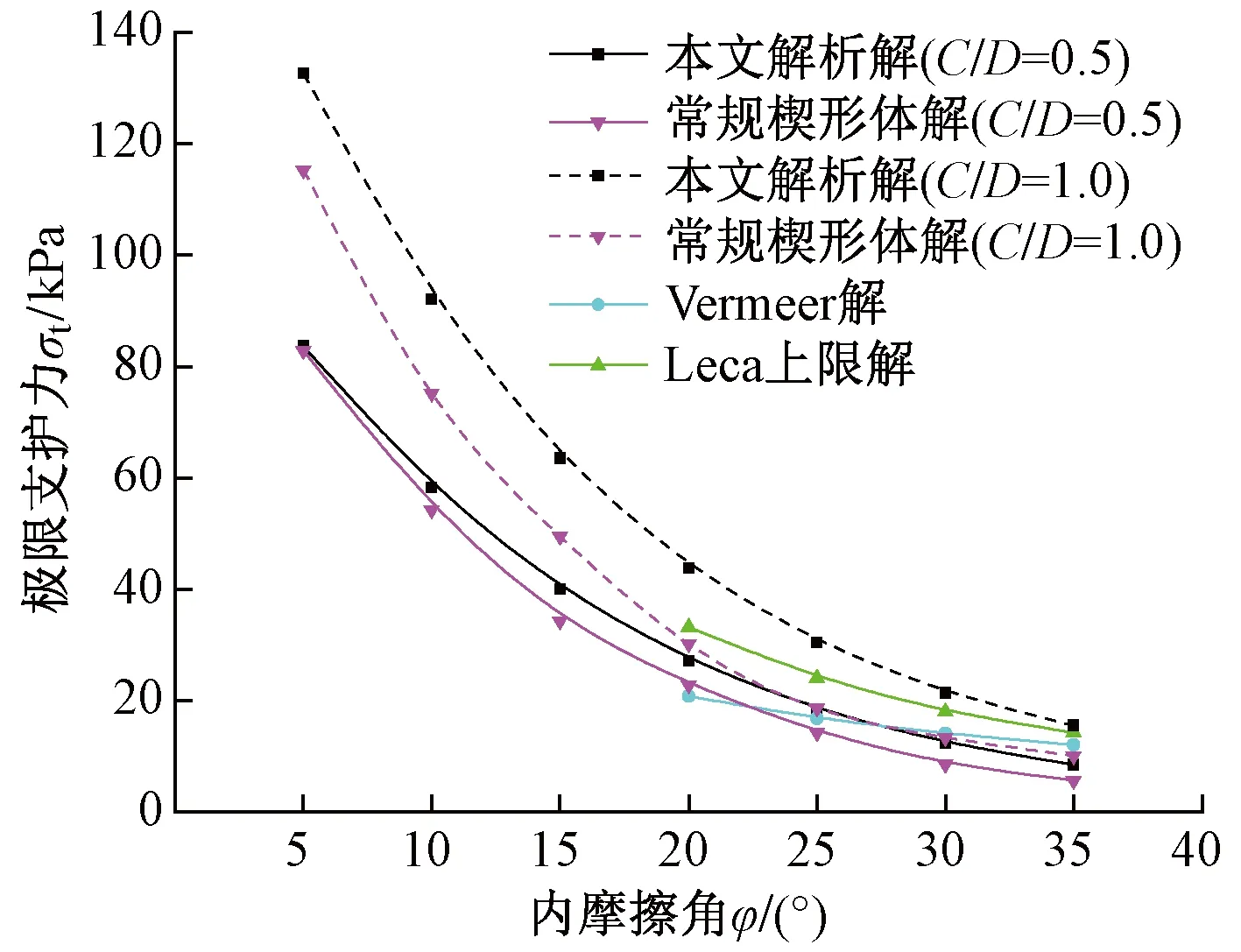
图7 极限支护力对比

由图7可见：

1)本文解析解与常规楔形体解随内摩擦角变化趋势一致，本文解析解大于常规楔形体解。随着隧道埋深的增大两者的差异变大，这是由于本文解析解基于黏性土层的实际破坏范围所得到的楔形体上方的松动土压力大于常规楔形体解，埋深越大时楔形体受到的竖向土压力差异也越大，从而使得本文推导的极限支护力大于常规楔形体解，因此在实际的黏性土层中采用本文解析解得到的极限支护力是安全的。

2)由于Leca上限解和Vermeer解的适用范围在φ≥20°。当C/D=0.5时，本文解析解与Leca上限解和Vermeer解的差异较小；当C/D=1.0时，差异较大。由于Vermeer解是经验公式，与埋深无关，适用范围有一定的局限性。本文经过对比，认为Vermeer解适用于埋深极浅的黏性土层。

3.3 本文解析解与离心机试验结果对比

离心机试验结果未考虑内摩擦角，因此从埋深角度，将本文解析解与离心机试验结果[11]进行对比，见图8。

图8 本文解析解与离心机试验结果对比

由图8可见：本文的解析解与离心机试验结果吻合程度较高，且当埋深增大时两者误差减小，当C/D≥1.0，误差低于10%。表明本文推导的黏性土开挖面极限支护力的解析解具有很好的精度。

4 结论

盾构隧道开挖面稳定研究的关键在于支护压力的确定，本文根据黏性土层中盾构隧道开挖面的实际破坏形式，对现有楔形体模型进行改进，推导了极限支护力的表达式，并与其他方法进行对比分析。主要结论如下：

1)对于黏性土层，改进常规楔形体模型为棱柱楔形体模型，开挖面破坏由靠近隧道底部的楔形体开始诱发，上部以梯形的棱柱破坏逐渐延伸至地表。

2)本文理论计算结果与数值计算结果误差总体上低于10%，在内摩擦角较小和埋深较小的黏土土层中尤为适用。

3)通过与既有研究成果进行对比分析表明，本文的极限支护力解析解是可靠的。棱柱楔形体模型极限支护力的解析解大于常规楔形体解，因此黏性土层中采用本文解析解进行隧道设计更为安全。