基于灰色聚类法的合肥市空气质量综合评价研究

贺爱香，魏巧玲，范奎奎，丁孟琴

(安徽新华学院信息工程学院，安徽合肥230088)

随着我国经济的快速发展和城镇化进程的加快，空气质量呈现出明显的区域性特征。合肥市位于中国中东地区，经济发展日新月异，生态环境的压力随之加大，主要影响因素表现为城市人口、工业、资源消耗和机动车总量等[1]。环境治理已被政府作为提高人民生活质量和改善民生的重点工作[2]。近年来，合肥市委、市政府高度重视城市环境质量，提出了一系列治理城市环境空气质量的措施，虽然城区环境空气质量有所改善，但合肥市空气质量整体水平在全国省级城市中排名仍然靠后[3]。中国的空气污染主要来源于煤制能源结构和汽车尾气排放，其重要因素指标是SO2、NO2、NO、O3、PM10、PM2.5等。由于环境空气质量受众多因素的影响，建立科学的监测评价指标模型是一个多维度的复杂模糊问题，利用灰色聚类法建立评价模型并比较分析对环境质量的有效管理具有重要的实践和理论意义[4]。

国内外学者对空气质量评价进行了大量的模型研究和对比分析。如丁卉等在对广州的空气质量进行评估时，使用了叠加权重的灰色聚类方法，同时通过模糊综合评估和阶段数对城市空气质量进行了定量评估[5]；高明等通过分析北京市空气质量得出影响空气质量因素是由产业结构、工业污染源排放和气象要素相互作用而形成[6]；刘杰等利用灰色聚类模型评价了北京市6类污染物的环境空气质量，为城市环境的治理提出了指导性的建议[7]；陶源盛等学者根据成都市空气中3种主要污染物PM10、SO2和NO2的数据样本，采用模糊综合评价法和灰色关联分析法对空气质量进行评价，通过分级和定性检验确定影响空气质量的主要因素[8]。进行空气质量评价还有其他方法，例如物源分析[9]和神经网络模型法[10]等，其中物源分析法没有对评价因子的权重问题进行深入探讨，而模糊评判法中应用了不确定的最大隶属函数。对于具有更好稳定性的神经网络，需要训练大量的样本数据和客观标准来确定隐藏层的数量，所以提出一种改进的灰色聚类评价模型准确评价城市空气质量等级是非常有必要的工作。

1 合肥市空气质量评价模型建立

1.1 灰色聚类建模基本原理

一般情况下，同一类观察对象的集合可以用作一个集群。灰色聚类是使用灰色关联矩阵或灰色数量的白化权重函数对检测对象进行分类。通过建立目标指标的白化权重函数来反映集群中的级别指标值的间隔值[11]。本文提出的城市空气质量评价模型是在灰色聚类的应用范围中改进了灰色白化权重的聚类方法，然后进行分析和对比。灰色聚类的定义可以描述为有n个聚类对象，m个指标，s个不同灰类，根据第i（i=1，2，…，n）个对象关于j（j=1，2，…，m）指标的实际观察值，将i个对象分类为t，t∈{1,2，…，s}个灰类[12]。灰色聚类的整体思路是构建转换灰色信息的白化权函数，转化过程同时兼顾信息中各类指标的权重。聚类系数就是聚类对象的类别隶属度，使用最大隶属度原则来计算类别。本研究中的监测数据来源于合肥市环境保护局实时自动检测站点，严格按照国家标准，以合肥市空气质量状况中各污染物浓度每日平均值为样本，构建灰色聚类评价模型并进行分析[13]。

1.2 聚类白化数量和分类标准的确定

抽样空气质量监测数据来自合肥市10个自动检测站，分别是明珠广场地区、三里街市区、琥珀山庄住宅区、董铺水库环境保护区、长江中路街区、庐阳区政府、瑶海工业区、包河区、滨湖新区和高新区站点。结合国家《环境空气质量标准》（GB3095-2012），确定 NO2、SO2、CO、O3、PM10、PM2.5为空气质量评价因子，即为灰色聚类的聚类指标j（j=1，2，…，6）。根据城市空气质量指标将空气质量指数（AQI）取值范围定为0～500，划分为6个等级，即0～50、51～100、101～150、151～200、201～300和大于300，分别对应于I、II、III、IV、V和VI级国家空气质量标准中污染物浓度限值的日平均值，具体6个等级如表1所示。

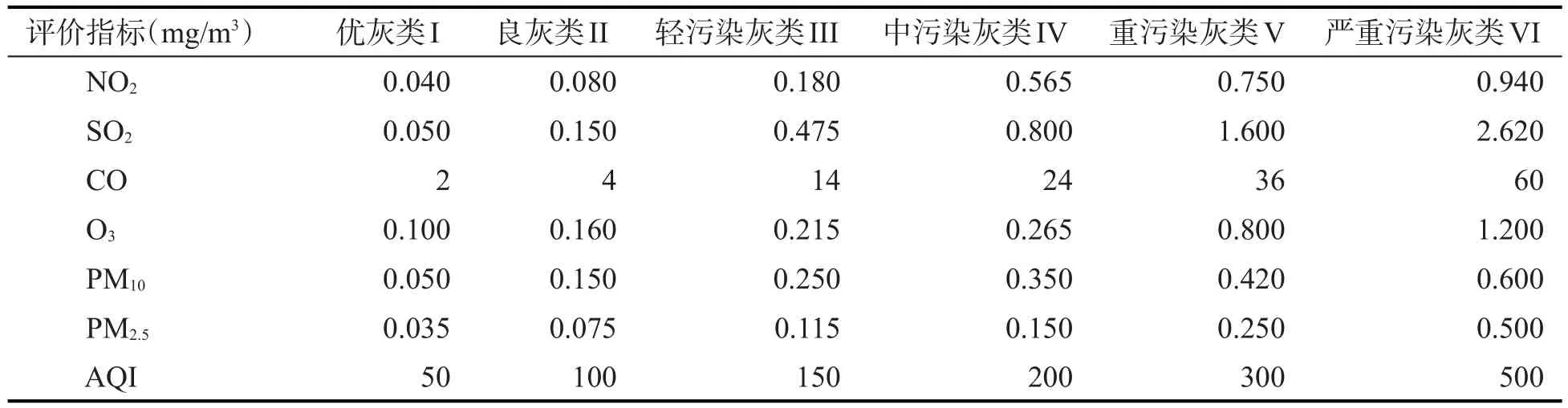
表1 灰类的划分标准

合肥市从2015年开始采用AQI指标评价空气质量，所以选取2015年1月至2018年2月合肥市城市空气质量日数据共1 155条作为聚类样本进行实例评价。原始监测数据经过处理单位统一为mg/m3，并从此样本数据中随机提取部分数据如表2所示。

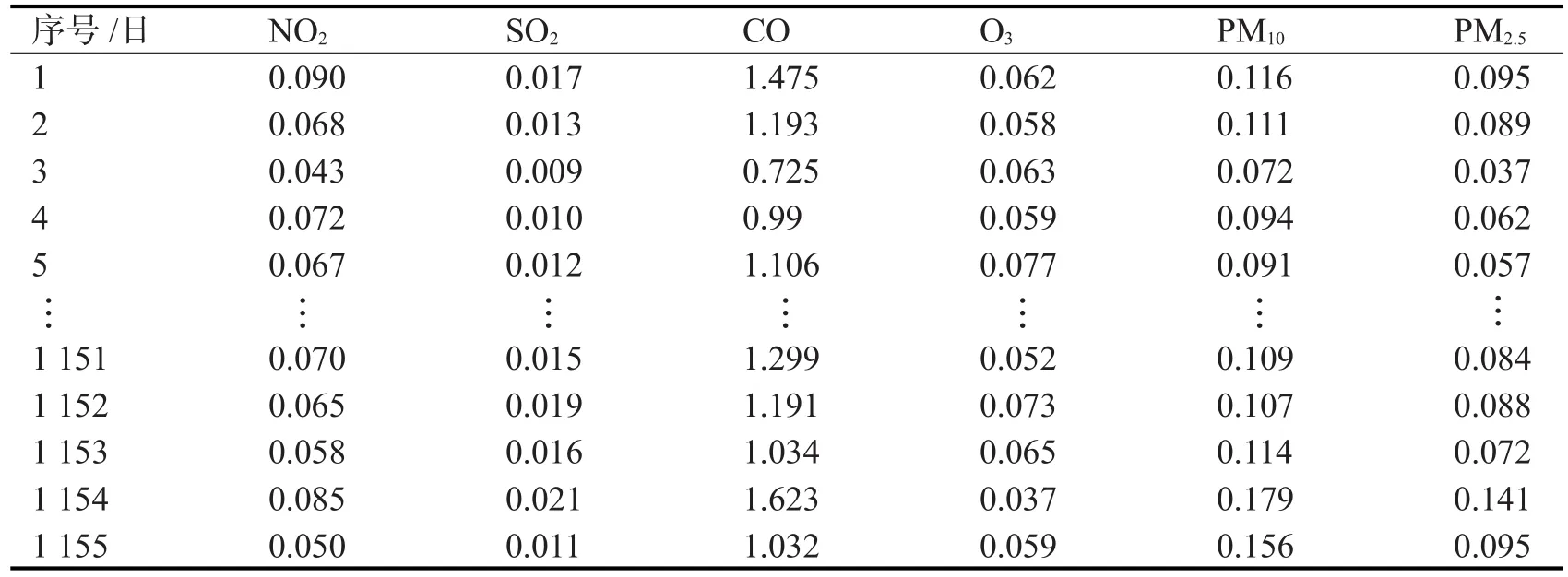
表2 合肥市空气质量监测数据（部分样本）

1.3 数据的标准化处理

为了使聚类样本的计算和综合分析变得简单，先需要消除维数的影响，因此对聚类样本的白化数进行归一无量纲化处理=xij/Soj，其中是样本归一化的结果，xij是第i个聚类样本的第j个聚类索引的检测数据，Soj为指标限值的平均值，作为参考标准值。表3显示了标准化样本数据的结果。

表3 标准化处理后的样本

表4 标准化处理的灰度限值

1.4 确定白化函数

本文评价的空气质量基于划分的直线型梯形白化函数，上限及下限白化函数分别用于描述I、VI等级，中间Ⅱ、Ⅲ、IV、V等4个等级分别用典型级别白化函数描述。灰类的区间范围即每个浓度等级范围对应一个质量评价等级，在此范围内白化值都为1。基于构建评估指标的灰阶白化函数，获得灰阶白值，其中x是白化数中的实际指标。为节省篇幅，本文仅以PM2.5指标为代表，具体白化函数如下。

1.5 聚类权重的确定

经典灰色聚类模型主要分析目标的指标权重和实际权重。指标权重主要考虑各类指标在空气质量评价中的权重。灰类限值越大，指标权重在同一灰类中所占权重越大，这将导致聚类对象的该指标的数值相对于其他指标数值偏大。指标在整个评价体系中的重要性并不相同，因此应该考虑评价指标实际权重，而实际样本数据的权重未表现在白化函数中，因此对实际样本数据和评价指标权重叠加计算，突出样本权重，评估结果将会倾向于采样数据级别，并选择权重最高的指标污染物作为主要污染物。下面将分别给出指标权系数和实际权的定义和公式。

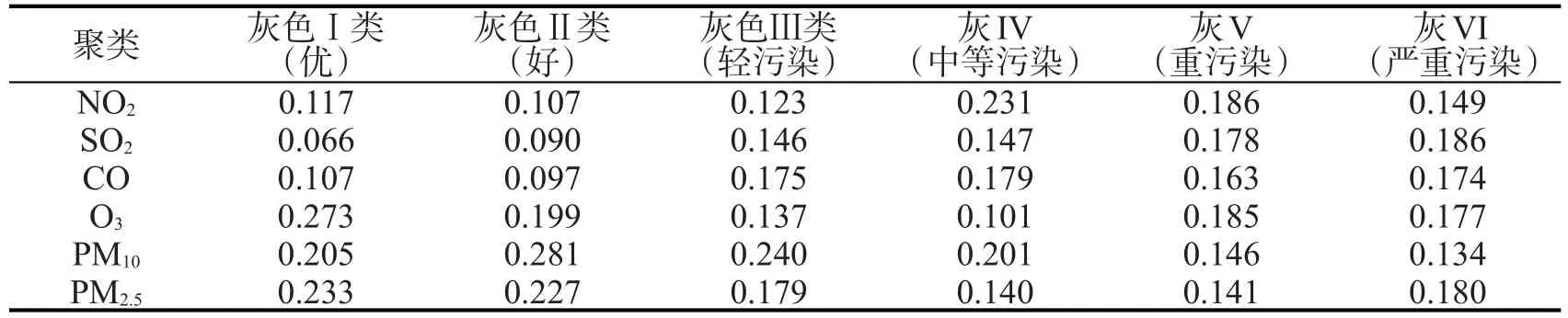
表5 指标灰色聚类权

1.6 计算灰色聚类系数

将标准化的实际指标值代入白化函数，乘以指数权重，再乘以实际权重，计算第i个聚类对象的第k个灰色聚类的聚类系数由每个聚类对象的6个聚类系数级别组成，选取表3样本数据中前5条和后5条数据，求出聚类系数矩阵，以上计算过程较复杂，通过MATLAB编程实现。令δ*=max1≤k≤s{}，则其对应的灰类等级即当日空气质量级别，如表6所示。

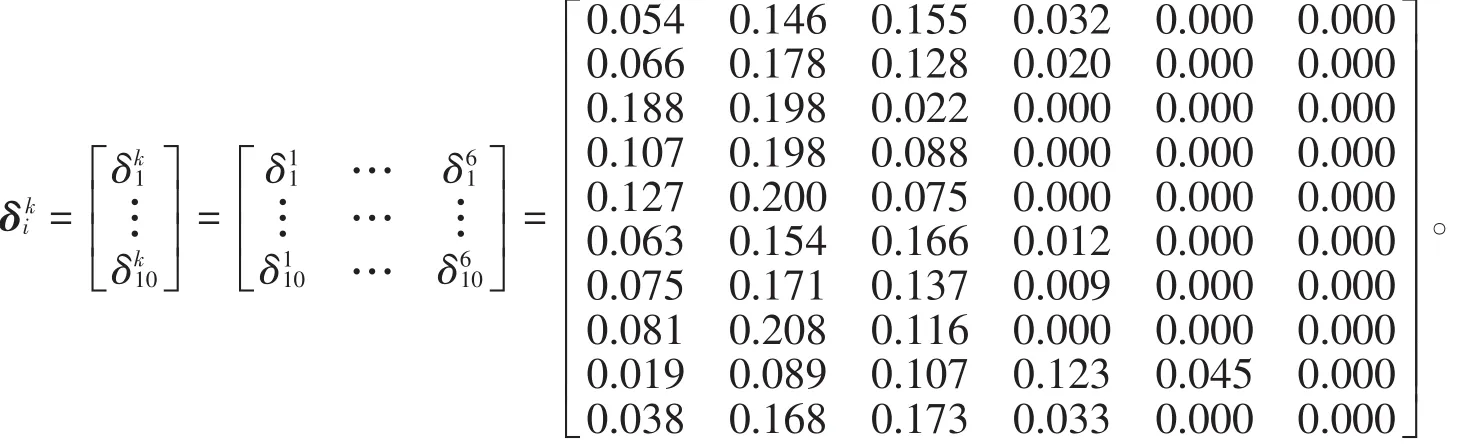
表6 聚类系数矩阵结果

2 评价结果分析对比

从2015年1月至2018年2月合肥市城市空气质量日数据中随机选取1 155条空气质量数据，利用灰色聚类模型评价出每天的空气质量等级。为了验证改进的灰色聚类法评价结果的准确性和可靠性，将评价结果与模糊综合评价法以及我国大多数城市采用的AQI方法进行比较。样本数据的灰色聚类、模糊综合评价法以及AQI评价等级如表7所示。从表7中可以看出，灰色聚类方法与模糊综合评价法评价的结果有一定的差异，与AQI评价结果也存在差异。

表7 3种评价法评价结果对比

灰色聚类评价方法与AQI评价的系数、等级和首要污染物结果对比如表8所示。空气质量等级的两种评价结果基本相同，而利用灰色聚类模型确定的首要污染物全部是细颗粒物，只包括PM10和PM2.5，并且绝大部分的首要污染物是PM2.5。在AQI方法评价的结果中4和5的首要污染物是NO2，这一点两种评价方法存在差异。

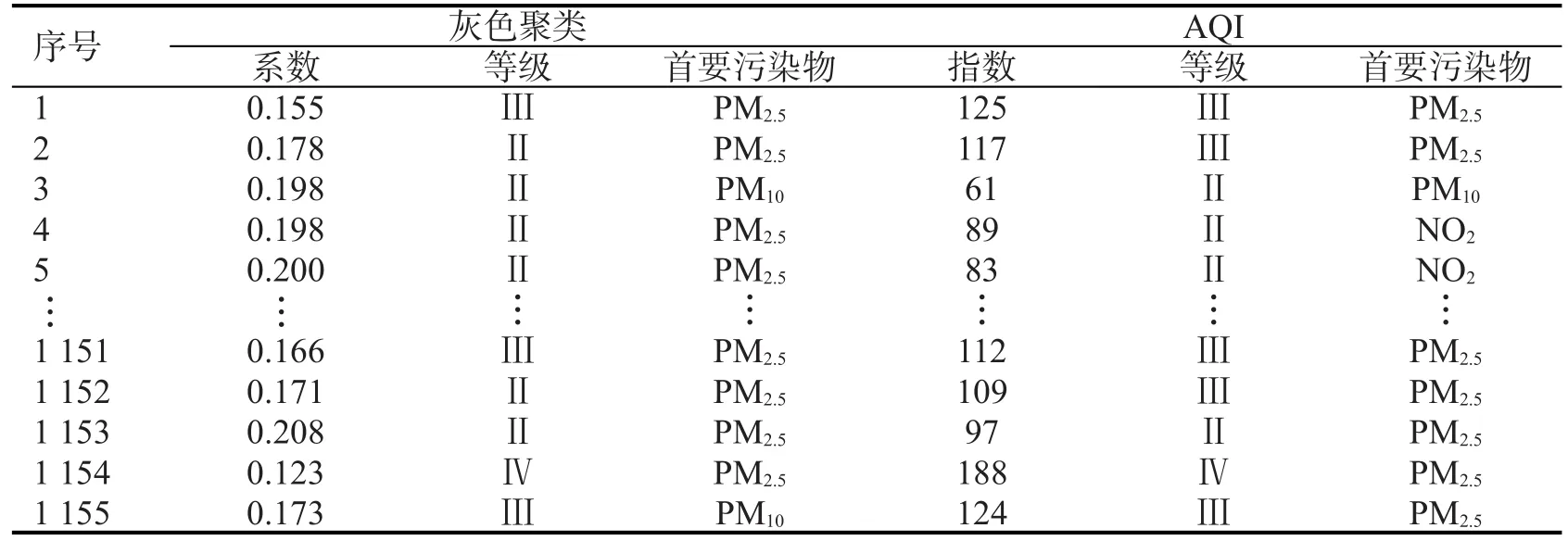
表8 评价结果比较

灰色聚类评价过程中综合考虑指标权和实际权的叠加权重，使得评价结果与真实的空气质量状况基本相匹配。采用AQI方法仅能粗略地评价空气污染的质量等级，使得监测数据处理后的结果不是特别准确。灰色聚类考虑到空气中的污染因素及污染数据的不确定性和随机性，对数据的处理全部采用精确化数字结果，使得该模型的评判结果趋于准确和稳定。在AQI方法中更偏向于采用最主要的污染因子进行研究，且监测数据不多。如果总是以最大的污染因子数据进行分析，会使数据处理的结果有比较大的误差，容易产生边界性问题，且评价结果相对不准确。 灰色聚类评价模型考虑了各项指标的实际权重，克服了AQI评价中以最大污染指标代替整体指标的不足和模糊综合评判法不确定的最大隶属函数问题。

3 结束语

本文通过改进灰色聚类模型评价方法，利用多种污染物指标评价合肥市2015年1月至2018年2月空气质量状况。文章通过提取部分样本数据后被标准化并确定白化函数，利用叠加权重计算出聚类系数，将评价结果与模糊综合评价法和AQI评价结果作比较，可以看出该模型评价结果与实际情况匹配更好，有效地解决了以单一的污染指标代替总体而存在的模糊性问题，同时运用白化函数进行数据处理，解决了评价等级的边界性问题。

空气的化学成分复杂，传统等比例灰色聚类模型的评价因子数值会过于离散化，数据处理会更加复杂化，从而遗漏许多关键性信息。为了提高评价结果的准确性，在以后的研究中要优化评价模型，采用指数型白化函数来代替传统等比例函数模型，以更准确地评判城市环境质量。