预给极点的二元连分式插值

胡 枫

(安徽理工大学数学与大数据学院，安徽淮南232001)

自然科学与工程计算中经常需要处理带有极点的奇异值函数，而避免极点的出现和控制极点的位置一直都是有理插值与逼近理论中的热点问题。通过选择特殊的权函数，Berrut提出了一种无极点的重心有理插值[1]；Schneider等在文献[2]中给出了重心有理插值无极点时，相邻权系数异号这一必要条件，进而研究了相邻权系数同号时，插值函数在每个子区间拥有奇数个极点的情形；Foater等通过局部混合，建立了一族没有极点且能达到任意逼近效果的重心插值函数[3-4]。但在实际工程计算中，常常要利用极点来解决实际应用。因此，朱功勤等在已知极点信息的情形下对预给极点的连分式插值和向量值插值进行了深入的研究[5]。关于二元有理插值函数的研究，前人已做出了大量的贡献[6-10]，本文研究预给极点的二元连分式插值，将原有节点的函数值乘以一个确定的数，使其变成一个无预给极点的二元有理插值问题。通过计算具有继承性的系数来构造一种二元连分式插值新算法，再除以带有极点信息的函数，从而得到预给极点的二元有理插值函数。本文使用的方法在保持原有每个极点的重数不变的同时又能更好地区分预给极点的位置，并通过数值例子验证了该方法的有效性和合理性。

1 二元连分式插值

Michalik为了求解非线性方程提出了一种新的连分式形式[11]，本文对其进行二元推广，设点集Dn={(x0,y0),(x1,y1),…,(xn,yn)}⊂ [ a ,b ] ×[ c ,d ]，函数z=f(x,y)对应的函数值为zi=f(xi,yi)，i=0,1,…,n。当且仅当i=j时，xi=xj，yi=yj，i=0,1,…,n，Dn上的二元连分式插值形式为

其中ck=ck(x0,x1,…,xk;y0,y1,…,yk) ，k=0,1,…,n是具有继承性的系数，计算过程如下所示：

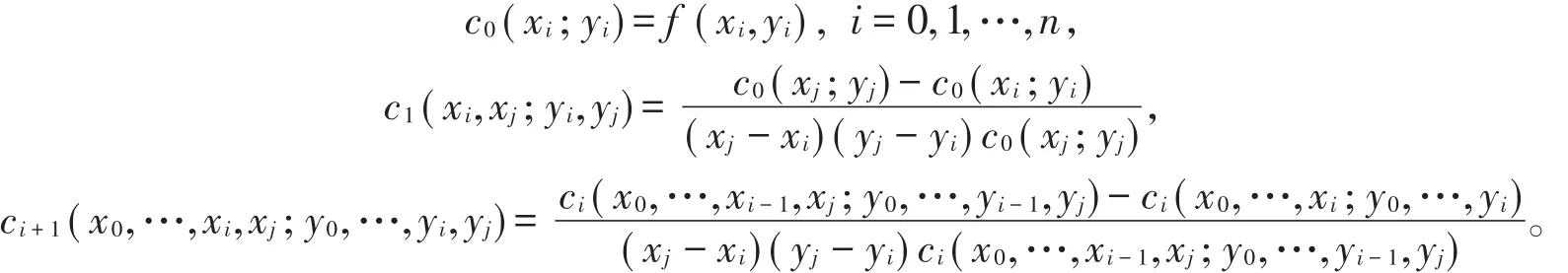
从插值函数的最后一项开始计算，容易验证(1)式满足所有插值条件，即插值函数通过所有的插值节点(xi,yi)(0≤i≤n)，为了更好地描述上述系数的计算过程，现归纳为如表1所示。

表1 二元连分式系数的计算过程

下面讨论该二元连分式插值的一些重要性质。

性质1二元连分式插值的三项递推公式。对二元连分式插值函数，设P-1=1，P0=b0=0，Q-1=0，Q0=1，则对于n ≥ 1有

性质2特征定理。由于二元多项式C(x,y)=cijxiyj的次数有两种不同的定义，下面从两个角度分别给出二元连分式插值的特征定理。

(1) 分别定义变量x和y的次数，即∂Cx={i}，∂Cy={j}，则当n=k，k=0,1,…，

性质3二元连分式插值不可达点的修正处理方法。定义在数据点集Dn上的二元连分式插值，若Pn(xi,yi)-Qn(xi,yi)fi=0，≠ fi，i=0,1,…,n，则称(xi,yi)是插值函数Rn(x,y)的不可达点。

在文献[12]中提出了一种对不可达点的修正处理方法，现设Rn(x,y)有l个不可达点，通过调整节点的顺序使这些不可达点位于插值节点的后l位，构成新的插值点集

令

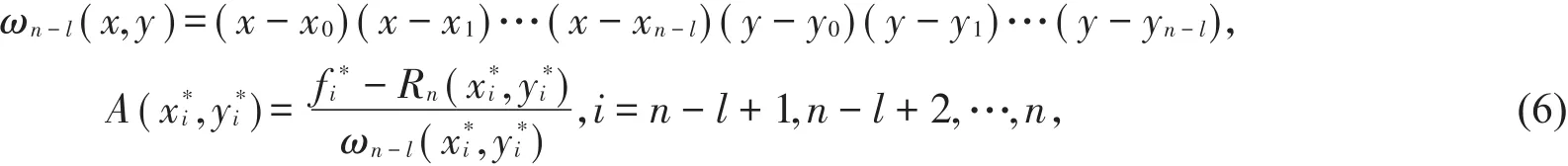
2 预给极点的二元连分式插值

通过计算具有继承性的系数ck(0≤k≤n)，构造满足条件(7)式的二元连分式插值Gn(x,y)，从而得到预给极点的二元连分式插值函数。显然当Gn(x,y)的分子和分母中各项多项式在预给极点处都不等于零时，二元插值函数rn(x,y)具有预给的极点且极点的重数不发生变化，进一步在第二种情形下考虑二元多项式的次数，当n是偶数，rn(x,y)是[ n ] [n +2p ]型，当n是奇数，rn(x,y)是[ n -1 ] [ n +1+2p]型的有理插值函数。

3 数值例子

(7)式得到相应的无预给极点的插值函数，对应数据如表3所示。

表2 插值数据

表3 无预给极点的插值数据

根据表3和上文中系数ck的递推算法，得到无预给极点的二元连分式插值函数Gi(x,y)及相应的ri(x,y)，i=3，4，5。

下面使用Matlab2014a分别绘出各个预给极点插值函数ri(x,y)和误差函数ei(x,y)=f(x,y)-ri(x,y)，i=3,4,5的部分图像，如图1～6所示。

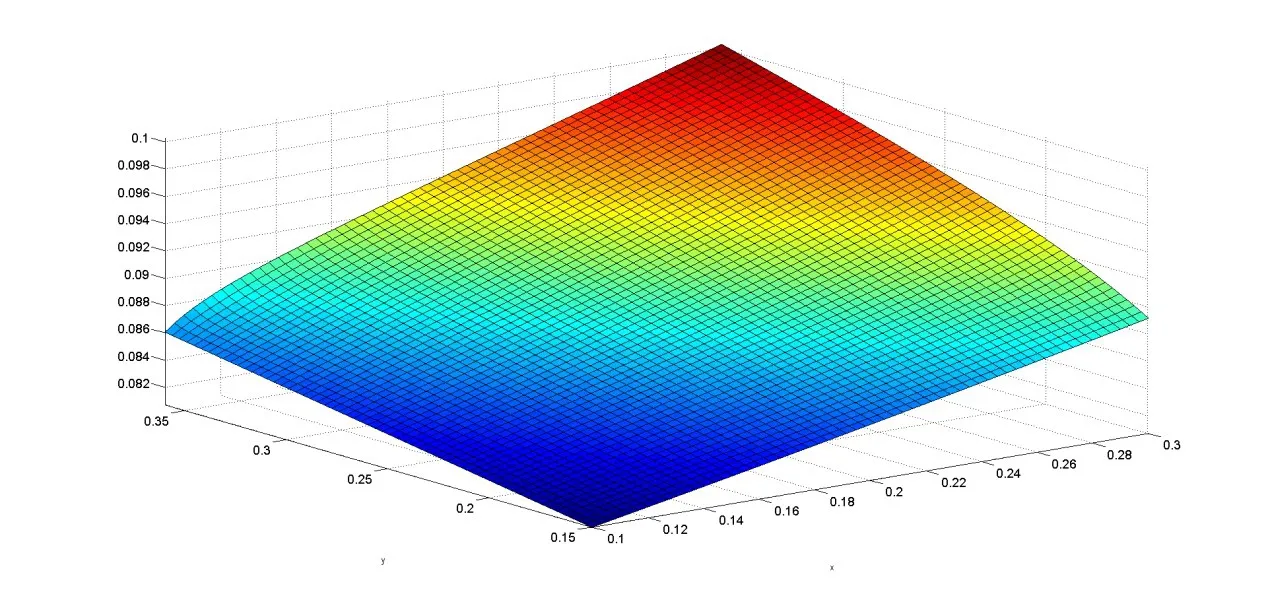
图1 r3(x,y)在[0.1,0.3]×[0.15,0.35]上的部分图像

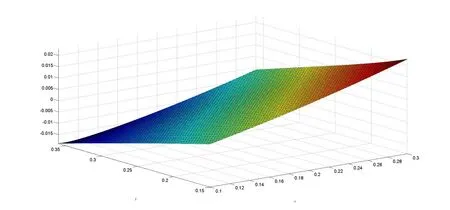
图2 e3(x,y)在[0.1,0.3]×[0.15,0.35]上的部分图像

图3 r4(x,y)在[0.3,0.5]×[0.35,0.55]上的部分图像

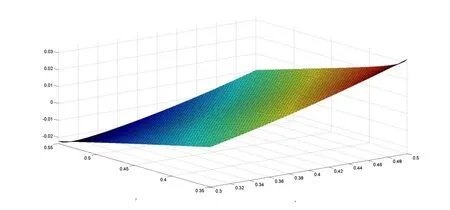
图4 e4(x,y)在[0.3,0.5]×[0.35,0.55]上的部分图像

图5 r5(x,y)在[0.45,0.6]×[0.46,0.65]上的部分图像

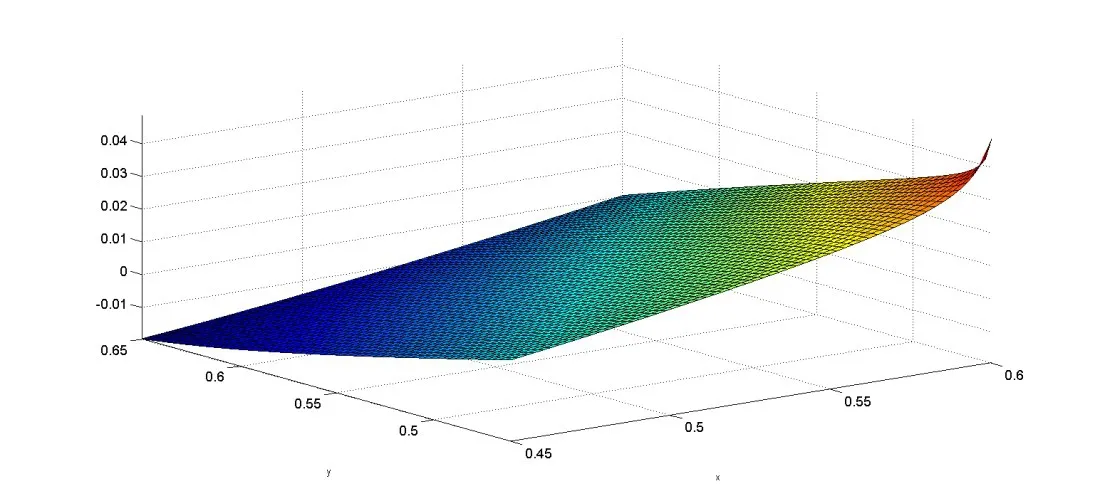
图6 e5(x,y)在[0.45,0.6]×[0.46,0.65]上的部分图像

4 结论

本文研究预给极点的二元连分式插值，由预给极点的信息，使每个原函数值乘上一个确定的数，通过文中提及的新的二元连分式插值算法来构造一个无预给极点的插值函数，再除以一个带有预给极点信息的函数，从而得到预给极点的二元连分式插值。该方法获得的插值函数在保持原有每个极点的重数不变的同时，又能更好地区分预给极点的位置。给出的数值实例很好地验证了文中理论的有效性和合理性。