Nd、N掺杂ZnO的电子结构和光学性质的第一性原理研究

刘丹枫， 赵 璨， 刘桂安， 雷博程， 夏 桐， 黄以能, 2， 张丽丽, 2

(1.伊犁师范学院 物理科学与技术分院 新疆凝聚态相变与微结构实验室，伊宁 835000； 2.南京大学 物理学院 国家固体微结构重点实验室， 南京 210093)

1 引 言

ZnO是一种应用前景十分广泛的宽带隙半导体材料，在室温下的禁带宽度达到3.37eV，激子结合能为60 meV[1]. 由于ZnO具有无毒无污染、原料丰富易得、制备成本低、热稳定性、气敏性、压敏性、导电性等优点[2,3]，所以在光电、铁磁、薄膜制备等诸多方面都有潜在的应用前景[4-7]. 近年来大家主要采用掺杂不同类型的元素对ZnO进行光电改性[8-12]，来制作ZnO薄膜光电器件.

余长林等人[13]研究了Ag掺杂ZnO体系，发现Ag掺杂ZnO可以引起光吸收边一定程度的红移，提高光的催化活性；崔红卫等人[14]研究了Sn掺杂ZnO电子结构与光学性质，计算结果表明：随着掺杂Sn浓度的增加，光学吸收带边发生红移，红移程度随着掺杂浓度的增加先减弱后增强，表明Sn掺杂ZnO是一种良好的透明导电氧化物薄膜材料；韩伟超等人[15]研究了S掺杂纤锌矿ZnO的光催化性质，结果表明：S掺杂后吸收谱出现红移，且吸收谱峰值随掺杂量的增加而增大，提高了可见光和紫外光区域的光吸收. 除此，由于稀土元素具有独特的最外层电子结构，现已被广泛运用于电磁器件和发光材料的生产中，越来越多的研究者开始研究稀土元素掺杂ZnO，李泓霖等人[16, 17]研究稀土元素Er和Gd掺杂ZnO体系时发现Er和Gd掺杂ZnO在可见光区的吸收系数和反射率都有变大，且能量损失峰出现红移现象；在研究Eu掺杂ZnO结构的光电性质时发现纯净的ZnO与掺杂Eu后相比，介电函数虚部有明显的差异，低能部分的峰位随着掺杂量的增加介电函数虚部会出现红移现象，可见光区的吸收系数变大；李聪等人[18]研究了La掺杂量对ZnO光电性能影响，计算结果表明：通过控制La浓度与掺杂方式可以有效提高ZnO对可见光的吸收系数，使光生空穴-电子对有效分离产生影响；韦建松等人[19]研究掺杂Nd对ZnO电子结构和光学性质的影响发现Nd掺杂所引起的介电函数变化对研究基于ZnO的新型光电功能材料具有重要的指导意义.

所以，ZnO掺杂各种类型元素的理论及实验研究已成为该领域的一个研究热点，并且通过掺杂这种方式能够使人们对ZnO掺杂结构的光电性质的变化机理有一个新的认识[20-24]. 本文以ZnO作为基体，非金属N元素和稀土元素Nd作为掺杂原子，利用第一性原理超软赝势方法，对ZnO掺杂N元素和Nd元素前后晶体的形成能、能带、电子态密度和光学性质进行了对比研究，初步揭示了通过ZnO掺杂稀土元素改变光电性质的内在原因，为实验工作提供理论参考.

2 计算方法及模型

基于Kohn-Sham自洽密度泛函理论的第一性原理的方法，利用Material Studio中的CASTEP[25]软件完成，在搭建模型时进行了几何优化，计算中选用GGA+U[26-29]的超软赝势和PW91交换关联函数，计算过程中，Zn的3d电子加U值是8.12，O的2p电子加U值是4.64，平面波截断能取360 eV，布里渊区K点值为2×2×2，自洽精度为2×10-5eV/atom，晶格常数为a=b=3.257 Å，c=5.2016 Å，空间点群为P63m(No.186)，建立ZnO晶胞2x2x1超胞模型如图1(a)所示，使用原子替代法，即用一个N原子替代一个O原子，一个Nd原子替代一个Zn原子，这个模型用ZnO-N-1Nd表示，如图1(b)；用一个N原子替代一个O原子，两个Nd原子替代两个Zn原子，这个模型用ZnO-N-2Nd表示，如图1(c)；用一个N原子替代一个O原子，三个Nd原子替代三个Zn原子，这个模型用ZnO-N-3Nd表示，如图1(d)；ZnO单掺N原子时，是用一个N原子替代一个O原子，这个模型用ZnO-N表示，如图1(e). ZnO单掺Nd原子时，是用一个Nd原子替代一个Zn原子，这个模型用ZnO-Nd表示，如图1(f).

3 计算结果与讨论

3.1 Nd与N共掺杂ZnO掺杂前后的晶体结构

表1为纯ZnO、ZnO-N-1Nd共掺体系、ZnO-N-2Nd共掺体系以及ZnO-N-3Nd共掺体系和ZnO-N，ZnO-Nd几何优化后体系的总能量，形成能，键布居，以及键长. 形成能(EΔ)表示掺杂形成的难易程度，其值越正，表示不容易形成，其值越负，表示杂质越容易掺杂进入，其公式如下[30].

EΔ=EZnO:N/Nd-EZnO-nEN-mENd+nEO+mEZn

(1)

公式中EZnO:N/Nd与EZnO分别表示N、Nd原子掺杂前后的总能量，EN、ENd、EO、EZn分别表示N、Nd、

图1 掺杂前后晶胞结构图 Fig. 1 Crystal cell structure before and after doping

O、Zn原子的基态能量，n，m分别表示掺入的杂质原子的个数和被替代原子的个数. 由表1EΔ的数据可知单掺杂的形成能比共掺的大，说明共掺体系更容易形成，并且共掺体系有随掺杂浓度增加，其形成难度升高的趋势，说明低浓度掺杂更容易形成.

键布居数为正，数值越大其共价性越强，若其值为负，数值越小其离子性越强. 由Zn-O键布居数据可知，最大与最小Zn-O键长布居数由单掺到共掺，并随共掺杂质浓度升高而变强，表明其共价性也是这样变化，并且这个变化趋势与形成能正比，说明Zn-O键的共价性的强弱与杂质掺入浓度成正比.

由最大及最小Zn-O键长数据，可知，它们都是由单掺到共掺随着共掺浓度而减小，同一体系最大与最小的差值，共掺体系的比单掺体系的大，证明共掺体系发生了较强的畸变，这是因为RNd(2.64 Å)>RZn(1.53 Å)，RN(0.75 Å)>RO(0.65 Å)，并且随着掺杂浓度的升高，其畸变的强度就越强，这将导致ZnO原有的晶体对称性被破坏，正负电荷中心不再重合，而产生局域电势差，有利于阻碍光生空穴和电子对的复合，进而有望提高材料的光催化性能.

表1 各模型的能量，形成能，键布居数，与键长

3.2 能带结构和态密度分析

3.2.1Nd、N单掺ZnO掺杂前后的能带结构和态密度分析

图2是纯ZnO的能带结构图，图中的G、F、Q、Z、G为布里渊区高对称点，计算得到纯ZnO的禁带宽度为3.375 eV，大于实验值0.005 eV，本实验得到的结果与实验值的差距较小，故计算所选取的参数设置是可靠的. 因为结构的性质主要由费米能级附近这部分所决定，图2(a)给出了-10—10 eV部分的能带结构，从图中可看出导带底位于布里渊区G点，价带顶位于布里渊区G点，说明ZnO是直接带隙半导体. 图3(a)是纯ZnO态密度图，从图中可以看出，纯ZnO的价带主要是由Zn的3d态和O的2p态贡献，导带主要由Zn的4s态贡献，所以ZnO既有离子键又有共价键.

图2(b-c)分别是ZnO-N掺杂体系和ZnO-Nd掺杂体系的能带结构图，与未掺杂ZnO体系比较，跃迁类型未改变，都是直接跃迁，但是禁带宽度明显减小，分别降低到1.93 eV和0.069 eV，掺杂原子是禁带变小的主要原因. ZnO-N掺杂体系出现了杂质能级. 结合图2-3可以知道ZnO-N掺杂体系的杂质能级主要是由N的2p态贡献.

图2 掺杂前后ZnO能带结构图: (a) ZnO; (b) ZnO-N; (c) ZnO-NdFig. 2 ZnO band structure before and after doping: (a) ZnO; (b) ZnO-N; (c) ZnO-Nd

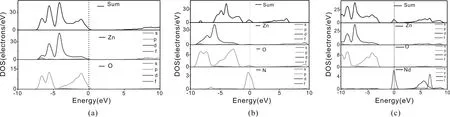
图3 掺杂前后ZnO体系态密度: (a) ZnO; (b) ZnO-N; (c) ZnO- NdFig. 3 ZnO state density before and after doping: (a) ZnO; (b) ZnO-N; (c); ZnO- Nd

3.2.2Nd、N共掺ZnO的能带结构和态密度分析

图4(a-c)是N、Nd共掺ZnO体系能带结构图，从图中可知ZnO-N-1Nd掺杂体系，其跃迁类型是直接跃迁，其禁带宽度是0.262 eV；ZnO-N-2Nd掺杂体系，其跃迁类型是间接跃迁，禁带宽度是0.196 eV；ZnO-N-3Nd掺杂体系，其跃迁类型是间接跃迁，禁带宽度是0.218 eV，同样掺杂原子是禁带变小的主要原因. N、Nd共掺ZnO体系都产生了能级分裂，结合图5(a-c)可知ZnO-N-1Nd掺杂体系，杂质能级主要由N的2p态和Nd的4f态贡献；ZnO-N-2Nd掺杂体系杂质能级主要是由N的2p态和Nd的4f态贡献；ZnO-N-3Nd掺杂体系杂质能级主要是由Nd的4f态贡献，随着Nd的掺杂个数增加，导带底下移，使费米能级穿过导带，呈N型半导体特征，这是由于稀土元素的掺入使得导电载流子增多引起的. 其中ZnO-N-2Nd掺杂体系，禁带宽度值最小. 结合图2-图5可知掺杂体系相比纯ZnO体系，掺杂后禁带宽度变窄，电子跃迁到导带上所需的能量更小，导电性能有所增强，扩大了对可见光的响应范围，也将提高材料的光催化功能.

图4 N、Nd共掺ZnO体系能带结构图: (a) ZnO-N-1Nd; (b) ZnO-N-2Nd; (c) ZnO-N-3NdFig. 4 The energy band structure of ZnO system is doped jointly by N and Nd: (a) ZnO-N-1Nd; (b) ZnO-N-2Nd; (c) ZnO-N-3Nd

图5 N、Nd共掺ZnO体系态密度: (a) ZnO-N-1Nd; (b) ZnO-N-2Nd; (c) ZnO-N-3NdFig. 5 State density of ZnO system is doped jointly by N and Nd: (a) ZnO-N-1Nd; (b) ZnO-N-2Nd; (c) ZnO-N-3Nd

3.3 Nd与N共掺杂ZnO掺杂前后的光学性质

图6(a)是ZnO掺杂前后的吸收光谱. 纯ZnO体系、ZnO-N掺杂体系、ZnO-Nd掺杂体系的光吸收边分别为3.193 eV、0.136 eV、0.204 eV，对比可得，ZnO-N掺杂体系光吸收边红移较大. ZnO-N-1Nd掺杂体系、ZnO-N-2Nd掺杂体系、ZnO-N-3Nd掺杂体系的光吸收边分别为0.238 eV、0.170 eV、0.126 eV，对比发现随着掺杂浓度的增大，体系红移的幅度也增大，这是因为随着掺Nd的个数的增多，掺杂体系的禁带宽度减小程度越大所引起的，当禁带宽度越小，电子越容易从价带激发到导带，减小了所需的电子能量，从而诱发了吸收光谱边缘发生红移现象，掺杂后体系在可见光区的吸收系数也随着浓度的增加而增加.

对比掺杂前后的吸收峰发现，在N、Nd共掺ZnO体系中，随着掺杂Nd的个数增加，吸收峰个数明显增多，则激发态的价带电子向导带跃迁的过程几率也增大. 并且可以明显看出对比纯ZnO的光吸收边，掺杂后的光吸收边都向低能方向移动，发生红移. 从图6(b)可见光区域中可知掺杂体系的响应范围扩展到可见光范围，其中ZnO-N-3Nd掺杂体系在可见光区域里吸收系数最大，光催化性最强.

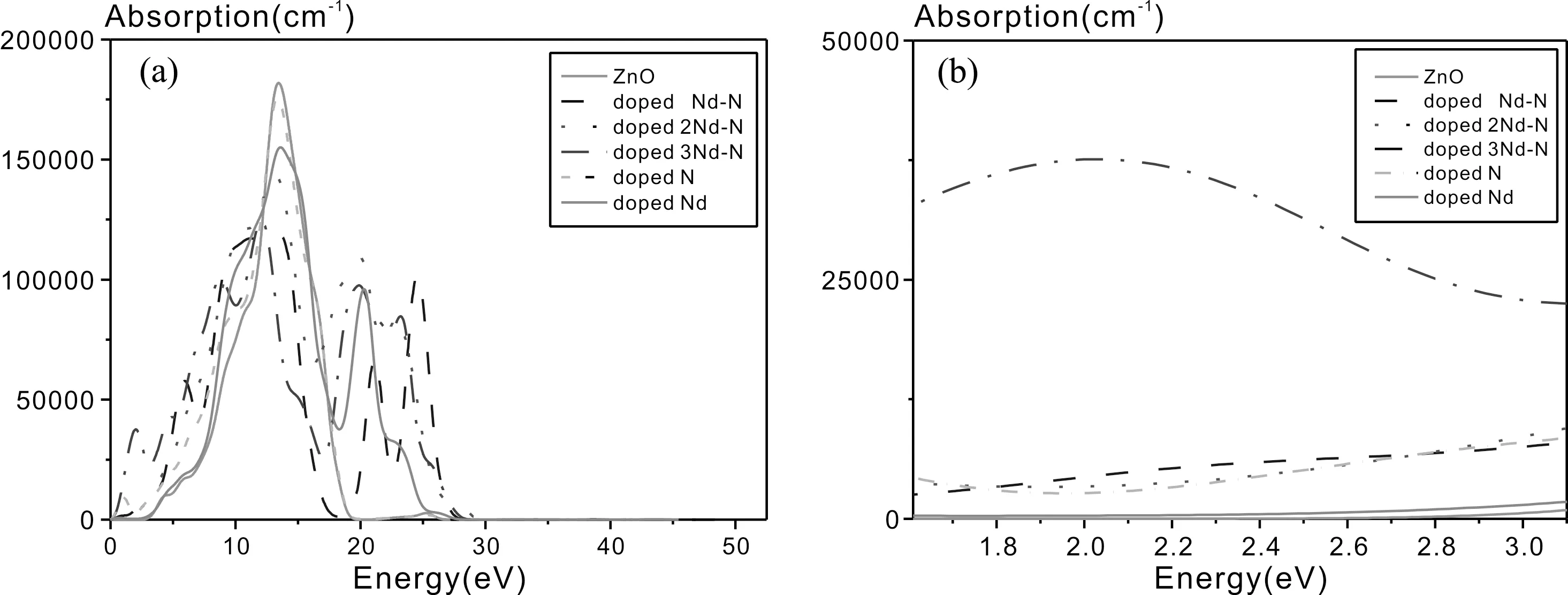
图6 光学性质图: (a) 吸收谱; (b) 可见光区域吸收谱Fig. 6 Optical properties: (a) absorption spectrum; (b) visible region absorption spectrum

图7(a)是ZnO掺杂前后的介电函数的实部曲线图，其对应介电常数随入射光能量的变化. 介电常数表征了介质在外电场作用下极化程度，也就是对电荷的束缚能力，介电常数越大，对电荷的束缚能力越强. 在无入射光情况下，介电函数的实部对应的纵坐标是静态介电常数，从图中可以得到纯ZnO的静态介电常数值为1.874，随着光子能量的增加，在3.595 eV位置形成一个小峰，紧接着在5.840 eV处也形成了峰值.

ZnO-N掺杂体系、ZnO-Nd掺杂体系、ZnO-N-1Nd掺杂体系、在ZnO-N-2Nd掺杂体系、在ZnO-N-3Nd掺杂体系的静态介电常数值分别为6.704、2.704、3.365、5.370、9.518. 单掺N的静介电常数比单掺Nd的大，各共掺ZnO体系，随着掺杂Nd的浓度增加，静介电常数也增加. ZnO-N掺杂体系在11.679 eV处形成一个小峰；ZnO-Nd掺杂体系在3.782 eV处形成一个小峰；ZnO-N-1Nd掺杂体系在1.743 eV、4.621 eV、7.801 eV处形成了峰值；ZnO-N-2Nd掺杂体系在3.057 eV、5.276 eV处形成了峰值；ZnO-N-3Nd掺杂体系2.559 eV、7.671 eV处形成了峰值. 由此可知，N、Nd共掺ZnO体系的极化能力较强，据此可推测共掺体系的光生电场强度较大，会使光激发载流子在晶体内的迁移变快，对电荷的束缚能力增强.

图7(b)是纯ZnO和Nd与N共掺杂ZnO体系介电函数的虚部曲线图，对应了ZnO各体系不同轨道的电子在各能带之间的带间跃迁. 从图中可得纯ZnO曲线两个主要峰分别在12.768 eV和4.261 eV. ZnO-N掺杂体系的曲线三个主峰位于0.567 eV、8.945 eV、12.741 eV处. ZnO-Nd掺杂体系的曲线三个主峰位于9.361 eV、12.778 eV、20.097 eV处. 在ZnO-N-1Nd掺杂体系，形成了五个峰，分别位于0.570 eV、5.507 eV、8.791 eV、21.107 eV、24.391 eV处. 在ZnO-N-2Nd掺杂体系，形成了四个峰，分别位于0.585 eV、9.369 eV、18.152 eV、23.038 eV处在ZnO-N-3Nd掺杂体系，形成了六个峰，分别位于0.420 eV、5.332 eV、8.791 eV、12.474 eV、18.222 eV、23.089 eV处.

图7 光学性质图: (a) 介电函数实部图; (b) 介电函数虚部图Fig. 7 Optical properties: (a) The real part of the dielectric function; (b) The imaginary part of the dielectric function

4 结 论

本文主要是应用基于密度泛函的第一性原理计算ZnO的电子结构，进行计算的软件为Material Studio 8.0中的CASTEP模块. 经系统的计算本征和掺杂ZnO的电子结构，包括能带结构、态密度、分波态密度、吸收谱、介电函数等，并对其进行了一定分析，分析得到主要结果如下：

(1)N、Nd掺杂ZnO，其单掺杂的形成能比共掺的大，说明共掺体系更容易形成，并且共掺体系有随掺杂浓度增加其形成难度升高的趋势，说明低浓度掺杂更容易形成. 随着掺杂浓度的升高，其畸变的强度就越强，这将导致ZnO原有的晶体对称性被破坏，正负电荷中心不再重合，而产生局域电势差，有利于阻碍光生空穴和电子对的复合，进而有望提高材料的光催化性能.

(2)掺杂后，禁带宽度都减小，其中掺杂Nd原子时，禁带宽度最小为0.069 eV. N、Nd共掺ZnO体系，ZnO-N-2Nd掺杂体系的禁带宽度值最小. 掺杂后禁带宽度变窄，电子跃迁到导带上所需的能量更小，可增加对可见光的响应范围. 杂质能级主要由Nd的4f态和N的2p态贡献，从而增加掺杂ZnO载流子浓度，使ZnO呈N型半导体特征.

(3)在光学性质分析中，N、Nd共掺ZnO体系的吸收系数较大，并且都产生了红移，光谱相应范围扩展到了可见光的全部吸收范围，将提升材料的光催化性. N、Nd共掺ZnO体系的低能区域的介电谱峰值较高，说明其极化能力较强，光生电场强度较大，会使光激发载流子在晶体内的迁移变快，对电荷的束缚能力增强.