基于投影的点云配准算法
江 盟 ,蔡 勇,张建生
(1.西南科技大学制造科学与工程学院,四川 绵阳 621010;2.制造过程测试技术省部共建教育部重点实验室,四川 绵阳 621010)
0 引言
点云配准技术是逆向工程和产品检测中非常重要的环节。目前,点云自动配准算法中应用广泛的是迭代最近点(iterative closest point,ICP)算法及其改进算法[1]。配准点云的初始位置是ICP算法非常重要的限制条件。该条件影响ICP算法的配准速度和全局收敛。粗配准技术能有效解决ICP算法对初始配准位置的要求。文献[2]在逆向工程中,将多次扫描得到的点云数据先采用主成分分析(principal component analysis,PCA)粗配准,再采用ICP算法实现精细化配准。PCA算法的特点是粗配准速度非常快,但鲁棒性很差。为增强粗配准的鲁棒性,文献[3]利用二维图像提取特征点实现点云配准,但提取特征的过程相当耗时,且噪声对算法的影响比较大。
点云配准本质是求优化解的过程[4]。其中比较重要的两个问题是:第一,设计一个可行的评价函数;第二,采用一种有效的搜索方法[5-7]。评价函数有空间分布熵[5]、表面融合[7]等。遗传算法对于多变量多目标的问题求解具有非常好的效果,因此许多学者在点云配准中使用遗传算法作为搜索方法[8-10]。此外,将随机抽样一致性算法引入点云配准[11-12],也能达到很好的配准效果,但是其配准速度比较慢。
本文提出了一种降维处理点云数据的配准算法。首先,将配准点云投影到三个坐标平面,并且划分平面以统计每一个格子中的点数;然后,分别求解每个投影平面的熵值,再利用遗传算法来搜索使得三个投影平面熵值和最小的空间变换矩阵;最后,将最优矩阵作用于目标点云,实现配准。
1 点云空间位置关系评价
快速、精确地评价点云的空间位置,是点云配准中非常重要的环节。本文将点云数据的三维立体图形经过投影降低维度到二维,再经过统计计算来评价两片点云的空间位置关系。
1.1 信息熵的定义
对于包含N个点的点云P,将其投影到某平面得到二维投影点云P’。将投影平面的横坐标和纵坐标均按间隔ΔL进行栅格化,统计输入点云数据的总点数N及每个非空栅格内的点数ni,得到每个非空栅格的点云出现频率pi为:
(1)
点云P在该平面的投影熵SE定义为:
(2)
1.2 投影
在工程制图中,通常采用三视图来表达物体的形状和各部件的相对位置关系。因此,三视图能完整地表达各部件的相对位置关系。一个物体确定后,其各个部件的相对位置关系也就确定。点云配准本质为找出点云之间的相对位置关系。因此,通过确定空间点云的投影位置,就能确定空间点云的位置关系。空间点云三坐标平面投影如图1所示。

图1 空间点云三坐标平面投影图
由图1可知:两个错位(未配准的)点云模型在二维平面的投影是不重合的,两重合(配准后的)点云在二维平面的投影是重合的。本文基于此原理,提出了一种降维评价三维空间点云位置关系的新方法。
1.3 信息熵评价点云空间位置关系
对于待配准的两片点云,由图1可以看出,当两片点云的角度没有偏差的时候,其投影也没有偏差。当点云角度偏差为0°时,两片点云在该平面上的投影相对聚集。此时,投影点云分布密度的不均匀性最大。当点云角度偏差不为0°时,由于两片点云不在同一坐标系下,故投影点云将较为均匀分布在整个投影平面上。此时,投影点云分布密度的不均匀性较小。由不同点云偏差角度可得到不同的投影点云分布,因而有望利用投影点云分布密度估计点云的空间位置。
根据空间点云仅在一个平面的投影,不能非常精确地估计点云位置关系。如在点云位置相差90°时,利用一个平面的投影尚不能估计出点云空间位置关系。而利用三个坐标平面投影熵之和,能消除点云错位90°不能估计的情况。
将两片点云投影到XY、YZ、XZ三坐标平面,依据式(1)和式(2)计算得到点云在XY、YZ、XZ平面的投影熵,分别为SEXY、SEYZ、SEXZ。
定义总的点云投影熵E为:
E=SEXY+SEYZ+SEXZ
(3)
从式(3)可知,点云的投影分布越密集,总投影熵就越小。
2 基于投影的点云配准
本文采用总投影熵作为遗传算法的目标函数,来寻找空间变换的最优解。第一步是设置空间最大的变换空间;第二步是初始化目标种群并计算其适应度值;第三步是进行个体选择、交叉和变异以产生子代个体,直到满足设定的遗传代数或目标函数收敛的条件来终止遗传算法;第四步是得到最优空间变换矩阵,并应用于配准点云,得到配准结果。
2.1 变换空间
两次扫描的点云空间坐标系是任意的,而在遗传算法中需要设置其变换空间最大范围。因此,需要寻找出最大变换空间。算法的求解步骤如下。
①设点云P中有N个点,点云Q中有M个点,分别计算出中心。计算式为:
(3)
(4)
②中心化点云。
(5)
③计算出两片点云在X、Y、Z方向上的最大值和最小值。
④旋转矩阵R参数。
对于旋转矩阵[α,β,γ],如果确定了绕轴旋转的角度α、β、γ,就能求解旋转矩阵。在三维空间中,绕其中一个坐标轴最大转动角度为2π,因此选用旋转角度取值区间为[-π,π],则α∈[-π,π]、β∈[-π,π]、γ∈[-π,π]。
⑤平移矩阵T参数为:
(6)
(7)
(8)
2.2 编码方案
本文使用给定长度的二进制符号串来表示群体中的个体,其等位基因由二值符号集{0,1}所组成。
①编码。设某一参数的取值范围为[W1,W2],采用长度为u的二进制编码符号来表示该参数,则它共能产生2u种不同的编码,可使参数编码时的对应关系为:
0000L 00=0→W1
0000L 01=1→W1+σ
0000L 02=2→W1+ 2σ
… …
1111L 11=2u-1→W2
式中:W1为参数取值下限;W2为参数取值上限;u为编码长度;σ为编码间距。
②解码。假如某一个体的编码为bubu-1…b2b1,则对应的解码公式为:
(9)
2.3 适应度函数
在遗传算法中,个体的适应度大小决定了该个体被淘汰的概率。个体的适应度值越小,其越可能被淘汰。而在本文中,需要目标函数值越小越好,适应度值越大越好。所以,通过目标函数构造的适应度函数为:
FitnV=CE
(10)
式中:E为总投影熵;C=0.618。
2.4 算法实现
本文遗传算法的各进化算子分别采用轮盘赌方法、单点交叉和单点变异,并将空间三坐标平面的投影熵之和作为遗传算法的目标函数。算法步骤如下。
①最大变量域中初始化种群P,并设定最大遗传代数G。
②种群P分别作用于目标点云,求取每次初始变换空间的X、Y、Z坐标方向最大最小值,确定最大变换空间位置。
③计算个体的目标函数和适应度值。
④选取种群中最优个体,得到其总的点云投影熵E,令全局最小总的点云投影熵Emin=E。
⑤根据适应度值进行优良个体选择并使用最优保存策略,对选择的种群进行交叉和变异操作,产生新一代进化种群。
⑥求解新一代种群所有个体的适应度值FitnV,比较该代最优个体的总的点云投影熵SE′和全局最小总的点云投影熵Emin。如果E′ ⑦检查当前代数是否达到最大代数G,以及E是否收敛。若没有达到,则转到步骤⑤,继续求解;否则,输出全局最优个体,解码得到空间最优旋转、平移矩阵。 ⑧更新点云位置,输出配准点云。 基于投影的点云配准算法流程如图2所示。 图2 基于投影的点云配准算法流程图 为了验证算法的可行性、鲁棒性和有效性,在Intel Core-i5、8 GB内存的Windows 7操作系统中,基于MATLAB平台进行配准试验。该试验主要以有缺陷和有大量噪声点的点云来进行验证。 图3 不同算法的空间位置评价示意图 由图3可知:MSE、SDE和总投影熵算法都能满足空间位置的评价。当点云完全配准时,三种评价算法都是全局最小。但此过程中,MSE算法运行时间为93.159 s,SDE算法运行时间为3.135 s,本文算法(总投影熵)运行时间为2.527 s。由此说明,本文算法耗时最少。由于遗传算法寻优时需要不断评价个体的空间位置,因此需要频繁的调用。而本文算法在满足准确性要求的条件下,具有快速性的特性,很适合作为遗传算法目标函数。 为了说明本文算法的有效性,将本文算法分别应用于完整的、部分缺失的、有噪声的点云模型。不同类型模型的配准效果如图4所示。由图4可知:本文的粗配准算法对于三种点云模型都具有很好的配准效果,能够为精配准算法提供优良的初始位置。设定最大遗传代数G=80,初始种群的个体数为80,交叉概率为0.9,变异概率为0.09。 图4 不同类型模型的配准效果图 以图4中(a)模型为例,图5为遗传代数与适应度值的变化关系图。 图5 遗传代数与适应度值变化关系图 图5显示了每一代种群适应度平均值和每一代种群中最优个体的适应度值。本文的配准算法采用遗传算法作为搜索策略。由图5可知:随着遗传代数的增加,种群朝着最优解的方向遗传进化,最优个体也随着遗传进化而趋近于全局最优解。由此说明,本文采用遗传算法求解最优空间变换矩阵是有效的。 为了验证本文算法的优异性,选用四种粗配准算法进行比较。不同算法的配准效果对比如图6所示。图6(b)为文献[2]中的PCA算法;图6(c)为文献[12]中四点匹配法(4-point congrugent set,4PCS);图6(d)为文献[6]中MSE算法;图6(e)为文献[5]中SDE算法。以下模型是西南科技大学奖杯,参考点云是完整的点云,目标点云是含有部分噪声的点云。设定最大遗传代数G=50,初始种群的个体数为40,交叉概率为0.9,变异概率为0.05。由图6可知:PCA算法配准效果最差,4PCS和MSE算法配准效果较好,SDE算法配准效果不够理想,本文算法效果最好。 图6 不同算法的配准效果对比图 不同算法运行时间对比如表1所示。 表1 不同算法运行时间对比 Tab.1 Comparison of running timeof different algorithmss 模型算法PCA4PCSMSESDE本文奖杯1.21100.65110.6370.6560.32 由表1可知:PCA算法用时最少,本文算法相对4PCS、MSE和SDE算法用时较少。再结合图6结果,可得本文算法的配准性能最高。 本文通过计算三视图中的投影熵来描述两片点云的位置关系,提出了一种降维评价点云空间位置的方法。由于可以把点云配准作为优化问题处理,利用该评价方法简单快速的特点,再采用遗传算法作为搜索方法、投影熵作为目标函数,可以准确、快速地寻找出最优的匹配。该配准算法利用了遗传算法,但还没有充分挖掘遗传算法的特性,在运行效率方面可以进一步提高。
3 试验结果与分析
3.1 点云空间位置关系


3.2 不同类型模型配准结果分析
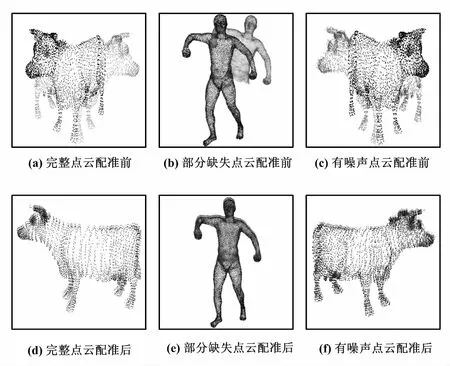
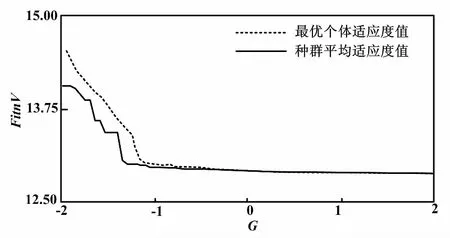
3.3 不同粗配准算法效果比较


4 结束语

