考虑顾客感知价值的零售商动态定价模型

王清漪，徐 菱

（西南交通大学，四川 成都 611756）

1 引言

季节性产品如时尚品、电子产品不同于一般商品，通常生产周期长、销售周期短，新产品往往只有一次订货机会。除此之外，季节性产品还具有这一显著的特点：随着产品上市时间的推移，顾客感知价值（Customer Perceived Value,CPV）逐渐降低，这种现象很大程度上影响消费者的购买决策，从而导致了产品市场需求的不确定性[1]。消费者的这种心理预期损失主要是由两方面原因导致的，一方面是由于产品本身的价值降低导致的，比如生鲜农产品，其新鲜度随着上架时间的推移而受损；另一方面是由于消费者本身购买意向降低导致的，比如对于电子产品，新款电子产品对消费者更具有吸引力，早到的顾客往往比晚到的顾客具有较高的预期价格以及较低的价格敏感度[2-3]。然而，在不完全竞争下，大多数时尚零售商可能表现出一些垄断行为，并通过定价影响需求结构[4]。

对于季节性产品，跨期定价机制具有较高的应用价值。从管理角度来说，跨期定价有利于市场细分，同时离散的定价较易于实施；另一方面，为达到期望利润最大化的目的，零售商可以根据库存及需求的波动调整价格。因此，在顾客感知价值衰减的情况下，零售商为了管控库存和扩大市场，必须根据市场需求状况动态的调整产品的零售价格。

跨期定价是零售商针对具有不同偏好的潜在顾客使其自身利润最大化的常用做法，这种策略在改善零售商收益方面被证明比单一的定价策略更为有效[5]。目前学者对动态定价及订货批量决策问题进行了大量研究，Zhou等[6]研究了新款时装的两阶段最优定价策略，并得出最优策略取决于生产成本和顾客保留价格。吴胜等[7]将产品销售周期分为时尚期和衰退期，建立了基于消费者时间偏好和价格依赖的多阶段动态定价模型。P-S[8]探讨了折扣率固定时易逝品订货批量及最优动态定价问题。Akcay等[9]在消费者选择行为下，研究了零售商在给定初始库存量和销售时间下的易逝品最优动态定价问题，并讨论了产品横向和纵向差异情形下，产品的最优价格策略与质量、库存和时间的单调性关系。

上述研究内容在对产品的市场需求建模时主要考虑价格和时间因素，而感知价值作为顾客评价季节性产品的重要指标，是影响季节性产品市场需求的另一重要因素。颜莉等[10]认为时尚产品的定价应以感知价值为基础，并且对顾客感知价值相关因素进行量化，在此基础上构建了时尚产品的一般定价模型和拓展定价模型。周建亨等[11]假设顾客感知价值具有相同的时间偏好，研究了供应链订货策略。刘思婧等[12]考虑快速时尚品的价格衰减与顾客需求量的关系以及配送时间等因素，建立在网络销售环境下的物流网络规划模型，并分析了退货率对网络收益的影响。生鲜产品背景下，顾客感知新鲜度实质上即感知价值，陈奕娟等[13]讨论了生鲜产品新鲜度随时间衰退背景下，超市的最优动态定价策略。唐磊等[14]研究了顾客感知价值服从指数分布时，生鲜零售商的最优订货量及动态定价策略。王道平等[15]考虑需求受新鲜度和价格影响下，引入收益共享和价格补贴的联合契约，对生鲜农产品订货量和两阶段价格的降价时点进行了有效的决策。

以上研究对象均为生鲜农产品或时尚产品中的时装，而针对季节性流行产品多阶段动态定价缺乏研究和探讨。基于此，本文研究了顾客感知价值衰减及价格影响下的动态定价问题。首先将产品销售周期划分成若干阶段，每个阶段对应不同的零售价格，采用指数函数刻画顾客感知价值的衰减规律，同时考虑价格弹性因子波动，给出各阶段的实际市场需求，然后，以总期望利润最大化为目标建立动态定价模型，并运用动态规划的方法求出各阶段最优零售价格，最后，完成定价次数、衰退因子及价格弹性因子对零售商利润及最优零售价格的灵敏度分析。

2 问题描述与假设

季节性流行产品具有产品生命周期短、产品需求变化大的特点，产品上市之后将会经历短暂的流行期，随着新的流行元素出现或者季节变化，顾客感知价值不断下降，顾客需求会受到理性行为的影响。因此，本文将结合产品生命周期特征及消费者有限理性行为理论，探讨时尚产品的动态定价问题。本文建立模型将用到的假设和符号说明如下：

（1）外部需求x为连续型随机变量，概率密度函数为f(x)，累计概率分布函数为F(x)。

（2）将销售期划分为N个阶段，因此零售商在产品销售的第i阶段制定的价格为pi。零售商需在销售期开始前即t=0时给出产品定价策略P={p1,p2,…,pN}，该策略一旦制定，在整个销售期内无法改变。

（3）由于产品供应前置期长，销售周期短，故零售商只能订购一次，订购批量为q，采购单价为c。假设采购及价格变动成本为沉没成本，销售周期结束时的剩余库存会被供应商全部回购，回购单价为ω。

时尚品、电子产品等季节性产品随着产品发布时间的推移，其在消费者心目中的价值（由时尚和功能两个方面构成）逐渐衰减[16]。Andersen等[17]指出,反映消费者理性行为随时间变化的指数贴现函数比双曲贴现函数更稳健，因此本文利用指数函数β(t)=γθt来刻画顾客感知价值的衰减规律，式中θ为功能型因子，γ为时尚型因子，0＜θ＜1，0＜γ＜1，t∈[(i-1)T,iT]，其中i=1,2,…,N。该函数具有以下性质：（1）是关于时间t的连续单调减函数，并且近期下降速度较为迅速，远期下降速度较为平缓。（2）β(t)取值范围为[0,1]，β(0)=1时，表示产品在初始时刻处于最流行的状态。

本文结合需求函数的特性，采用文献[18]中的乘积形式，定义顾客需求函数形式为：

其中：p为零售价格（p＞1），价格弹性系数η是指市场商品需求量对于价格变动做出反应的敏感程度，也就是说，价格弹性越大，顾客需求对价格变动越敏感，且η在销售期间逐渐增大（η＞1）。这一假设有助于市场细分，因为多级定价的背景下存在战略性和折扣搜索型的顾客，这类顾客对于价格变动的敏感性高。

3 市场需求函数分析

基于上述假设可知，整个销售期被划分为N个阶段，考虑顾客感知价值衰减及价格因素时，产品在其第i（i=1,2,…,N）个销售阶段的市场需求为：

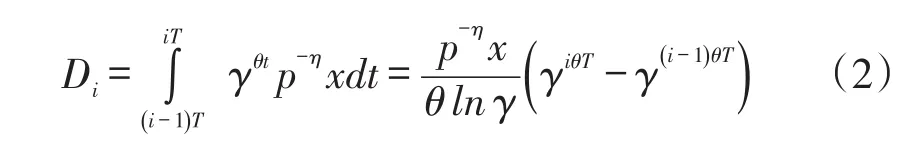
进一步得到销售期第i阶段实际市场需求Di与外部需求x的关系：

其中，φi为第i阶段影响外部需求的总需求系数,

定理1 产品在销售期第i阶段（i=1,2,…,N）时，总需求系数φi与功能型因子θ呈负相关，与时尚型因子γ呈正相关，并且随着价格弹性系数η的增大而减小。

证明：已知其 中i=1,2,…,N，可得到：

令t1=iT，t2=(i-1)T，构造函数可知ρ(t)是关于t的单调增函数，又因为t1＞t2，0＜θ＜1，0＜γ＜1，因此≤0，φi关于功能型因子θ呈负相关。

同理可得：

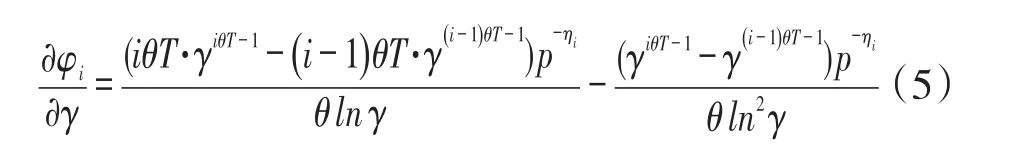
由定理1和式（3）可知，外部需求x确定后，实际市场需求Di是时尚型因子的单调增函数，是功能型因子及价格弹性因子的单调减函数。因此，在商业运作中，零售商应根据实际市场需求的波动制定动态价格策略，从而增加收益。接下来考虑顾客感知价值衰减和价格敏感度对零售商利润的影响，并建立模型求解零售商最优定价策略。

4 考虑顾客感知价值衰减的零售商动态定价模型

4.1 零售商动态定价模型

由于不考虑需求波动性，外部需求x是连续的随机变量，概率密度函数为f(x)，累计概率分布函数为F(x)。考虑价格和时间因素影响下的需求量时，假设第i阶段需求数量Di的概率密度函数为φ(Di)，累计概率分布函数为Φ(Di)，其中i=1,2,…,N。由上述分析可知，实际市场需求Di和外部需求x的概率密度函数关系为：

由式（2）销售期各阶段实际市场需求量可得，销售期第i阶段的期望销售量为：

由式（7）可知，初始订货量为q=q1，销售期第i阶段（1＜i≤N）的初始库存量为：

因此，销售期第i阶段结束时的期望库存剩余量为：

销售期第i阶段利润函数为：

引理1 对任意销售阶段i（i=1,2,…,N），该阶段零售价格pi不能令初始库存qi小于该阶段的需求Di，即零售价格pi的制定应满足qi＞Di或qi=Di[18]。

说明：假设决策者制定价格策略时，预测到销售期的某个阶段qj＜Dj（1＜j≤N），这种情形下，决策者只需保持阶段1到阶段j-1的价格不变，单独提高第j阶段价格直到qN=DN，即可增加利润。

由引理1，对式（10）进行加总化简后得到零售商在整个销售期内的总期望利润Ω(P)

其中：pN+1=ω。

4.2 模型求解

由式（11）可知，零售商最优定价问题是一个动态决策问题。考虑将销售周期分为N阶段，以零售商总期望利润最大化为目标，最优定价策略P=是决策变量，建立如下动态规划模型：

约束条件为：

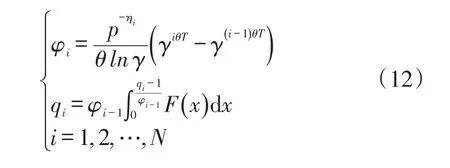
为了分析零售商在各销售阶段的最优价格（i=1,2,…,N），将动态规划模型目标函数分为以下N阶段进行求解：

第i阶段（1≤i＜N）的期望利润为：

第N阶段（清货期）的期望利润为：

以各阶段利润最大化为目标，即可求解出最优零售价格。为方便分析，我们讨论外部需求x服从均匀分布的情况，并假设x～U( 0,b)。

定理2：在任意销售阶段i（1≤i＜N），若则最优零售价格可由=0求解得出，否则

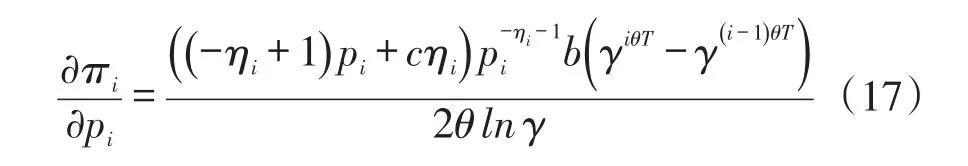
定理3：在销售期第N阶段（清货期），若最优零售价格可由式=0得出，否则

证明：定理3和定理2的证明过程类似，不再赘述。

定理2、定理3给出了市场需求服从均匀分布的情况下，阶段最优零售价格存在，从最优零售价格形式来看，得出以下结论：（1）各阶段最优定价策略的制定过程中，阶段时长、价格敏感度和订货量都是影响定价的重要原因。（2）清货期最优定价与采购成本无关，与回购价格有关，显然，零售商为了规避风险通常会在清货期选择低于成本的零售价格。

5 算例分析

某零售商计划上新一款时尚品，假设相应的参数为：NT=8，c=80，ω=15，b=4 500，q=10，ηi∈[1.2,1.6]，价格弹性系数ηi在销售期不同阶段有所增加。

首先分析定价次数对零售商利润及定价策略的影响，假设时尚型因子γ=0.6，功能型因子θ=0.5，当定价次数N={1,2,3,4,5}时，零售商在N销售阶段的最优定价策略及最优收益见表1。

表1 不同定价次数时最优定价策略及零售商收益

从表1可以看出：在一定的范围内，定价次数增加，零售商期望利润增加，期末剩余库存数量减少。随着时间推移，各阶段最优价格逐渐降低，清仓期可能会出现最优零售价格低于成本的情况，这是因为回购价格低，零售商为了止损只能低价出售。

然后，探讨顾客感知价值的相关参数对零售商利润及定价策略的影响。假设时尚型因子γ=0.7，当功能型因子θ={0.5,0.6,0.7,0.8}时，零售商在各个销售阶段的最优定价策略及最优收益见表2。

表2 不同功能型因子θ下的最优定价策略及零售商利润

从表2可知，随着θ减小，期末剩余库存数量减少，总体最优定价水平上升，零售商期望利润增加。这是由于功能型因子θ减小，意味着产品具有更高的实用价值，销售期各阶段顾客感知价值及需求均有所增加，因此零售商利润上升。

进一步，分析不同时尚型因子γ下的最优定价策略及零售商利润的影响。假设N=5，θ=0.3，当时尚型因子γ={0.35,0.45,0.55,0.65}时，零售商在各个销售阶段的最优定价策略及最优收益见表3。

表3 不同时尚型因子γ下的最优定价策略及零售商利润

由表3可知，销售期各阶段的最优价格及零售商利润随着时尚型因子的增大而增加。这是由于γ越大，销售期各阶段顾客感知价值及需求均增加，剩余库存减少，因此零售商利润上升。对比表2和表3可知，销售期各阶段的最优价格及零售商利润受时尚型因子影响较大，受功能型因子较小，也就是说顾客感知价值对时尚因素较为敏感，这与产品特点有关。

最后，分析价格弹性对零售商利润及定价策略的影响。假设N=5，时尚型因子γ=0.6，功能型因子θ=0.5，当弹性系数η不同时，零售商在各个销售阶段的最优定价策略及最优收益见表4。

表4 不同弹性系数η下的最优定价策略及零售商利润

由表4可知，顾客感知价值的敏感性越低，产品在各个销售阶段的价格越高，期末剩余库存越小，最终零售商利润上升。易知η越小，顾客对产品的感知价值就越高，销售期各阶段需求和价格随之增加，因此零售商利润上升。

6 结语

本文研究了顾客感知价值衰减及价格弹性因素影响下的时尚产品的动态定价问题，采用指数函数描述顾客感知价值的衰减规律，设计了时尚型因子及功能型因子以实现销售期内顾客感知价值的准确定位。以零售商利润最大化为目的建立动态定价模型，并使用动态规划算法求解其最优定价序列，最后，利用具体算例验证了模型的可行性。主要研究结论为：（1）随着定价次数的增加，动态定价策略能够加速商品流通，从而增加零售商的期望收益；（2）产品的时尚型因子与零售商最优收益及各阶段最优零售价格正相关，而功能型因子和价格弹性因子则相反。

考虑到本文的模型构建和分析是基于特定的假设条件，可以从如下两个方面做进一步的研究：（1）本文简单假设了价格弹性系数在销售期不同阶段线性增加，并未进行深入的研究，实际上多级定价的背景下存在战略型和折扣搜索型的顾客，这类顾客对价格变动的敏感性高，尤其是折扣搜索型顾客，因此进一步的研究可以考虑市场上存在不同类型顾客的情形。（2）本文假定外部需求服从均匀分布，顾客感知价值的衰减为指数函数的形式，得出的结论只在一定条件下成立，进一步的研究可以考虑外部需求服从指数分布、正态分布的情形等。