海南省无性系木麻黄可变参数二元立木材积模型研建

黄四南

(湖南省临湘市林业局， 湖南 临湘 414300)

林业数表是我国各类森林资源调查和森林经营决策必不可少的计量依据，是森林资源与生态状况调查、监测和评价的“度量衡”，是森林资源经营管理的基础计量工具[1]。木麻黄(Casuarinaequisetifolia)为木麻黄科木麻黄属常绿乔木，由于良好的抗风性和耐干旱、耐贫瘠性，木麻黄在中国东南沿海地区被广泛地应用于防护林建设中。自20 世纪50 年代起，海南省在环岛区域引种木麻黄，并开展优良无性系选育和造林等相关研究[2]。海南省木麻黄主要以无性系人工林为主，从第九次清查结果来看，海南省木麻黄面积1.2万hm2，蓄积量为53.69万m3[3],是海南省主要人工林树种之一。但由于受多方面因素影响，海南省木麻黄一直未编制材积表模型。为满足林业生产经营管理需要，依据海南省无性系木麻黄实测样本数据，建立通用的二元立木材积模型。同时，客观分析干形随胸径(D)和树高(H) 的变化规律，构建可变参数二元立木材积模型，以期寻求符合客观规律，以及精度更高、切合性能更强的二元立木材积模型，为完善海南省森林资源监测体系提供重要计量依据。

1 数据

为保证木麻黄立木材积模型的通用性，在样本组织方面，须尽可能扩大样本变量的覆盖范围，真实反映变量间相互存在的客观规律。样本采集时，将木麻黄的取样范围按胸径分为6，10，14，18，22 cm和26 cm以上共6个取样点位，在每个点位上取样时要求尽量按树高的实际变化范围分低、中、高(以高径比控制)选取样木，伐倒后进行区分实测。本次研建共采集了150株建模样本和66株检验样本(表1)，采集区域主要分布在琼海市、文昌市和万宁市。

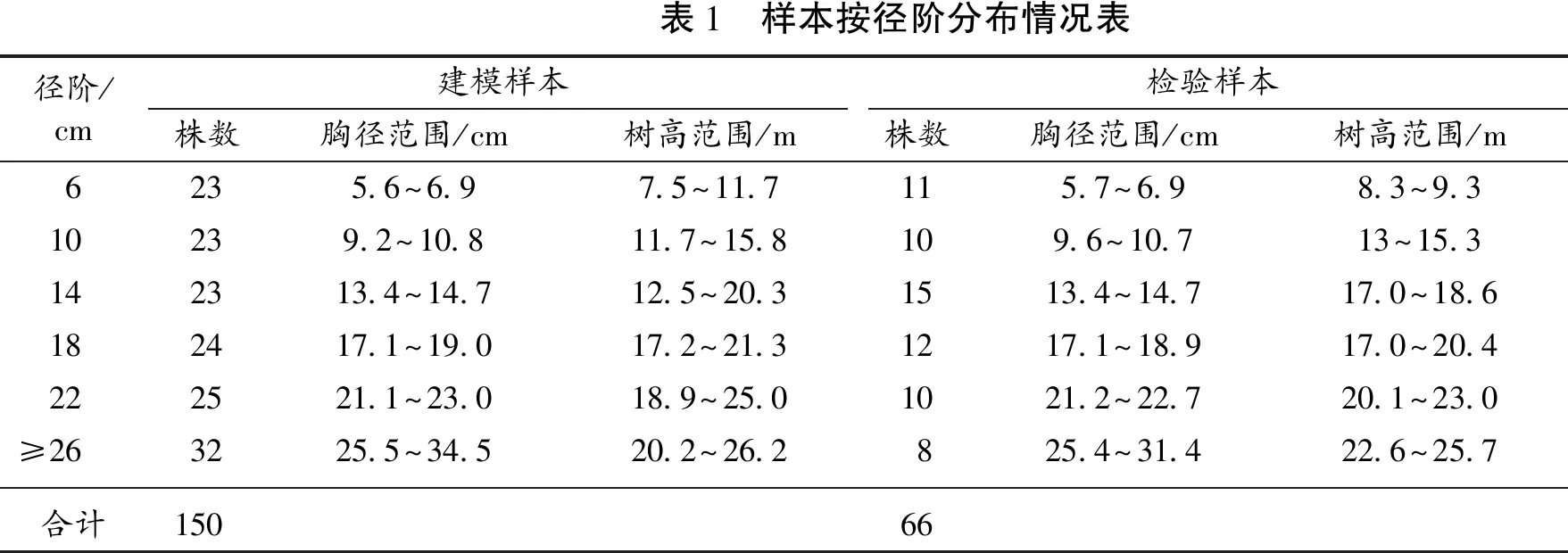
表1 样本按径阶分布情况表径阶/cm建模样本检验样本株数胸径范围/cm树高范围/m株数胸径范围/cm树高范围/m6235.6～6.97.5～11.7115.7～6.98.3～9.310239.2～10.811.7～15.8109.6～10.713～15.3142313.4～14.712.5～20.31513.4～14.717.0～18.6182417.1～19.017.2～21.31217.1～18.917.0～20.4222521.1～23.018.9～25.01021.2～22.720.1～23.0≥263225.5～34.520.2～26.2825.4～31.422.6～25.7合计15066

2 研究方法

2.1 模型构建

1)固定参数模型。经相关研究表明[4-5]对于主干材积而言，山本材积式能较好地反映干形随胸径(D)和树高(H)变化的规律，模型的结构式为：

V=C0×DC1×HC2

式中：V为材积(m3)，D为胸径(cm)，H为树高(m)，Ci为模型参数。

2)可变参数模型。为充分利用了样本资料所反映的信息，使其参数能追踪形数的变化，从而更加客观反映材积随胸径和树高变化的客观规律，提高模型预估精度。本文中的动态模型主要以山本材积式为框架，将样本按照不同径阶和树高级进行划分，通过固定山本材积式进行拟合，分析固定参数模型中C1和C2随径阶和树高级的变化规律，将可变参数模型结构式设计为：

V=C0×DC1-C2×(D+H)×HC3+C4×(D+H)

式中：V为材积(m3)，D为胸径(cm)，H为树高(m)，Ci为模型参数。

2.2 异方差性的消除

由于立木材积等数据普遍存在着异方差性，在求解模型参数时必须采取措施消除异方差的影响。本次建模将采用加权回归方法，每个方程的权函数采用模型本身[6]。

2.3 模型评价

通常模型检验评价的统计指标采用以下几项：相关系数(R2)、估计值的标准误差(SEE)、平均预估误差(MPE)、平均预估精度(P)、平均百分标准误差(MPSE)、总相对偏差(TRB)和平均系统偏差(MSB)。具体计算公式参见文献[7]。

另外，参数的稳定性是判定模型是否可用的重要指标，一般以参数变动系数不超过±50 %为识别标准。计算公式如下：

为检验模型的全面切合性能，本文中对模型采用分径阶检验，主要以总相对偏差(TRB)和平均系统偏差(MSB)两个指标衡量在各径阶下是否存在明显系统偏差(TRB和MSB在±5以内)；同时利用模型残差与模型自变量作残差分布图，对残差分布的随机性进行判断，模型全面切合性能高，残差应为随机分布(各阶径的残差正负相抵，以0为基准线上下对称分布)。

3 结果分析

3.1 模型拟合结果

模型拟合时，考虑到消除异方差对模型质量的影响，以模型本身为权，均采用加权最小二乘法进行拟合。具体固定参数模型和可变参数模型的参数估计值及相关评价指标见表2。

从拟合结果来看，无论是固定参数模型，还是可变参数模型拟合效果均很好。模型的R2均达到了0.99以上，表明模型拟合效果较好；无论固定参数模型还是可变参数模型平均预估精度较高，均到达了98%以上，但两者平均预估精度差异很小，且两者MPSE均在±5%以内。固定参数模型中参数估计值的变动系数均小于20%；可变参数模型中C2和C4两个参数估计值的变动系数超过50%以上，主要原因在于干形随胸径和树高的变化趋势不明显，从固定参数模型和可变参数模型的评价指标可知，可变参数模型整体评价指标并没有显著提高。

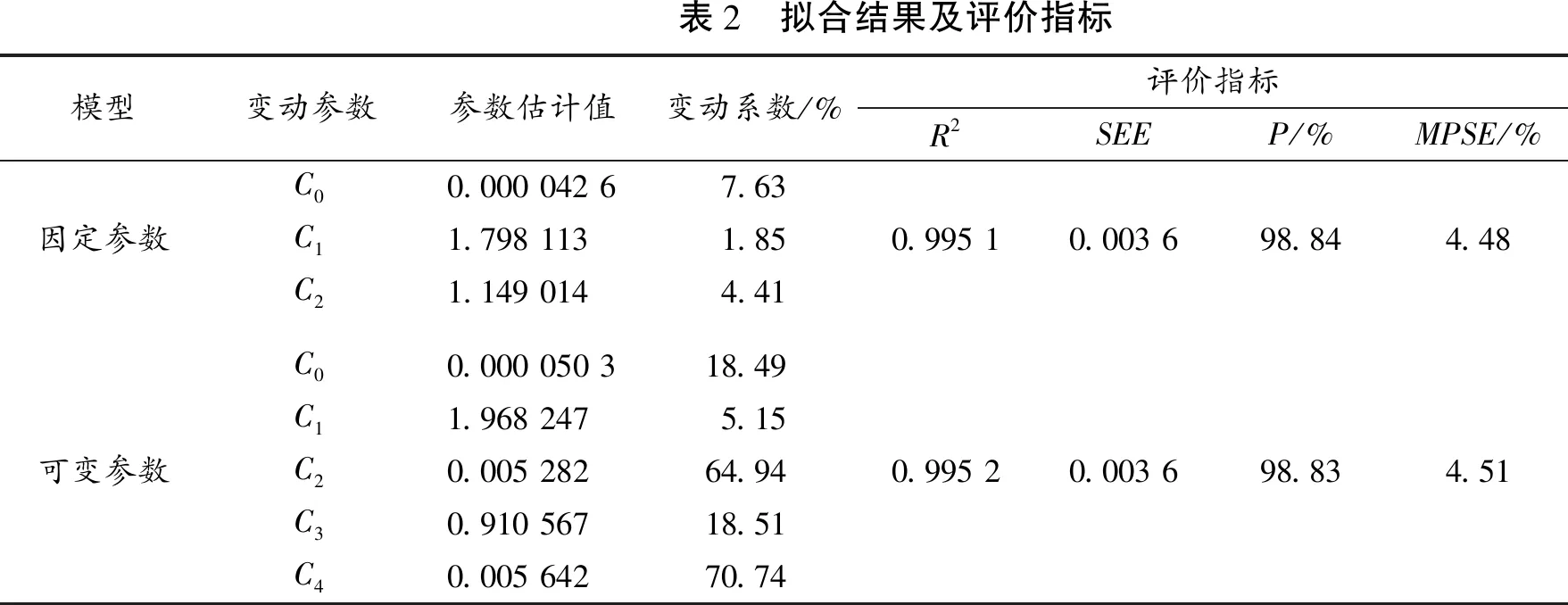
表2 拟合结果及评价指标模型变动参数参数估计值变动系数/%评价指标R2SEEP/%MPSE/%C00.000 042 67.63因定参数C11.798 1131.850.995 10.003 698.844.48C21.149 0144.41C00.000 050 318.49C11.968 2475.15可变参数C20.005 28264.940.995 20.003 698.834.51C30.910 56718.51C40.005 64270.74

3.2 分径阶检验结果

利用检验样本对固定参数模型和可变参数模型进行分径阶检验(表3)，固定参数模型和可变参数模型在整体上TRB和MSB指标均在±1%以内，这表明从整体上看，两种模型都不存在明显系统偏差。但是，对各径阶进行分析，可变参数模型在各径阶上TRB和MSB指标均优于固定参数模型，尤其对于大径阶和小径阶效果更加明显。因此经分径阶检验，可变参数模型的全面切合性能要优于固定参数模型。

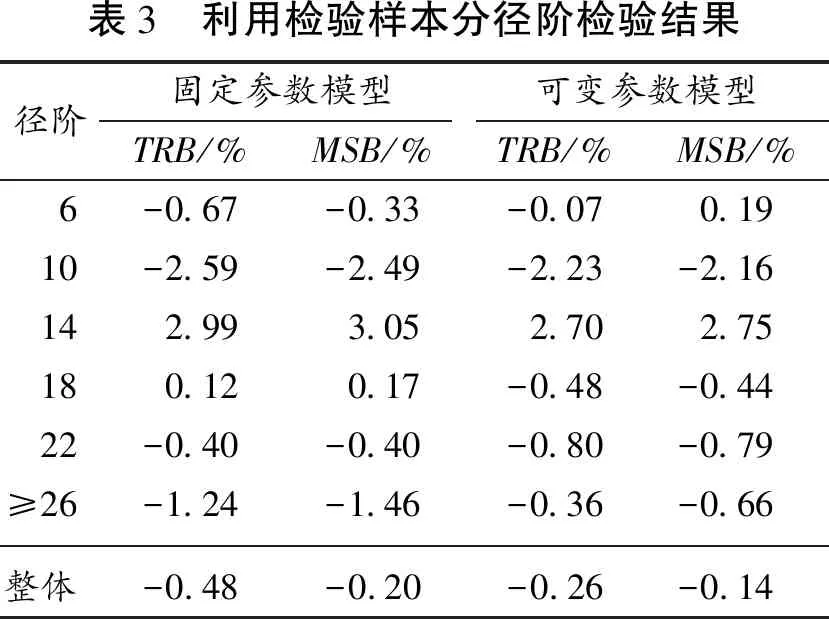
表3 利用检验样本分径阶检验结果径阶固定参数模型可变参数模型TRB/%MSB/%TRB/%MSB/%6-0.67-0.33-0.070.1910-2.59-2.49-2.23-2.16142.993.052.702.75180.120.17-0.48-0.4422-0.40-0.40-0.80-0.79≥26-1.24-1.46-0.36-0.66整体-0.48-0.20-0.26-0.14

3.3 残差分布

从图1，图2可以看出，在整个径阶分布范围内，固定参数模型和可变参数模型的残差基本上服从随机分布，残差分布范围在±0.1以内。但是，相对于固定参数模型残差分布，可变参数模型残差在中轴线附近分布更加紧凑；尤其在大径阶范围内，可变参数模型残差分布范围明显小于固定参数模型残差分布范围，因此可变参数模型在大径阶范围内预估精度更高。这也更加直观的表明了，可变参数模型的全面切合性能要优于固定参数模型。

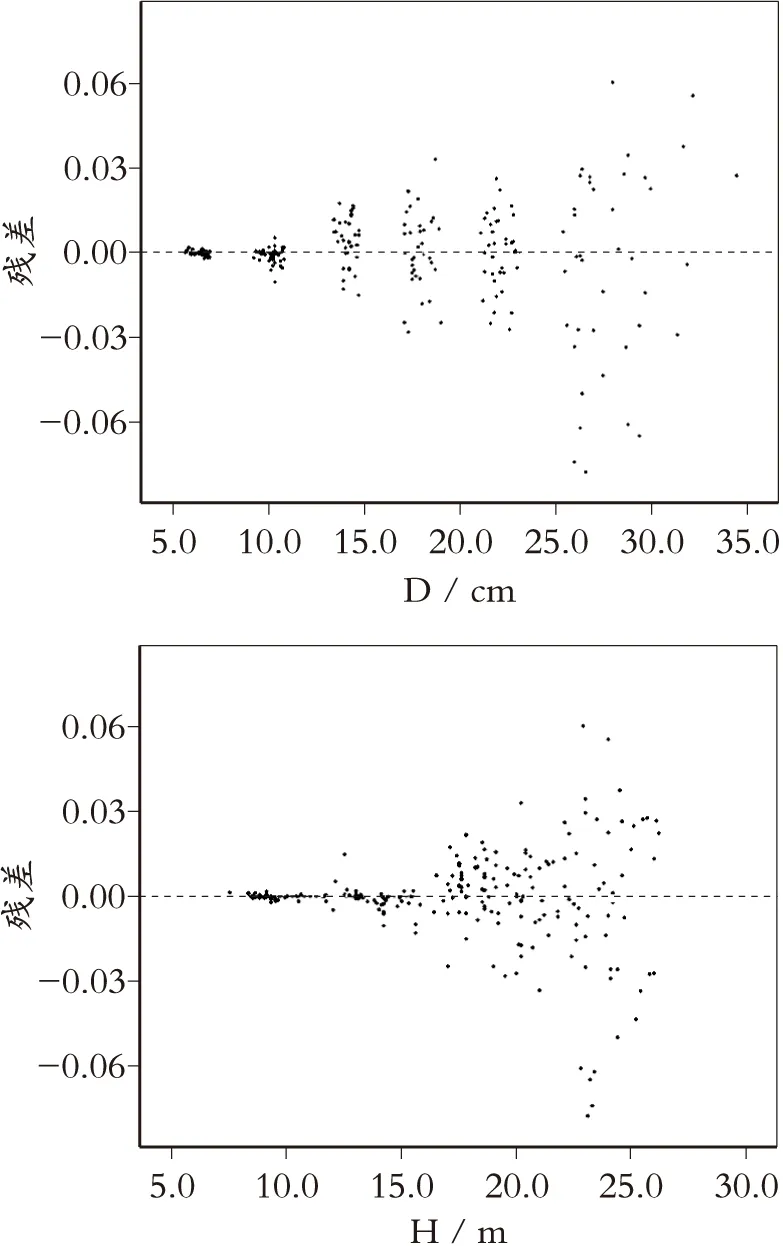
图1 固定参数残差随胸径与树高分布图

图2 可变参数残差随胸径与树高分布图

4 结论

本文分别采用固定参数的山本材积式模型为基本模型结构，通过分析干形随胸径(D)和树高(H)的变化趋势，构建可变参数动态材积模型结构，建立了海南省无性系木麻黄二元立木材积模型。经通用模型评价指标分析、分径阶检验和残差随机性检验可以得出以下结论：

1)海南省无性系固定参数二元立木材积模型和可变参数二元立木材积模型的预估精度较高，均超过了98%；整体上，两种模型的TRB和MSB指标均在±1%以内，完全满足林业数表建模要求。

2)尽管可变参数模型的整体评价指标相对于固定参数模型没有显著提高，但是通过分径阶检验和残差随机性检验，检验模型在某一局部径阶范围内切合性能，可变参数材积模型全面切合性能要明显优于固定参山本材积式模型。