基于模糊聚类的混合多传感器数据融合算法

朱明荣，盛子恒

(1.中国船舶重工集团公司第七二三研究所，江苏 扬州 225101；2.新南威尔士大学，悉尼 2052)

0 引 言

数据融合又称为多传感器数据融合[1]，即将多传感器获得的数据进行分析、处理，通过运用一定的计算机技术充分挖掘出数据所蕴含的全部信息，进而对其作出相应的估计和决策，以减少由单传感器产生的不确定性。多传感器数据融合是对人类认知现实世界的一种模拟，广泛应用于军事领域中的目标识别、敌我态势评估与决策等问题。聚类分析是一种经典的数据融合算法，其中模糊C均值聚类(FCM)算法具有运行时间少、自动对样本数据进行分类等[1]优点，其在医学图像分割、生物种群认知、网站信息检索、用户商业选址等[2]领域应用广泛。但随着物联网的发展、环境的多样性、多传感器种类以及数据的多样性，利用传统的模糊聚类方法已不能对它们进行恰当的分类。文献[3]提出了一种EFCM(Fuzzy C-means Based on Effective Distance)算法，该算法充分考虑了数据的分布结构，通过采用稀疏重构的方法来度量数据之间的距离，即有效距离；文献[4]提出了一种FDP-FCM(Find Density Peaks Fuzzy C-means Clustering)算法，该算法通过引入加权系数并采用高斯核函数找到局部密度最大的点，并将其作为初始聚类中心，解决了传统的基于聚类的数据融合算法对初始聚类中心敏感、无法确定聚类数目、收敛速度慢等问题；文献[5]提出了一种IIFCM(Improved Intuitionistic Fuzzy C-means)算法，该算法通过在损失函数中引入了直觉模糊因子，并结合局部空间信息来克服噪声与空间的不确定性问题；文献[6]提出了一种AFCM(Adaptive Fuzzy C-means)算法，该算法通过引入自适应系数不断优化损失函数，能很好地处理噪声与不同密度的数据集，但不能处理具有混合属性的数据集且随机初始化的聚类中心易使其陷入局部最优；文献[7]提出了一种CH-CCFDAC(a New Clustering Center to Quickly Determine the Clustering Algorithm)算法，该算法通过结合CCFD(Cluster Center Fast Determine Algorithm)与改进的迭代爬山算法(Improved Mountain Climbing Algorithm)确定了聚类中心，但受截断距离的影响，其不能处理具有噪声与不同密度的数据集。

为此，本文对文献[7]进行改进，提出了一种基于模糊聚类的混合多传感器数据融合算法，简记为HFCM算法。该算法首先在CH-CCFDAC算法中采用高斯核函数进行局部密度度量以确定初始聚类中心，其次结合AFCM算法的聚类结果设计了一种融合策略。通过在UCI数据集上的仿真实验，结果表明本文算法不仅能够处理具有噪声与不同密度的混合属性数据集，还有效地提高了融合效果，较好地解决了舰船异质传感器及其不同数据属性的数据融合问题。

1 HFCM算法

1.1 HFCM算法思想

在CH-CCFDAC算法中，局部密度度量采用的是分段函数，其具体形式如下：

ρi=∑f(dij-dc)

(1)

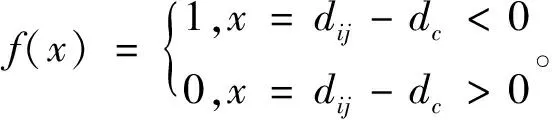
从距离ρ=(ρ1,ρ2,…,ρn)的定义可知，ρ的大小影响着初始聚类中心的选取。由于CH-CCFDAC受到截断距离dc的影响，其不能保证距当前点的距离的点数小于dc，对于具有不同密度的数据，当采用γ=ρ·δ选择聚类中心时，类中心点与其他点之间的判别度不高，其可能导致初始聚类中心的选择失败。因此，本文从数据的整体入手，用高斯核函数来计算密度，这是本文所做的工作之一。

对每个数据点xi，采用如下的局部密度定义：

(2)

式中：dij表示数据点xi与xj之间的相似性；dc为截断距离。

初始聚类中心的选取方式类似于CH-CCFDAC算法，即先计算各点的ρ与δ值，再根据γ=ρ·δ的决策图来确定k个初始聚类中心。

CH-CCFDAC算法能够处理具有混合属性的数据集，但其不能处理具有噪声和不同密度的数据集，即带有噪声的不平衡数据集。此外，AFCM算法可以处理具有噪声与不同密度的数据集，但其不能处理具有混合属性的数据集，即具有数值属性又具有分类属性的数据集，且随机的初始化聚类中心易使其陷入局部最优。因此本文将CH-CCFDAC算法与AFCM算法进行结合，使其能够很好地处理具有不同密度、噪声以及混合属性的数据集，这是本文所做的工作之二。

因为AFCM算法是随机初始化聚类中心，若初始聚类中心与要聚类的数据点不完全匹配的话，易使其陷入局部最优且会增加时间成本。此外，AFCM算法采用欧几里得距离计算采样点与聚类中心之间的距离，若该数据集具有混合属性的话，则可能导致融合失败。鉴于此，本文首先对数据进行主成分分析，然后使用改进的CH-CCFDAC算法获得初始聚类中心，既克服了AFCM算法对初始聚类中心敏感且不能处理混合属性数据集的局限性，又解决了CH-CCFDAC算法不能处理具有噪声点与不同密度的数据集的问题。

最后利用AFCM算法基于数据点的相似性对数据进行聚类并设计了一种融合策略，即将样本数据聚为2类：正常类与异常类，并把正常类的类中心作为最终的融合值，其中正常类为更接近真实值的数据；否则，为异常类，将异常类作为故障数据，不参与融合计算，这样可有效避免误差较大的数据对融合结果的影响，以实现被划分到同一类的对象间相似性最大，类间具有较大差异性的分类目的。

1.2 HFCM算法步骤

本文提出的HFCM算法步骤如下：

Step1：对数据集进行主成分分析，计算所有数据点的相似性矩阵D=(dij)n×n。

Step2：初始化密度半径dc，根据式(2)、(3)、(4)分别计算ρ、δ、γ的值；给定参数k，去掉ρ与δ偏差较大的奇异点，并将剩余的k个点作为第1次初始聚类中心。其中距离δ={δ1,δ2,…,δn}与变量γ={γ1,γ2,…,γn}的计算公式如下：

(3)

γi=ρi×δi

(4)

Step3：给定迭代半径δ，根据改进的迭代爬山算法使Fitness值最大，以得到最优的dc，返回Step2，找到最优的初始聚类中心。其中Fitness的计算公式如下：

(5)

(6)

(7)

式中：d(xi,vj)表示xi与vj之间的距离，且d(xi,vj)=‖xi-vj‖2。

Step4：初始化聚类数目c，满足2≤c≤n；初始化迭代停止条件ε，其中ε>0；初始化阈值γ；初始化隶属度矩阵U=(uik)c×n。

Step5：t=1。

Step6：计算聚类中心和权重向量。

Step6.1：计算聚类中心。

假设隶属度uik和权重向量κ=(κ1,κ2,…,κp)是固定的，在使得损失函数达到最小的条件下，则聚类中心vi=(vi1,vi2,…,vip)按照式(8)进行更新：

(8)

Step6.2：计算权重向量

假设隶属度uik和聚类中心vi=(vi1,vi2,…,vip)是固定的，在损失函数最小的情况下，则权重向量κ=(κ1,κ2,…,κp)的计算公式如下：

(9)

式中：j=1,2,…,p。

Step7：计算隶属度矩阵

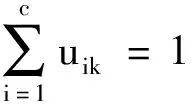
(10)

Step8：若uik的变化量小于ε，则迭代停止；否则t=t+1，返回Step3。

Step9：检查聚类的有效性，若某一类中数据点的个数小于总数据点个数的百分之γ，则该类无效，将该类中所有的点称为噪声点。

Step10：将正常类的类中心作为最后的融合结果。

2 仿真实验结果与分析

为了验证HFCM算法的有效性，本文利用UCI数据库中的2个数据集进行实验仿真，并与FCM、AFCM、CH-CCFDAC、KF[2](Kalman Filter)、RLS[2](Recursive Least Squares)算法进行对比,采用的评价指标为：运行时间(Time)、融合误差(Fusion error)、判别函数(CF)、正确率(Accuracy of correct fusion)。其中融合误差是指融合值与真实值之间的误差，本文采用欧氏距离进行度量；判别函数是指时间、残差平方和、方差之间的算术平均值；正确率是指正确融合的个数与总样本数量的比值。

实验1：采用了UCI机器学习库里的CCS(Concrete compressive strength)数据集，该数据集是由8个输入变量和1个输出变量组成。CCS数据集的总样本数量是1 030，本文采取其中的100个数据来验证HFCM算法的性能，由于这8个属性具有不同的数据级与不同的属性特征，因此需要对其主成分进行分析并归一化。

采用HFCM算法在CCS数据集上进行实验仿真，在聚类阶段将其分为2类，将正常类的类中心作为最终的融合值，并与CH-CCFDAC、RLS、KF、AFCM、FCM算法进行对比，融合误差如图1所示，各项性能指标如表1所示。

图1 6种算法在CCS数据集上的融合误差

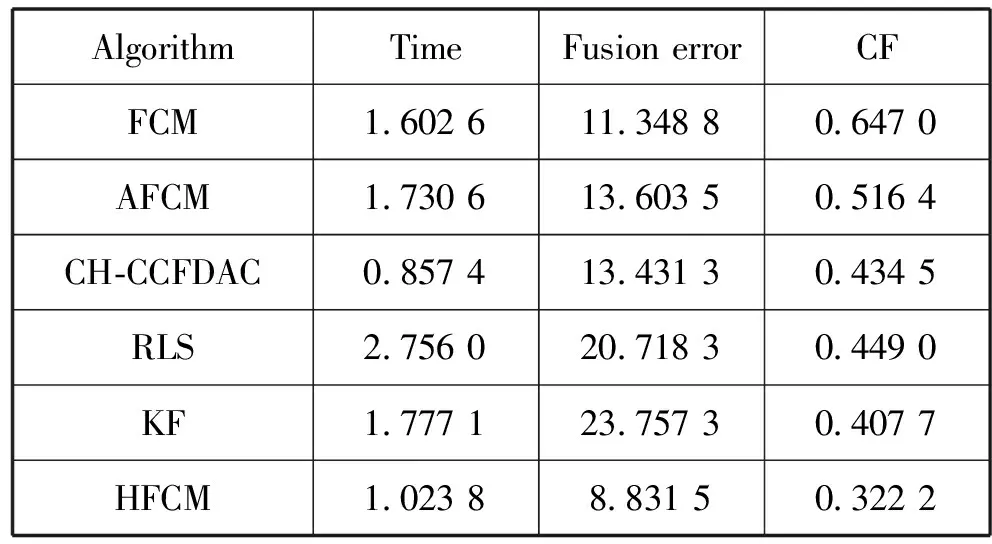
表1 6种算法在CCS上的各项指标值

从图1可看出，在这100个测试案例中，HFCM算法的融合误差的波动范围最小。从整体上看，HFCM的融合误差较小，因此HFCM的融合效果较好。从表1可看出，HFCM算法的融合误差和CF值均比CH-CCFDAC、RLS、KF、AFCM、FCM的小，表明HFCM算法融合效果较好。与FCM、AFCM算法相比较，HFCM算法的运行时间更短，因此该算法所选的初始聚类中心起着很好的作用，是可行且有效的。

为了比较融合的正确率，本文选取以真实值为中心，阈值为0.15的邻域，若融合值落在该邻域内，则表示该融合结果是正确的。6种算法在CCS数据集上的正确率如表2所示。

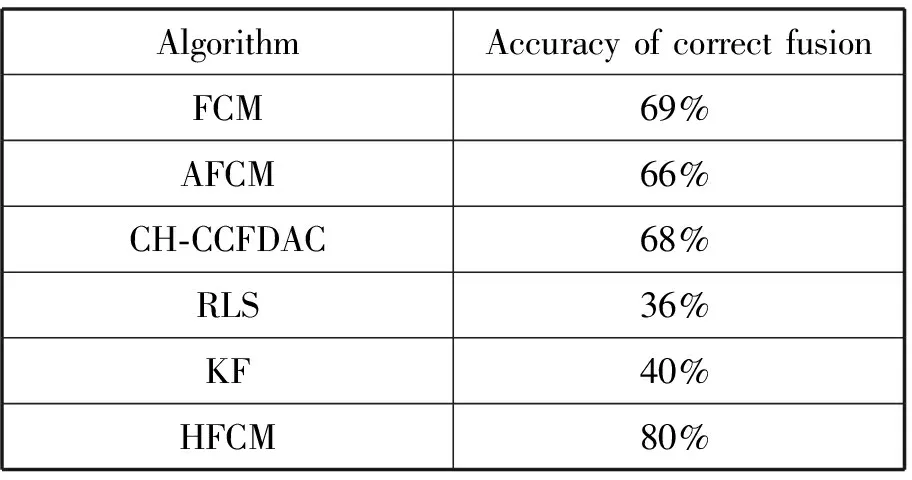
表2 6种算法在CCS上正确率

从表2可看出，HFCM算法的正确融合的精度是80%，均比H-CCFDAC、RLS、KF、AFCM、FCM算法的精度高，因此HFCM算法的融合效果较好。

实验2：采用UCI机器学习库里的Heart数据集，该数据集总共有270个数据，包括从75个较大的集合中提取的13个属性，且彼此独立，互不影响。

本文采取该数据集的55个数据来验证HFCM算法的性能。利用HFCM算法在Heart数据集上进行实验仿真，在聚类阶段将其分为2类，将正常类的类中心作为最终的融合值，并与CH-CCFDAC、RLS、KF、AFCM、FCM算法进行对比，融合误差如图2所示，各项性能指标如表3所示。

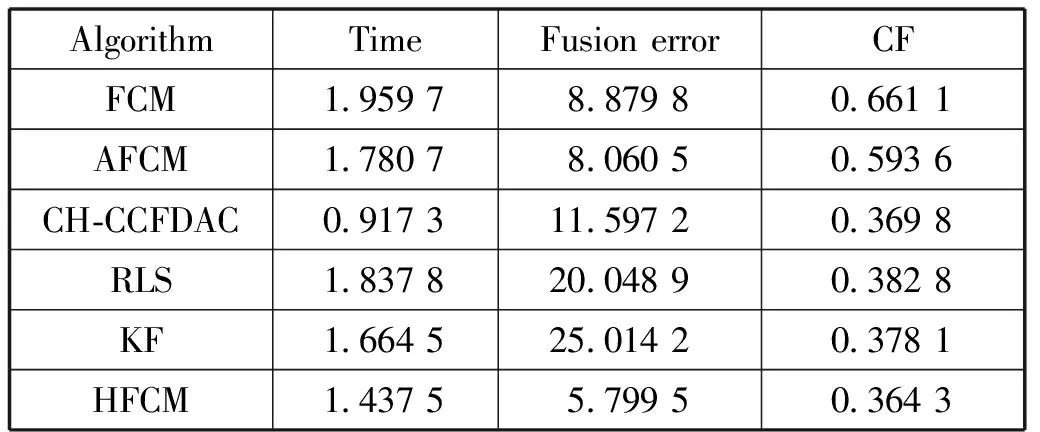
表3 6种算法在Heart数据集上的各项指标值

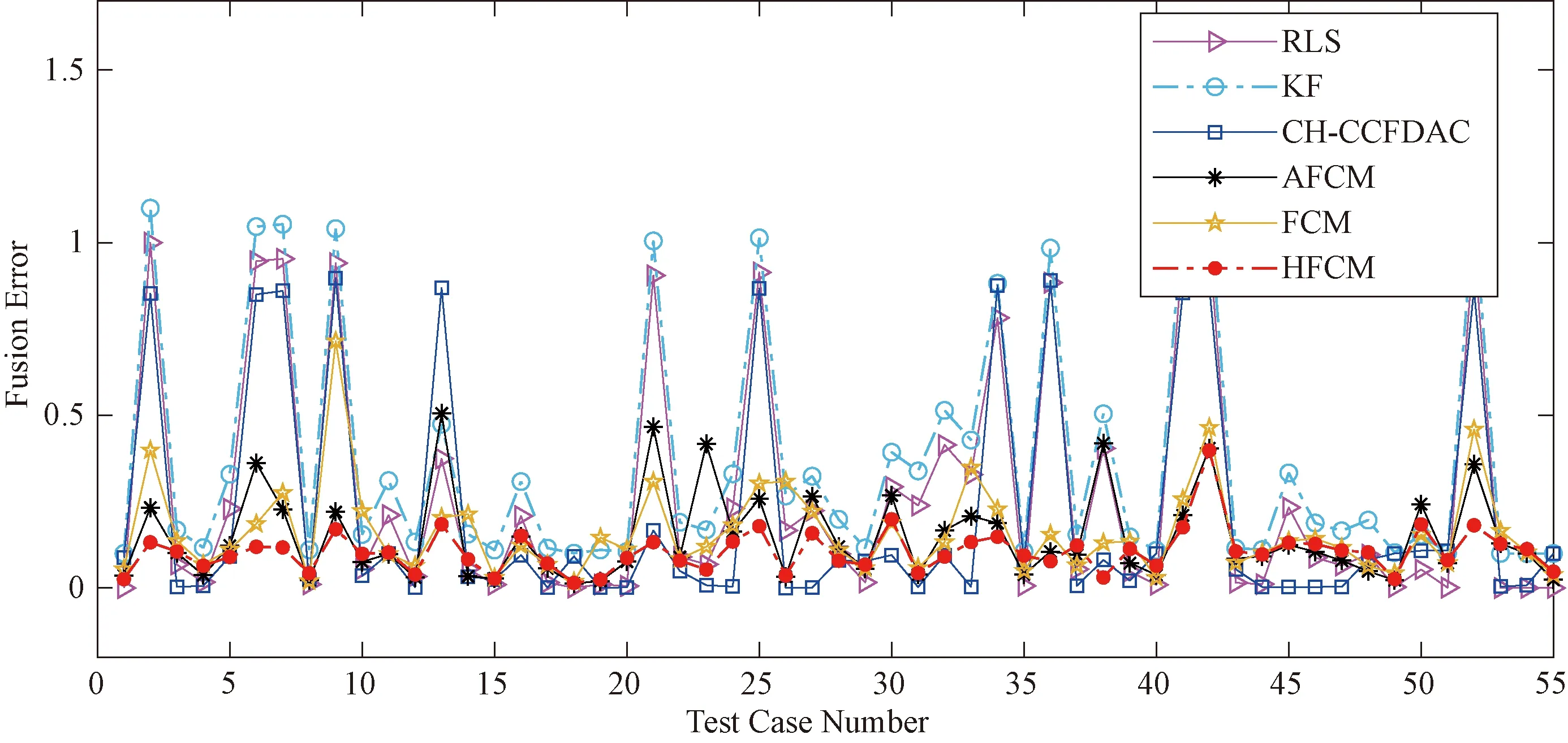
图2 6种算法在Heart数据集上的融合误差

从图2可看出，在这55个测试案例中，HFCM算法的融合误差的波动范围最小。从整体上看，HFCM的融合误差最小，因此HFCM的融合效果较好。从表3可看出，HFCM算法的融合误差和CF值均比CH-CCFDAC、RLS、KF、AFCM、FCM的小，因此HFCM算法融合效果较好。此外，HFCM算法的融合时间均较FCM、AFCM算法短，表明HFCM算法所选的初始聚类中心是可行有效的。

为了比较正确率，本文选取以真实值为中心、阈值为0.15的邻域。则6种算法在Heart数据集上的正确率如表4所示。

表4 6种算法在Heart数据集上的正确率

从表4可看出，HFCM算法正确融合的精度 82%，远高于CH-CCFDAC、RLS、KF、AFCM、FCM这5种算法，因此HFCM算法的融合效果较好，且适用于该数据集。

从实验1与实验2的融合结果中，可看出HFCM算法的融合效果要优于CH-CCFDAC、RLS、KF、AFCM、FCM这5种算法，融合的时间不仅仅取决于数据点的数量，还取决于初始聚类中心的选取。在Heart数据集上，由AFCM算法进行模糊聚类，且预聚类数量为2，其它5种算法错误融合的数量超过了本文所提算法，原因是AFCM算法随机初始化聚类中心使其陷入了局部最优，所以本文所提算法将改进的CH-CCFDAC算法与AFCM算法相结合是有效的。在CCS数据集上的融合结果也体现了这一点，初始聚类中心的选取对融合精度有很大的影响。

3 结束语

本文针对舰船的多种异质传感器基于不同的数据属性而带来的数据融合问题，提出了一种基于模糊聚类的混合多传感器数据融合算法。首先采用改进的CH-CCFDAC算法自动确定初始聚类中心且选取高斯核函数来测量具有不同属性的数据集的密度。然后，对于具有噪声的数据集，将AFCM应用于数据融合以快速实现融合。

为了测试HFCM、CH-CCFDAC、RLS、KF、AFCM、FCM算法的融合效果，本文选取了UCI机器学习库中的2个数据集进行实验仿真。为了综合比较这6种算法的融合效果，本文选取了融合误差、融合时间、正确率、CF值这4个评价指标。实验结果表明，对于UCI机器学习库中的2个数据集，HFCM算法优于文献[2]、[6]、[7]中提出的基于模糊聚类的其他融合算法，较好地解决了舰船异质传感器及其不同数据属性的数据融合问题。