恒模和相似性约束下机载MIMO雷达快速波形设计优化算法

童日武，张剑云，周青松

(国防科技大学，安徽 合肥 230037)

0 引 言

不同于地基雷达，机载雷达[1]能够有效克服由于地球曲率引起的探测盲区问题，并且具有很高的机动性，因此无论是在军事还是民事领域都得到了广泛的应用。通常情况下，机载雷达采取下视工作模式，对地面目标进行探测、跟踪、识别等等。然而大地同样能够对雷达信号进行反射形成地杂波，地杂波强度大，分布范围广，更重要的是由于机载平台的运动，地杂波的多普勒频谱范围大大展宽，这些将严重影响机载雷达对地面动目标的检测性能。因此如何采取有效的手段抑制地杂波，从而提高对地面目标的检测性能一直是一个研究的重点和热点问题。

传统杂波抑制方法主要是从雷达的接收端进行信号处理，空时自适应处理技术(STAP)是抑制杂波的有效工具，大量研究表明通过STAP技术可以显著提高雷达对地面动目标的检测性能[2]。然而机载雷达往往面临着复杂多变的外界环境，如地形的多样性导致杂波的非均匀性，干扰数量和种类的增多导致接收端处理自由度的下降等因素会严重降低STAP抑制杂波的性能。但是如果将雷达发射端的自由度加以利用，基于已知先验信息对发射端波形优化[3]，使得雷达能够根据外部环境的特点实时调整发射波形，则能够进一步提高雷达抑制杂波的能力。

多输入多输出(MIMO)雷达是一种新体制雷达[4]，相比于传统雷达具有很多优势。其最大特点是发射端具有很高的自由度，每个发射阵元可以独立发射不同的信号。MIMO雷达可分为如下两大类：一类是分布式MIMO雷达[5]，其特点是天线间距足够大，具有空间分集特性；另一类是集中式MIMO雷达[6]，其特点是天线间距很近，在波长量级，具有波形分集特性，能够在不增加雷达实际物理孔径条件下形成较大虚拟阵列，有效提高对目标的检测、识别能力，因此非常适用于空间受限的机载平台。近年来对MIMO雷达的研究得到了广泛的关注，主要包括MIMO-STAP[7]和MIMO雷达波形设计[8]等。

文献[9]研究了机载雷达发射方向图设计方法，但没有对雷达发射波形设计进行研究；文献[10]和[11]虽然研究了杂波环境下MIMO雷达波形设计问题，但所研究的对象都不针对机载MIMO雷达，文献[10]研究的是静态环境下的杂波抑制问题，文献[11]研究的是抑制距离模糊杂波问题；文献[12]和[13]虽然对机载MIMO雷达波形设计进行研究，但都只单独考虑了波形的恒模约束问题，没有同时对波形施加恒模和相似性约束，并且所使用的优化算法都是通过半正定松弛(SDR)后求解半正定规划(SDP)问题，再使用高斯随机化方法恢复出优化波形，具有较高的计算复杂度，并且使用高斯随机化方法并不能保证在迭代过程中目标函数单调非减。

针对以上文献研究的不足之处，本文基于先验信息对机载MIMO雷达波形设计问题进行进一步研究，不同于文献[12]和[13]，本文同时考虑了波形的恒模和相似性约束问题，并提出了一种快速迭代优化算法，在每次迭代过程中能够直接给出波形的闭式解，避免了求解SDP问题和使用高斯随机化方法恢复波形，具有较低的运算复杂度。

1 信号模型

1.1 目标信号

当地面目标距离机载雷达很远时，其俯仰角可以忽略不计，因此本文只考虑目标的方位角。假设目标方位角已知为θ0，对于第m个脉冲信号而言，雷达接收到的目标信号经过基带采样后可表示为：

(1)

(2)

(3)

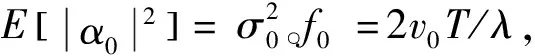
为方便计算和表示，将接收波形矩阵Yt,m向量化，有：

yt,m=vec(Yt,m)=

(4)

其中：

(5)

式中：IL表示L×L的单位阵；s=vec(S)；⊗表示克罗内克积。

(6)

其中：

(7)

式中：p(f0)=[1,ej2πf0,…,ej2π(M-1)f0]T，表示归一化多普勒频率为f0的时间导向矢量。

1.2 杂波信号

机载雷达在下视工作时会面临强地杂波的干扰，同时由于机载平台的运动，以雷达为中心的等距离环所包含的所有地杂波会存在多普勒偏移的分布，因此容易使得目标被强主瓣杂波(多普勒域)所淹没，严重影响了雷达的检测性能。因此必须通过STAP技术，从空域和多普勒域同时抑制杂波干扰。

杂波信号指的是不感兴趣的回波信号，其本质上与目标信号并无差异。本文在杂波建模的同时考虑了目标所在距离环[14]的杂波信号以及目标相邻距离环的杂波信号。

图1画出了3个杂波距离环，分别为目标所在距离环以及目标前后的距离环。将每个等距离环内的杂波看成为若干等份杂波块的组合，因此杂波信号可以表示为所有杂波块信号的叠加。

图1 杂波距离环

以目标所在距离环为参考标准，对于第r(r=0表示目标所在距离环；r>0表示目标后面距离环；r<0表示目标前面距离环)个距离环而言，假设共有Nc个杂波块，则其第k(k=1,2，…,Nc)个杂波块相对于第m个脉冲信号而言的杂波信号可表示为:

(8)

式中：αc,r,k，fc,r,k，θc,r,k分别表示距离-角度位置为(r,k)的杂波块对应的幅度，归一化多普勒频率，方位角。

(9)

式中：r∈{0,±1,±2,…}；(m,n)∈{1,2,…,L}2。

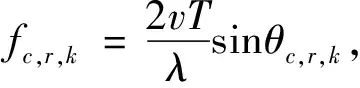
(10)

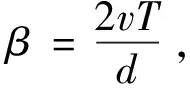
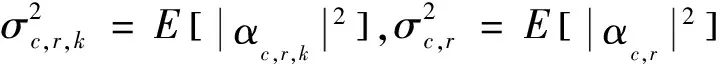
αc,r,kA(r,fc,r,k,θc,r,k)s

(11)

其中：

(12)

当r=0时，Jr=IL,则对于目标有A(f0,θ0)=A(0,f0,θ0)。为方便表示和运算，将A(f0,θ0)表示为A0，将A(r,fc,r,k,θc,r,k)表示为Ac,r,k。

则对于2R+1个杂波距离环而言，总的杂波信号表示如下：

(13)

雷达接收机接收到的总信号为目标信号，杂波信号以及接收机内部噪声的叠加，即：

y=yt+yc+n=

(14)

2 问题阐述

2.1 最大化输出SINR

雷达接收机接收到回波信号后需要对信号进行处理以提高检测性能，而SINR是衡量检测性能的一项重要指标，SINR越高意味着发现概率越高，因此本文以最大化输出信号的SINR为优化准则进行波形设计。

yout=wHy=

(15)

故输出SINR表示为：

RSIN(w,s)=

(16)

2.2 恒模和相似性约束

在工程实践当中，雷达发射机放大器通常工作在饱和状态，无法对波形幅度进行调制，因此为了能够充分利用发射机放大器放大功率，往往要求发射的波形具有恒模特性。本文对波形施加恒模约束，为方便表示和计算，假设波形具有归一化发射能量，即‖s‖2=1，那么波形s的第i个元素s(i)表示如下：

(17)

式(17)又可表示为：

(18)

式中：φi表示si的相位。

对波形施加相似性约束可以使得波形享有已知参考波形的良好特性[16]，如线性调频信号具有良好的脉冲压缩特性和理想的模糊度特性。相似性约束的本质是在已知参考波形的邻域寻找合适的解，表示如下：

(19)

式中：s0表示已知参考波形，且有‖s0‖2=1；s0(i)表示波形s0的第i个元素；ε(0≤ε≤2)表示相似度，当ε=0时，s(i)=s0(i)；当ε=2时，不存在相似性约束，退化为恒模约束。

由于同时施加恒模约束和相似性约束，s(i)只有相位上的自由度，式(19)可进一步表示为[16]：

φi=args(i)∈[γi,γi+δ],i=1,2,…,NTL

(20)

其中：

γi=args0(i)-arccos(1-ε2/2)

(21)

δ=2arccos(1-ε2/2)

(22)

由以上设计指标和约束条件，可得以下优化问题：

(23)

忽略目标函数中的常数项不影响优化结果，则有:

(24)

3 优化算法

优化问题(23)是一个NP-hard问题，无法在多项式时间内给出最优解，但可以通过优化算法获得其高度近似解。文献[12]、[13]在求解只有波形恒模约束的优化问题时所使用的优化算法都是通过循环迭代w和s，在每次迭代过程中都需要求解SDP问题，并需要使用高斯随机化方法恢复出优化波形。然而该算法存在以下几点不足：一是由于求解SDP问题并使用高斯随机化方法恢复出秩1约束的波形近似解，计算复杂度较高；二是使用高斯随机化方法不能保证在迭代过程中目标函数单调非减。

考虑以上文献中算法的缺点，本文提出了一种新的迭代算法，不需要循环迭代w和s，且能够避免求解SDP问题和使用高斯随机化方法获得波形的近似解，在每次迭代过程中能够直接给出波形的闭式解，具体算法如下。

当固定s时，问题(24)转化成如下无约束优化问题：

(25)

其中：

Rcn(s)=Rc(s)+INRLM

(26)

(27)

问题(25)等价于如下著名的最小方差无失真响应(MVDR)问题[17]：

(28)

其闭式解如下：

(29)

由上可知wopt和s之间的关系，将式(29)代入到式(23)中，经过一番整理后得到如下优化问题：

(30)

观察可发现分式规划问题(24)已经被转化成一个非分式规划问题。

令：

(31)

则第l次迭代过程中，问题(30)转化成如下优化问题：

(32)

首先抛去约束条件，可得：

(33)

由类功率迭代法[18]易知其具有归一化能量的波形闭式解为：

(34)

求得s后再考虑恒模约束和相似性约束，可得：

(35)

式中：φu(i)表示u(sl)的第i个元素的相位；∃m∈{-1,0,1}。

求得φi后，由式(18)可求得s(i)。

算法总结如表1所示。

表1 本文提出的算法

对于文献[12]、[13]中算法，在每次迭代过程中更新一次w的计算复杂度为Ο((NRLM)3),解一次SDP问题的计算复杂度为Ο((NTL)3.5)，使用高斯随机化恢复s的计算复杂度为Ο(P(NTL)2),P表示随机化次数。故该算法每次迭代总的计算复杂度为：Ο((NRLM)3)+Ο((NTL)3.5)+Ο(P(NTL)2)。

对于本文所提的算法，在每次迭代过程中只需要更新一次u(s)，计算复杂度为Ο(NTL·(NRLM)2)。

综上可以看出，本文所提出的算法具有更低的计算复杂度。

4 仿真分析

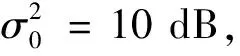
S0(m,n)=

(36)

式中：m=1,2，…,NT；n=1,2,…,L；s0=vec(S0)。

4.1 本文算法和文献[12]中算法2性能比较

表2给出了2种算法在只考虑恒模约束情况下的性能指标，包括SINR(dB),CPU运行时间time(s)，迭代次数l，图2给出了2种算法的SINR随迭代次数的变化曲线。

表2 本文算法和文献[12]算法性能比较

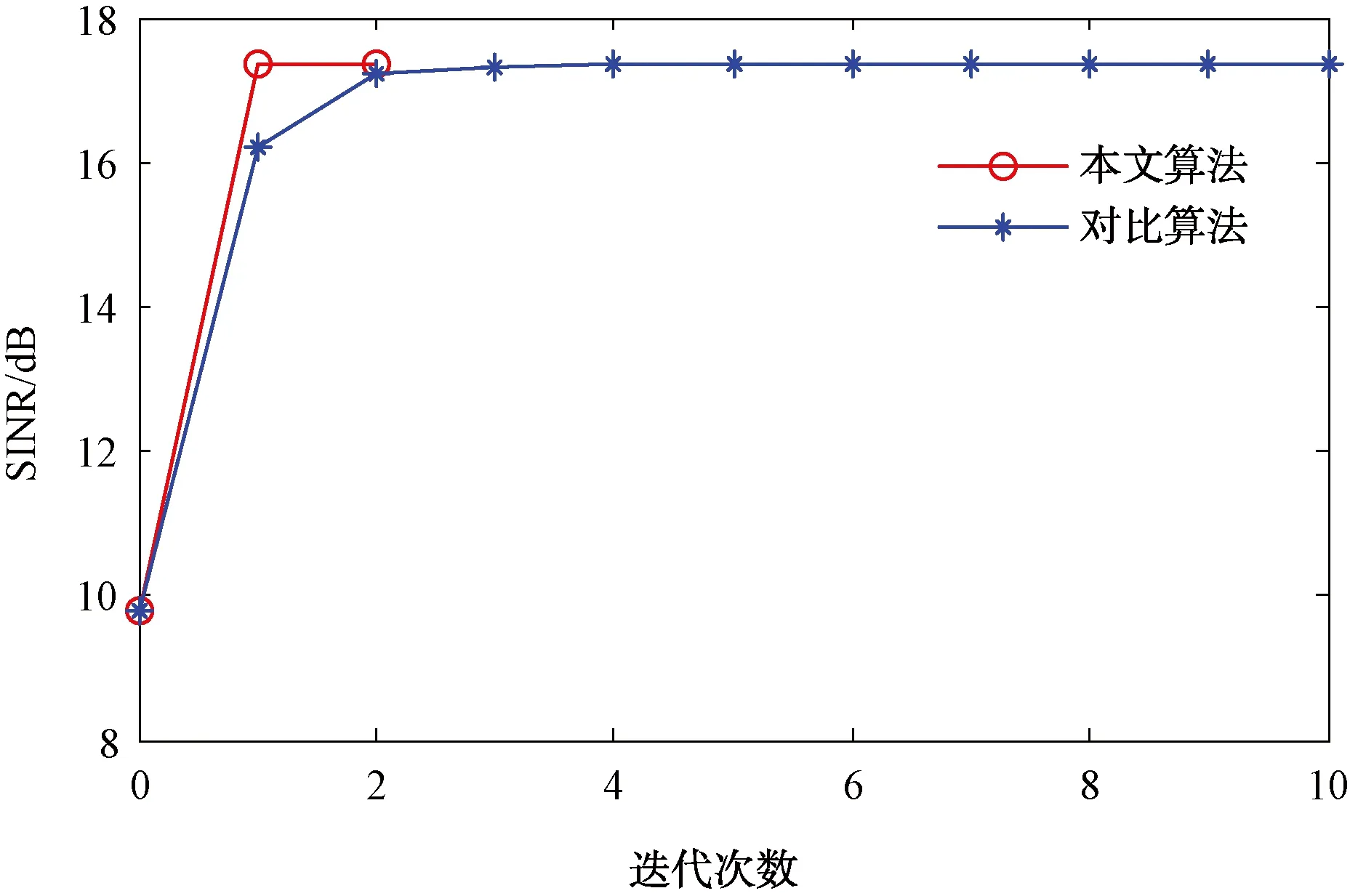
图2 2种算法SINR随迭代次数变化曲线

从表2和图2可以看出，在只考虑恒模约束时本文所提算法比对比算法的SINR略高,并且本文算法的运算速度更快，仅需要2次迭代即可停止，耗费时间为24.398 2 s,而对比算法则需要10次迭代才能够停止，耗费时间为187.457 3 s。从对比结果可以看出，本文算法不仅和对比算法具有相同的优化效果，而且具有更快的运算速度。

4.2 相似度对SINR的影响

表3给出了相似度ε=2,0.5,0.1时使用本文算法得出的优化结果。

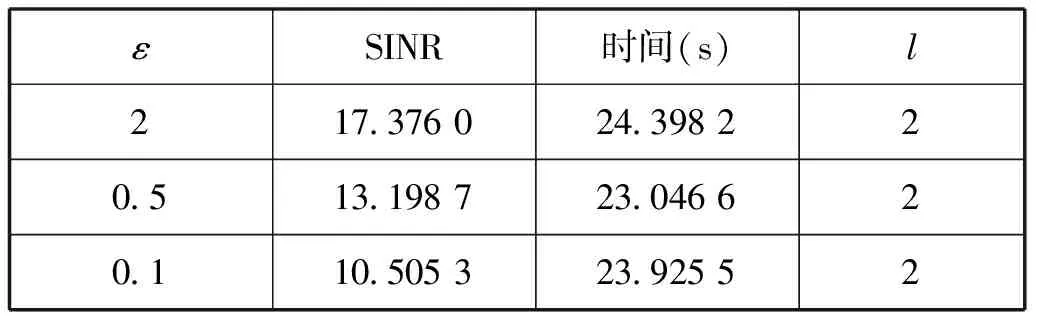
表3 相似度对SINR的影响

从表3中可以看出，随着ε的减小，优化后的SINR也不断减小，这是符合理论预期的。因为ε的不断减小，意味着波形s的可行集在不断减小，从而导致相位的自由度越来越低，最终体现为优化后的SINR值不断降低。另外从表3中也可以看出无论ε取何值，该算法都具有很快的运算速度。

图3给出了在ε=2,0.5,0.1时SINR随迭代次数的变化曲线。从图3中可以看出波形优化后的SINR由最初未波形设计时(即使用参考信号S0)的9.773 3 dB得到了较大幅度的提升。特别在ε=2时，SINR提高了将近7.5 dB。

图3 不同相似性约束下SINR随迭代次数变化曲线

4.3 波形性质分析

图4给出了优化波形的幅度曲线，从图中可以看出，无论相似度取多少，优化后的波形振幅恒定，说明了本文算法所设计的波形能够满足恒模约束的要求。

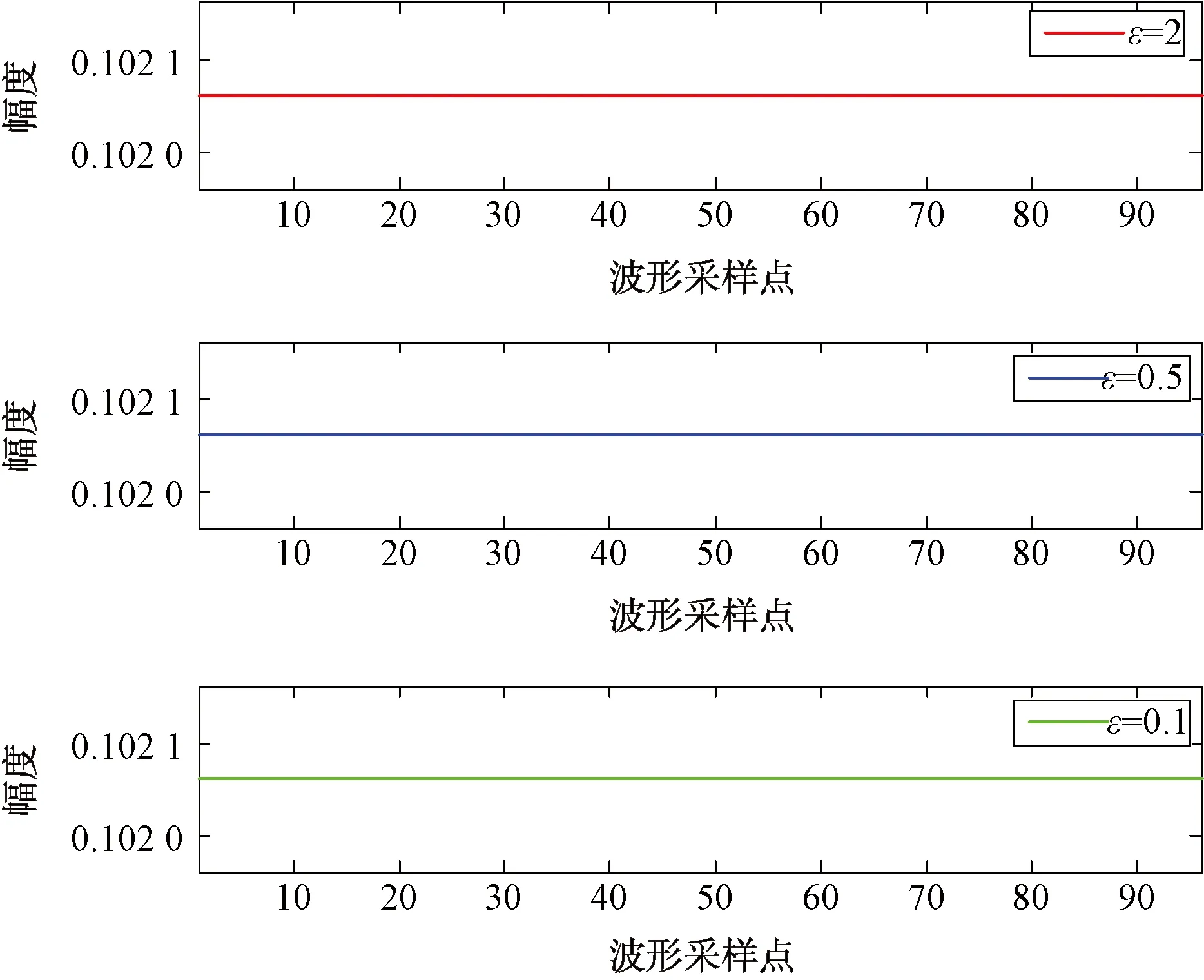
图4 波形幅度

图5给出了在ε=2,0.5,0.1时雷达第一个发射阵元对应的发射波形的脉冲压缩特性曲线图[10]。

图5 波形脉冲压缩特性曲线

从图5可以看出，随着ε的减小，脉压旁瓣水平不断下降，越来越接近于参考波形LFM的脉压旁瓣，说明了本文算法能够对波形起到相似性约束的效果。

4.4 杂波抑制效果分析

最后，本文给出了在ε=2，r=0时空-时互模糊函数的二维响应图，分析了波形优化后对杂波的抑制效果。空-时互模糊函数定义如下：

P(r,f,θ)=|wHA(r,f,θ)s|2

(37)

从图6可以看出，在目标位置形成峰值，在杂波脊位置形成一条深零陷，说明了本文算法能够有效抑制杂波。

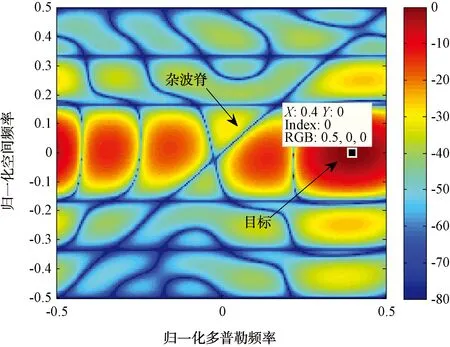
图6 空-时互模糊函数二维响应图

5 结 论

本文研究了机载MIMO雷达在强地杂波环境下的波形设计问题，进一步提高了雷达抑制杂波的性能。本文对波形同时施加了恒模约束和相似性约束，并提出了一种有效的快速迭代优化算法。仿真结果表明了本文所提算法能够有效提升SINR,进一步增强了对杂波的抑制能力，并且该算法具有较低的运算复杂度，所设计的波形具备恒模特性和相似性特点。下一步可能的工作是研究在杂波兼频谱拥挤环境下机载MIMO雷达的波形设计问题。