对数导数及其应用

陆天虹

（上海立信会计金融学院，上海 201209）

导数理论的应用非常广泛，作为函数基础理论的深化和应用，产生了新的导数定义，如方向导数、列导数和对称导数等。国内外许多经济金融实证分析表明，需要将绝对数据转换为相对数据，特别需要考虑数据的可用性，诸如数据应用的稳定性、数据的厚尾现象以及消除数据的异方差等，至于大数据时代尤为重要。作为导数理论的推广，我们首次提出双对数导数的概念，利用单对数导数和双对数导数定义弹性和成长等相关概念，从而揭示对数导数理论和相关弹性理论以及统计模型理论等的联系和内在规律。

一、对数导数

导数有许多定义，列导数、对称导数以及方向导数等，本项目中我们所称的对数导数含单对数导数和双对数导数。

一阶单对数导数就是一般的对数导数。设正函数f(x)定义在

[a，b]上，f(x)∈C1，定义L(x)=L1(x)=f'(x)/f(x)为f(x)的一阶单对数导数；

若f(x)∈C2，则称L2(x)=f''(x)/f'(x)为f(x)的二阶单对数导数；类似可定义其各高阶单对数导数（注：定义中各阶导函数不含零点，正函数可通过绝对值运算推广为非零函数，以下同）。

双对数导数的定义：设正函数f(x)定义在[a,b](a＞0)上的C1类函数，对x∈[a,b]，定义下列极限

为f(x)的一阶双对数导数（假设极限存在，注：双对数非重对数），记为E(x)(E1(x)=E(x))；同样也可定义f(x)的各高阶双对数导数En(x)=xLn(x)（注：定义中区间[a,b]可通过绝对值运算推广为任意区间，如含原点则需要分子区间讨论）。对多元函数可类似定义相关偏导数。

二、弹性和成长

（一）弹性函数和成长函数的定义

在经济金融理论以及实证分析中，经常考虑到变量之间的弹性关系。变量之间的弹性关系揭示了一种变量对于另一种变量的微小百分比变动关系。

定义2.1 称函数L(x)=f'(x)/f(x)为f(x)在[a,b]上的绝对弹性函数（或系数），并记EA(x)=L(x)；称函数为f(x)在[a,b]上的（相对）弹性函数（或系数），并记ER(x)=L(x)。

定义2.2 称函数L2(x)=f''(x)/f'(x)为f(x)在[a,b]上的绝对成长型投资函数（或系数），并记GA(x)=L2(x)；称函数为f(x)在[a,b]上的（相对）成长型投资，简称成长函数（或系数），并记GR(x)=E2(x)。

（二）线性化

定理1.函数f(x)的弹性可线性化的充要条件是函数可表示为指数函数和幂函数的乘积型。

统计学中，当且仅当变量服从指数型或幂率分布或两者乘积型分布时，建议采用双对数变换模型。

定理2.个体效用函数揭示二基金资产分离成长型的充要条件是该效用函数的成长系数的倒数可线性化。

投资者在风险资产组合和无风险资产之间投资组合配置时，如果个体效用函数满足其成长系数的倒数呈现线性化，那么可考虑二基金资产分离成长型投资决策。

负指数效用函数

幂效用函数

（0.5）f(x)Ýx=x0处可导C记为f(x)∈Dx=x0

f(x)∈Dx=x0⇔f(x)在x0处左、右导数存在并相等，即f(x)∈Dx=x0⇒f(x)∈Cx=x0,反之不成立，如

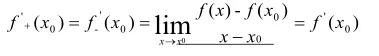
反例：f(x)=|x|,f(x)∈Cx=0,但f(x)∉Dx=0.

若∀x∈I(⊆D),有f(x)∈Dx，则称函数f(x)在I上 可导（或在I上存在一阶导函数f'(x))，同时记f(x)∈D，且有I

f(x)∈DI⇒f(x)∈CI.

注：f(x)在端点处的可导定义为f(x)在该端点的一个单侧导数存在

(1)f(x)在I上一阶连续可导，记为f'(x)∈CI

若f(x)在I上存在一阶连续可导函数，我们就称f(x)为第一类

光滑函数，记为f(x)∈C1(或C1I).

（1.5）f(x)Ýx=x0处二阶可导C记为f(x)∈D(2)x=x0（或D''x=x0）

f(x)∈D(2)x=x0⇔f'(x)在x0处可导，即

若∀x∈I(⊆D),有f'(x)∈D，则称函数f(x)在I上 二阶可导（或x

在I上存在二阶导函数f''(x))，同时记f(x)∈D(2)，且有I

f(x)∈D(2)I⇒f'(x)∈CI.

(2)f(x)在I上二阶连续可导，记为f''(x)∈CI

若f(x)在I上存在二阶连续可导函数，我们称f(x)为第二类

光滑函数，记为f(x)∈C2(或C2I).

三、对数导数的意义

（一）一阶对数导数的意义

（二）二阶对数导数的意义

研究表明，个体投资者其效用函数揭示二基金资产分离成长，当且仅当其效用函数的近似曲率半径呈现线性化。个体效用函数类属二次函数、负指数函数、狭义幂函数以及广义幂函数时，其对应的近似曲率半径是线性函数，因此相应的个体投资者资产配置呈现二基金资产分离成长型。进一步研究表明，随着近似曲率的定义逐步趋向曲率（复杂化），研究个体投资者效用函数的范围越来越广泛，投资者的资产配置将更加工程化精细化。

表1 内在联系和规律

表1续：

设解释变量x由观察得到，记x0=E为真值，被解释变量y由拟合函数y=f(x)给出。若已知观察样本x的 误差限为δx，即|Δx|=|x-x0|≤δx，则当δx很小时，|Δy|=|f(x)-f(x0)|≈|(x0)Δx|≤|(x0)|δx=δy,δy称为被解释变量y的误差限，而y的 相对误差限则定义为

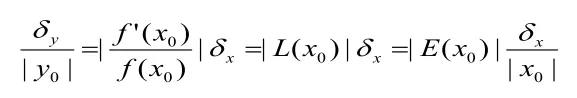
误差估计

该式表明被解释变量的相对误差限在解释变量的误差限基础上被扩大了|L(x0)|倍（以对数导数或绝对弹性系数为杠杆系数），同时两个变量各自的相对误差限之比正好是（相对）弹性系数。

进一步我们也可以得到（考虑二阶展开）：

四、对数变换

我们在研究被解释变量和解释变量的关系时，经常要考虑到变量之间蕴含的相互关系，绝对数据转换为相对数据（如环比数据等），消除数据之间的异方差性，以及将变量的指数趋势转变为线性趋势等，因此有必要对变量引入对数变换。统计研究中，对数变换处理数据主要分单对数变换法和双对数变换法。（1）单对数变换法。该对数变换法主要是单独对解释变量或被解释变量采取对数变换，是数据拟合中常用的方法。经典情形如：我们发现解释变量呈现偏态分布，如果对其数据进行对数变换后服从正态分布，这就是经典的具有再生性的对数正态分布。如果考虑对纵坐标进行对数变换，则预期获得较好的效果。（2）双对数变换法。该对数变换法是对解释变量和被解释变量均进行对数变换处理。对数变换应用比较广泛，在前述对数导数理论的基础上，关于对数变换我们得到了新的认识，以下对双对数变换给出一个简单模型。

如果各解释变量和被解释变量之间存在着可线性化的弹性关系，那么根据前述定理，我们采用双对数线性回归模型进行分析。考虑幂函数（或指数函数或两者乘积型）关系型：

于是，经过双对数变换，建立总体模型如下：

lny=lna0+a1lnx1+a2lnx2+…+anlnxn+lnε0

lny=lna0+a1lnx1+a2lnx2+…+anlnxn+ln[1+ε0/E(y)].

我们知道，许多经济变量之间相互表现为可线性化（或拟线性化）的弹性关系。著名的Box-Cox变换可看作单对数变换和幂效用函数类型。经济金融以及统计分析中，效用函数常表现为幂函数或（负）指数函数型。从统计角度而言，多数变量采样数据相对而言更接近对数正态分布。因此，我们在研究变量之间相互关系时，如果解释变量和被解释变量之间蕴含可线性化的弹性关系，那么根据双对数导数概念以及前述定理，可以考虑对变量采用双对数变换进行处理，建立双对数变换模型。