三角函数及其图像在物理学中的应用

温昊翔

（惠州市榕城中学，广东 惠州 516000）

前言：三角函数的知识被广泛的应用在了物理学当中，这是由于物理学研究的对象大都是矢量，运算矢量使不仅要考虑到其大小，还要考虑到适量的方向，这时就必须使用到三角函数知识了。较为常见的处理适量的方法就是正交分解或三角形法则，这些法则都需要三角函数知识理论的支撑。

一、简述三角函数及其图像

较为常见的三角函数如下：y=sinx，y=cosx，y=tanx，y=cotx。公式中的自变量的单位是弧度[1]。在学习物理知识与解析物理题的过程当中，经常会用到三角函数的知识，尤其是正弦函数与余弦函数。下面对正弦函数、余弦函数和它们的图像进行解析。

正弦函数与余弦函数都是周期函数，并且周期都是2π。正弦函数的图像如图一所示，是奇函数，其在坐标系内的图形以原点为对称。正弦函数的图像如图二所示，是偶函数，其在坐标系内的图像以y轴为对称。

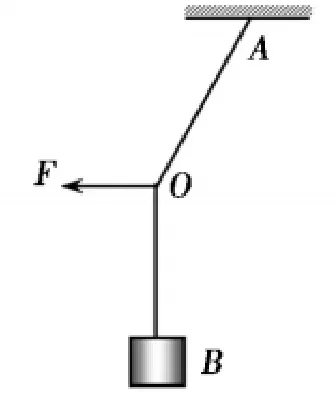
图一：物体的动态平衡

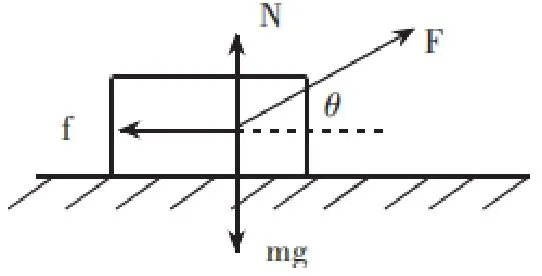
图二：土块匀速运动

二、三角函数及其图像在物理学科当中的应用

三角函数阐述除了直角三角形当中三个边与各个角存在的关系，为物理量之间创造了关联[2]。因此我们在解题的过程当中，一般都是以函数具有的特征、变化规律的知识为基础进行运算，得出物理量的变化趋势、求解值等。

以几道例题作为例子，阐述三角函数及其图像在物理学科当中的应用[3]。

1、基于函数的增减性，分析物理量产生的变化

例1一个物体的质量为m，m被轻绳AB悬挂在天花板之上。我们此时用水平向左的力F来缓缓地拉动轻绳的中点O，情况如图三所示。用Y代表绳子OA段受到的拉力大小，在O点在移动的过程当中，F于Y产生了怎样的变化？

习题解析：把OA段与竖直方向的夹角设为α，重力加速度是g，则平衡条件如下所示：

角度α随着O点的移动而不断增大，tanα是增函数，F呈增大趋势；cosα是减函数，Y呈增大趋势。

总结：在解析诸如此类的动态平衡问题时，要以函数的增减性为基础，来判断力产生了怎样的变化，是最为基础的力学问题之一，并且，也可以使用矢量图来观察力的变化。

2、基于函数的变化规律计算物理量的最值

例2 如图四所示，一个质量为m的小方块以静止状态在水平面上，以一个大小为F的恒力拉它，让方块在水平面上做匀速直线运动。设F与水平面的夹角为θ，在夹角θ逐渐向90度变化时，F会发生怎样的变化？（物体与水平面之间的摩擦系数已知，为μ）

习题解析：力的平衡条件如下：

Fcosθ=μ（mg-Fsinθ）

总结：例如acosθ+bsinθ此类的三角函数，把a、b作为直角边构造出一个辅助三角形，将其转化为sin（α+θ）或者是cos（α+θ），然后对极值进行运算。

3、根据函数的性质进行近似计算

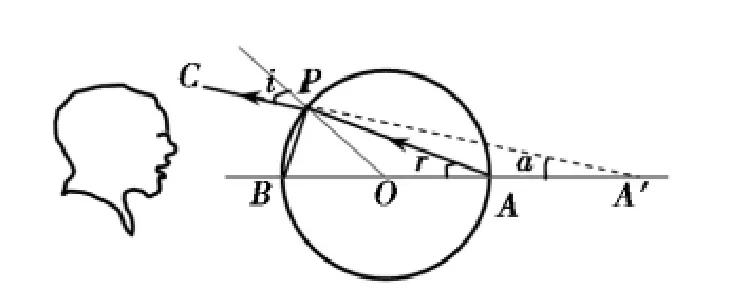
图三：光路图

例3 如图所示，一个玻璃球内装满了水，其厚度可以忽略不计，设该球体的直径d为12cm，已知水的折射率求沿着水平方向观察该球体的直径数值。

习题解析：人的视线沿着球体的直径方向看去，以肉眼不能够目测其长度。也就是说，用人眼来对直径进行测量时，得到的结果是不准确的，会与实际数值发生一定的偏差。从图中我们可以看出，P点与B点的距离十分进，从A点射出的光纤，以P点为折射点折射到空气当中，PC这条线是折射到空气当中的光纤，人眼是逆着PC线观察到的A点，也就是A’点，也就是说A’B的距离就是我们要进行计算的。

该题中的法线也就是OP线，PB长度较短，则角i、r与α的角度都很小。基于几何知识，α+（i-r）=r，可以得出α=2r-i。PB=ABsinr，因此PB=A’Btanα。基于折射定律，sini=nsinr，在角i、r数值小时，可以得到i=nr。这样得出水平方向看球体的直径公式如下：

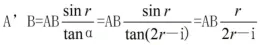
在带入已知的直径12厘米数据等，求得A’B的数值为18厘米。

总结：我们在进行物理习题的解析式，运用三角函数，要合理的进行近似与取舍。

结语：综上所述，我们在进行日常物理习题的计算当中，经常会应用到数学知识点，尤其是三角函数的知识，在解题过程中能够得到广泛的使用。本文主要介绍了正弦函数、余弦函数在物理学当中的应用。经过对例题进行解析和判断，证明了三角函数在解析物理习题时有着重要的作用。