基于PageRank算法的出租车需求预测

周丰

(上海大学 通信与信息工程学院， 上海 200072)

0 引言

智慧城市作为实现城市资源的智能分配和科学管理的重要手段[1-2]，有利于解决城市交通问题。目前城市的交通问题之一是出租车司机与乘客面双向面临着接客难与打车难的问题，出租车的合理分配问题[3]亟待解决。

随着嵌入式和传感器设备的发展，城市中大量移动物体的轨迹已变得越来越容易获得[4]。例如，中国的许多出租车公司为了管理目的需要会在每辆出租车上安装GPS设备，这为记录出租车当前以及历史轨迹提供了基础设施。通过出租车轨迹数据可以知道，站点的流量状态不是独立演变的，会受到临近站点流量状态的影响，因此可以把交通系统看成复杂网络[5]，来研究城市出租车系统中的人群流动模式[6-8]，从而发现出租车分配的更好方法。此前研究发现[9]，利用Google最初开发的PageRank算法可以从动态的角度对城市交通演化进行建模，更深入的了解城市动态。

本文研究贡献在于：

1.利用PageRank建模[10]时，把城市热点区域作为节点，以此解决数据分区和网格分辨率对模型带来的影响。

2.不仅利用ARIMA模型[11-12]预测热点区域的乘客数量，而且还发现动态特征PageRank值与预测乘客量间的确定性关系。

3.根据北京市10000辆出租车轨迹数据实验验证结果的准确性。

2 数据处理

2.1 数据

我们用于实验的数据来自北京地区的10000出租车部分轨迹数据，如图1所示。

数据主要来自2014年4月1日至15日，包含4个假期，2个周末和10个工作日。 在实验期间， 15天的数据被分为3组，分别对应假期，工作日和周末；同时，一天的数据分为3个不同的时间段：上午高峰时间(6：00-10：00)，工作时间(10：00-16：00)和晚上高峰时间(16:00-20：00)。 由于20:00 PM - 6:00AM时间段内流量很少发生，因此在考虑PageRank值和ARIMA预测值之间的关系时，不考虑这段时间。

图1 北京城区部分出租车轨迹图

计算热点区域交通状态时，我们以15分钟作为时间间隔，每天有96个时间间隔，热点提取时使用前10天的数据，后五天的数据被用来对模型进行预测准确率的验证。

每辆出租车都配有GPS设备，以约每60秒一次的采样频率记录出租车的轨迹，其中包括以下项目：

TAXI_ID：出租车的唯一ID;

GPS_TIME：采样时间戳;

GPS_LONGITUDE：出租车当前经度；

GPS_LATITUDE：出租车当前纬度;

GPS_STATUS：GPS设备的当前状态，有效或无效，表示来自GPS设备的消息是否成功。

METER STATE：表示计程表是否正在运行，即出租车是否有乘客：如果出租车被占用，则为1；如果是空闲，则为0。

2.2 数据处理

由于GPS信号和设备故障的多路径效应，GPS位置有时可能不正确。此外，由于驾驶员做出的无效操作，METER STATE也可能不正确。例如，当一个出租车司机下班时，尽管出租车中没有乘客，但他们可能会打开计程表。为了阐明真实的空置轨迹和占用轨迹(分别有无轨迹)，数据预处理如下：

我们对持续时间和平均速度超出正常范围的占用轨迹进行过滤。分析了占用轨迹的持续时间和平均速度的分布。平均速度范围设定为5米/秒至40米/秒。 所有不符合这些条件的占用轨迹都将被视为无效。此外，也删除了包含具有明显的经度或纬度的不正常的记录。

3 PageRank流量建模

3.1 热点提取

热点是频繁出现上下车事件的区域，如图2所示。

图2 规定阈值后热点图

本研究将热点作为节点进行复杂网络建模，所以首先进行热点提取，出租车记录中METER STATE的转换被视为上/下车事件，即从0到1的METER STATE变化表示上车事件(PUQ)，并且METER STATE in从1到0的转换指示一组下车事件(SDQ)，连续的0或1表示为空载或已有乘客。热点提取步骤如下：

(1) 从10 000辆出租车随机选取100俩抽样分析。

(2) 从轨迹数据提取转换事件，记录事件数量。

(3) 设置热点阈值，根据阈值提取出明显的热点。如图3所示。

(a)

(b)

3.2 PageRank流量建模

显然，每个地区上/下车的状况都受到邻近地区的影响，出租车经常在这些热点之间来回行驶，而这些行驶轨迹可以看成是连接这些热点的链接。在这里，我们采用PageRank方法来研究整个网络的动态行为。PageRank算法最初被Google用来根据网页中的引用排列网页的流行度。在PageRank算法中，网页的受欢迎程度根据引用此页面的网页的得分进行评分，其中由网页贡献的分数被平均分配给此页面引用的页面。所有页面的最终获得的分数用于排列它们的流行度。由于交通系统可以建模为复杂的网络，因此我们利用PageRank对热点的“流行度”进行排序，并研究PageRank值的规律。直观地说，“受欢迎的地区”或中心有很高的可能出租车需求量大。在以热点为节点的城市交通复杂网络模型中，一个热点向邻近热点提供交通流量，热点间交通流量的传递对热点影响的传播与PageRank机制相似。因此，PageRank算法用于量化出租车需求是可行的。

我们以北京为例，表明一个城市可以划分为热点区域。如果车辆从一个热点前往相邻区域，则意味着应该有连接这两个热点的道路，并且通过两个热点的交通流作为连接它们的定向链路。图3(a)和(b)给出了网络模型的一个概念性例子。以热点作为节点和交通流作为连接区域的链接，城市的交通系统可以建模为时间复杂的网络，其中动态链路通过时间相邻热点之间的交通量加权。

时间t处的热点i的PageRank指数被定义为式(1)。

(1)

其中N(t)是所有热点的数量，NR(i)热点i周围的邻近热点，有流量将它们连接到热点i，Pj(t)是热点j的PageRank指数，Oji(t)表示t时刻从热点j到热点i的交通流量，∑Oj(t)在时间t时所有流出热点j的流量，d=0.85是固定系数，以避免陷入没有流出的区域。 当两个连续迭代之间的PageRank值之差小于0.000 001时，算法停止。

为了更好地观察，Pi(t)量化到1到 10，如图4(a)，在时间t的最大值和最小值之间有10个相等的间隔。

4 ARIMA人群流动性预测

ARIMA (Auto Regressive Integrated Moving Average) 被广泛用于对时间序列进行预测，常被用于需求预测和规划中。不过，如果是从一个非平稳的时间序列开始，首先需要做差分，直到得到一个平稳的序列。模型的思想就是从历史的数据中学习到随时间变化的模式，学到的规律去预测未来。

ARIMA包含3个部分，即AR、I、MA。

AR：表示auto regression，即自回归模型；

I表示integration，即单整阶数，时间序列模型必须是平稳性序列才能建立计量模型，ARIMA模型作为时间序列模型也不例外，因此首先要对时间序列进行单位根检验，如果是非平稳序列，就要通过差分来转化为平稳序列，经过几次差分转化为平稳序列，就称为几阶单整。

MA：表示moving average，即移动平均模型。可见，ARIMA模型实际上是AR模型和MA模型的组合。

本研究中，PUQ{PUQi,i=1,2,…,N}为给定热点中上车事件时间序列，可将ARIMA模型的输入设置为{PUQi,i=1,2,…,N-1}，输出是PUQN，即乘客流量预测值。建立模型一共分为3部。分别介绍如下。

4.1 将非平稳序列转化为平稳序列

一个时间序列的随机变量是稳定的，当且仅当它的所有统计特征都是独立于时间的(是关于时间的常量)。稳定的数据是没有趋势(trend)，没有周期性(seasonality)的。如果一个时间序列是不稳定的，那么预测前需要对改序列进行求和操作，转换成一个稳定序列，如式(2)。

(2)

d是差分的阶数，可以用单位根测试估计获得。

4.2 自回归(AR)

自回归模型(Autoregressive Model)是用自身做回归变量的过程，即利用前期若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型，把时间序列PUQ的预测值表示为时间序列的历史值和一个随机白噪声et的组合：

PUQN+1=φ0+φ1PUQN-1+φ2PUQN-2+…+φPPUQN-P+et

(3)

其中φ0是常数项，φ1,φ2,φP是参数模型，这些参数可以从PUQ中计算，et均值为0，方差为σ的白噪声。

4.3 滑动平均(MA)

滑动平均法是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。本文中，可以将预测值表示为有限个历史随机白噪声的线性组合为式(4)。

PUQN=αN-θ1αN-1-θ2αN-2-…-θqαN-q

(4)

因此在本文中ARIMA模型整合了上述三个过程，最后热点i时间t处的预测值为式(5)。

PUQN+1=φ0+φ1PUQN-1+φ2PUQN-2+…+φPPUQN-P+et+αN-θ1αN-1-θ2αN-2-…-θqαN-q

(5)

由于一个热点中上/下车的PUQ值是一个自然数，但预测值可能是小数，而且这里的预测值是偏移之后的时间序列得来的，所以最后的预测值为PUQN加上之前的均值E之后得到。

5 PageRank与ARIMA预测值的关系

如上所述，Pi(t)和PUQN都可以表示地区的出租车需求状态。为了更直观的了解两者的关系，显示了中国人民大学附近两者一天内的变化情况如图4所示。

图4 中国人民大学附近一天Pi(t)和PUQN的变化

可以看出，高Pi(t)伴随着高PUQN，两者变化极为类似，基于这样的观察我们进一步探讨Pi(t)和PUQN的关系(PUQN量化为1到10)。

为了进一步确定Pi(t)和PUQN之间的相关程度，通过下面的等式计算Pi(t)和PUQN的Pearson相关系数(PCC)为式(6)。

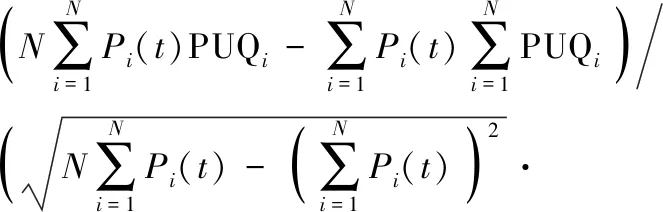
(6)

其中N是相应数据集中所有数据示例的数量。 列出了不同日期(假期，工作日和周末)和不同时间(早高峰时间，工作时间和晚高峰时间)的PCC如表1、表2所示。

表1 总时间段皮尔森系数

表2 一天中的皮尔森系数

从表1，表2可以看出，一天中Pi(t)和PUQN之间的平均Pearson相关系数为0.845 2。 除了周末的PCC小于0.8之外，其他情况下的PCC都大于0.8，这意味着Pi(t)和PUQN之间存在强的正线性相关性。因此，使用如下线性模型来拟合数据为式(7)。

PUQi(t)=a×Pi(t)+b

(7)

然后，使用最小二乘法进行拟合，拟合曲线显示如图5所示。

图5 拟合点分布图

可以看出其中大多数分布在对角线附近。

6 总结

以上研究意味着可以直接利用(7)来快速的做。为了进一步验证这一点，我们用(7)将Pi(t)作为输入，来对上下车乘客进行预测，预测的准确性被定义为式(8)。

(8)

表3 预测准确率

本文介绍了使用出租车GPS轨迹数据来预测某地出租车需求。提出了基于复杂网络中的PageRank流量建模，按照地区的上/下车乘客数量来划分热点，用ARIMA对热点区域乘客量预测，通过实验验证，发现大部分地区的PageRank值与ARIMA预测值的皮尔森系数平均为0.817 4，两者存在强正线性关系，并且对此进行了准确性验证，平均准确率为0.8446。因此PageRank值可以作为接下来热点出租车需求的一项指标。以上结果表明，以热点区域作为节点PageRank建模是一种更为合理的交通预测手段。

事实上，出租车轨迹数据的分析不仅对出租车需求预测有帮助，对交通警察管理城市交通，提高效率，人力资源的分配有很大作用[13]。另外还可以引导乘客在更短的时间内找到出租车，节省时间资源。还有对于司机，甚至城市规划也很有帮助[14][15]。具体可以分为以下3个方面：

6.1 对乘客的服务

(1) 交通费用预测

出租车计价是行驶距离和等待时间的函数，但根据路况的不同，如红绿灯的等待时间，以及紧急情况等会产生不同的费用。通过分析出租车在两地之间的频繁路线，综合道路具体情况来预测交通费用。

(2) 交通时间分析

交通时间通常包括人们等到交通工具的时间。可以使用两地的平均通行时间，也可以根据通行速度来进行推断。但是根据出租车计算时间有一定的局限性，出租车的等候时间灵活多变难以计算，等候的人群会因天气，时间太长节假日等情况产生影响。

(3) 候车信息推荐

为解决难打车问题，向乘客推荐合适的乘车地点以及准确的候车时间。

6.2 司机如何提高运行效率

(1) 道路路况检测

通过整体的出租车轨迹数据，实时监测路况，判断道路通畅，交通堵塞以及交通速度等情况进而分析最佳行车路线，最佳行车路线结合路况和学习出租车司机的只会，获得更好的行车路线。

(2) 载客策略

帮助司机更快更好的找到乘客，提高收益，减低油耗。

6.3 政府如何改善交通

(1) 路网规划

通过车辆轨迹，研究构建城市道路，走向。复杂的单双通行道路，高架等。但是存在一定的问题，出则车轨迹能否正确反应交通情况，以及出租车行驶路线并不一定是两地的最短距离。

(2) 交通供求分析

分析区域的交通客流量，建立公共交通体系，合理分配公共交通资源。

智慧城市作为一项新兴的全球技术，旨在对资源进行智能管理来促进可持续发展，将给人们带来高质量的生活！