一种基于倒排索引的频繁项集挖掘方法

（长春理工大学 计算机科学技术学院，长春 130022）

大数据时代的到来，数据呈爆炸式增长，为了能够从大量的数据中挖掘出有价值的信息，研究关联规则得到了高度的重视，关联规则挖掘过程一般包括两步：（1）频繁项集的识别（2）从频繁项集中挖掘隐含关联规则［1］。其中频繁项集的识别是整个挖掘过程的主要部分，频繁项集的规模也决定了数据挖掘性能。

目前，已有众多学者针对频繁项集挖掘的经典算法进行改进，他们分别从“事物：项集合”和“项目：事务集合”两种方式展开研究，前者被称为“水平数据格式”，后者被称为“垂直数据格式”。文献［2］利用了二维数组的结构来对算法进行了改进，大大减少了输入输出操作，使查找速度得到提高，但随着数据库中数据量不断增大，导致了数据库中的事务无法全部存入数组当中。文献［3］提出的十字链表和二维数组相结合的方法实现了频繁项集挖掘，但由于十字链表是静态的，不能随着挖掘过程的进行而随时压缩链表，因此增大了内存开销。针对上述算法的问题，在二维数组的基础上引入倒排索引结构，提出了一种基于倒排索引和二维数组的频繁项集挖掘算法。

1 基于倒排索引和二维数组的频繁项集挖掘

1.1 倒排索引表示事务数据库

倒排索引［4-5］（Inverted Index），也称为反向索引，是一种直接通过属性值来确定该属性所在记录位置的索引方法，包括词项词典和倒排记录表两个部分。倒排索引是信息检索系统中最常用的数据结构，倒排索引表是由一组包含属性值和属性所在地址的记录所形成的二维表，其存储结构对检索的效率和效果起着至关重要的作用。倒排索引结构如图1所示。

图1 倒排索引结构

为了提高频繁项集的挖掘效率，引入倒排索引技术，获取其对应的事务编号Tid，并按Tid对应事务的项目长度进行分组，构建倒排索引。其中倒排索引由两部分组成：第一部分是频繁项目，其内容是频繁项目头节点；第二部分是倒排索引节点，由项目长度和事务Tid列表组成，对Tid按照事务长度列表进行分块保存。对于包含N个项目的候选项集，采用倒排索引技术，每个候选项集只需扫描长度为N的头节点表，并取出头节点表中事务集合，这将大大提升扫描数据库效率，从而提高频繁项集挖掘的效率。

假设事务数据库D共有6条事务，事务中的项目用I1，I2，I3，I4，I5，I6表示，每条事务都按字典顺序排序，如表1所示。事务数据库D对应的倒排索引如图2所示，通过将项目的倒排索引转换为列向量，并用“与”运算得到支持度，最后删除小于支持度的频繁项集。

表1 原始事务数据库D

图2 事务数据库D对应的倒排索引

1.2 基于二维数组的候选k项集生成方法

首先，定义频繁项集Lk，候选项集CK。将（k-1）项频繁项集分为两部分存储到二维数组，记二维数组为Ak。将频繁（k-1）项集的前（k-2）项集存储到Ak的第0列，第（k-1）项集存储到Ak的第1列，分组编号存储到Ak的第2列，有效标识位存储到Ak的第3列，其中1表示该项集可以和其他项集链接，0表示不可以链接。例如，频繁3项集L3={{I1，I4，I6}，{I2，I3，I4}，{I4，I5，I6}}，它在二维数组Ak中的存储形式如表2所示。

表2 频繁3项集L3的二维数组

在存入二维数组Ak的过程中把频繁（k-1）项集分组，由于Apriori算法［6］在执行连接生成频繁K项集Lk+1的过程中，需要从Lk中找到两个项集与前k-1项集均相同的项集，才可以连接，因此分组规则是把与第0列相同的频繁项集分成一组；根据表2可知，频繁3项集L3应该分成三组，第0行的{I1，I4，I6}分在第1组，第1行的{I2，I3，I4}分在第2组，第2行的{I4，I5，I6}分在第3组。由于两个频繁（k-1）项集链接生成候选项集Ck时，必须满足前k-2项相同，第k-1项不同。根据链接条件，三组项集均无法与其他项集进行链接，所以第3列的有效标识位均为0。在生成候选k项集Ck时按照分组来进行，因为分组后的频繁项集正好满足了链接条件，不仅能生成所有的候选k项集，而且不会产生多余的候选k项集。

2 实例分析

下面以部分实验数据为例说明挖掘频繁项集的过程：

扫描数据库，生成倒排索引。在生成倒排索引前首先根据项目编号得到对应的Tid值，再按照每个项目的Tid值个数进行分组，最后生成每个项目和Tid值的倒排索引。如图2所示。

再次扫描数据库，获得频繁1项集L1={I1，I2，I3，I4，I5，I6}，然后将频繁1项集存入二维数组中，当存入二维数组时，需要遵循一定的规则，其中二维数组有四列，每列数据都有不同的意义，以频繁1项集为例，第0列存储前k-1项频繁项集，因为频繁1项集不存在前k-1项频繁项集，所以第0列用空表示，第1列存储第k项集，第2列存储在第0列基础上的分组编号，第3列代表各项集间是否可以链接，可以链接记为1，否则记为0。所以频繁1项集对应存储的二维数组如表3所示。

表3 频繁1项集的二维数组

接下来生成频繁2项集，由于所有频繁1项集的第0列相同，且标志位均为1，因此直接链接生成候选频繁 2 项集 C2={I1I2，I1I3，I1I4，I1I5，I1I6，I2I3，I2I4，I2I5，I2I6，I3I4，I3I5，I3I6，I4I5，I4I6，I5I6}，再通过上述的倒排索引技术计算支持度来筛选频繁2项集。支持度计算以I1I4为例，I1的倒排索引是（1，6），相应的列向量R1=（1，0，0，0，0，1）T，I4的倒排索引是（1，3，4，5，6），相应的列向量R2=（1，0，1，1，1，1）T，计算R1&R2=（1，0，0，0，0，1）T，R1&R2结果中1的个数就是支持度，综上所述可知I1I4的支持度是2，假设实验设定最小支持度为2，因为I1I4的支持度等于2，所以I1I4为频繁项集，依次计算得到频繁2项集L2={I1I4，I1I6，I2I3，I2I4，I3I4，I4I5，I4I6，I5I6}。

利用上述方法生成频繁3项集L3={{I1I4I6}，{I2I3I4}，{I4I5I6}}。

接下来计算频繁4项集，根据性质，频繁k项集若能产生频繁（k+1）项集，那么频繁k项集中项集个数肯定大于k。由于L3的个数小于4，因此不能生成频繁4项集，算法结束。

3 实验结果及分析

为了验证算法的性能，分别在以下两方面与文献［2］、文献［3］中的算法做了对比：一是最小支持度阈值不变，数据集规模不断增加的情况（如图3所示）；二是数据集大小一定，支持度不断增加的情况（如图4所示）分别得出实验结果。

根据图3所示，当最小支持度阈值不变而数据集不断增加时，在数据集未达到25万时，算法ALN的运行时间较短；当数据集超过25万之后，文中算法的运行时间明显少于Apriori-BR和ALN两种算法，更适用于大数据的频繁项集挖掘。

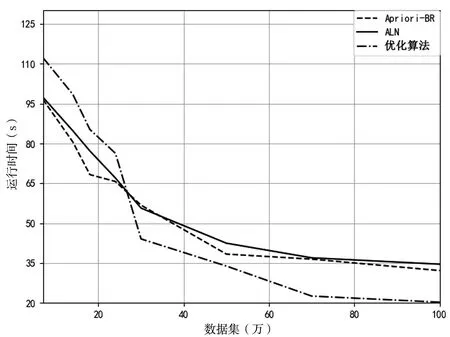
图3 不同数据集下的运行时间结果

图4 不同最小支持度下的运行时间结果

根据图4所示，在原始数据集不变，最小支持度阈值改变时，文中提出的算法比Apriori-BR和ALN生成频繁项集的系统运行时间短，故比其他两种算法更高效。

4 结束语

通过对文献［2］和文献［3］算法的改进与结合，提出基于倒排索引和二维数组的频繁项集挖掘算法。虽然该算法需要扫描两次数据库，但在数据集较大的时候，倒排索引技术大大提高了检索效率，运行时间也相对较少。在计算支持度时无需扫描数据库，并且通过标志位约束减少候选项集的生成数量，从而提高了候选项集的连接效率以及内存利用率。