容重对红壤区地下滴灌水分入渗能力影响研究
贾洪涛, 张鹏飞, 代智光
(1. 黄河水利职业技术学院,河南 开封 475000;2. 南昌工程学院,江西 南昌 330099)
红壤是我国南方分布最广的地带性土壤之一,合理和科学利用红壤资源,对我国农业的可持续发展具有重要意义[1]。目前,我国红壤地区仍以地面灌为主,不仅水分利用效率低下,而且加剧了当地水土流失的风险,因此,要保证红壤地区农业的可持续发展,必须发展节水灌溉。地下滴灌(Subsurface Drip Irrigation,简称SDI)是在滴灌基础上发展而来的一种高效节水技术,它通过地埋式滴灌带上的滴头将水或肥液直接输送到作物根区,实现了地下局部灌溉。与其他灌水技术相比,地下滴灌可以有效降低地表蒸发和深层渗漏,且在一定程度上能抑制杂草生长,同时由于滴灌管埋于地下,无需占用耕地,提高了土地的使用率,具有广阔的应用前景[2,3]。
土壤水分入渗主要受土壤容重、土壤机械组成以及土壤初始含水量等因素的影响,而土壤容重的影响尤为显著[4-6]。土壤容重作为土壤的一个基本物理指标,对土壤的透气性、入渗特性、溶质迁移特性以及抗侵蚀能力都有很大的影响[7-9]。相关学者关于土壤容重对水分入渗能力影响进行了大量研究,裴青宝和曾健等[10,11]分别研究了地表滴灌条件下容重对红壤水分入渗的影响,结果表明,容重对土壤水分水平和垂直入渗特性均有显著影响;李卓等[12]通过人工配制不同典型土壤,研究了容重对积水入渗土壤水分入渗能力的影响,结果表明土壤初始入渗能力随容重的增大而递减,而入渗能力的衰减速度随容重增大而递增;刘小刚等[13]研究了不同容重条件下微润灌溉湿润体内水分的分布特性,结果表明,容重对微润灌溉土壤湿润体内含水率的影响达到显著水平。
目前关于红壤水分入渗能力的研究报道还很少,仅是针对地表滴灌水分入渗开展了初步研究,而关于容重对红壤条件下地下滴灌水分入渗能力影响的研究还未见报道。基于此,以具有典型的江西红壤为例,通过室内入渗试验,研究容重对土壤水分入渗能力的影响,确定容重与水分入渗能力的定量关系,以期为地下滴灌技术在红壤地区的推广应用提供理论参考。
1 材料与方法
1.1 试验土壤
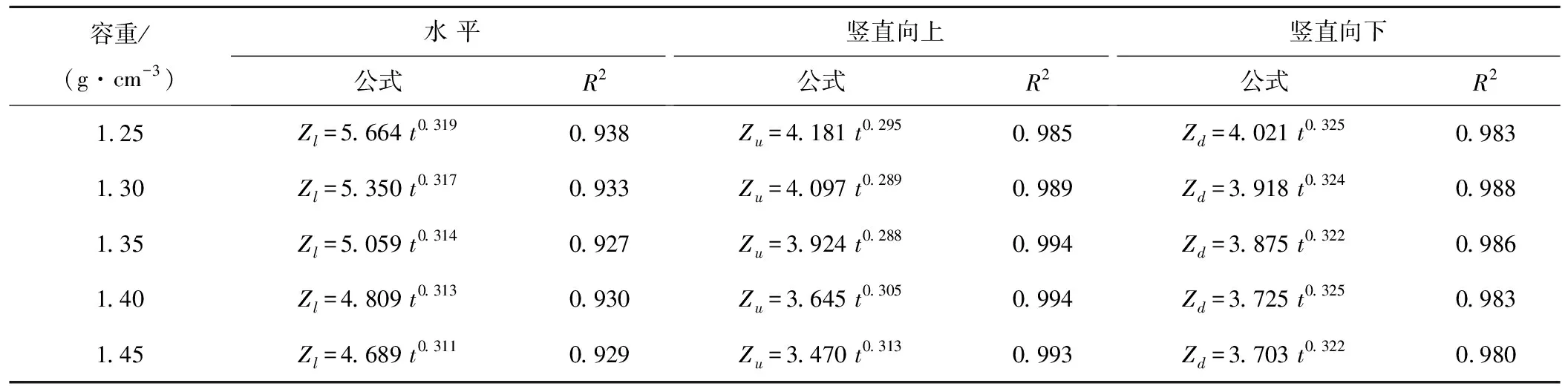
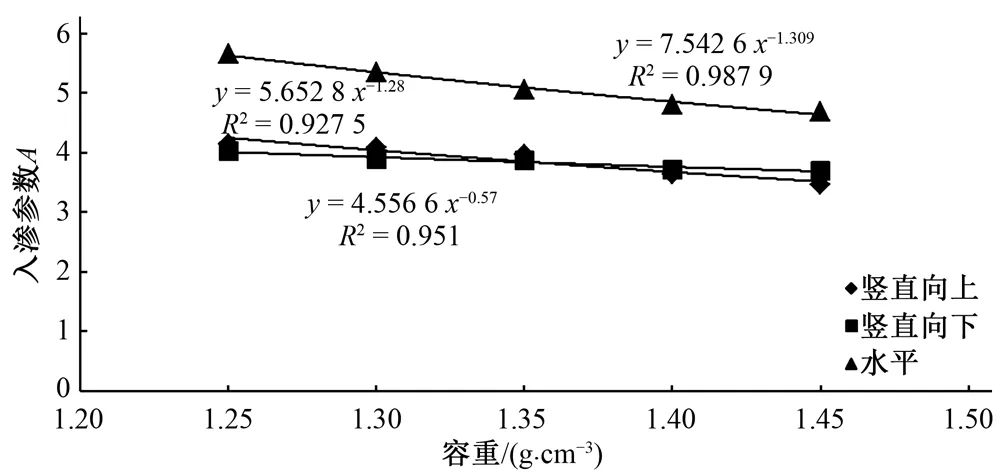
试验于2018年3-4月在南昌工程学院灌溉排水实验室进行,供试土壤取自江西省进贤县田间表层0~50 cm深度,土壤经自然风干后过2 mm筛。土壤颗粒组成用激光粒度分析仪(MS2000型)测定,粒径为0 mm 试验装置由马氏瓶、土箱、输水管和微管组成(图1)。马氏瓶用于提供恒定水头,其内径为14 cm,高为100 cm,通过调整出口开关来控制出流流量;土箱材质为有机玻璃,尺寸为50 cm×50 cm×100 cm(长×宽×高),并在土箱上口边角向下20 cm处开一直径为3.10 mm的圆孔;输水管为一内径为3 mm的乳胶管;微管外径为3 mm,一端表面涂抹502胶水塞入土箱孔内并用纱布封口以避免土壤颗粒堵塞微管,模拟地下滴灌的滴头,另一端用橡皮筋与输水管连接。试验装置示意见图1。 图1 试验装置示意图 试验土壤初始含水量为7.60%,设定初始流量为1.50 L/h,灌水时间为240 min。土壤容重设置5个水平,分别为1.25、1.30、1.35、1.40、1.45 g/cm3。将试验土壤按容重分层(5 cm)装入土箱,层间打毛,自然沉降24 h后开始试验,按照先密后疏的原则观测马氏瓶读数,同时以滴头位置为起点,用直尺测量湿润锋在水平、竖直向上和竖直向下方向的运移距离,试验结束后,用塑料薄膜覆盖以防止水分蒸发。试验结束时、重分布1 d和3 d,在距离滴头水平距离5 cm处使用土钻取土,每隔10 cm取一次样,取土深度为100 cm,采用烘干法测定土壤含水率。每组试验重复3次,取其平均值进行分析。 图2为不同土壤容重条件下各向湿润锋的运移距离随时间的变化。在同一容重条件下,湿润锋均随着时间的推移而逐渐增大,但增大速度逐渐变慢,且湿润锋在各方向上的运移距离存在差别,在灌水结束时,水平方向湿润锋的运移距离最大,其次为竖直向下方向,而竖直向上方向湿润锋的运移距离最小。当入渗时间相同时,湿润锋运移距离在不同容重间存在显著差异,随着土壤容重的逐渐增大,湿润锋的运移距离均表现出逐渐减小的趋势,在水平方向,容重为1.25 g/cm3时,湿润锋运移距离为28.7 cm,而容重为1.45 g/cm3时,湿润锋运移距离仅为22.6 cm,下降了22.60%;在竖直向下方向,容重为1.25 g/cm3时,湿润锋运移距离最大,为26.2 cm,与其他容重相比,分别增大了2.34%、4.38%、9.17%和11.49%;在竖直向上方向,当容重为1.25和1.30 g/cm3时,湿润锋到达了土箱表面,而容重为1.35、1.40和1.45 g/cm3时,湿润锋至土箱表面的距离分别为0.7、1.0和1.2 cm。这是由于土壤容重较小时,土壤内部大孔隙较多,土壤连通性好,土壤的导水率也较高,因此土壤水分的运移距离也较大,而随着土壤容重的增大,土壤内部大孔隙的数量急剧减小,土壤内部连通性变差,且封闭气体进一步阻碍了土壤水分的运动,因此湿润锋运移距离也逐渐减小。 经分析,在地下滴灌条件下,各向湿润锋的运移距离与入渗历时均符合幂函数的关系,即: Z=Atb (1) 图2 剖面各向湿润锋运移距离随时间变化 式中:Z为湿润锋运移距离,cm;t为入渗历时,min;A、b为入渗参数。 拟合结果表明,湿润锋在水平、竖直向上和竖直向下方向的运移距离与入渗历时拟合公式的决定系数均大于了0.927,且大于其临界决定系数(R0.01=0.605 5)(表1),这说明拟合公式的精度满足要求,即在地下滴灌条件下,各向湿润锋的运移距离与入渗历时均呈幂函数正相关的关系。由表1可知,随着土壤容重的增大,入渗参数A表现出逐渐减小的趋势,而入渗参数b的差别不大。 表1 剖面湿润锋运移距离拟合 注:Zl、Zu、Zd分别为湿润锋在水平、竖直向上和竖直向下方向的运移距离,cm;t为入渗历时,min。 为进一步分析土壤容重对湿润锋运移的影响,对入渗参数A和土壤容重γ的关系进行拟合。由图3可知,湿润锋入渗参数A与土壤容重γ符合幂函数负相关的关系(R0.01=0.958 7),且在水平方向,湿润锋入渗参数A始终最大。 图3 各向湿润锋入渗参数A与土壤容重关系 由图4可知,在相同容重条件下,通过对累计入渗量与入渗历时的拟合结果表明,累计入渗量与入渗历时均呈线性正相关关系,其决定系数均在0.99以上,当容重分别为1.25、1.30、1.35、1.40和1.45 g/cm3时,对应拟合线的斜率分别为0.022 6、0.021 4、0.020 8、0.020 4和0.020 2,这说明随着容重的增大,土壤入渗量的增长幅度逐渐减小。在试验结束时,当容重为1.25 g/cm3对应累计入渗量最大,为5.46 L,1.30、1.35、1.40和1.45 g/cm3处理与之相比,分别下降了3.91%、7.73%、8.98%和10.39%。对于同一容重而言,随着时间的推移,入渗率在开始阶段迅速下降,最后逐渐趋于稳定入渗率;土壤入渗率在不同容重间的差异显著,其中容重为1.25 g/cm3时,土壤水分入渗率始终最大,且在140 min时土壤水分入渗才达到稳定,稳渗率为0.023 6 cm/min,而容重为1.45 g/cm3时,在入渗30 min时,土壤水分入渗就基本稳定,稳渗率仅为0.018 7 cm/min,相比最大值,下降幅度达26.20%。 图4 不同容重土壤累计入渗量及入渗率随时间变化 为进一步分析累计入渗量和稳渗率与容重的关系,本文对土壤累计入渗量以及稳渗率与土壤容重关系进行了拟合(图5)。结果表明,累计入渗量及稳渗率与土壤容重均符合幂函数负相关的关系(R0.01=0.958 7),这说明,当土壤容重较小时,累计入渗量及稳渗率受容重的影响很大,但随着容重的增大,容重对累计入渗量及稳渗率的影响逐渐变小。 图5 土壤累计入渗量及稳定入渗率与土壤容重关系 图6 不同土壤容重下各土层含水量分布 在生产实践中,一般认为灌水后2~3 d后土壤水分基本趋于稳定,因此,有必要对土壤水分重分布的过程进行研究。图6表明,在灌水结束以及重分布1 d和3 d,不同容重对应土壤含水率在土层中的分布基本一致。对于同一容重而言,在灌水结束时,土壤含水率在0~100 cm深度范围内差别较大,其中20 cm土层对应土壤含水率均最高,容重为1.25、1.30、1.35、1.40和1.45 g/cm3对应最高含水量分别为43.5%、41.8%、40.5%、39.4%和38.7%。随着时间的延长,土壤含水率在土层内分布逐渐均匀,重分布1 d时,在重力势的作用下,土壤水分之间下渗,其中容重为1.25、1.30和1.35 g/cm3对应土壤水分均逐渐降至70 cm深度以下,此时,土壤水分最大值仍出现在20 cm深度,但其值有所下降,容重为1.25、1.30、1.35、1.40和1.45 g/cm3对应土壤含水率分别为36.4%、34.6%、33.7%、32.8%和32.1%,相比灌水结束时,分别下降了19.51%、20.81%、20.18%、20.12%和20.56%。在重分布3 d时,所有容重对应土壤水分均下降至80 cm以下,此时,土层含水率的最大值也出现在30 cm深度,容重为1.25、1.30、1.35、1.40和1.45 g/cm3对应土壤含水率分别为27.8%、26.8%、26.2%、25.2%和24.7%。这是由于水分向土壤深层运动造成的。对于同一深度土层而言,灌水后不同时刻土壤含水率均随着土壤容重的增大而逐渐减小,这是由于随着土壤容重的增大,土壤中的空隙含量逐渐较小,因此土壤的持水能力也逐渐减弱。 基于土壤水分入渗的基本理论-达西定律,国内外学者相继提出了Kostiakov模型、Green-Ampt模型、Horton模型以及Philip模型等一系列模型,其中Kostiakov模型由于公式简单精确,在生产实践中得到了大量应用[14,15],其公式如下: f(k)=Kt-α+A (3) 式中:f(t)为入渗率,cm/min;t为累计入渗时间,min;A为稳定入渗率,cm/min;K和α为模型参数,其中K值与土壤初始入渗速率密切相关,其值越大,土壤初始入渗速率也越大,而α大小则反映了土壤入渗速率的衰减速率,α值越大,土壤水分入渗速率的衰减速度越快。 通过对土壤水分入渗率与时间的拟合结果来看,决定系数R2均在0.80以上,大于临界决定系数(R0.01=0.605 5),这说明用Kostiakov模型来模拟土壤水分的入渗过程是合理的。由表2可知,当土壤容重从1.25 g/cm3增大至1.45 g/cm3时,模型参数K值从0.554减小至0.348,而参数α则从0.435增大至0.661,这说明随着容重的增大,土壤水分初始入渗率逐渐减小,而其衰减速率则随着容重的增大逐渐加快。 表2 Kostiakov模型拟合 注:f(t)为入渗率,cm/min。 通过对模型参数K和α与容重的拟合结果来看,其决定系数均大于临界决定系数(R0.01=0.958 7),这说明模型参数K与土壤容重呈幂函数负相关的关系,而模型参数α与土壤容重则表现为对数正相关的关系(图7)。随着容重的增大,土壤中大孔隙的数量急剧减小,因此土壤的初始入渗能力也逐渐降低,且随着容重的增大,土壤内部气体排出逐渐困难,且土壤的连通性逐渐变差,导致土壤的导水能力急剧下降,因此入渗率也迅速衰减,此时在模型上也就表现出随着容重的增大,模型参数K值逐渐减小,而参数α值则逐渐增大。 图7 土壤容重与Kostiakov入渗模型参数关系 (1)红壤区容重对土壤入渗能力有显著影响,容重越大,土壤湿润锋运移距离、累计入渗量以及入渗率均越小,各向湿润锋的运移距离与入渗历时呈幂函数正相关的关系,而累计入渗量和稳渗率与容重均呈幂函数负相关的关系。 (2)在不同容重条件下,土壤含水率的剖面分布基本一致,其中灌水结束时和重分布1d时,20cm深度对应土壤含水率最大,而在重分布3d时,30cm深度对应土壤含水率最大,且在同一深度范围内,随着容重的逐渐增大,灌水后不同时刻含水率均逐渐减小。 (3)红壤区地下滴灌土壤水分入渗过程符合Kostiakov模型,模型参数K与容重呈幂函数负相关的关系,而模型参数α与土壤容重呈对数正相关的关系,这说明土壤初始阶段的入渗率随着容重的增大而降低,而入渗率的衰减速度随着容重的增大而逐渐加快。1.2 试验装置
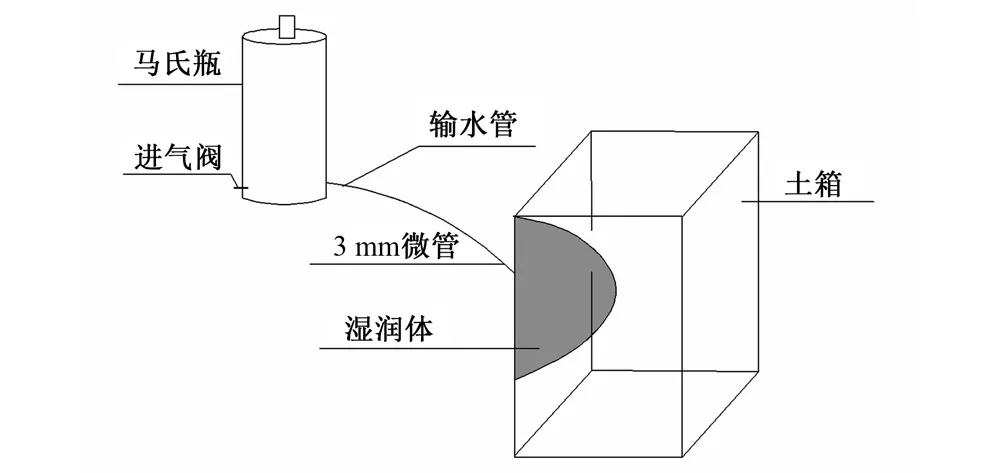
1.3 试验设计与观测内容
2 结果与分析
2.1 土壤容重对剖面湿润锋运移特性的影响
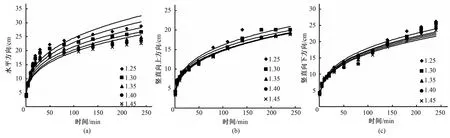
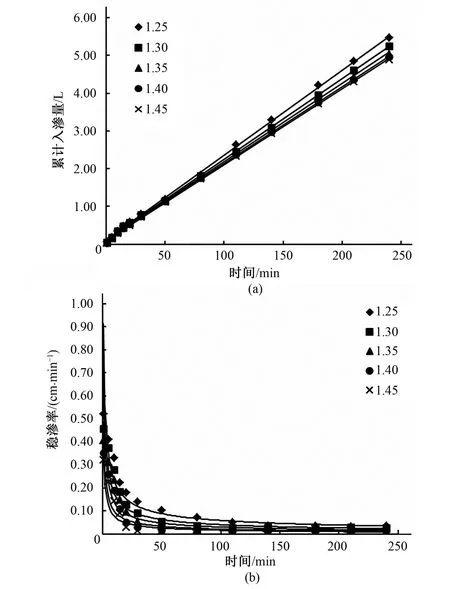
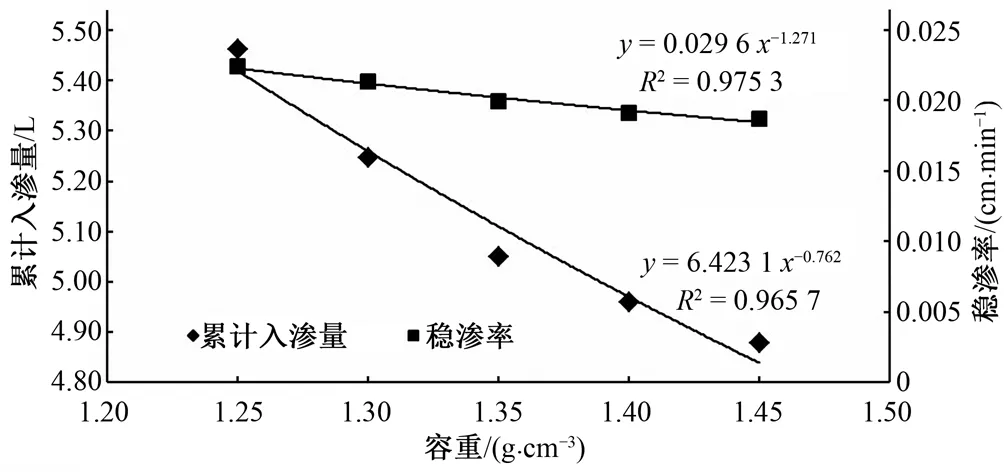
2.2 土壤容重对累计入渗量及入渗率的影响

2.3 容重对土壤剖面含水率分布的影响
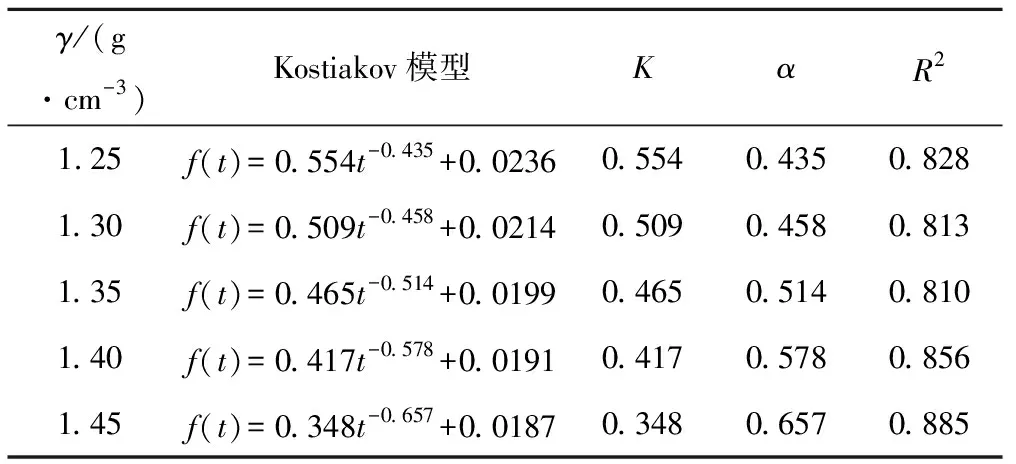
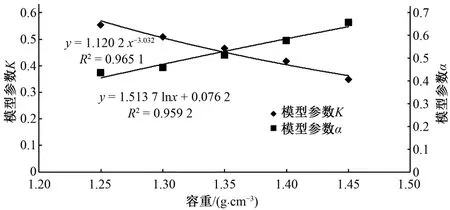
2.4 土壤容重对入渗模型参数的影响
3 结 论

