扬州城区古运河局部河段水质时间变化特性----以扬农化工厂河段为例

周亚明，黄涌增，黄金柏，周 钦，甄自强

(扬州大学水利与能源动力工程学院，江苏 扬州 225127)

0 前 言

城市河网由流经城市和城市范围内的河道连接而成，是城市生态环境的重要组成部分[1]，为城市提供多种社会和生态服务：如生产、生活用水，防洪排涝，排污纳污，景观文化以及气候调节等。但是随着城市化的发展，河网水系结构趋于单一化和主干化[2]，水循环过程受阻，自净能力降低，许多城市出现比较严重的水污染问题。城市河流水环境恶化对城市发展、城市居民健康和生态环境构成严重威胁[3]。许多学者针对城市河流的水质问题开展研究，欧美国家在这方面的研究起步较早，实例较多。如Berkant等[4]利用河流的水文网络资料，分析土耳其河流的水质水量时空变化趋势，对河流水质水量的控制提供评估；Bahman等[5]对河流的pH、溶解氧、悬浮固体等参数进行调查，并研究流域土地覆盖的构成与河流水质属性之间的关系；Ishaq等[6]对尼日利亚Benue河10个不同地点的水质参数时空变化进行调查，并利用判别函数对水质参数进行分析；Faridah等[7]利用水质指数(WQI)评估马来西亚巴生河流域的水质状况。近年，国内城市河流水质问题越来越受到重视，有关研究发展很快，如崔雪梅等[8]利用4种河流水质评价方法对槐荫河的水质进行评价，并比较4种评价方法的优缺点和实用性；程琳琳等[9]利用水质标识指数法分析河北省七大水系水质的时空变化特征，探讨了典型人类活动对水质的影响；嵇晓燕等[10]基于国家地表水环境质量监测网2006-2015年的数据，对淮河流域的化学需氧量和氨氮浓度变化特性进行了分析；王杰等[11]对昆明滇池的水质时空变化特性进行了分析。

古运河在扬州市的兴起和发展过程中发挥着重要的作用[12]。古运河连接扬州城区多条河道，是扬州城区河网排水的主要载体，也是重要的城市景观和航运通道，沿河分布着数十家工业企业单位，排污量较大，由于部分支流水质较差且代谢缓慢，导致古运河水质污染严重。为揭示古运河水质的变化特性，本文选取扬农化工厂河段为研究对象，对该河段的水质进行观测，对水质参数的时间变化特性进行分析，研究以期为古运河的水质与水生态研究提供基础数据，以及为河流水质监测和分析等研究提供方法上的借鉴。

1 材料和方法

1.1 研究区概况及水质观测

选取古运河流经扬农化工厂的河段为研究区。该化工厂存在时间较长、排污量大，对古运河局部河段的水质有较大的影响。研究河段存在两条支流，分别为安墩河和新城河。选取该河段上下游各一个断面(上游观测断面p1：32°22′58.69″ N，119°25′32.3″ E，到排水口的距离约1 000 m；下游观测断面p2：32°22′20.37″ N，119°25′0.42″ E，在靠近排水口的下游)，以及两条支流的入口断面(安墩河观测断面p3：32°22′46.66″ N，119°25′21.3″ E；新城河观测断面p4：32°22′24.79″ N，119°24′59.35″ E)(图1)开展水质观测活动。利用多参数水质分析仪(型号：YeoKal 615型多参数水质分析仪，产地：澳大利亚)对水温WT、pH、溶解氧DO、电导率EC和溶解性总固体TDS进行一周2次的观测，观测时段为2015年10月至2017年9月，为期2年。

图1 古运河流经化工厂河段及水质观测断面示意图

1.2 研究方法

1.2.1 相关系数法

相关系数法是常用的统计方法之一，主要用于分析两个具有物理成因联系的变量之间的相关性，其计算公式为[13]：

(1)

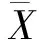
1.2.2 变异系数法

变异系数是样本的标准差与样本均值的比值，是反映样本分布离散程度的指标，变异系数越大，则样本分布离散程度越高。变异系数法基于指标数据推求各参数的权重，能够较为客观地反映评价指标的相对重要程度[14]。变异系数以及权重的计算公式为：

(2)

(3)

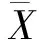
1.2.3 单因子水质标识指数法

徐祖信(2005)提出了单因子水质标识指数法[15]，该方法不仅可以根据各因子的水质标识指数计算结果直观判断水质的污染程度，并且可以对劣Ⅴ类水进行区分[16]，其计算公式为：

Pi=X1.X2X3

(4)

其中X1为第i项指标的水质类别，将测得的水质参数与《国家地面水环境质量标准》(GB3838-2002)进行比较，确定水质类别，水质类别为Ⅰ类，则X1为1，以此类推。

由于DO是重要的水质因子，也是衡量水体自净能力的主要指标之一[17]，因此选取DO作为单因子水质标识指数法的评价指标。以DO为评价指标时，X2计算公式为：

(5)

式子：ρDOk上为k类水质DO的上边界值；ρDOk下为k类水质DO的下边界值；ρDO为DO实测浓度。

当水质劣于Ⅴ类水时，计算公式为：

(6)

式中：m为计算修正系数，一般取4。

X3为水质类别与功能区规划设定类别的比较结果，为一位或两位有效数字。若水质类别好于或达到水环境功能区类别，则X3取0；若水质类别比功能区类别差且X2不为0，则：

X3=X1-fi

(7)

若水质类别比功能区类别差且X2等于0，则：

X3=X1-fi-1

(8)

式中：fi为水环境功能区类别。

1.2.4 多元线性回归法

多元线性回归法根据因变量和自变量的实测序列建立回归方程，对方程中的未知参数进行估计，利用所得多元线性回归模型预测因变量的变化趋势[18]。本研究采用多元线性回归法分析WT和pH对DO的影响，设DO实测值为y，回归值为Y，WT为X1，pH为X2，假定多元线性回归方程为Y=b0+b1X1+b2X2，其中b0，b1，b2为待定系数，将观测数据代入方程(矩阵形式)Y=XB，其中：

计算中间变量：

(9)

(10)

(11)

(12)

(13)

建立矩阵方程：

(14)

解出b1，b2值，并根据公式 推求b0的值，得到多元线性回归模型。

采用R检验法检验DO与WT、pH的线性关系，其公式为：

(15)

若R≥0.8，说明DO与WT、pH之间相关性显著，则该模型可以较好反映三者的线性关系。

2 结果与分析

2.1 观测结果

图2所示为观测期间上下游断面(p1，p2)的WT和DO的变化过程，由该图可知，WT变化的周期性十分明显，自1月中旬至7月末WT逐渐升高，最高约为33 ℃；自8月初至次年1月中旬WT逐渐降低，最低为3 ℃左右；当WT增大时，DO呈下降趋势，说明溶解氧的浓度与水温呈反比。观测期间内，p1断面的DO多高于p2，说明工厂排污对p2断面DO有较大影响，DO偏低。

图3为p1，p2的pH和DO变化过程，由该图可知，在研究期间内，除2016年10-12月和2017年7-9月pH呈上升趋势，其余时段pH均呈下降趋势。对各时段观测结果的分析可知，一般情况下，DO随pH升高而增大，随pH下降而减小，DO与pH变化过程相似。

图2 p1, p2断面的WT与DO变化曲线

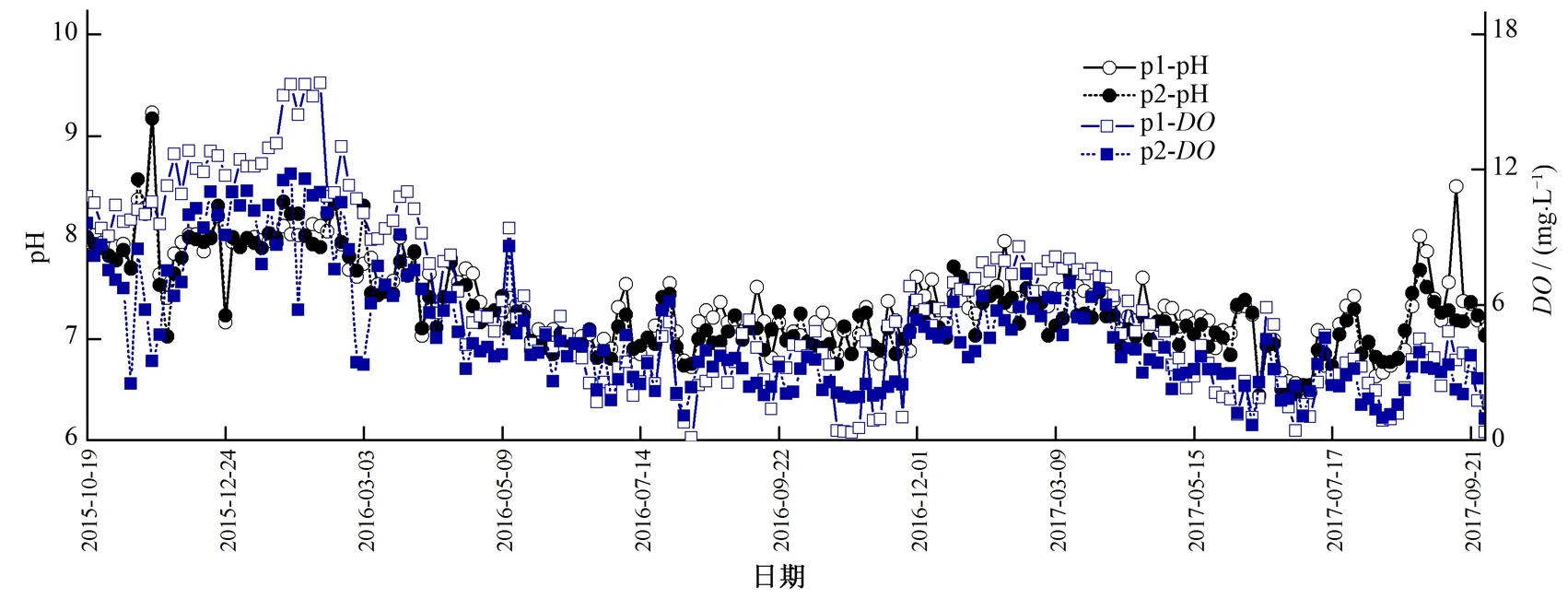
图3 p1, p2断面的pH与DO变化曲线

由图4可知，同一断面EC与TDS变化曲线的形状几乎一致，因为两者都与水中溶解离子的总浓度有关，是反映水中溶解杂质含量的参数，具有较强的物理成因联系。EC和TDS除2016年4-10月有所降低，其余时段变化不大；大部分情况下同一时间p2断面的EC和TDS均高于p1，说明p2断面受化工厂排污影响，水中杂质和离子浓度均高于p1。

图4 p1,p2断面的EC与TDS变化曲线

图5、6和7分别为安墩河与兴城河流入古运河断面(p3，p4)WT和DO、pH和DO、EC和TDS的变化过程，由图5-7可知，在对应的时间点上，p3各水质参数的观测结果多高于p4，其中p3的EC和TDS在选取的4个观测断面中最高。根据调查，p3断面有水闸控制，闸门平时关闭，在此期间，安敦河与古运河研究河段水体无交换。研究期间水闸开启频率约为一个月一次，且两支流流量较小，对研究河段水质观测结果影响不大，因此本研究未对两支流(安敦河与兴城河)汇入古运河断面(p3、p4)的水质进行评价。

图5 p3,p4断面WT与DO变化曲线

图6 p3,p4断面pH与DO变化曲线

2.2 相关性分析

以季度为时段，对观测周期进行划分，各季度p1，p2断面同一水质参数的相关系数计算结果如表1所示。

由表1可知，各季度WT的相关系数均大于0.9，总相关系数为0.994，接近完全相关；pH与DO相关系数呈现出相似的季节性变化趋势，当pH相关系数增大时，DO相关系数也增大，且两者都于2017年1-3月降至最低；同一季度EC和TDS的相关系数近似相等，多个季度p1，p2的EC和TDS序列均呈显著相关或高度相关。在观测周期内，p1，p2各水质参数总相关系数均大于0.8，均呈高度正相关，但个别时段的pH、DO、EC以及TDS的相关系数不高，正相关性不显著，如2017年1-3月，p1和p2的pH与DO的相关系数仅为0.301和0.194；2017年4-6月两断面EC和TDS的相关系数分别为0.491和0.495，为观测期间较低水平。导致相关系数时段性降低的原因是p2断面水质受化工厂排污的直接影响，而p1断面未受影响，造成两断面参数时段性变化的差异较大，因此相关系数偏低。

图7 p3,p4断面EC与TDS变化曲线

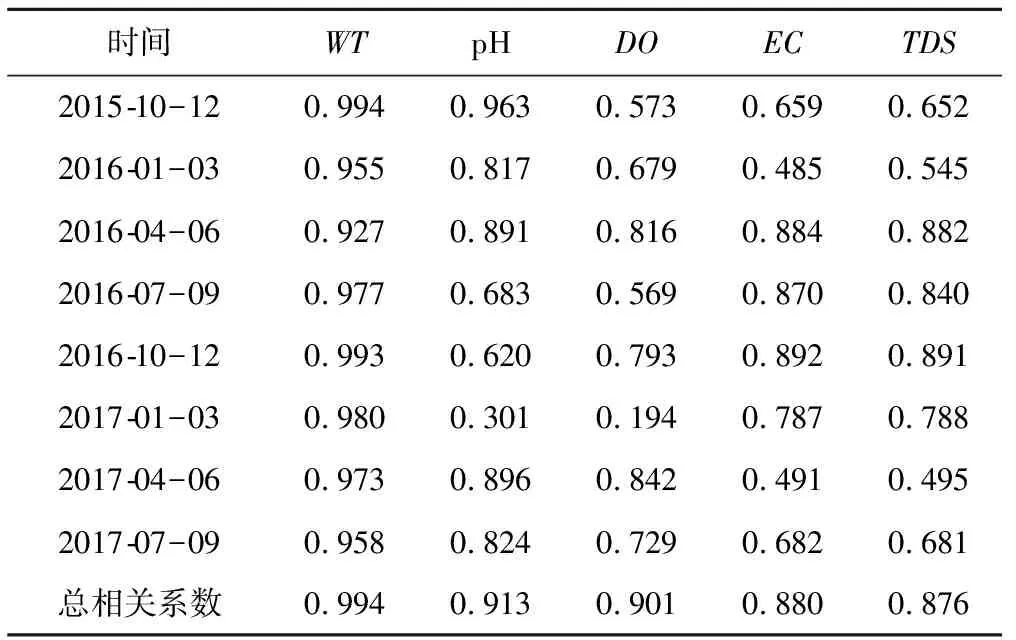
表1 p1,p2断面各水质参数不同季度的相关系数计算结果

2.3 变异性分析

p1，p2各水质参数以季度为时段变异系数的计算结果如表2所示。

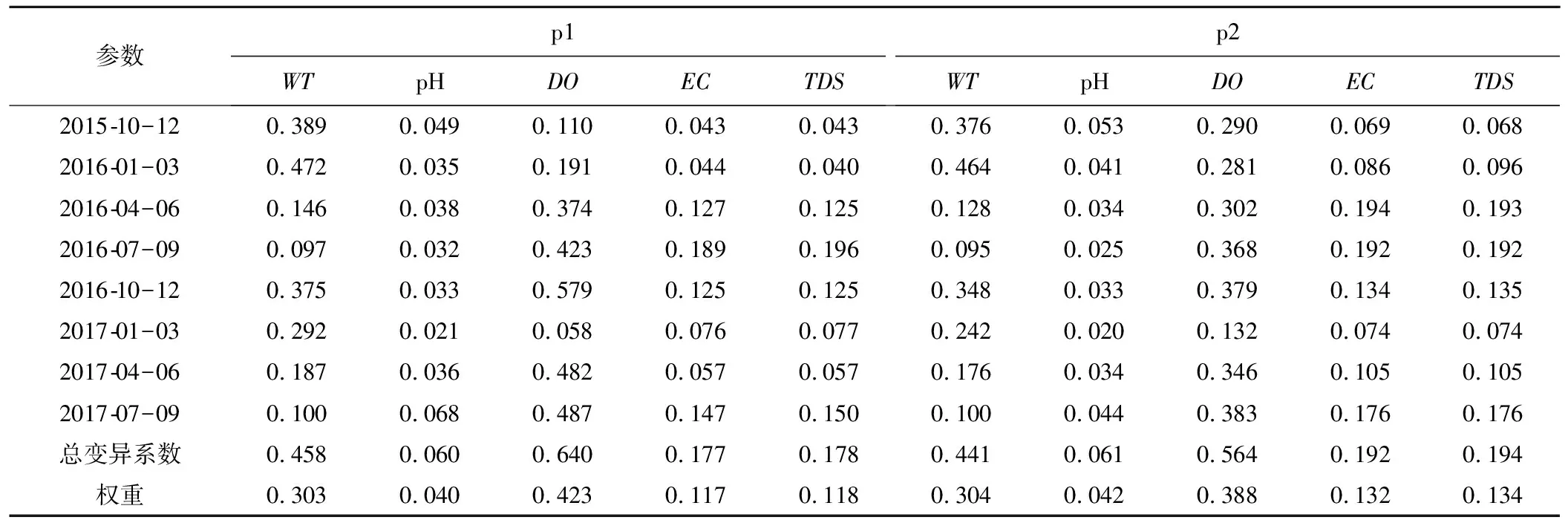
表2 p1,p2各水质参数不同季度的变异系数计算结果

从表2可以看出，p1断面WT的变异系数略大于p2，2016年一、四季度的变异系数明显高于其他时段，说明春冬两季WT的波动程度较高；各季度pH的变异系数均小于0.1，说明pH变化缓慢，波动较小，比较稳定；DO变异系数的季节性变化较大，两断面DO变异系数变化范围在0.05～0.60之间，整体上，气温较低时段的DO变异系数小于气温较高的季节，由此也证实了溶解氧的浓度与WT成反比。气温低有利于氧气的溶解，而水中化学反应和生物代谢较慢，消耗的氧气减少，因此DO的波动性降低；多数季度p2断面EC和TDS的变异系数均大于p1，说明化工厂排污使p2的EC和TDS波动程度增大；权重计算结果表明，各水质参数的权重从高到低依次为DO>WT>TDS>EC>pH(表2)。

2.4 单因子水质标识指数法分析结果

利用单因子水质标识指数法计算p1，p2断面DO的单因子标识指数，由于DO受WT和pH影响较大，分别作水质标识指数与WT、pH的变化曲线，结果如图8、9所示。

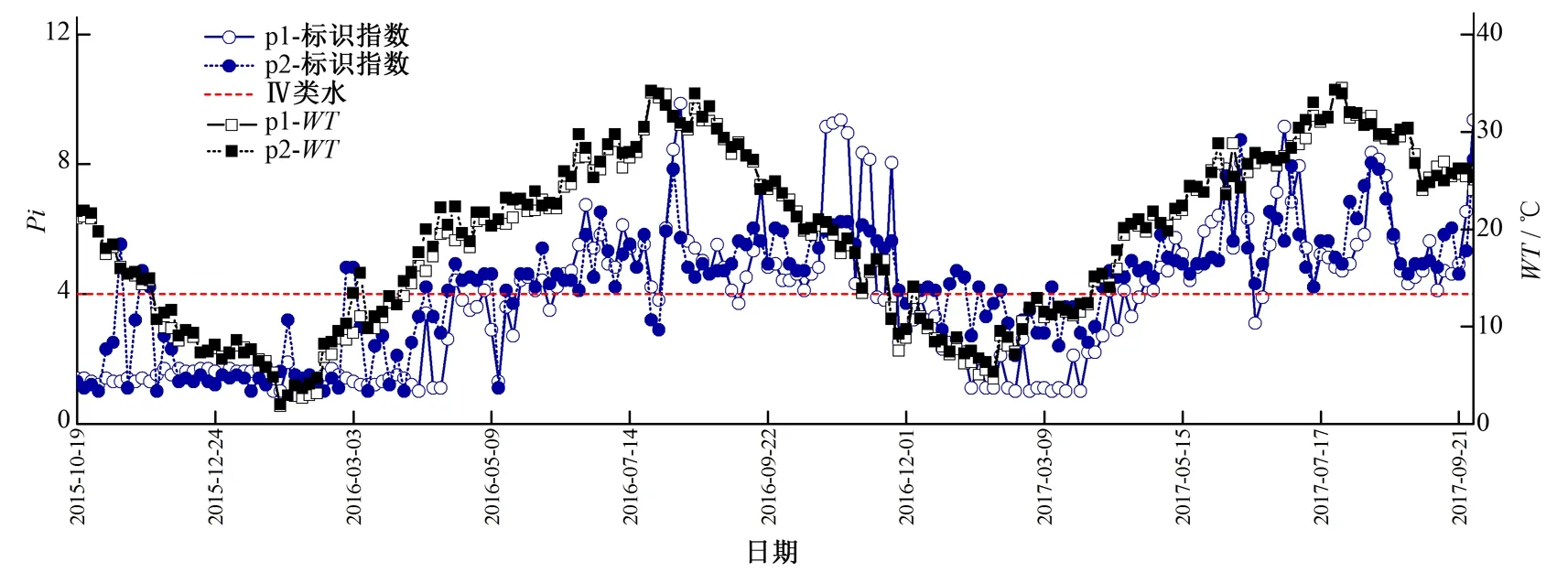
图8 p1,p2断面DO单因子水质标识指数与WT变化曲线

图9 p1, p2断面DO单因子水质标识指数与pH变化曲线

扬州市古运河水功能区水质目标为Ⅲ类。由图8、9可知，自2015年10月至2016年4月，p1，p2的水质基本满足扬州市古运河水功能区目标(Ⅲ类)；2016年5月至11月，p1，p2断面水质多为Ⅳ、Ⅴ类水，部分时段的DO水质标识指数大于6，劣于Ⅴ类水；2016年12月至2017年3月水质标识指数降至4以下，满足水功能区水质目标；之后水质标识指数又升至4以上。在观测时段的大部分时间，p1断面水质优于p2。

从整体上看，DO水质标识指数随WT的升高而增大，随pH升高而减小(图8、9)。当WT低于14 ℃且pH大于7.3，水质类别基本满足Ⅲ类水的要求；当WT高于14 ℃且pH小于7.3，水质类别多为Ⅳ、Ⅴ类水。该河段水质达到水功能区水质目标的时段一般在春冬两季，其原因是低温有利于氧气溶解，且低温条件下水中生物、化学需氧量较低，因此气温低的季度水质类别明显优于其他季度。

2.5 多元线性回归法分析结果

由观测期间内同一断面任意两个水质参数之间的相关系数计算结果(表3)可知，除EC与TDS外，对于DO、WT和pH 3个参数，每两个参数之间的相关系数绝对值都较大(>0.57)，说明其间存在较强的相关性；又由于DO是水质重要的指标之一，因此以DO为因变量，WT和pH为自变量，利用多元线性回归法分析三者的线性关系。

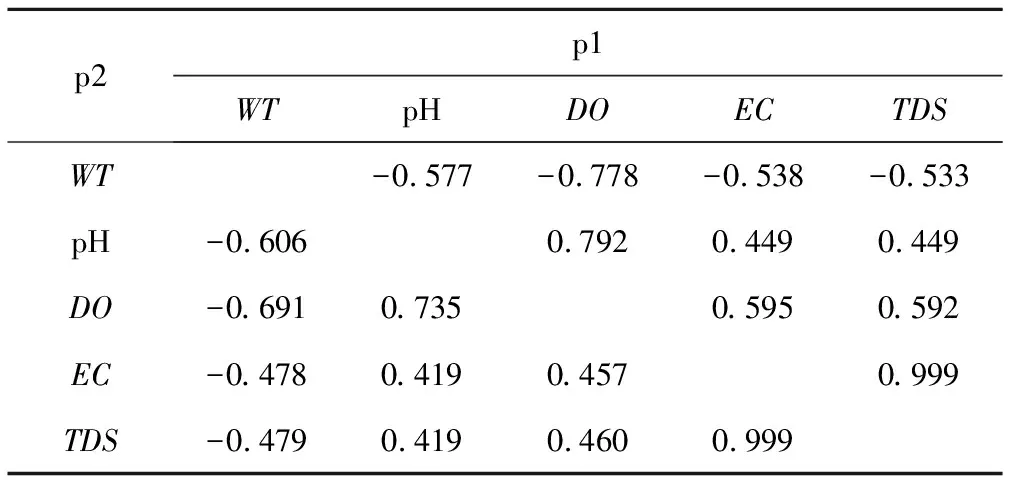
表3 p1, p2同一断面任意两个水质参数之间的相关系数计算结果

根据DO、WT和pH的观测序列，推求中间变量，将其代入标准方程式(式14)，解出待定系数，得到多元线性回归模型如下：

p1：Y=-22.603-0.213X1+4.425X2

(16)

p2：Y=-14.667-0.121X1+2.977X2

(17)

式中：Y为DO，X1为WT，X2为pH。

利用R检验公式(式15)计算两断面的R值，分别为Rp1=0.88，Rp2=0.80，可知p1，p2断面的WT、pH和DO均呈高度相关，因此上述线性回归模型可以较好反映三者之间的线性关系。其中DO与WT呈负相关，与pH呈正相关；X2系数的绝对值大于X1，说明DO受pH变化的影响大于WT；p1断面X1和X2系数的绝对值均大于p2，说明p1断面DO与WT、pH的相关性均高于p2。

3 结 论

本文基于2015年10月至2017年9月的古运河扬农化工厂河段水质参数的观测结果，采用相关系数法、变异系数法、单因子水质标识指数法和多元线性回归法对观测结果进行分析，得出主要结论如下：

(1)河段WT的变化周期性明显，pH在观测周期内的大部分时段呈下降趋势，p2断面DO低于p1，p2断面EC和TDS高于p1。

(2)上、下游断面同一水质参数总体均呈高度相关，WT接近完全相关，pH与DO的相关系数季节性变化相似，EC和TDS的相关系数几乎一致，但其季节性变化较大。

(3)同一时段的p1断面WT变异系数略大于p2；pH各季度的变异系数均小于0.1；DO变异系数季节性变化较大；同一断面EC和TDS各季度的变异系数非常接近，且大部分季度p2断面的变异系数大于p1；各水质参数的权重从高到低次序为DO>WT>TDS>EC>pH。

(4)以DO为指标的单因子水质标识指数结果表明，当WT低于14 ℃且pH大于7.3时，水质类别基本满足Ⅲ类水的要求；WT高于14 ℃且pH小于7.3时，水质多为Ⅳ、Ⅴ类水；大部分时段的p1断面水质优于p2。

(5)DO与WT呈负相关，与pH呈正相关；pH变化对DO的影响大于WT；p1断面DO与WT、pH的相关性均高于p2断面。