无刷双馈电机转子端部漏感计算及试验验证
石龙皓,刘 睿,汪世才,吴永恒,杨 波,杨 帅,印 然
(国网安徽省电力有限公司检修分公司,合肥 230009)
0 引 言
无刷双馈电机(以下简称BDFM)是一种新型的同时具有同步电机和异步电机特点的交流调速电机。与传统交流电机不同的是,控制绕组(CW)和功率绕组(PW)同时存在于无刷双馈电机定子上,并且它们的极对数不等。BDFM结构简单、运行可靠,舍弃了电刷和滑环,具有较小容量的变频器,研究前景更加广阔[1-4]。
电机的漏感种类分为三种:槽漏感、端部漏感和谐波漏感[5]。由于三种漏感种类不同,所需的计算方法也各不相同。剑桥大学的Richard McMahon教授及其课题组对一种大型BDFM进行了详细介绍。在参数计算部分,文献[6]采用了有限元法,对定子槽中的控制绕组和功率绕组进行了分块,搭建了等效电路。而Richard McMahon教授在文献[7]中更加详细介绍了转子参数的计算思路,其通过绕组函数法对BDFM进行建模,从而得出电机转子参数。
与国外相比,国内对于电机漏感的研究更加细致。文献[8]提出了各种漏感的具体计算方法,通过公式推导,将漏感计算问题归结为相对应的比漏磁导的计算,再通过计算漏磁链,得出相应的漏感值。文献[9]将此方法运用于BDFM的漏感计算,其运用逐槽累加及谐波分析的方法,解决了转子绕组设计上的多样性和不规则性所带来的计算难题。但由于线圈的自感与互感,槽、谐波、端部的比漏磁导都需要分别计算,运算量较大,而且比较繁琐。文献[10]通过对槽各层分片处理,采用数值法求出圆底槽各层间的槽漏感,它通过网络图论和回路电流法来列写关联矩阵,使各相间槽漏感可以用规范简单的方法计算出来。文献[11]提出能量摄动法,用另一种思路计算电机参数。该文指出,由于电流摄动引起磁场能量变化,通过计算系统磁场能量的摄动增量,从而得到电感参数。但是通过整体的能量变化计算漏感,需分六次进行电流摄动,还需给定转子位置角,计算过于复杂,而且没有区分槽漏感、端部漏感和谐波漏感。文献[12]是基于传统的能量摄动法,提出了一种改进后的能量摄动法,减少了非线性有限元分析的次数,提高了计算效率和精度。
鉴于以上情况,综合考虑到各种方法的优缺点之后,本文采用镜像法搭建了转子端部漏感的计算模型[13],推导出了转子端部漏感参数计算公式,并给出了相应的计算结果。最后对所得数据进行原型机试验,从而证实计算方法的可靠性。
1 转子端部漏感的计算
1.1 转子绕组结构
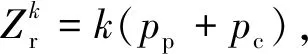
1.2 转子端部漏感
BDFM转子端部情况复杂,一方面是由于空间介质复杂,线圈穿过铁心,暴露在空气介质中,再由电机端盖封闭,同时存在多种介质;另一方面,两套极对数不同的绕组共同存在,其漏磁场互相影响的同时,又受到气隙的影响。
1.2.1 端部漏感模型
本文考虑绕组上下层关系和端部喇叭口倾角以及铁心内部线圈的影响,引入气隙电流等效气隙对端部漏磁场的作用,采用镜像法,使复杂介质统一为均匀空气介质。
建立单一线圈端部的空间结构模型,如图1所示。在三维直角坐标系中,借助极坐标与直角坐标的转换,总能获得线圈端部中层面任一端点坐标值,考虑绕组上下层关系,沿端面径向位移获得线圈端点坐标值。

图1 单一线圈端部空间结构模型
现规定线圈中电流从线圈上层边流出,从线圈下层边流入。显然,该模型满足电流连续性定理。如图2所示,端部原线圈结构以折线段ABCDEFGH表示,依次取直线段命序号m=1,2,…,7,它的镜像电流关于电机端面对称,为A′B′C′D′E′F′G′H′,依次取直线段命其序号m=12,13,…,18;气隙电流位于定转子气隙的中心处沿气隙圆周方向,被分割为线圈内部与线圈外部两段,分别为HA(线圈内部),

图2 线圈间端部互感计算模型
AH(线圈外部),分别命其序号为m=8,9,它的镜像电流为H′A′(线圈内部),A′H′(线圈外部),分别命其序号为m=19,20;嵌在铁心内部的线圈经镜像法处理,用α′,β′表示,理想模型中α′,β′为无限长直电流,实际上取为铁心有效长度的段电流即可满足计算精度,分别命其序号为m=10,11。各电流大小表达式:
式中:Im为序号为m的段电流值;N为线圈匝数;I为线圈每匝电流值;p为绕组极对数;β为短距比。
将上述20段电流细分为长度很短的若干小段,且将端部中层面作网格化处理,根据Biot-Savart定理获得线圈间端部互感计算模型。
根据模型所展现的端部线圈结构以及具体绕组的形状参数,在MATLAB中设计坐标系和绕组结构的函数,绘出转子绕组三维模型如图3所示。
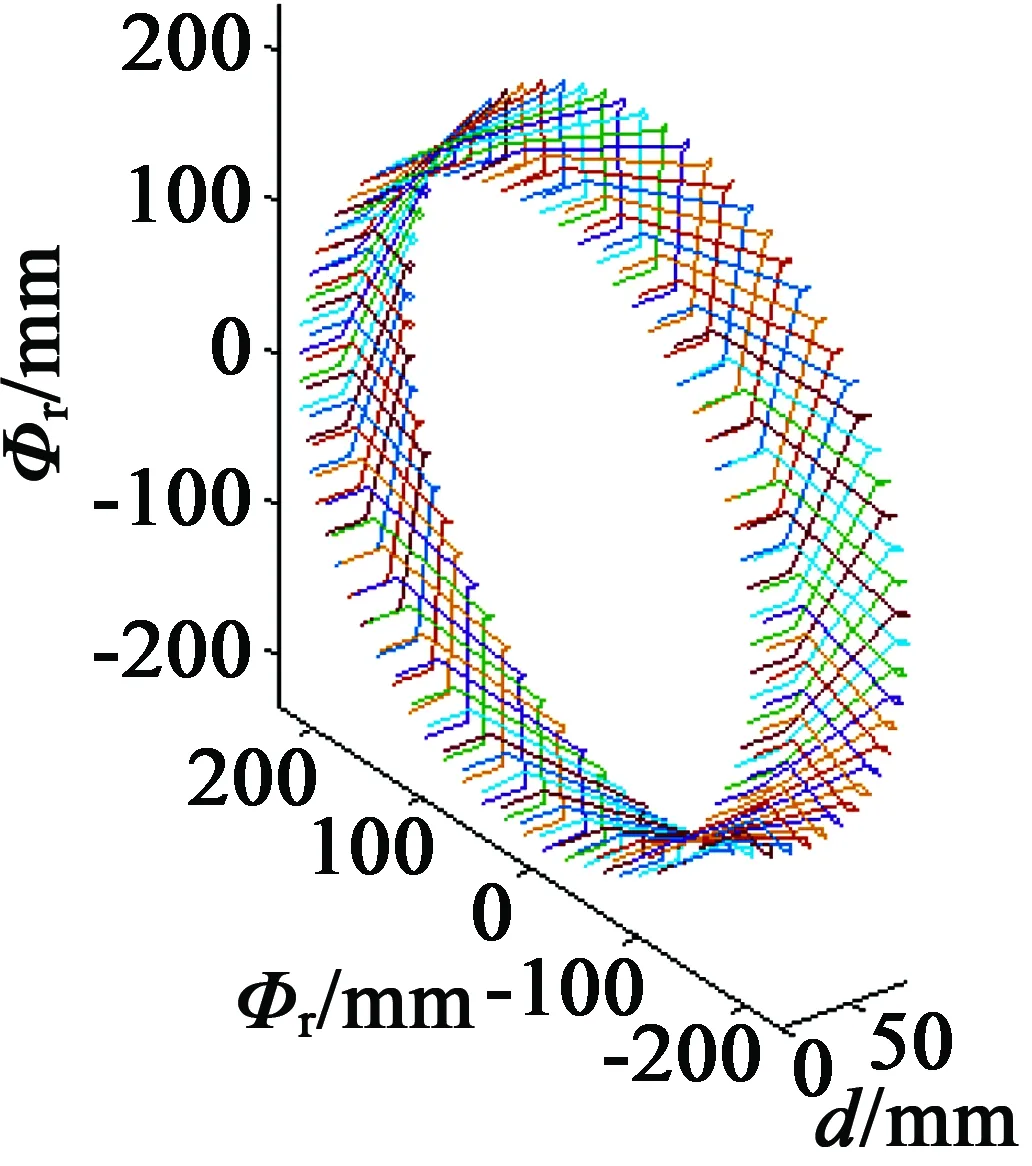
图3 BDFM转子绕组端部模型
1.2.2 端部漏感计算
根据上述模型可以计算k号线圈端部第m段与第n小段电流在j号线圈端部网格交点第g点处产生的磁通密度[16]:

k号线圈端部所有段电流在j号线圈端部网格交点第g点处产生的磁通密度:
k号线圈端部所有大段电流产生的磁通与j号线圈端部交链的磁链:
k号线圈与j号线圈的端部互漏感:
Z为单相绕组包含的线圈数,a为并联支路数,CA为A相绕组的线圈矩阵,CB为B相绕组的线圈矩阵,则A相绕组的端部自漏感:
A相绕组和B相绕组的端部互漏感:
经上述计算可得,54槽绕线式转子的端部漏感值Ld=0.477 mH。
2 原型机试验分析
2.1 原型机参数

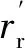

图4 实验原型机系统

参数数值参数数值定子外径Φso/mm520定子内径Φsi/mm390气隙长度lg/mm0.8转子外径Φro/mm388.4转子内径Φri/mm100铁心长度lFe/mm455定子槽数72转子槽数54自然同步速n/(r·min-1)500

图5 BDFM的等效电路图

r∗1X∗l1X∗1r″∗2X″∗l2X″∗2r′∗rX′∗lr0.0190.0851.920.0290.0846.100.0390.133
2.2 控制绕组的线电压线电流试验
本文建立了BDFM的等效电路模型并将计算值代入其中,来验证所述理论与设计分析方法的正确性。当功率绕组侧带20 kW、功率因数为0.76的阻抗性负载时,控制绕组侧的励磁线电压、励磁线电流在转速为377 r/min,426 r/min,629 r/min和702 r/min时的理论计算数据和试验数据如图6、图7所示,计算相对误差,如表3、表4所示。

图6 功率绕组恒定输出(20 kW,cos φ=0.76)时 控制绕组的励磁线电压

图7 带负载为20 kW,cos φ=0.76时 控制绕组侧的励磁线电流
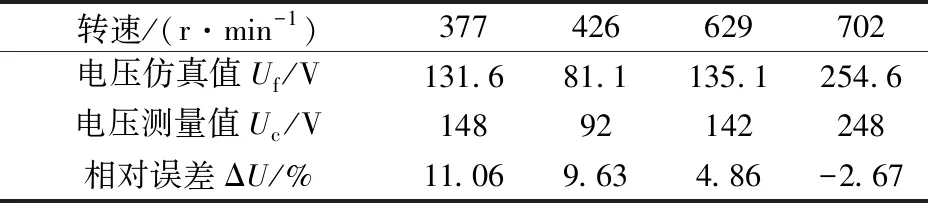
转速/(r·min-1)377426629702电压仿真值Uf/V131.681.1135.1254.6电压测量值Uc/V14892142248相对误差ΔU/%11.069.634.86-2.67
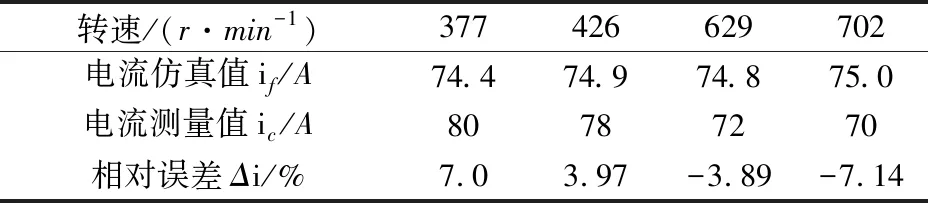
表4 线电流仿真值与测量值对比
由图6、图7、表3和表4可以看出,控制绕组线电压的理论计算数据和试验数据变化规律一致、数值相近,误差在允许的15%范围内,转子漏感的计算是正确的。同时也可以看出,理论计算数据和试验数据的相对误差具有一定的规律性。在整个电机范围运行区间内,随着BDFM转速的降低,控制绕组线电压的实测值与理论值的差值越来越大。出现这种情况,是由于BDFM转子绕组中产生的感应电流的频率随着电机转速的降低而增大,转子铁心损耗与转子电流频率之间关系为prFe1∶prFe2=(fr1∶fr2)β,prFe1,prFe2为转子铁心损耗,fr1,fr2为转子绕组感应电流频率;β为频率指数,该数值在1.2~1.6范围内,随硅钢片的含钢量而异[20]。随着铁心损耗的增大,电机铁心的饱和程度在增大,需要控制绕组提供更多的励磁电流,进而导致控制绕组线电压增大。同时,在实验过程中变频器谐波也会造成电流读数有一定的误差。
2.3 BDFM效率试验
为进一步检验转子漏感参数计算的正确性,对BDFM的效率这一衡量电机性能的重要指标进行研究。原型机对外输出有功功率与电机效率之间的关系随着转速变化,因此应针对有效转速点进行深入分析。有两个具有代表性的转速点,一个是航运部门要求的正常航行转速630 r/min,一个是处于正常航行转速和停机转速之间的700 r/min,对这两个转速点展开分析,其效率曲线如图8所示。不同转速、不同负载时电机的理论计算数据、试验数据及其相对误差如表5所示。
由图8和表5可以看出,根据BDFM的运行特点,各转速段的BDFM效率变化趋势是一致的,电机的效率先随着系统输出功率的增大而增大,然后再略有下降。对于某一转速工作时,系统最大效率点对应的功率约为该转速时系统最大可输出容量的50%。实验数据与理论曲线之间有一定的偏差,这是由于转矩传感器在实验过程中较难固定,系统对外输出转矩读数波动较大而导致的。但从图8可以看出,实验数据与理论计算值之间误差较小,且变化趋势一致。
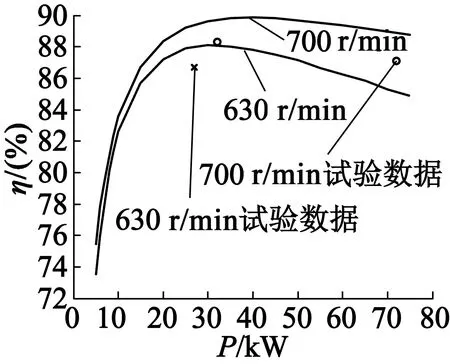
图8 不同转速点,原型机对外输出 有功功率与电机效率的关系曲线

转速/(r·min-1)630698702系统输出有功功率/kW277232功率因数0.8050.9140.84效率仿真值/%87.988.989.7效率测量值/%86.787.188.3效率相对误差/%1.382.071.59
3 结 语
本文采用镜像法搭建了转子端部漏感的计算模型,推导出了转子端部漏感参数计算公式,并给出了相应的计算结果。
由于国内外研究领域鲜有涉及BDFM端部漏感的计算方法,本文的计算方法对BDFM参数计算领域作到了有效的补充,较为准确地计算出了BDFM转子端部漏感值,对电机本体的研究具有一定的意义。
以一台2/4对极BDFM为原型机,搭建了试验平台。开展了当功率绕组侧带的阻抗性负载功率为20 kW,且功率因数为0.76时的原型机效率实验,测试了电机控制绕组的励磁线电压、励磁线电流以及电机效率。原型机试验结果验证了电机漏感参数计算的正确性。

