合情推理在豌豆杂交实验中的运用
武佳佳 李 广 刘赫健
(1 山西省忻州市第一中学 忻州 034000; 2 上海财经大学信息管理与工程学院 上海 200433; 3 北京航天航空大学北航学院 北京 102206)
科学假说是以一定的经验材料和科学事实为依据,对预期事物所做出的推测性解释。而演绎过程则是从一些假设的命题出发,运用逻辑的规则,导出另一命题的过程。而假说的得出往往要经过观察、分析、比较、联想,再经过归纳和类比,也就是我们常说的合情推理[1]。
科学思维是生物学科中培养核心素养很重要的方面。在教学过程中,不论是对现实生物学问题的数学抽象还是对复杂生物学问题的理想化数学模型的建立,都可以作为培养学生科学思维的载体。在豌豆杂交实验的教学过程中,我们往往重视假说演绎思想的渗透。的确演绎推理是证明科学结论、建立科学体系的重要思维过程,但科学结论、新思路等的发现,主要靠合情推理。合情推理和演绎推理是推理思维活动的两种基本形式。在教学实践过程中,豌豆的杂交实验不仅可以训练学生的演绎推理,同时也是训练合情推理的好素材。
1 归纳推理和演绎推理
归纳推理是从特定事实向一般事实推理的过程,是从实验重复中建立起某种确定性或规律性结论的一种认知策略。运用好归纳推理展开教学,有利于激发学生参与学习的积极性,也有助于科学思维在学科教学中的落地。
实例一: 豌豆的高茎对矮茎为显性。让杂合的高茎豌豆连续自交,F5播种后长出的高茎植株中纯合体所占的比例多少?(注: 豌豆的高茎基因和矮茎基因分别用A和a来表示,其中A对a完全显性,不考虑基因突变和其他自然选择的情况,同时所有个体都可以存活,以下实例假定条件与该实例相同。)
分析: 要求解杂合体连续自交五代后高茎植株中纯合体所占的比例,首先计算由亲本到子一代中的三种基因型的比例,再计算高茎植株中纯合体所占的比例,同理直到第五代,绘制表格如下(表1)。
根据表格,得出F5播种后长出的高茎植株中纯合体所占的比例为31/64。通过分析表格中数据,归纳推理可以得出P(AA)和P(aa)相等的结论。进一步发现,子代的前5代杂合体的概率都等于相应自交次数1/2的指数函数(即1/2n),由此猜想,杂合体连续自交n代,杂合体的概率是1/2n。
上述过程也是数学建模的过程,数学模型是用来描述一个系统或其性质的数学形式,是一种用符号、公式、图象等数学语言表现研究现象、特征和状况的研究方法[2]。在繁杂的生物学原型基础上抽离出的一个简化、理想化的数学模型,有助于学生系统地、完整地学习和理解新知识。但在模型基础上,经过数学分析得出的结论必须与具体的生物学过程相结合并加以检验[3]。所以杂合体连续自交n代,得出杂合体概率是1/2n的结论,还需要结合假定条件下的生物学过程加以分析验证。
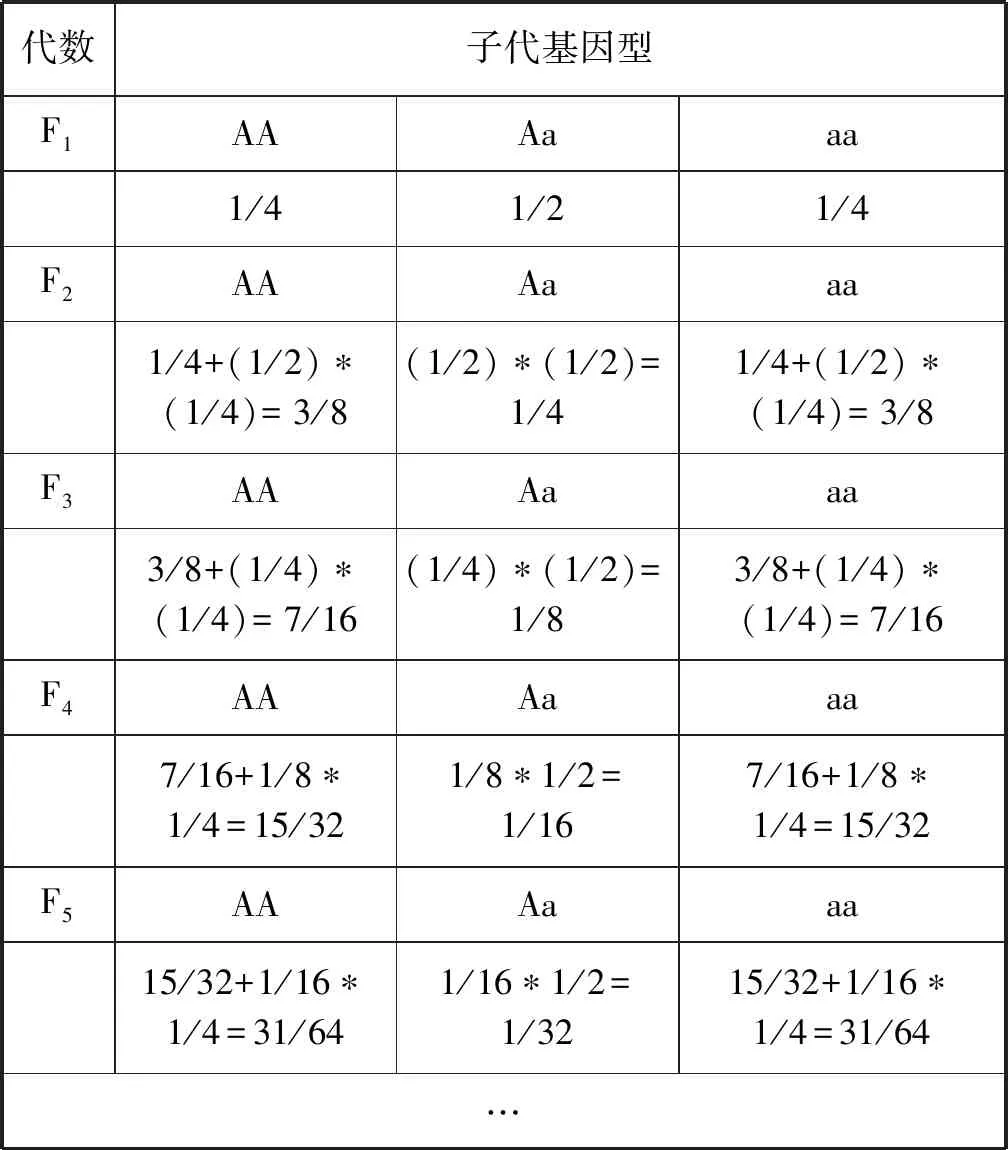
表1 杂合体(Aa)连续自交代数和子代基因型所占比例
根据生物学遗传规律,Aa逐代自交(不考虑个体死亡、迁出迁入等),后代会出现AA、 Aa、 aa三种基因型的个体,AA和aa是纯合体,纯合体自交后代不发生性状分离,仍为纯合体。而每自交一代杂合体的概率在原来的基础上再乘以1/2,所以P(Aa)=1/2n(n为Fn中的n,n是正整数),基因型为AA的个体与基因型为aa的个体数量相等,故P(AA)=P(aa)=(1-1/2n)/2(n为Fn中的n,n是正整数)。P(Aa)=1/2n(n为Fn中的n,n是正整数),基因型为AA的个体与基因型为aa的个体数量相等,故P(AA)=P(aa)=(1-1/2n)/2(n为Fn中的n,n是正整数)。
演绎推理: 当n→∞,子代中纯合体所占的比例接近于1,显性纯合体或隐性纯合体所占比例接近于1/2。杂合体的比例接近于0。这样就可以很好地解释教材中孟德尔一对相对性状的杂交实验中亲本高茎是纯合体的原因。
2 类比推理和合情推理
在合情推理的过程中,除了归纳,往往还应用类比。遗传学家萨顿运用类比的思想提出了基因与染色体的平行关系,仿生学中许多发明的最初构想都是类比生物机制得到的。豌豆的杂交实验同样也可以训练学生的类比思想。
实例二: 豌豆的高茎对矮茎为显性。让杂合的高茎豌豆连续自交,F5播种后淘汰矮茎类型,则长出的高茎植株中纯合体占的比例是多少?
分析: 根据实例一得出的结论: P(Aa)=1/2n,P(AA)=P(aa)=(1-1/2n)/2。所以在淘汰隐性纯合子之后,显性纯合子在全部植株中所占比例为: [(1-1/2n)/2]/[(1-1/2n)/2+(1/2n)]=(2n-1)/(2n+1)。题目中n=5,则显性纯合子所占比例为31/33。
实例三: 豌豆的高茎对矮茎为显性,让杂合高茎豌豆连续自交并逐代淘汰矮茎豌豆类型,F5播种后长出的植株中高茎纯合体所占比例为多少?
分析: 如同实例一采用的做法,分别计算让杂合高茎豌豆连续自交并逐代淘汰矮茎豌豆后,每一代中基因型分别为AA、 Aa、 aa各自的比例,再计算去掉矮茎之后的比例,见表2。
从实例二和实例三不难看出,第5代淘汰隐性个体和逐代淘汰隐性个体的结果是一样的。故猜想: Aa自交n代第n代去掉aa,第n代P(AA)的大小与Aa自交n代每一代去掉aa,第n代P(AA)的大小相等。
关于Aa自交n代后第n代去掉aa,第n代P(AA)的大小,可根据实例一,演绎推理得出一个计算公式P(AA)=(2n-1)/(2n+1)。类比实例一和实例二,猜想实例三可能也有一个关于n的计算公式。
结合表2,F1中P(AA)=1/3,F2中P(AA)=3/5,F3中P(AA)=7/9,F4中P(AA)=15/17,F5中P(AA)=31/33,将Fn时P(AA)记作an。猜想Fn时,an(即P(AA))=(2n+1-2)/(2n+1)=(2n-1)/(2n+1)。根据生物学遗传规律: a(n+1)=[an+(1-an)*1/4]/[an+(1-an)*1/4+(1-an)*1/2],即a(n+1)=(3an+1)/(an+3),且a1=1/3。
下面我们用数学归纳法证明此猜想。
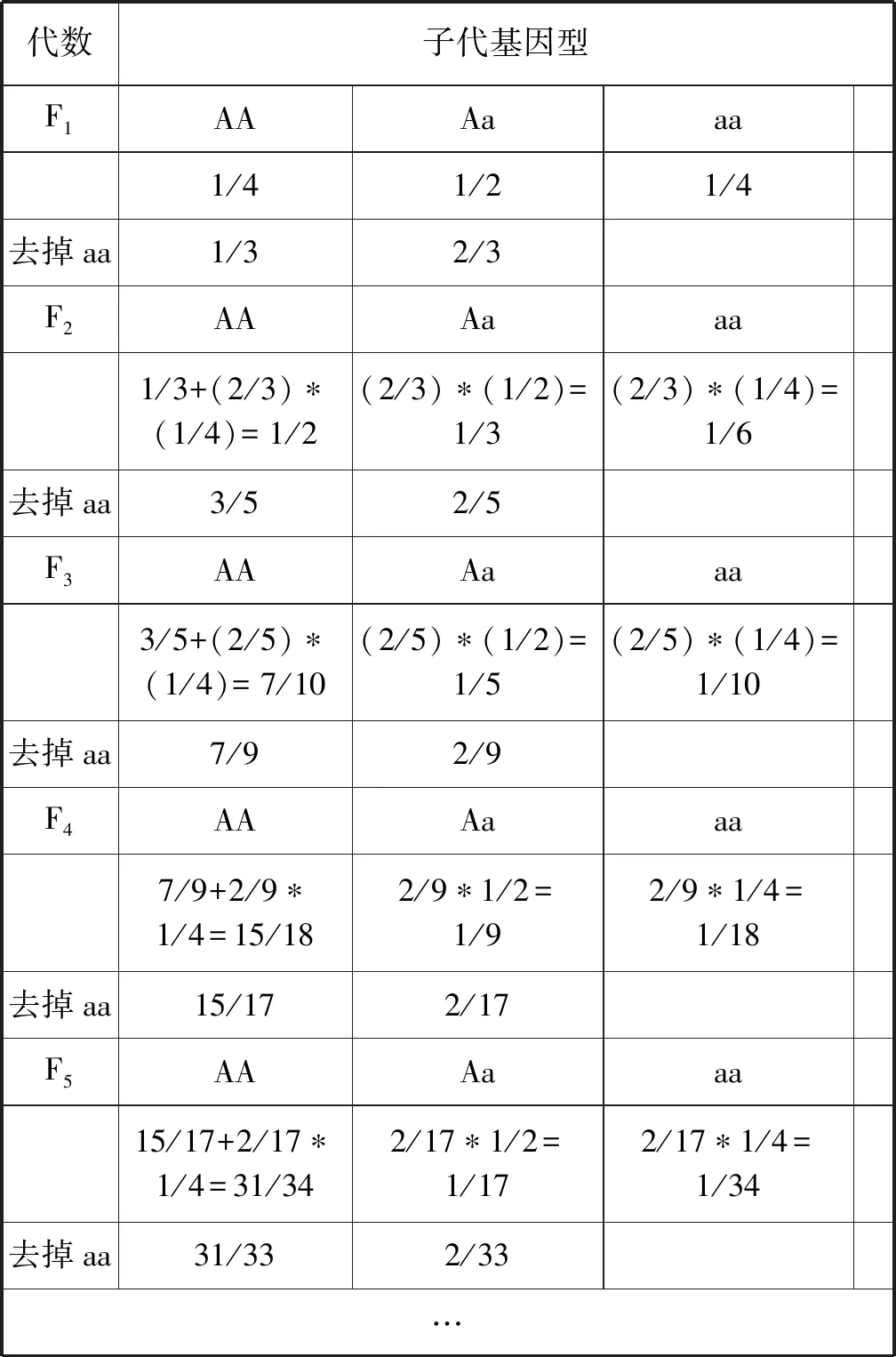
表2 杂合体(Aa)连续自交(逐代去掉aa)代数和子代基因型所占比例
(1) n=1时,a1=1/3,猜想显然成立。
(2) 假设当n=k(n∈N*)时猜想成立,即ak=(2k-1)/(2k+1),那么a(k+1)=(3ak+1)/(ak+3)=[3(2k-1)/(2k+1)+1)]/[(2k-1)/(2k+1)+3]=(2k+1-1)/(2k+1+1)。
所以当n=k+1时猜想也成立。
根据(1)(2),可知an=(2n-1)/(2n+1)对n∈N*都成立。
所以当Aa自交n代后第n代去掉aa,第n代P(AA)的值与Aa自交n代每一代去掉aa,第n代P(AA)的值相等。
3 小结
结合上面的实例,以豌豆杂交实验为素材,可以很好地训练学生的合情推理能力和演绎推理能力。合情推理和演绎推理作为推理的两种基本形式,两者是紧密联系、相辅相成的。人们在认识世界的过程中,需要通过观察实验等获得经验,也需要部分到整体的归纳和特殊到特殊的类比,同时也需要将获得的猜想加工和整理,使之条理化和系统化。合情推理和演绎推理分别在这两个环节中扮演重要角色。

