平抛运动中求时间的方法探讨

四川 张海军

一、已知水平距离求时间

【例1】如图1所示，射击枪水平放置，射击枪与目标靶中心位于离地面足够高的同一水平线上，枪口与目标靶之间的距离x=100 m，子弹射出的水平速度v0=100 m/s，子弹从枪口射出的瞬间目标靶由静止开始释放，不计空气阻力，重力加速度取g=10 m/s2。

(1)求子弹从枪口射出到击中目标靶经历的时间t;

(2)求目标靶由静止开始释放到被子弹击中下落的距离h。

【分析】题目中子弹射出后做平抛运动，根据运动的合成与分解可知，子弹的运动可分解为水平方向的匀速直线运动和竖直方向上的自由落体运动，目标靶做自由落体运动与子弹竖直方向上的运动是一致的。因此，可以根据水平方向上的速度与距离求出子弹击中目标靶的时间t。

【解析】(1)因为子弹水平方向上做匀速直线运动

所以有：x=v0t

(2)因为目标靶下落1 s时间，所以在竖直方向上

解出：h=5 m

【特点】已知平抛运动物体的初速度v0和水平距离x，而未知物体下落的高度h，则可通过水平方向的运动来求得时间。

二、已知速度偏向角求时间

速度偏向角又叫速度偏转角，在平抛运动中是指物体到达某点的末速度与初速度方向之间的夹角。

【例2】如图2所示，在倾角θ=37°的斜面底端的正上方，以初速度v0=30 m/s平抛一小球，该小球正好垂直打在斜面上，求小球在此过程中经历的时间。(已知：g=10 m/s2,sin37°=0.6,cos37°=0.8，空气阻力忽略不计)

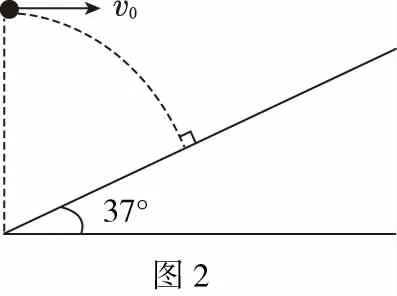
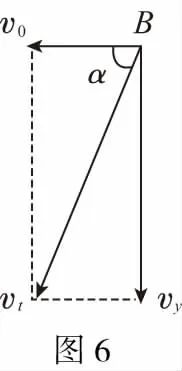
【解析】如图3所示，将小球落在斜面上的末速度vt进行分解，然后根据几何关系可以得到：

又小球在竖直方向做的是自由落体运动

则vy=gt(2)

联立(1)(2)式解得：t=4 s

【特点】在既不知道竖直高度又不知道水平距离的情况下，可通过几何关系找到速度的偏向角，从而找到求时间的突破口。

三、已知位移偏向角求时间

位移偏向角是指在平抛运动中物体到达某点的位移与水平位移的夹角。

【例3】如图4所示，从倾角为θ=37°的斜面上的A点以速度v0=10 m/s平抛一个小球。小球落在斜面上的B点，(g=10 m/s2)。求：小球从A点抛出后经多长时间落到B点。

【解析】依图5所示，小球做平抛运动

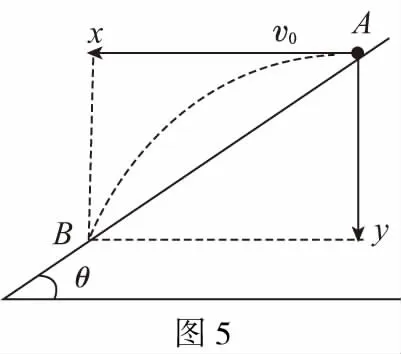
水平位移：x=v0t(1)

【特点】既无平抛运动的竖直距离又无水平距离但知道位移的偏向角，故可通过该偏向角再结合平抛运动的规律找到求时间的方法。

四、利用平抛运动的推论求时间

平抛运动中常用的重要推论有两个：(1)做平抛(或类平抛)运动的物体在某一时刻(或某一位置)，设其末速度方向与初速度方向的夹角为α，位移与初速度方向的夹角为θ，则tanα=2tanθ。(2)做平抛(或类平抛)运动的物体在某一时刻(或某一位置)，瞬时速度方向的反向延长线一定交于此时水平位移的中点。

如例3，我们也可用推论(1)求解时间。

【例4】如图7所示，将一小球从坐标原点沿着水平轴Ox以v0=2 m/s的速度抛出，经过一段时间到达P点，M为P点在Ox轴上的投影，作小球轨迹在P点的切线并反向延长，与Ox轴相交于Q点，已知QM=3 m，则小球运动的时间为多少?

【解析】由推论(2)可知Q为OM的中点，则从O点到P点的过程中，小球发生的水平位移为x

x=OM=2QM=6 m

又因为水平方向小球做匀速直线运动

【特点】水平位移、竖直位移、速度偏向角、位移偏向角均未知，但已知某时刻物体末速度的反向延长线交于该时刻水平位移的中点，则根据此推论结合平抛运动的规律便可求出相关的时间。