一类匀变速直线运动模型的拓展应用
陕西 刘秉哲
一切物体的运动都必须经历加速启动和减速停止两个运动过程。可以将这两个运动过程简化为“质点从静止开始,先以加速度a1做匀加速直线运动,达到最大速度vm后,立即以加速度a2做匀减速直线运动直到停止”,即“0—vm—0”的运动学模型。该模型及其拓展模型是运动学的常见模型,也是高考中力与运动综合问题考查的重点。下面结合自己的体会,对该运动学模型进行总结和拓展应用。
一、模型的建立和规律
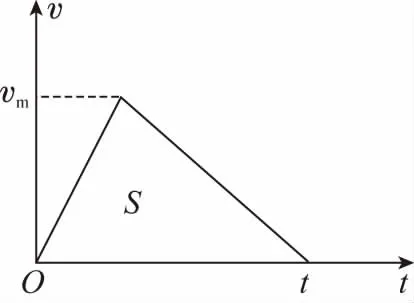
匀变速直线运动“0—vm—0”的运动学模型中各物理量的方向及其对应关系如图所示:

模型分为两个匀变速直线运动过程,涉及位移、速度、加速度以及时间四个描述运动的物理量。其中最大速度vm是该模型最重要的物理量,它既是匀加速段的末速度又是匀减速段的初速度,起到衔接两个运动过程的作用,是解决问题的关键。围绕最大速度vm,此运动模型的规律总结为:九个重要关系式和一个运动图象。
1.初速度为零的匀加速直线运动过程的重要关系式
(1)速度时间关系:vm=a1t1①
2.末速度为零的匀减速直线运动过程的重要关系式(将匀减速运动过程逆向视为匀加速运动)
(1)速度时间关系:vm=a2t2④
3.全过程的重要关系式
(1)①④两式联立得总时间:
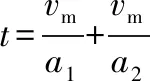
(2)②⑤或③⑥两式联立得总位移:

(3)由⑧式得总位移与总时间的关系:
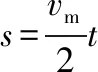
4.速度图象
二、模型的拓展及应用
【例1】一个小球从斜面顶端无初速度下滑,接着又在水平面上做匀减速运动,直至停止,它共运动了10 s,斜面长4 m,在水平面上运动的距离为6 m。求:
(1)小球在运动过程中的最大速度;
(2)小球在斜面和水平面上运动的加速度。
【解析】(1)设小球运动过程中的最大速度为vm,则小球的总路程为
解得vm=2 m/s
将匀减速运动过程逆向视为匀加速运动


【例2】跳伞运动员做低空跳伞表演,他在离地面224 m高处,由静止开始在竖直方向做自由落体运动,一段时间后,立即打开降落伞,以12.5 m/s2的平均加速度匀减速下降,为了运动员的安全,要求运动员着地速度最大为5 m/s(g取10 m/s2)。求:
(1)运动员展开伞时,离地面高度至少为多少;
(2)运动员从开始下落到着地的时间。
【解析】(1)设运动员运动过程中的最大速度为vm,将匀减速直线运动过程逆向匀加速,则有
解得vm=50 m/s
(2)运动员从开始到落地的时间为
【总结感悟】对于物体由某一速度匀加速运动到最大速度,再匀减速运动到另一速度;或由某一速度先以加速度a1匀加速到最大速度,再以加速度a2继续匀加速到另一速度等由两个匀变速直线运动组成的运动学问题,均可紧紧抓住衔接速度参照“0—vm—0”的运动学模型的规律进行解答。
【例3】如图是上海中心大厦,小明乘坐大厦快速电梯,从底层到达第119层观光平台仅用时55 s。若电梯先以加速度a1做匀加速运动,达到最大速度18 m/s,然后以最大速度匀速运动,最后以加速度a2做匀减速运动恰好到达观光平台。假定观光平台高度为549 m。

(1)若电梯经过20 s匀加速达到最大速度,求加速度a1及上升高度h;
(2)求电梯匀速运动的时间。
【解析】(1)对匀加速直线运动过程:
vm=a1t1
解得a1=0.9 m/s2
h=180 m
(2)方法一:公式法
设运动总时间为t,匀速运动的时间为t匀,匀减速运动的时间为t2,则对全过程可得:

t=t1+t匀+t2
联立得t匀=6 s
方法二:图象法
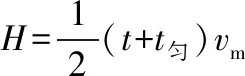
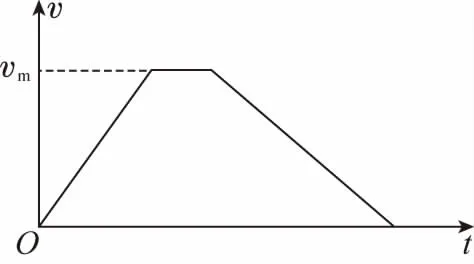
解得t匀=6 s
【总结感悟】本题相比较“0—vm—0”的运动学模型,多出了匀速运动过程,更加符合实际物体的运动情况,解答时结合匀速运动的关系式s=vt即可。
三、模型的综合应用
【例4】如图,质量m=2 kg的物体静止于水平地面的A处,A、B间距L=20 m。用大小为30 N,沿水平方向的外力拉此物体,经t0=2 s拉至B处。(已知cos37°=0.8,sin37°=0.6。取g=10 m/s2)

(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30 N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
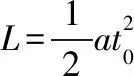
由牛顿第二定律得F-μmg=ma
联立以上两式可得μ=0.5
(2)设F作用的最短时间为t,小车先以大小为a1的加速度由静止匀加速t秒,撤去外力后,再以大小为a2的加速度匀减速到达B处,速度恰为0。对两个过程由牛顿第二定律得
Fcos37°-μ(mg-Fsin37°)=ma1
μmg=ma2
代入数据解得a1=11.5 m/s2
a2=5 m/s2
将匀减速运动过程逆向视为匀加速运动,全运动过程由运动学公式可得
解得v=11.8 m/s
对匀加速运动过程由v=a1t得
t=1.03 s
【总结感悟】对于“0—vm—0”的运动学模型及其拓展模型的综合问题,如果涉及时间和加速度,则优先选择力与运动观点解答,如传送带与板块模型。

( )
A.打到下极板上
B.在下极板处返回
【解析】带电粒子在重力作用下下落,此过程中重力做正功,当带电粒子进入平行板电容器时,电场力对粒子做负功。若带电粒子在下极板处返回,全过程应用动能定理可得
【总结感悟】对于“0—vm—0”的运动学模型及其拓展模型的综合问题,如果不涉及时间和加速度,则优先选择功能观点解答。


