基于最小理论支撑体积的模型三维打印的打印方向分析

姜晓通 郭保苏 彭庆金 刘德利

1.常熟理工学院机械工程学院，常熟，2155002.燕山大学机械工程学院，秦皇岛，066044 3.加拿大曼尼托巴大学机械工程学院，加拿大曼尼托巴，R3T 5V6

0 引言

在大部分三维打印中，模型的外部支撑结构是不可避免的，是三维打印建模的重要研究内容[1]。外部支撑结构在打印过程中起到支撑模型悬空部分的作用，完成打印后需去除。外部支撑结构的增加会增加打印模型的成本及时间，同时在去除支撑时，会影响支撑部分模型表面的质量，有时甚至会破坏模型表面，因此如何在打印过程中减小支撑结构的体积是三维打印建模的重要研究内容之一。通常情况下，模型的支撑结构体积与支撑本身的结构和模型的打印方向两个因素直接相关，因此，在支撑结构相同的情况下，支撑的使用量主要取决于模型的打印方向。打印方向会在许多方面影响打印模型的质量，如模型表面光滑度、支撑结构材料的体积、模型强度及模型打印时间等。根据考虑影响打印模型质量的因素数量，打印方向优化可以分为单一目标属性优化和多目标属性优化。

单一目标属性优化是在确定模型的打印方向时只考虑影响模型打印质量的单一属性。KATTETHOTA等[2]在确定打印方向时考虑了模型表面的光滑度。GUPTA等[3]优化了模型的打印时间，将单位球面分解为多个曲面多边形，在每个曲面多边形所定义的区间内对打印时间进行优化，计算最短打印时间对应的打印方向。大多数文献计算支撑体积这一单一目标属性来计算最优方向。KHARDEKAR等[4]在计算最优方向时采用GPU进行加速来提高算法的效率，相比CPU下的速度提高90%，且具有较好的精度。EZAIR等[5]采用与文献[3]类似的方法，在GPU下求解最小打印体积所对应的方向。HU等[6]将模型分解为多个小的组件，计算每个组件不需要或只需要少量支撑的打印方向并分别进行打印，最后将小组件组装成完整的模型。

多目标属性优化则是在确定打印方向时，同时考虑多个目标属性。SANATI等[7]在确定最优打印方向时，采用多目标遗传算法来评估模型表面粗糙度、支撑体积及打印时间等属性。BYUN等[8]同样采用遗传算法进行最优打印方向的求解，在计算最优打印方向时考虑打印时间及模型质量两个属性。与单一目标属性优化相比，多目标属性优化更加耗时[9]。

现有的打印方向计算方法并没有从理论上阐述最小支撑体积所对应方向的计算。本文将支撑体积目标属性作为优化对象，计算三维模型最小理论支撑体积所对应的打印方向。首先阐述了模型理论支撑体积的理论背景，针对离散网格模型的特点，提出了其理论支撑体积的计算方法，在计算过程中，利用光线追踪算法处理凹模型。针对理论支撑体积函数的不可导性，提出了一种基于球面坐标采样、无导数优化算法进行最优方向的计算方法。最后针对本文算法结果，从计算精度、时间及步长对结果的影响等方面对算法进行验证分析。

1 理论支撑体积计算

设三维空间中的二维流形三角网格模型M=(C,E,V)∈R3，其中，C代表网格模型中点的拓扑关系，E代表网格模型中所有边的集合，V={v0,v1,…,vn-1}(vi∈R3，i=0,1，…,n-1)是网格模型点的集合。定义S为模型的支撑结构，V(S)为支撑结构的体积。设+z为模型的打印方向，z方向上模型最低点的值为Zmin，即打印模型时的初始水平高度(打印平台在z方向上的最小值)。在三维打印过程中，模型是“自上而下”逐层成形的过程，理论上模型悬空部分的所有网格面都需要添加支撑，该支撑为网格面到打印平台的空间。然而，由于打印材料在成形过程中具有一定的延展性，模型的部分悬空网格面并不需要支撑，因此在实际打印过程中，支撑体积小于理论值。在计算模型最小支撑体积对应的打印方向时，在不确定支撑结构的情况下不能以实际支撑体积作为计算依据。由此，在实际计算过程中，通常以理论支撑体积作为计算依据来计算实际支撑体积最小时对应的打印方向。基于此，本文在确定最小支撑体积对应的打印方向时同样采用理论最小支撑体积。对于模型支撑S，其定义为

S:={(x,y,z)|z≥Zmin,∃z′>z,
(x,y,z′)∈M且(x,y,z)∉M}

(1)

式中，z′为投影点的z向值。

由式(1)可得，支撑S与模型M彼此互斥，即任何属于模型M的部分都不属于支撑S。

在计算模型给定方向的理论支撑体积时，由于网格模型并不是连续的曲面模型，其网格表面由许多离散的三角面片组成，故其求解并不是一个连续积分问题，而是一个离散积分问题。该离散积分问题求解的实质是求和所有“悬空”三角面片对应的棱柱体的体积。根据凹凸性不通，模型可分为凹面模型和凸面模型，如图1所示。在计算理论支撑体积时，它们的计算过程也不相同。图1a为凸面模型的理论支撑体积，其值为所有“悬空”三角面片对应的三棱柱体积之和。图1b为凹面模型的理论支撑体积，由于部分“悬空”三角面片对应的三棱柱并不在打印平台上，而是位于模型上，因此在计算时需要计算三棱柱与模型交点的位置。

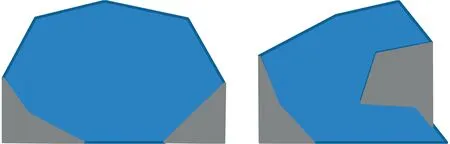
(a)凸面模型 (b)凹面模型图1 模型理论支撑体积Fig.1 Theory support volume of models

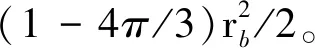
(2)

若i=k-1，则i+1=0

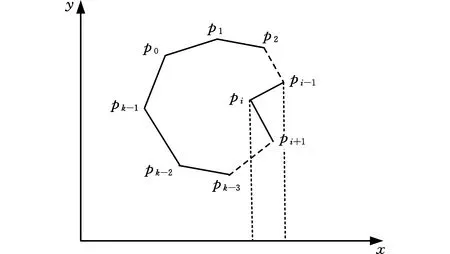
图2 多边形面积计算Fig.2 Area calculation of polygon

与多边形面积的求解相似，在计算模型的理论支撑体积时同样采用离散积分的方法。假设T为模型的一个三角面片，3个顶点分别为vi=(xi,yi,zi)，i=0,1,2。三角面片T与打印平台(打印平台的z方向左边为0)所组成三棱柱的体积计算公式为

V(T)=nz(z0+z1+z2)/6

(3)

n(T)=(nx,ny,nz),为三角面片T的非单位法矢，计算公式为n(T)=(v1-v0)×(v2-v0)。

对于凸面模型，其所有“悬空”三角面片对应的三棱柱的体积之和即为该模型的理论支撑体积，即

(4)

式中，n为模型中三角面片的个数。

对于凹面模型，在给定的打印方向，部分“悬空”三角面片对应的三棱柱的底部是落在网格模型上，而不是打印平台,因此在计算凹面模型的理论支撑体积时，式(3)并不完全适用。此时需要计算哪些三角面片对应的三棱柱的底部落在打印平台上，哪些不落在平台上。本文利用光线追踪算法判断“悬空”三角面片这一属性。

在计算机图形学中，光线追踪算法是被用来生成逼真三维场景的主要算法之一。近年来，随着可视化、虚拟现实的发展，该算法得到了越来越广泛的应用。在计算几何中，光线追踪算法被广泛应用于几何求交,但该算法在求交过程中需要较大的运算开销，运行效率较低。为了提高运算效率，在进行求交运算前，一般需要对模型进行空间划分，构建一定的空间层次结构，如均匀网格划分[10]、八叉树[11]及KD-Tree[12](一种特殊的二叉空间分割等空间划分方法)。这些空间层次结构都能够加快光线追踪的速度，本文采用最常用的KD-tree来提高光线追踪的求交速度。根据生成支撑求交的特殊性，在求交过程中只计算“悬空”三角面片在光线方向上距离模型最近的交点。设算法1为基于KD-Tree的光线追踪求交算法(图3)。根据算法1，当“悬空”三角面片对应的三棱柱的底面落在模型上时，式(3)变为

(5)

2 最小理论支撑体积所对应的打印方向计算

由于理论支撑体积函数并不光滑，故在求解最小理论支撑体积对应的方向时，并不能利用函数求导数的方法进行求解，通常需要利用无导数优化算法[13-15]来求解最优方向。此时，对于多极值函数，任意给定一个初值进行最优值求解时，其求解结果往往只是一个局部最优解，并不是全局最优解。为得到函数的全局最优解，在利用无导数优化算法进行求解前，需要确定部分可信赖区间，然后计算各个可信赖区间的局部最优值，进而得到全局最优解。

本文利用球面坐标对打印方向进行采样，以计算得到的理论支撑体积最小的前n个采样方向所在的区间作为可信赖区间，在可信赖区间内求得局部极值，再通过比较得到全局最优解。在计算最小理论支撑体积对应的打印方向前，首先讨论模型理论支撑体积函数V(S)的可导性。

2.1 理论支撑体积函数的可导性

为了简化计算，本文以凸面模型为例讨论其理论支撑体积函数的可导性。由于网格模型的理论支撑体积为模型“悬空”三角面片对应的棱柱体体积之和，因此这里只讨论其中一个“悬空”三角面片T对应的三棱柱体积函数V(T)的可导性。当T绕着x轴旋转角度θ时，式(3)中的zi变为zicosθ+yisinθ(i=0,1,2)，nz变为nzcosθ+nysinθ，则式(3)变为体积关于转角θ的函数：

算法 1:光线追踪求交输入: (1)pNode:与网格模型M相关联的Kd-Tree(2)vOrigin:光线追踪源点(3)vDirection:光线方向输出:(1)fNearest:浮点数,初始值为FLT_MAX(2)vHit:光线与模型的交点(3)nHitTri:交点所在的三角面片 执行:bool rayIntersection(pNode, vOrigin, vDirection, fNearest,vHit, nHitTri){ Point pHit; bool bHit = isIntersection (pNode, vOrigin, bHit); //判断光线与pNode的包围盒是否相交 If (isLeaf(pNode))If(bHit) Triangles=GetTriangleID (pNode); //得到节点pNode内的三角面片 bool bHitTri = IsInsectionTri (Triangle,vOrigin, vDirection, pHit); //判断光线与三角面片是否相交,若相交则得到交点pHit If(bHitTri&&dis(vOrigin, pHit)pLeft, vOrigin, vDirec-tion, fNearest,vHit, nHitTri); bool bRight =rayIntersection (pNode->pRight, vOrigin, vDi-rection, fNearest,vHit, nHitTri); If(bLeft | |bRight)return true; return false;}

图3光线追踪求交算法

Fig.3Raytracingintersectionalgorithm

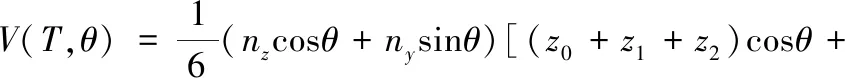
(6)

式(6)变形后为

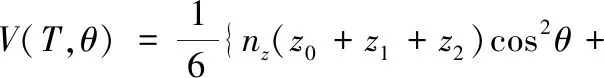
(7)

为了进一步简化计算，这里假设T的初始位置与水平面平行，则式(7)可以简化为

(8)

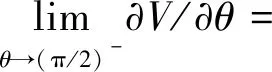
(a)立方体模型 (b)RockArm模型图4 测试模型Fig.4 Test models

2.2 基于无导数优化算法的最优方向计算

2.2.1球面坐标采样

在利用无导数优化算法求解最优打印方向前，首先需要确定求解的部分可信赖区间。由于本文算法的求解目标为打印方向，因此采用球面坐标的方法对空间方向进行采样，计算每个采样点对应打印方向的理论支撑体积，选择体积最小的前n个方向对应的区间作为无导数优化算法求解的可信赖区间。

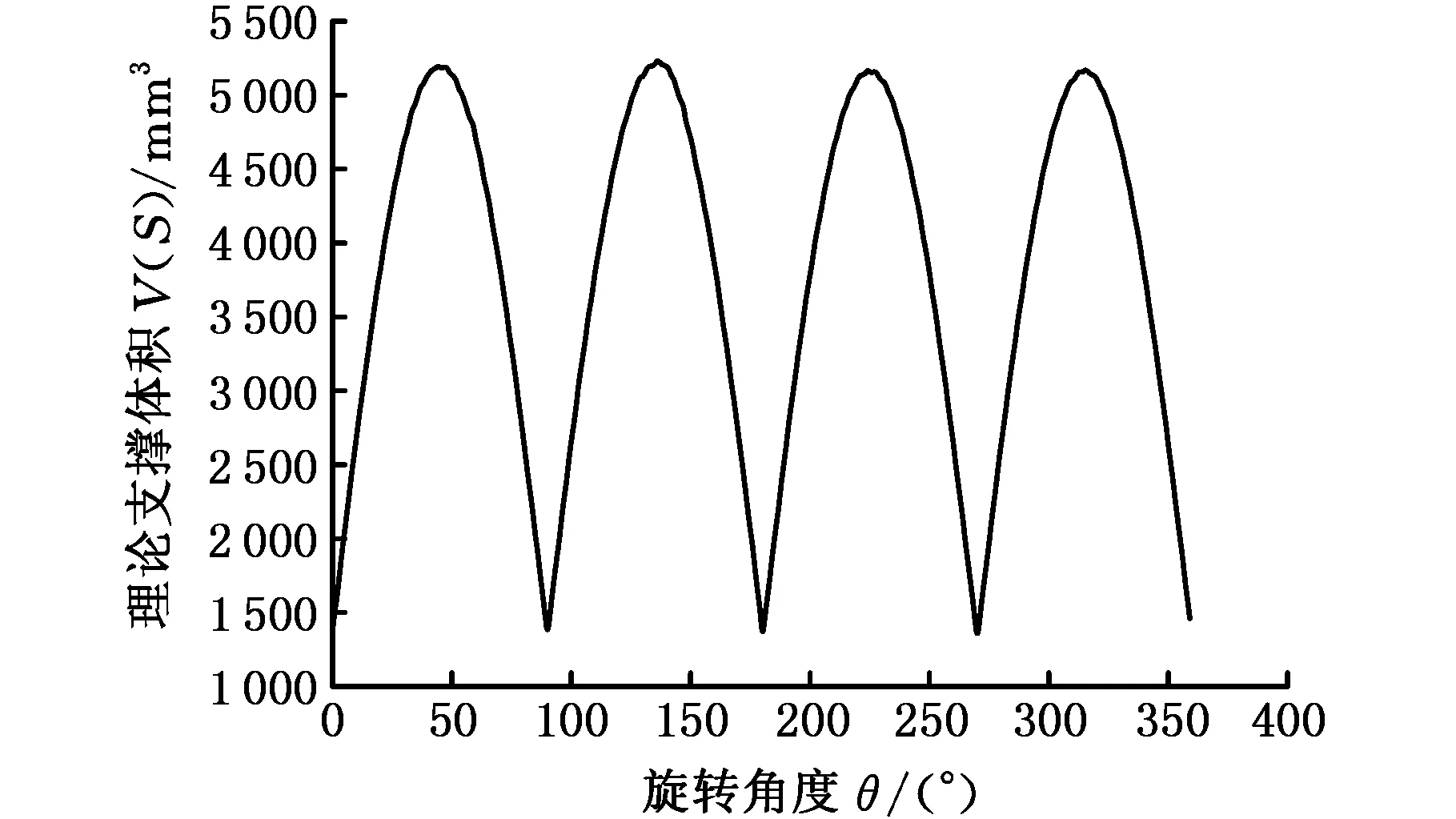
(a)立方体模型

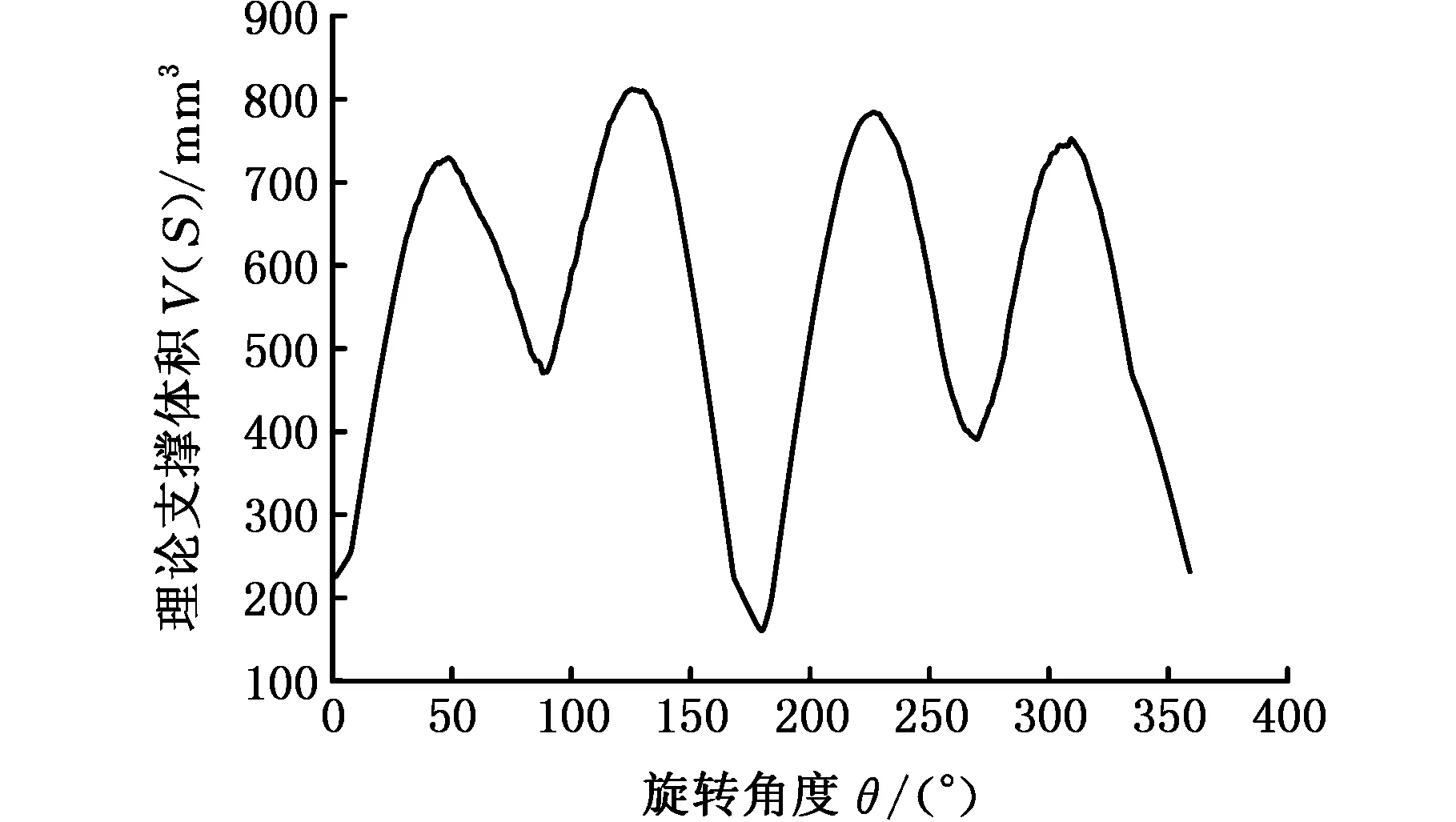
(b)RockArm模型图5 模型理论支撑体积曲线图Fig.5 Curve graph of models’ theory support volume

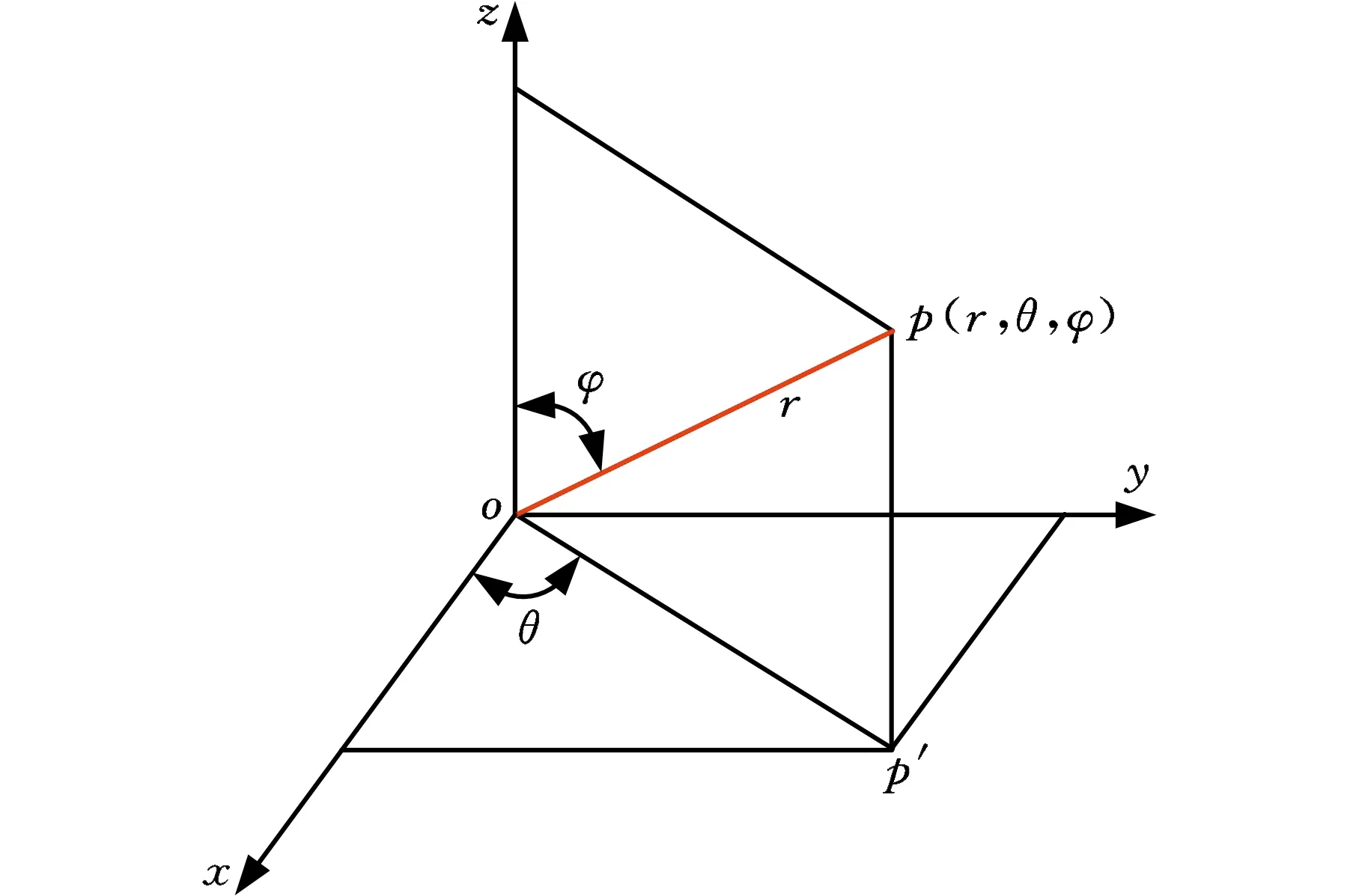
图6 球面坐标示意图Fig.6 Schematic diagram of spheroidal coordinates

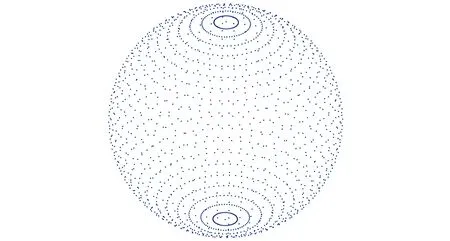
图7 球面坐标采样结果Fig.7 Results of spheroidal coordinate sampling

球面坐标以坐标原点为参考点，由方位角、仰角及距离构成。如图6所示，假设p(x,y,z)为三维空间内一点，则点p的空间位置可用3个有次序的数(r,θ,φ)来确定，其中,r为原点o与点p间的距离，θ为从正z轴来看自x轴按逆时针方向转到op′所转过的角，φ为有向线段op与z轴正向的夹角，这里p′为点p在xoy面上的投影。r、θ、φ的取值范围分别为：r∈[0,+∞)，φ∈[0,2π]，θ∈[0,2π]。球面坐标采样的实质为对θ及φ方向进行球面坐标均匀采样，并利用一定的转化关系将其转化成直角坐标系内的空间点。以图6中的点p为例，该转化关系为：xp=rsinθcosφ，yp=rsinθsinφ，zp=rcosθ。这样，在三维空间内生成一系列的采样点pi(xi,yi,zi)，则其采样方向opi=(xi,yi,zi)。图7为利用球面坐标生成的采样点，在生成采样点过程中，在θ及φ方向上进行步长为6°的采样，共得到1 800个采样方向，然后计算每个采样方向对应的理论支撑体积。

2.2.2基于无导数优化算法的方向优化

在对打印方向进行采样并计算对应的理论支撑体积后，将最小的几个理论支撑体积对应的采样打印方向作为初始值，利用无导数优化算法在选定的采样方向对应的可信赖区间内计算局部最优方向，则计算得到的所有局部最优方向的最小值为全局最优方向。在利用无导数优化算法计算局部最优解时，求解的可信赖区间是保证算法能够收敛的基础。当区间过大时，区间内部可能会有两个甚至更多的极值，利用无导数优化算法得到的局部最优解不可信。该区间的大小取决于采样步长，为了保证计算区间可靠，计算收敛，采样时步长不宜过大。

无导数优化算法可以分为有限差分方法[13]、基于模型的方法[14]、模式搜索方法[15]等3种方法。模式搜索方法是一种直接的局部搜索方法，在搜索过程中直接使用函数值，并不需要评估函数的导数。该算法的基本思想从几何意义上来说，是寻找具有较小函数值的“山谷”，通过迭代的方法使搜索沿着“山谷”的走向来逼近极小值。该算法从给定的起始点开始，通过局部移动寻找下降的方向来得到局部的最优值，其最经典的算法为坐标搜索。坐标搜索是一种无约束的优化求解算法，求解目标函数f(x)的最小值。在计算时首先选定一个初始值及步长，然后通过迭代的方法得到一个局部最小值。本文在计算最优打印方向时，同样是找到最优打印方向所对应的球面坐标，初始化值为上面所计算的最小的几个理论支撑体积所对应的方向，步长阈值为1°。在每个作为初始值的方向上，利用坐标搜索算法得到局部的最小理论支撑体积。这些局部最小理论支撑体积的最小值所对应的打印方向即为最优的打印方向。

3 实验结果分析

本文算法开发环境为VS2008，编程语言为C++，基于OpenGL图形库进行模型显示，测试用电脑的处理器为Inter Core 10 ms i5-2500，主频为3.30GHz，内存为4GB。本节主要从算法的精度及计算时间两个方面来验证本文算法的有效性与实用性，同时分析采样步长对计算结果的影响。在计算过程中，为了加快运算速度，采用OpenMP技术进行并行运算，以提高运算效率。

3.1 理论支撑体积的计算精度与计算时间

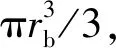
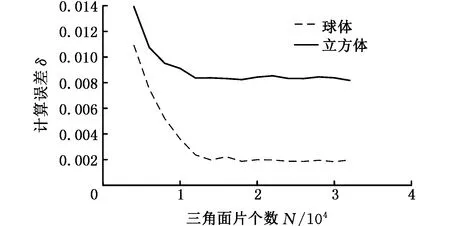
图8 理论支撑体积的计算误差Fig.8 Calculation error of theory support volume

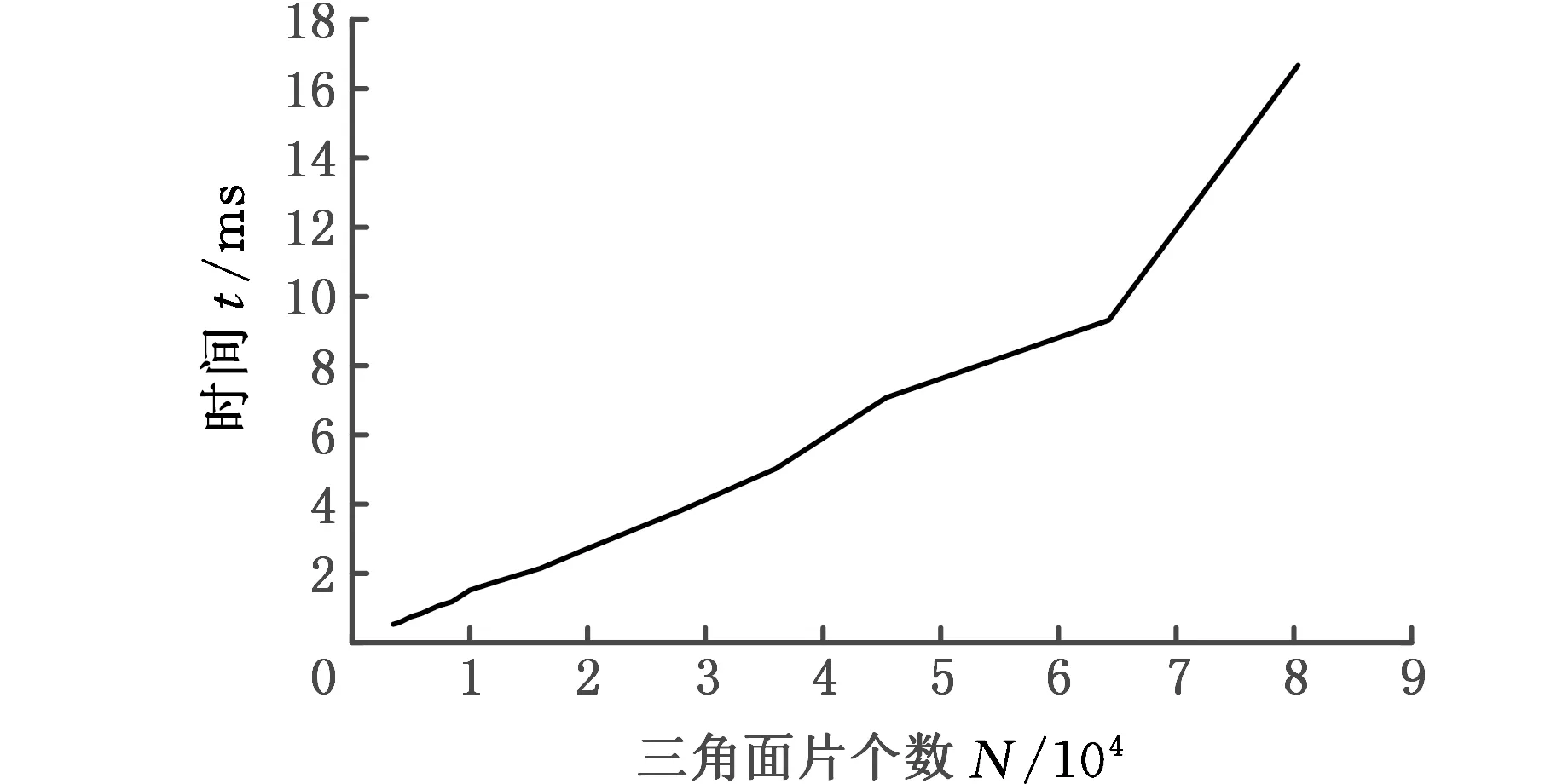
图9 理论支撑体积的计算时间Fig.9 Calculation time of theory support volume

图9所示为理论支撑体积的计算时间与模型三角面片个数之间的关系。测试所用的模型为图4b的RockArm模型，且在测试过程中模型的网格数不断增加。对于每个测试模型，在测试过程中的采样步长为10°，共648个采样方向。模型在每个采样方向上都进行理论支撑体积的计算，然后得到单次计算的平均时间。由图9中的曲线可得到，单次理论支撑体积的计算时间与模型三角面片个数成线性关系，随三角面片个数的增加而增长。当三角面片个数为70 000时，计算时间为10 ms左右，完全能够满足时间要求。

3.2 采样步长对计算结果的影响

在计算过程中，采样步长会对计算时间及最终的优化结果产生较大影响。这里利用不同的采样步长来测试其对计算结果的影响。

图10为采样步长对采样时间及优化时间的影响曲线，测试模型为图4b的RockArm模型，测试所用的采样步长分别为2°、3°、4°、5°、6°、9°、10°、12°、15°、18°、20°、22°、25°、30°、36°、45°、55°、60°、80°、90°、180°。在利用无导数优化算法进行优化计算时，计算理论支撑体积最小的前100个采样方向，在这100个采样方向确定的区间内进行优化计算。由图10可以得到，对于采样时间，当采样步长增大时，采样方向减小，在单次计算时间一定的情况下总的采样时间缩短。对于优化时间，当采样步长较小时，在优化方向数量确定的情况下，由于优化区间较小，单次优化时间也会缩短，因此总的优化时间也较短。随着采样步长的增大，优化区间增大，优化时间也会相应增长。当采样步长为25°时，采样方向的数量刚好为100，此时理论上的优化时间应该最长。在实际采样过程中，由于模型的初始位置不同，用于局部优化的各初始方向也不同，单次优化时间也会所有变化，因此最长优化时间对应的采样步长约为25°，但会有所波动。当采样步长大于25°时，采样方向的个数小于100，随着采样步长增大，采样方向的个数也随之减少，因而优化时间也随着减短。

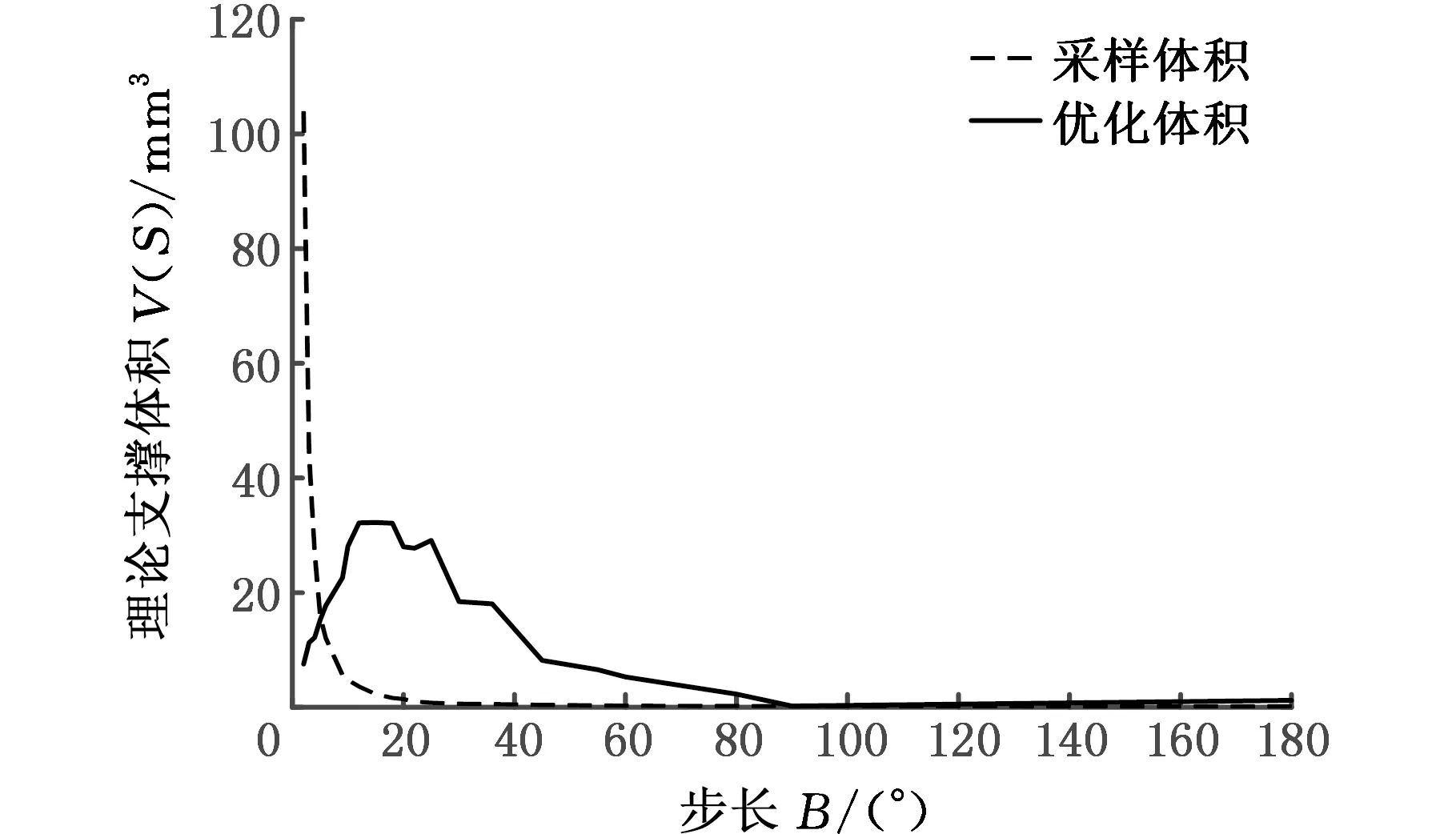
图10 不同采样步长的测试时间Fig.10 Test time of different sampling step

图11所示为在不同采样步长下，采样得到的最小理论支撑体积与优化后得到的最小理论支撑体积。从图11中可以得到，当测试过程中的采样步长足够小时(采样步长的数值为2°、3°、6°时)，经采样得到的最小理论支撑体积即为优化后的最小理论支撑体积，不需要后续的优化即可得到最优打印方向；当采样步长较大时需要利用优化算法才可得到最优的打印方向；当采样步长超过一定的值时，即使利用优化算法也得不到最优打印方向。

图11 不同采样步长的计算结果Fig.11 Calculation results of different sampling step

表1所示为不同网格模型的测试对比结果。在测试过程中，采样步长为5°，共计算36×72=2 592个方向的理论支撑体积。在优化过程中，选取理论支撑体积最小的前100个方向进行优化计算，分别计算模型三角面片个数、网格模型体积V(M)、最优采样方向理论支撑体积、最优方向理论支撑体积、采样时间及优化时间。从表1中的计算结果可以得到，计算时间随着模型三角面片个数的增加而增长。当模型网格数量较小时，本文算法效率非常高，即使模型三角面片个数为200 000，计算时间也短于180 s。当模型三角面片个数太多时，可先对模型进行基于特征的简化，减少模型三角面片个数，然后再进行打印方向的优化。为了进一步验证本文算法有效性，将本文算法与Autodesk公司的Meshmixer软件进行对比测试。在进行对比测试时，除了一个模型外，其余所有模型的最终打印方向与本文算法的结果基本一致，如图12所示。在得到各自的最优打印方向后，利用Meshmixer软件提供的算法生成树状支撑结构，分别计算两个不同最优打印方向下的实际支撑体积。从结果可以看出，对于该测试模型，本文算法结果更优。

表1 不同模型测试结果

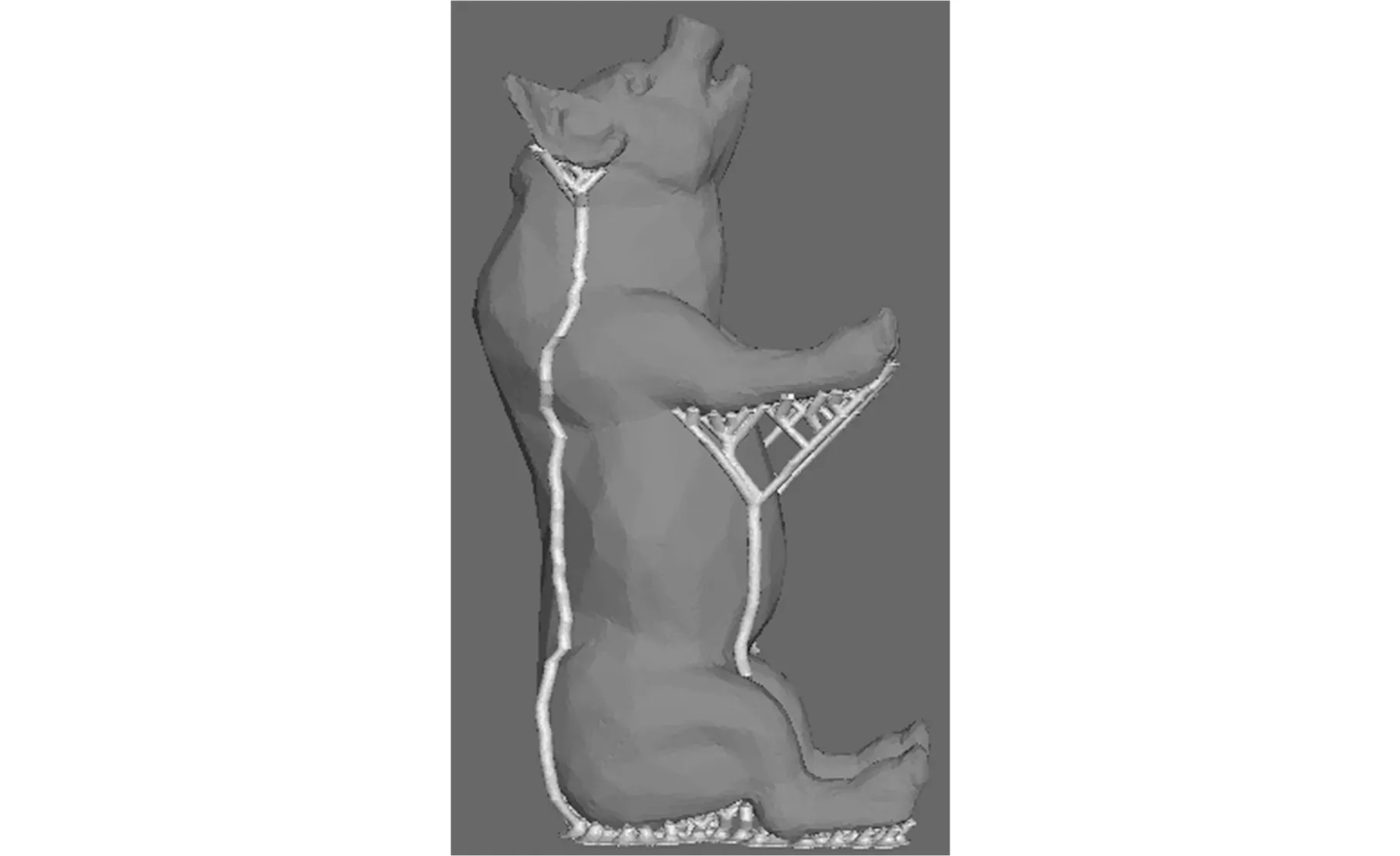
(b)本文算法计算结果图12 结果比较Fig.12 Comparison of results

4 结论

(1)本文提出了一种基于最小理论支撑体积的模型三维打印方向的计算方法，该方法能够快速准确地计算最小理论支撑体积所对应的模型打印方向，为模型三维打印方向提供了辅助的优化方案。

(2)阐述了模型理论支撑体积的理论背景，给出了离散网格模型理论支撑体积的计算方法，同时针对凹模型的理论支撑体积的特殊性，利用光线追踪的方法来计算凹模型的理论支撑体积。

(3)针对理论支撑体积函数不可导的特点，利用无导数优化算法来计算最小理论支撑体积所对应的方向，该方法可采用并行运算以加快计算速度。

(4)实验表明本文算法在计算精度和计算效率上都优于已有的方法。

本文算法在计算方向时只考虑支撑体积这一单一因素，下一步研究将进一步考虑三维打印的表面粗糙度、打印时间等多方面因素，增强算法的适用性。