基于概率分布的异常检测模型训练方法
裘 昱
安徽省军区数据信息室,安徽合肥,230000
异常检测是入侵检测的一个重要方面[1]。入侵检测是通过检测各类系统数据(如网络数据包、系统日志等)来区分正常数据与异常数据,从而保护计算机系统的一种网络安全技术。对传统异常检测模型的训练,需要用一个“完全干净”(不含异常数据)的数据集来对检测模型进行训练[2]。这种方法存在几个方面问题:(1)这种数据集通常很难得到;(2)如果数据集中包含有某些异常数据,由此得到的检测模型将无法检测出此类异常数据;(3)这种模型将很难“在线(online)”训练,因为无法保证“在线”时的训练数据满足要求[3]。为此,本文提出了一种基于概率分布的,无须“完全干净”的数据集就能够进行异常检测模型训练的方法。
1 异常检测
1.1 数据集模型
本文使用“混合数据(正常和异常数据均存在)集”来表示训练用数据集。在这个“混合数据集”中,每个数据元素均可以表示为:若它的出现为小概率λ,那么它是个异常数据;或者它的出现为概率(1-λ),那么它是个正常数据。
本文假设,一个任意给定的系统程序运行序列,如果此序列发生的概率为(1-λ),则它是一个正常的系统调用序列,即为正常数据;如果一个系统程序运行序列发生的概率为λ,那么它是个异常的系统调用序列,即为入侵数据。
在本文的方法中,数据集中的某个数据元素xi,要么它属于概率为(1-λ)的主分布M(Majority),要么它属于概率为λ的异常分布A(Anomalous)。这样,对于整个数据集D,则有:
D=(1-λ)M+λA
(1)
因此,数据集D就被分为两个子数据集:正常数据的数据子集(简称正常数据集)和异常数据的数据子集(简称异常数据集),本文使用Mt(At)来表示对数据元素xt分类之后(即t时刻)的正常(异常)子数据集。初始时,没有任何异常数据被检测,所以M0=D,A0=φ。
1.2 概率分布模型
可以使用任何一种机器学习算法来得到概率分布模型。对于正常数据集,有函数lm,其输入是正常数据集中的数据元素mt,输出是该数据元素的概率分布Pmt。同样,对于异常数据集,有函数Ia,其输入是异常数据元素at,输出是该异常数据的概率分布Pat,即:
Pmt(x)=lm(mt)(x)
(2)
Pat(x)=la(at)(x)
(3)
对于函数lm和la,可以是任何概率模型生成算法(如朴素贝叶斯算法等)。注意,由于异常数据集初始化时为空,对于概率模型生成算法la来说即没有数据用来训练,因此,Pat实际上是一个先验概率分布。
1.3 异常数据的检测
在本文的方法中,异常数据的检测等同于判定一个给定的数据元素是属于分布A还是属于分布M,并据此将该数据元素放入相应的数据子集中。
在时刻t,数据集D分布的可能性L(Likelihood)定义为:
(4)
为了计算方便,使用对数来简化计算,由此得到LL(Log Likelihood)的计算方法:
(5)
判定某个数据元素是否是异常数据,即判定它在特征空间中是否为奇异点(outlier)。
算法如下:
(1)对于一个给定的数据元素xi,计算其从主分布Mt-1移至异常分布At-1之后的LLt的值,并计算该值与移动之前的LLt-1值的差值。即:
Mt=Mt-1{xt}
(6)
At=At-1∪{xt}
(7)
K=LLt-LLt-1
(8)
(2)设定阈值c,如果K值大于阈值c,则判定此数据元素为一个异常数据,并将它从正常数据集移至异常数据集,否则,此数据元素保留在正常数据集中。即:
Mt=Mt-1
(9)
At=At-1
(10)
(3)对数据集D中所有的数据元素重复上述过程,最后,得到从原数据集D分解出的两个数据子集:正常数据集和异常数据集。
这里阈值c的选择会影响到模型对异常数据的检测。c值越小误报律会下降,但检测率也会随之下降;c值越大,检测律上升的同时也带来了误报律大的问题[4]。
2 异常检测
2.1 数据集描述
本文所使用的两个数据集是在两台计算机上采集到的系统程序调用序列(包括正常程序和入侵程序)的记录集。
第一个数据集来自MIT Lincoln Labs(麻省理工学院林肯实验室),数据为某部装有Solaris操作系统的计算机一段时间内的系统程序调用记录。其中包含的异常数据来自3个入侵程序:eject、ps(LL)和ftpd。
第二个数据集来自University of New Mexico(新墨西哥大学),数据为操作系统15个月内的系统程序调用记录。其中包含的异常数据来自4个入侵程序:named、xlock、login和ps。
表1和表2是这两个数据集的基本信息汇总。
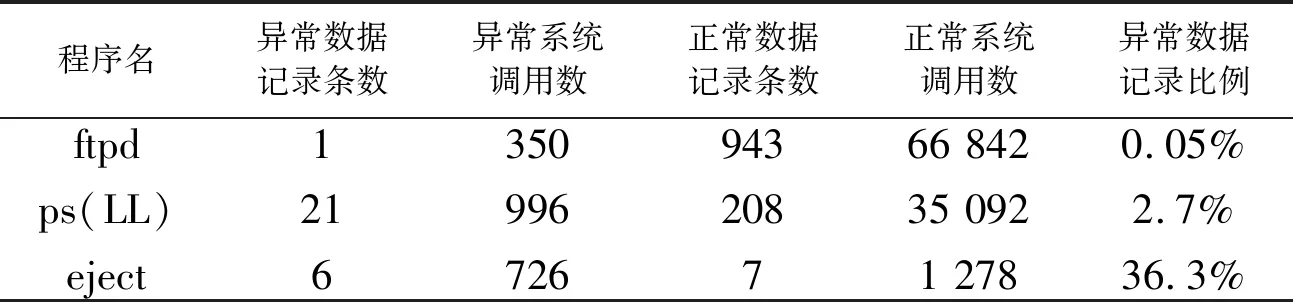
表1 Lincoln Labs数据集基本信息
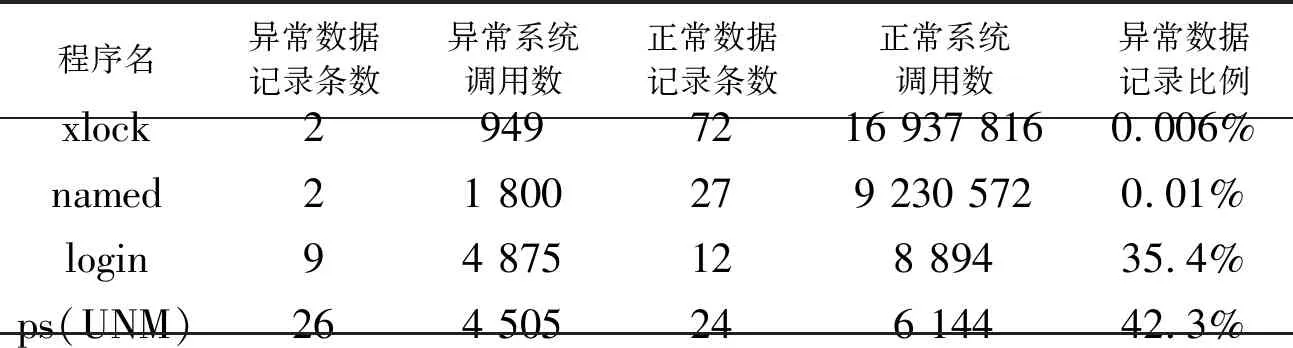
表2 University of New Mexico数据集基本信息
2.2 异常检测
假设异常数据记录的产生是随机的。对于la函数,在时刻t能够得到异常概率分布Pat。对于lm函数,本文使用定阶马尔可夫链(Fixed Order Markov Chain) 算法,在正常数据集上得到正常概率分布Pmt。
其概率模型的建立方法是:对于某个给定的系统调用序列xt,在长度L(L值事先确定)的系统调用序列后,若出现了xt,便计数一次。也就是说,它是某个特定程序的前L个系统调用后的条件概率。即:
P(Xt|Xt-1,Xt-2,…,Xt-L)
(11)
为了避免概率为0的情形出现,对每个计数初始化为一个非常小的值(0.01),并设置L=3。
原则上,必须在处理每一个数据之后,重新对机器学习算法来训练,以得到LL值。但实际上只需对拥有同样前缀的数据进行计算,因此,对数据集D只需扫描两次。第一次扫描假设所有元素都是正常数据,得到各种系统调用序列的概率分布;第二次扫描是计算当一个数据判定为异常数据时的K值。
2.3 算法比较
STIDE算法和t-STIDE算法有着良好的入侵检测效果[5]。它们用于训练和测试的数据集是从表2数据集中抽取出的正常数据记录。
STIDE(sequence time-delay embedding)算法对在训练集中看到过的系统调用序列(序列长度为6)在测试集中进行扫描。它认为任何一个在训练集中没有看到过,而出现在测试集中的系统调用序列即为异常。t-STIDE算法是STIDE算法的变种,它使用一个阈值,只有当某个数据在训练集中未出现过,但在测试集中出现了,且数量超过这个阈值(通常为数据总数的0.001%)时,才认为它是一个异常。
2.4 实验结果
实验对比主要考查两个指标:检测率(intrusion detection rate)和误报率(false positive rate)。


检测率反映的是模型的正确性,误报率反映的是模型的健壮性,通常检测模型必须在这两者之间寻求平衡。针对某一确定的训练/测试数据集,用得到的ROC(Receiver Operating Characteristic)曲线来反映检测率与误报率之间的关系。
首先,将本文的算法与上述两个算法在同一个混合数据集(异常数据的总数不超过数据总数的5%)上进行训练。接着,将本文的算法在混合数据集(异常数据的总数不超过数据总数的5%)上进行训练,对两个比较算法使用正常数据集进行训练,结果分别见图1和图2。
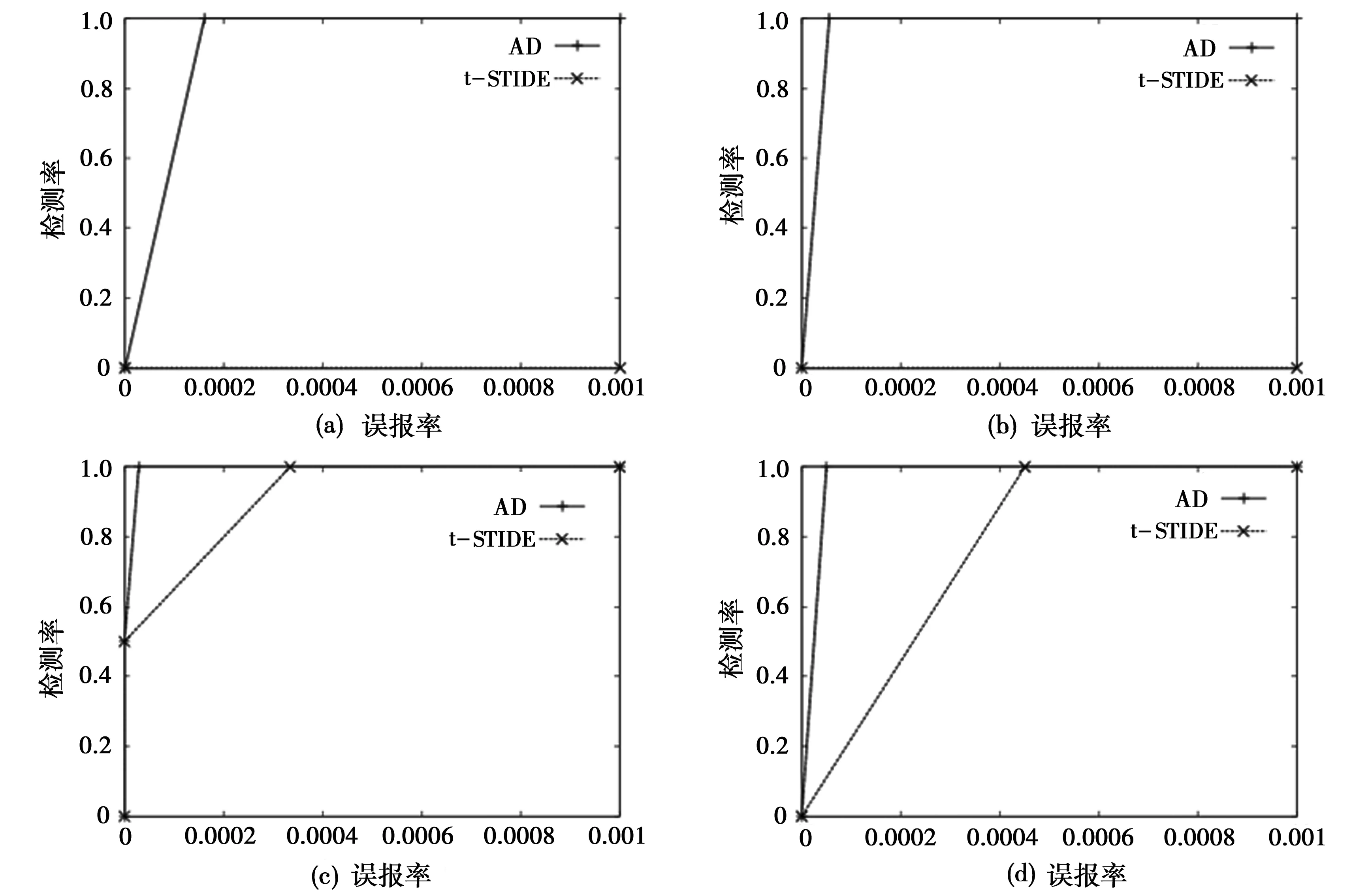
图1 本文方法与t-STIDE算法的检测效果比较(a)-(d)分别代表四种入侵程序产生的异常数据的检测情况,其中(a)ftpd,(b)ps,(c)xlock,(d)named
(1)实验1:同时使用混合数据集。对于STIDE和t-STIDE算法来说,这个数据集既是训练集也是测试集。结果,STIDE算法没有检测出任何异常数据,原因是对于STIDE算法来说,测试集中的所有系统调用序列(正常与异常数据)在训练集中都曾经见过。对于t-STIDE算法,由于阈值必须事先根据数据元素总数(这在实际环境下是不可能事先知道的)决定,所以并不能保证设定的阈值是正确或合适的,比如对于由入侵程序ftpd和ps产生的异常数据,算法就没有检测出来。本文算法与t-STIDE算法的检测效果的比较见图1。图中,本文算法的ROC曲线用AD标识。
(2)实验2:本文算法使用混合数据集,STIDE和t-STIDE算法使用正常数据集。STIDE算法和t-STIDE算法使用正常数据集中的1/3数据进行训练,余下的作为测试用数据。检测效果的比较见图2。图中,本文算法的ROC曲线用AD标识。

图2 本文方法与STIDE算法和t-STIDE算法的检测效果比较(a)-(d)分别代表四种入侵程序产生的异常数据的检测情况,其中(a)ftpd,(b)ps,(c)xlock,(d)named
可以看出,图1中本文提出的算法具有较优的检测效果。图2中本文的算法在检测效果上与其余两个算法不相上下。总体上,本文提出的基于概率分布的异常检测模型训练方法具有较好的检测效果。
3 几点假设
本文提出的异常检测的方法是基于以下三点假设[6]:
(1)对于正常数据,可以建立它的概率分布模型。
(2)异常数据从本质上与正常数据不同。
(3)训练数据集中的正常数据从数量上远远超过异常数据。
对于系统程序调用来说,正常的调用过程应该非常有规律并能有效地建立模型。由于异常数据是以入侵为目的,它们调用过程往往较为特殊,这就有条件将它们检测出来[7]。
对于第三个假设,本文也做了进一步的研究,方法是调整数据集中的异常数据总数,来观察不同比例下的异常数据的检测效果,如图3。实验结果显示,随着异常数据所占比例的增加,模型的检测能力明显下降。从图3中可以看出,对于含有较少的异常数据(这些数据记录由ftpd、ps(LL)、xlock和named软件生成)的数据集,算法模型拥有较好的检测能力。当数据集中含有较多的异常数据时(这些异常数据记录由login、ps(NUM)软件生成),算法模型的检测能力下降明显。
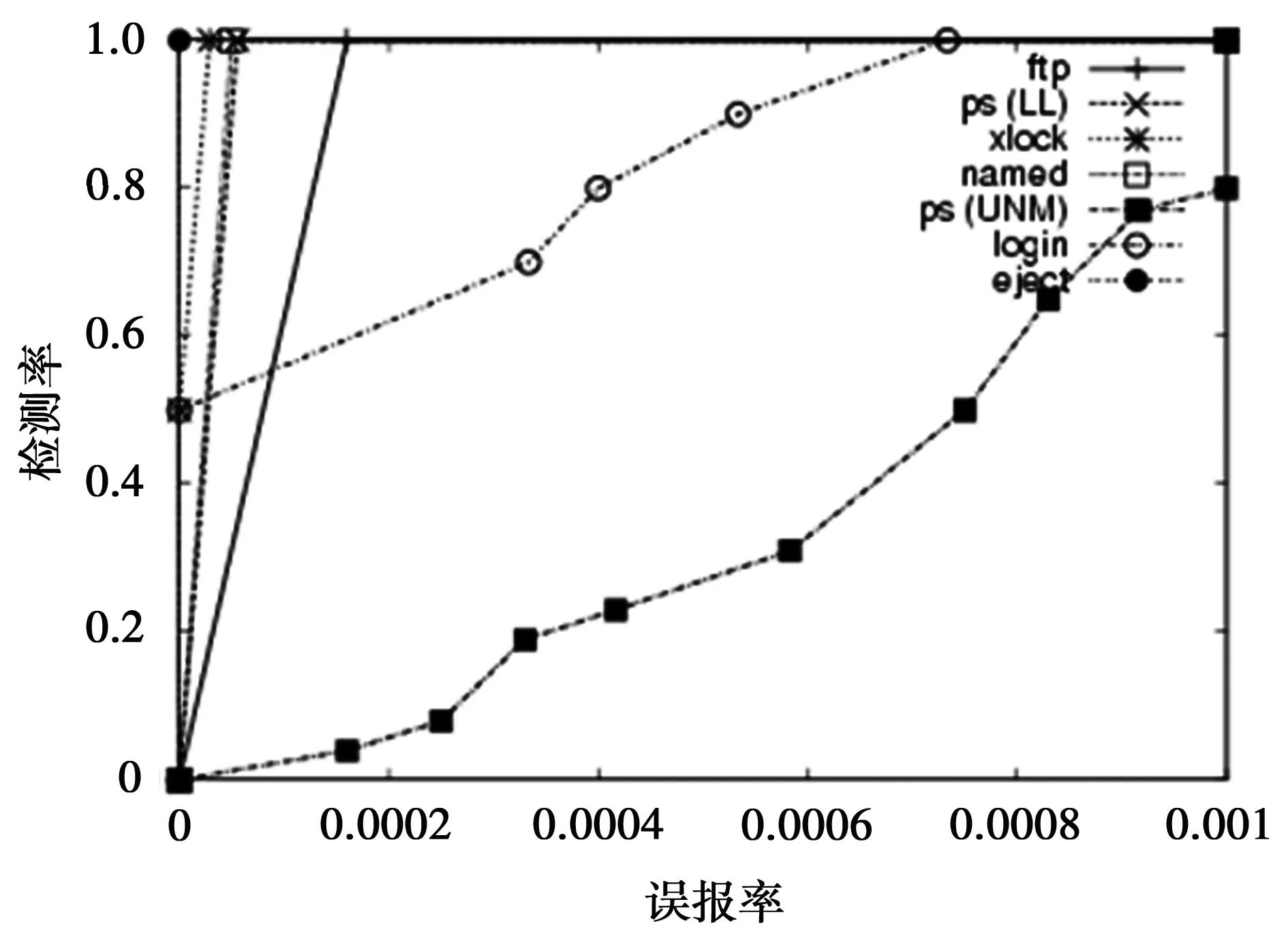
图3 模型对异常数据不同比例的数据集检测效果比较
4 总 结
本文提出了一种只需“混合数据集”的基于概率分布的异常检测模型训练方法。评估了此方法的检测效果,并将其与其他两个传统的异常检测模型训练方法的检测效果进行了比较。实验结果显示,本文的方法又有较好的检测效果,令人满意。

