不确定环境下的致命冲击模型

刘 颖，刘冬雪，马 瑶

(天津科技大学计算机科学与信息工程学院，天津 300457)

冲击模型是可靠性数学理论中的主要研究内容之一，其研究的中心问题是系统失效时间或系统寿命[1]．它在交通[2]、保险[3]、维修[4]、自然保护[5]等领域有着广泛的应用．例如，在飞机设计和验证定理过程中，冲击模型可用于预测飞机结构件的疲劳寿命和可靠性；在环境保护领域，冲击模型可用于分析自然保护区的寿命行为和失效规律；在对金属化膜脉冲电容器“自愈”的失效机理进行研究时，选取合适的冲击模型对金属化膜冲击电容器可靠性进行评估；在保险问题上，也可利用冲击模型对保险风险系统进行建模并给出破产概率估计等．

人们对冲击模型的研究已久，如，Esary等[6]在基础过程是齐次Poisson过程的情况下研究了系统的寿命分布，给出了生存函数的IFR、IFRA与NBU等性质．随后 A-Hameed等[7]将基础过程推广至非齐次Poisson过程的情形．Shanthikumar等[8-9]提出了一般冲击模型．Anderson[10]研究冲击之间的时间间隔具有无限期望的一般冲击模型．Gut[11]建立了混合冲击模型．Lam 等[12]研究了可修系统维修问题的冲击模型．马明等[13]主要研究截断δ冲击模型的参数估计问题，利用极大似然估计法得到截断δ冲击模型的参数估计量，并分析了其无偏性．Cha提出并分析了基于广义波利亚新法的新冲击模型[14]．姜培华[15]建立了一类簇生离散冲击模型，每个周期的冲击次数服从独立同分布的二项随机变量，在累积冲击和极端冲击两种情形下，研究了系统寿命的生存函数和平均寿命.

在研究冲击模型的过程中不得不面对各种非确定性因素．随机性是一种客观非确定性，概率论是研究这种非确定性的有效数学工具．但是使用概率论处理工程问题需要满足 3个前提：事件需明确定义；有大量样本存在；样本之间具有概率重复性．当不同时满足以上的条件时，将不能运用概率论解决问题．这时，一些学者开始运用模糊理论处理此类问题．但 Liu[16]提出的货车过桥问题，分析得出模糊变量并不是适合于不确定量建模的工具这一结论，说明模糊理论处理问题同样存在局限性．

2007年，清华大学的刘宝碇教授提出了不确定理论[17]．近年来，不确定理论被广泛应用在不确定微分方程[18]、不确定统计[19]、不确定规划[20]、不确定金融[21]、不确定控制[22]等众多研究领域．本文将不确定理论引入致命冲击模型的研究中，可对样本规模较小的一类问题进行建模和分析，解决使用概率论建模及可靠性分析不精准的问题．

1 不确定理论

刘宝碇教授提出了不确定理论之后，又对该理论进行了细化和补充，下面给出与本文相关的定义和定理[17, 23]．

假设Γ是非空集合，L是Γ上的子集构成的σ-代数，L中的每一个元素Λ称之为事件．那么，为了进一步介绍不确定理论的公理化定义，对每个事件Λ发生的信度指定一个数值M{}Λ，其中信度M需要满足Liu[17]提出的4条公理：

公理1(规范性) 对于全集Γ，有 M{Γ}=1．

公理2(单调性) 对于任意事件，当 Λ1⊂Λ2时有

公理3(自对偶性) 对于任何事件Λ和cΛ，有

公理 4(次可加性) 对于任意可列可数事件列Λ1, Λ2,… ,都有

定义 1 若集函数M满足规范性、单调性、自对偶性和次可加性，则称M是非空集合Γ上的不确定测度．

定义 2 设Γ为非空集合，L是由Γ的子集构成的σ-代数，M是不确定测度，则称三元组(Γ,L, M)为不确定空间．

定义 3 不确定变量ξ定义为从不确定空间(Γ, L, M)到实数集的可测函数，即对任意 Borel集B，集合为一个事件．

定义 4 不确定变量ξ的不确定分布Φ定义为实数集上的函数，对于任意实数x，

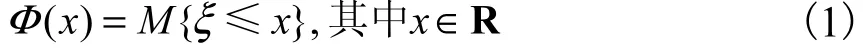
注：由公理3可知

定义5 不确定变量ξ为线性不确定变量，若其不确定分布

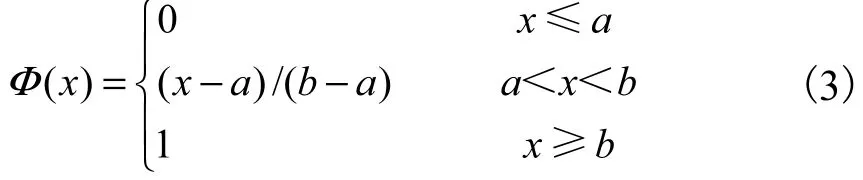
记作L( a, b)，对于任何的实数a和b都有a＜b．

定义 6 设ξ为不确定变量，Φ为其分布函数，那么Φ的反函数Φ-1称为不确定变量ξ的逆分布．

定义 7 线性不确定变量L( a, b)的逆不确定分布为

定义 8 若ξ为不确定变量，M为不确定测度，那么ξ的期望值定义为

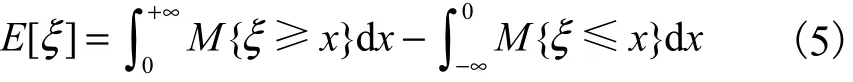
只要以上两个积分中至少有一个是有限的．

定理 1 若不确定变量ξ的不确定分布函数为Φ，且ξ的期望存在，则

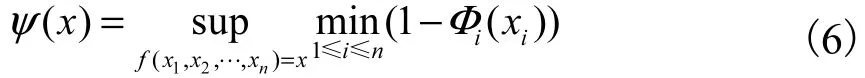
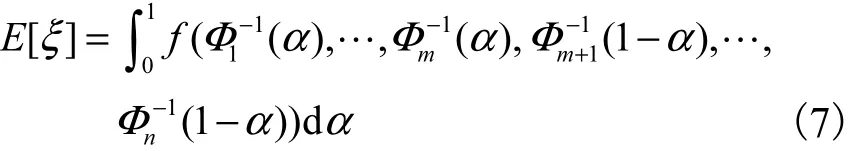
2 建立模型

假设系统由2个部件组成(图1)，这些部件在受到外界冲击后会失效，冲击到达的时间为不确定变量．系统中有3个相互独立的冲击源，当冲击1发生时，仅引起部件 1失效，冲击发生的时间用U1表示，其不确定分布为Φ1(x)；当冲击2发生时，仅引起部件2失效，冲击发生的时间用U2表示，其不确定分布为Φ2(x)；当冲击3发生时，同时引起2个部件失效，冲击发生的时间用U12来表示，其不确定分布为Φ12(x)．因此，可知部件1和部件2的不确定寿命X1和X2分别为

图1 冲击模型Fig. 1 A shock model

定理4 X1与X2的联合生存不确定分布为

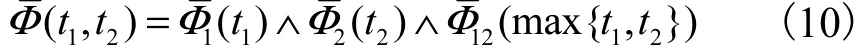
证明：当 0≤t1≤t2时，由式(1)、式(2)、式(8)和式(9)可知

当0≤t2≤t1时，由式(1)、式(2)、式(8)和式(9)可知

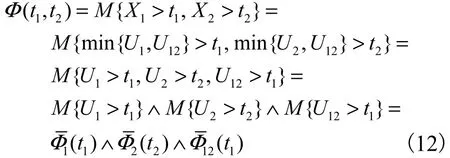
综合式(11)和式(12)，有

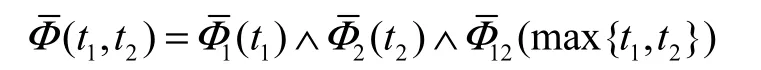
证毕．

定理5 X1和X2的边缘生存不确定分布分别为

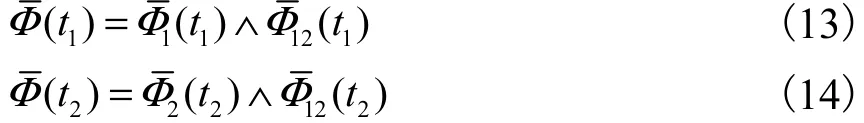
证明：由式(1)、式(2)、式(8)和式(9)可得该致命冲击模型的边缘生存不确定分布分别为

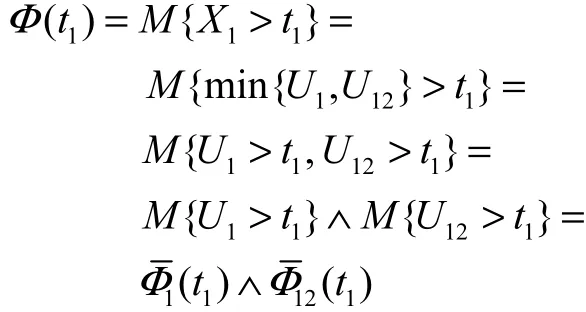
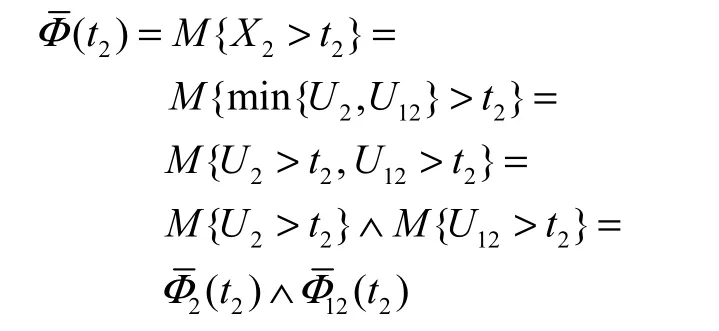
证毕.

定理6 X1和X2的平均寿命分别为

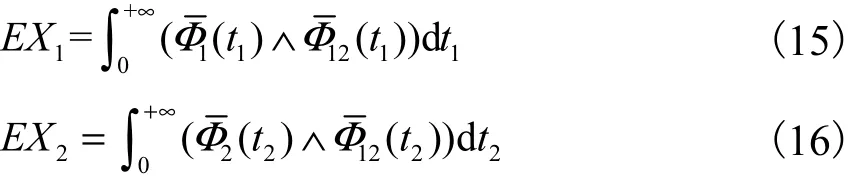
证明：由式(1)、式(2)和式(5)可得

证毕．

定理7 若X1和X2为不确定寿命，则有

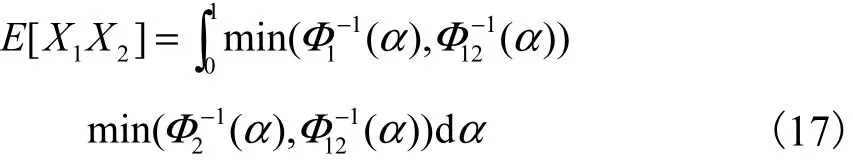
证明：由式(7)、式(8)和式(9)可得

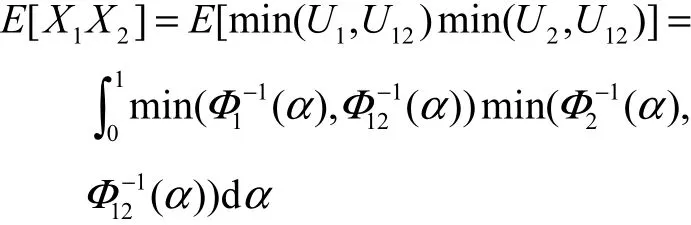
证毕．

定理8 若X1和X2为不确定寿命，则有

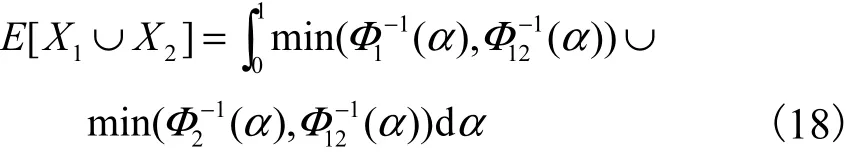
证明：由式(7)、式(8)和式(9)可得

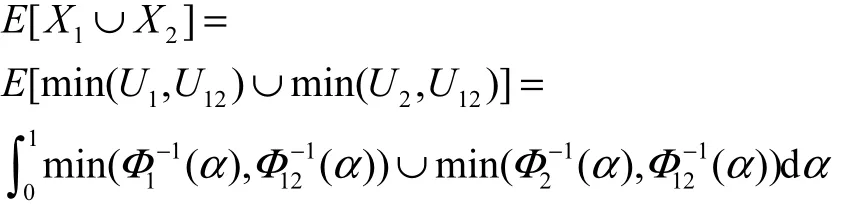
证毕．

定理9 X1和X2的矩母函数为

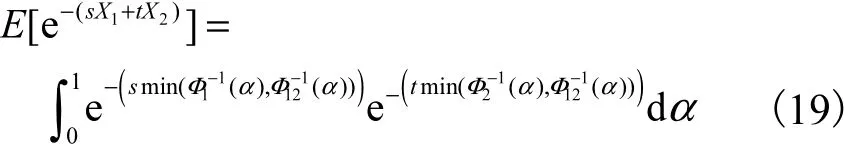
证明：由式(7)、式(8)和式(9)，可得 X1和 X2的矩母函数为

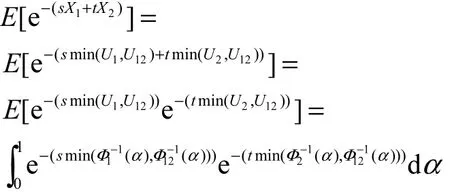
证毕．

3 算 例

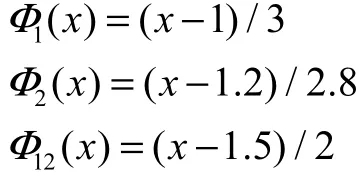
由式(4)可知其逆不确定分布函数分别为

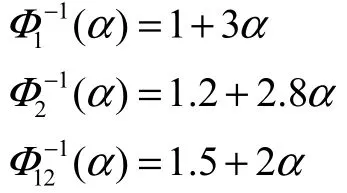
由定理4可求X1与X2的联合不确定分布

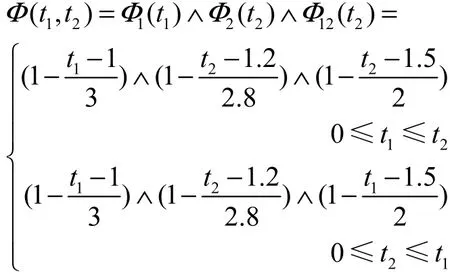
由定理5可得 X1, X2的边缘生存不确定分布为

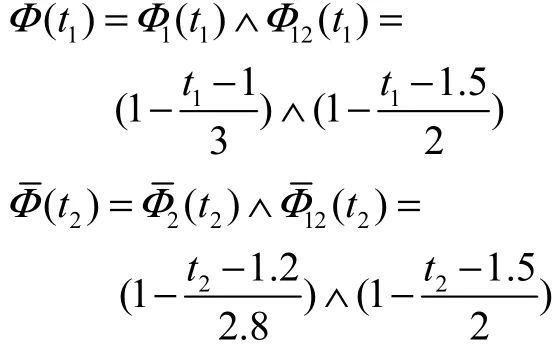
由定理6可知，各部件寿命分别为

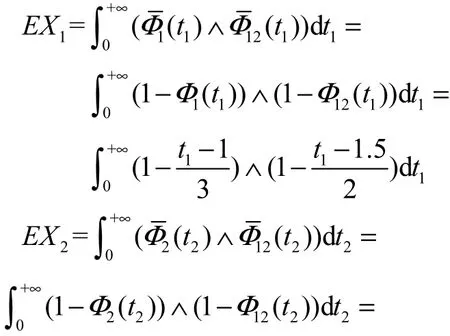
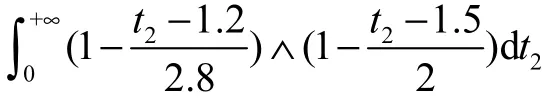
由定理7，有

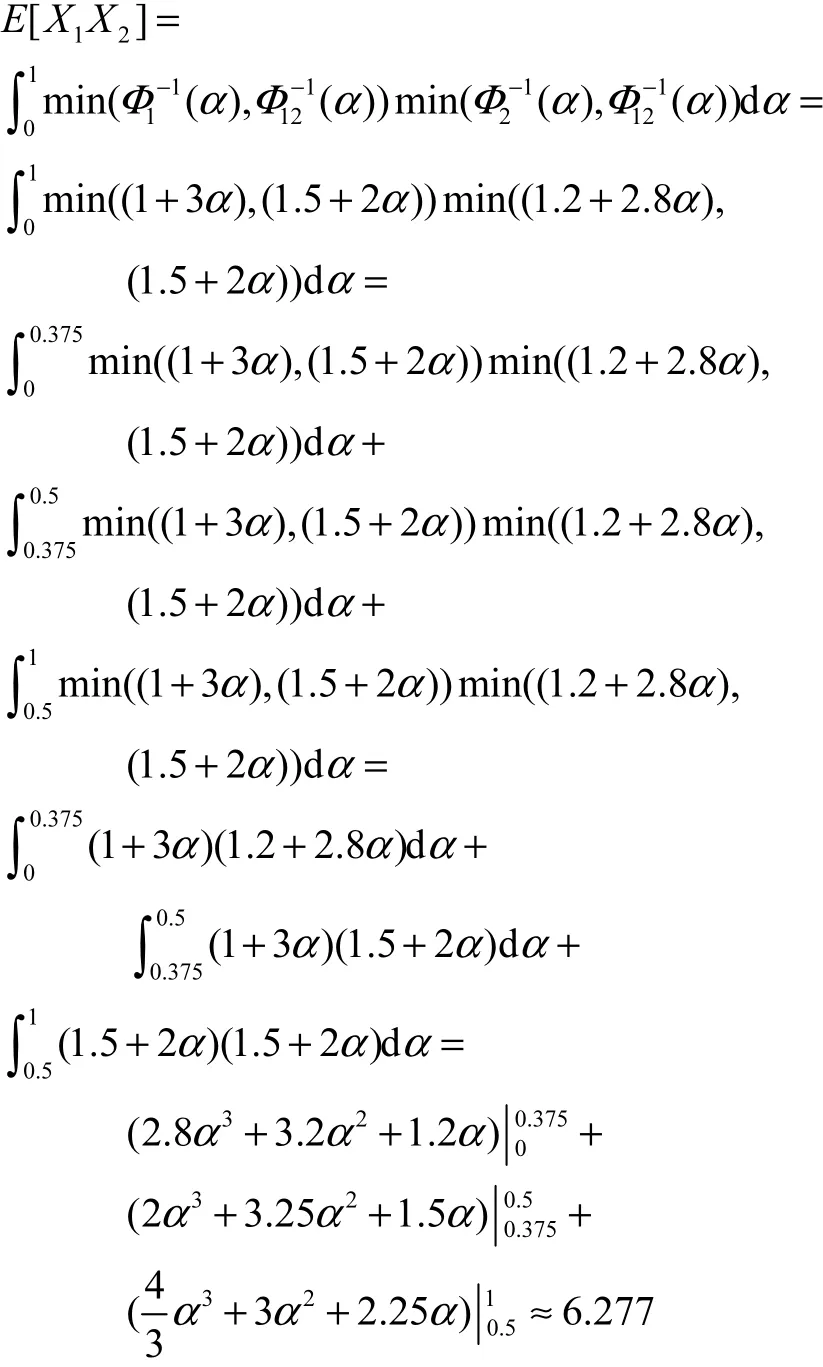
由定理8，有

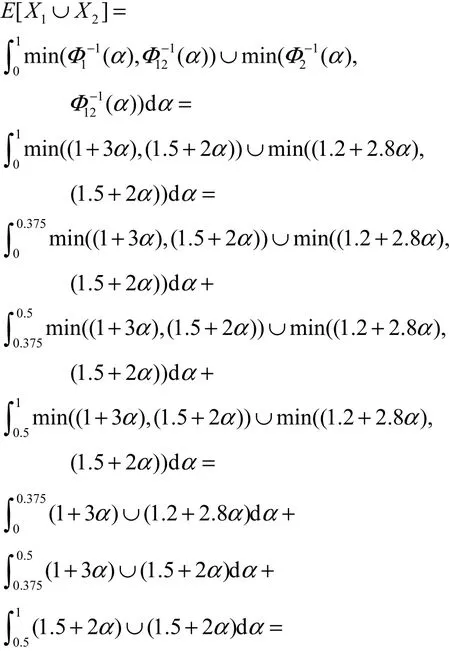
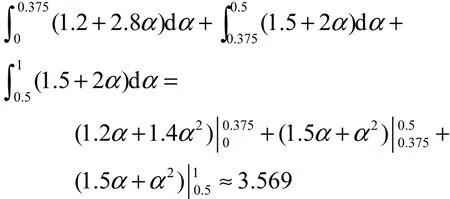
由定理9可得，X1,X2的矩母函数为

4 结 语

不确定理论是建立在规范性、自对偶性、次可加性和乘积测度公理化体系之上的数学分支．当样本规模较小时，概率论将不再有效，此时，采用不确定理论可解决此类问题．本文研究不确定环境下的致命冲击模型，将冲击源引起部件失效的时间视作不确定变量，进行建模和分析，给出了冲击模型的联合生存不确定分布及相关定理．为计算简便，给出了不确定变量服从线性分布时的数值算例，但该方法同样适用于任意不确定分布．

致谢：本文研究得到“2018年中国轻工业重点实验室开放课题(KFKT2018C09)”的资助，特此致谢！