要素流动对效率提升的溢出红利研究

郭兆颖

（1.哈尔滨商业大学 会计学院，哈尔滨 150028；2.哈尔滨金融学院 资产处，哈尔滨 150030）

0 引言

党的十九大报告中明确提到，我国正处在转变发展方式、优化经济结构、转换增长动力的攻关期。在这一关键时期，要以供给侧结构性改革为主线，推动经济发展质量、效率和动力三大变革，提高全要素生产率，加快经济转型升级，加速高质量发展的步伐。站在新的历史时期，如何提升发展效率，是必须面对的重要任务。

经济发展效率方面的研究也是经济领域的一个重点分支，其中有大量的学者对经济发展效率进行测算。Fare等（1994）[1]提出了一种Malmquist模型，为测算全要素生产率提供了一种有效模型方法，从而为经济发展效率的研究提供了一种新的工具。RestuccIA和Rogerson（2008）[2]采用一个增长模型版本，通过测算全要素生产率（TFP），研究了美国的经济发展效率。陈伟等（2017）[3]在借鉴Malmquist模型方法的基础上，通过DEA与Malmquist的结合，选取高新技术产业这一视角，研究了我国省际产业创新效率。

一个地区经济发展效率的提升，是由众多因素的变化共同决定的。其中，要素的流动改变了区域间、行业间的资源配置，对一个地区或产业效率的提升带来重要辐射力[4]。Brandt等（2013）[5]通过实证研究发现，劳动力和资本要素的配置扭曲，将明显削弱区域的全要素生产率。王晓芳和胡冰（2016）[6]采用一种变异系数方法研究发现，区域间要素的差异化会对区域间经济增长的差异化带来重要影响。孙英杰和林春（2018）[7]通过系统矩估计实证分析发现，科技进步对我国经济全要素生产率具有关键性作用，进一步论证了技术要素在效率提升上的重要性。可以说，要素流动对效率提升而言是一种溢出的红利。但遗憾的是，目前国内仍鲜有学者能较为全面地研究要素流动对效率提升的影响效应。基于此，本文在借鉴已有全要素生产率方法的基础上，测算我国的经济发展效率，然后充分考虑劳动力、资本、技术等多重要素，研究要素流动对效率提升的溢出红利。特别地，在实证过程中，考虑到了效率提升可能存在的时滞溢出效应和空间溢出效应，这样可以在一定程度上解决普通计量模型在技术上的局限性。

1 理论模型及测算结果

1.1 测算模型

全要素生产率，是研究经济发展效率的重要指标。本文选择全要素生产率分析方法，借鉴Fare等（1994）[1]的模型方法，测算我国区域经济发展的效率。Malmquist指数表示如下：

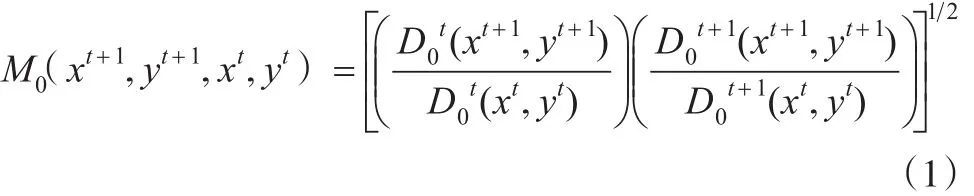
其中，M（0xt+1，yt+1，xt，y）t表示一个经济主体从t期到t+1期过程中的经济发展效率变化。x和y分别为投入要素和产出。D0表示产出距离函数，可由DEA模型求解得到。

可以将Malmquist指数模型作几层分解：

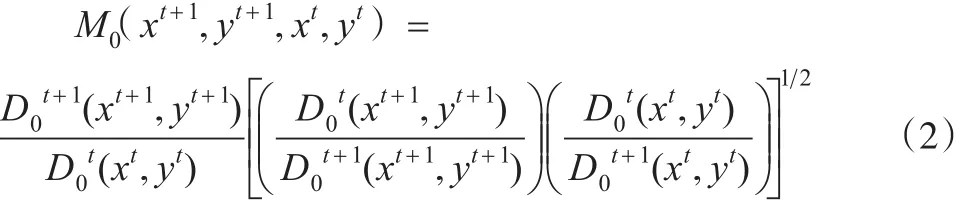
其中，分解式的左半部分为技术效率指数，右半部分技术进步指数，分别记为TE和TM。还可将技术效率指数分解：

其中，TEP0是纯技术效率指数，TES0是规模效率指数，D0（txt，yt|V）代表可变规模距离函数。

1.2 数据样本

本文选取2005—2017年中国大陆30个省级单位（不包括西藏自治区）的数据进行测算。

1.3 结果分析

根据Malmquist指数方法，首先测算2005—2017年30个省级单位各自的纯技术效率、规模效率和技术进步指数，然后对这三个指数分别按照地区取平均值，得到历年三个指数的平均值。最后，根据式（2）和式（3），得到历年全要素生产率的地区均值。结果如表1所示。

表1 2005—2017年我国经济发展效率总体测算结果

由表1可以发现，2005年以来我国的经济发展效率基本上都略大于1（除2007年以外），但是总体上增长较慢，十几年以来平均仅增长了0.2%。从变化趋势来看，我国的经济发展效率呈现了“三降三涨”，其中2005—2015年波动态势较为明显，2015—2017年虽有所提升，但明显趋稳。从三个分项指数的贡献来看，技术进步指数与全要素生产率指数的变化趋势最为接近，由此可以初步认为我国经济发展效率的提高对技术进步起到了重要的贡献。

2 实证分析

2.1 理论模型

本文采用一种因变量自回归模型进行实证分析，这样可以反映效率的提升是否存在动态内生作用性。与此同时，加入空间因素，这样也能考察地理空间溢出性带来的影响。动态空间模型的理论框架如下：

其中，TFPit表示i地区t期的经济发展效率效率水平；X表示反映要素流动的变量体系，包括劳动力、资本和技术三类要素，Y表示控制变量体系；α0为常数项，α1为因变量滞后项的系数值，β和γ为系数组；W为空间相关性矩阵，λ表示空间依赖性系数；ε为带有空间关联性的随机误差项，μ为服从正态分布的随机误差项。

2.2 变量选取

2.2.1 被解释变量

效率提升变量（TFP）。即采用全要素生产率来衡量效率提升，全要素生产率在上文测算得到。

2.2.2 要素流动变量

要素流动，可以在一定程度上提高要素配置的效率，产生溢出红利，从而推动生产效率提升。为了检验这一论断在我国是否成立，对要素流动的变量进行细化：

（1）劳动力要素流动（LM）。从我国劳动力流动的基本现状来看，主要倾向于第一产业劳动力向第二三产业流动。本文采用行业间劳动力流动的一种模型来测算劳动力要素流动情况，公式如下：

其中，LM表示劳动力要素流动，L表示二三产业的劳动力就业总人数，r表示当期的就业增长率，i和t分别表示地区和时期。就业增长率r采用本地当期就业人数净增量与上一期期末就业人数的比值表示。由该模型可以看出，若LM值大于零，那么就表明劳动力要素存在流动，而若LM值等于零，即二三产业就业增长率与该地区就业的总体增长率相同时，就不存在劳动力流动，若LM值小于零，则为劳动力流出。

（2）资本要素流动（CM）。借鉴张辽（2013）[8]等学者的研究经验，本文采用以下模型衡量：

其中，Kit表示i地区t时期资本存量，Kt表示全国该时期的资本存量。若CM大于零，则表明资本要素流入，小于零则为资本流出。

（3）技术流动（TM）。对于技术流动，目前学术界研究相对较少，同时统计数据上也没有非常确切的数据支撑。对此，本文基于统计数据的可得性，采用本地当期发明专利申请量增长率和发明专利授权量增长率的平均值，衡量本地的技术流动。

2.2.3 其他变量

（1）经济发展水平（ECONOMY）。一般而言，一个地区经济越发达，则越能吸引要素流动和集聚资源，为生产效率的提升带来动力。因此，有必要引入经济发展水平的变量。按照惯用的方法，采用地区人均GDP来衡量经济发展水平。

（2）城镇化水平（URBAN）。一个地区的城镇化水平越高，则功能配套设施越完善，一般也就越能吸引高端资源、人才入驻，于是对该地区的生产效率提升具有重要的促进作用。因此，有必要引入城镇化水平变量。本文选择一个地区的城镇人口占总人口比重衡量城镇化水平。

（3）人力资本（HCAPITAL）。人力资本体现了劳动者受教育、实践、培训等途径获得的知识和技能的积累，对生产效率的提升具有重要作用，因此也应作为一个重要的影响因素变量。本文采用地区教育经费支出额表示。

（4）政府支持力度（GOV）。受传统体制影响，我国技术创新发展带有一定的政府主导性，一些地方政府为扶持科技型企业或项目落地发展，往往会给予一定的财政补贴。可以说，政府补助在一定程度上会刺激研发。但另一方面，过度的政府支持，会给创新披上“保暖衣”，事实上会削弱竞争力。究竟政府支持对生产效率提升带来促进还是阻碍作用，有待考证。本文选取地方政府财政支出额占GDP比重衡量政府支持力度。

（5）外资水平（FOREIGN）。外资很可能伴随先进的技术和管理理念，对本地的技术进步起到一定的促进作用。但外资的过度引入，也会导致过度地占领本地市场，反而不利于本地技术创新。因此究竟外资对生产效率提升带来何种影响，也有待考证。本文选取外商直接投资额衡量外资水平。

除此之外，产业集聚水平、市场化水平、信息化水平等因素也会影响效率提升，但考虑到变量的增多会产生更大的自相关性，影响模型回归效果，同时也考虑到这些变量的指标衡量存在数据获取制约，因而本文不再引入。

2.3 数据样本

对于以上变量指标，本文仍选取2005—2017年30个省级单位的面板数据进行实证。2005—2016年的指标数据来源于国家统计局网站、各地方统计年鉴和中经网数据库。2017年的数据则通过各地方统计年鉴、中经网数据库和国研网数据库搜寻得到。为确保数据平稳性，对经济发展水平、人力资本、外商直接投资额三个量值较大的变量进行对数处理。

对于空间权重矩阵W，采用“0-1”法进行赋值。具体地，如果两个地区i和j之间相邻，那么wij赋值为1，如果i和j不相邻，那么wij赋值为0。特别地，为消除海南省的孤岛性，假设它与广东省相邻。

2.4 结果分析

2.4.1 变量描述性统计

各变量的描述性统计如表2所示。

表2 变量的描述性统计

2.4.2 空间自相关性分析

根据莫兰指数方法，测算空间自相关性指数，观察空间自相关性。莫兰指数公式如下：

其中，Moran’s I为空间自相关指数值，n表示地区数量，Yi表示第i地区的相关指标值，Yj表示第j地区同一指标数值，Y*表示该指标的区域平均值，wij表示标准化空间权重矩阵W的元素值。

经测算，绘制2005—2017年经济发展效率的空间自相关性变化趋势，如图1所示。可以发现，近十几年来我国经济发展效率的空间自相关指数变化总体稳定，基本维持在0.3上下，说明经济发展效率在区域间可能存在空间关联效应。

图1 空间莫兰指数变化趋势

2.4.3 实证结果分析

采用Matlab的空间计量模型库进行计算，结果如表3所示。

表3 回归结果

从空间回归结果来看，空间权重矩阵所在变量的系数值λ均为正，且均通过1%的显著性检验，即强烈拒绝了影响不显著的零假设。因此，地区之间效率提升的空间溢出效应是比较明显的，即一个地区经济发展效率的提升，会通过空间溢出效应，带动周边地区效率提升。也就是说，我国地区经济发展效率正向的空间溢出效应。

从自回归结果来看，因变量滞后项的系数值均为正，且均通过1%的显著性检验。由此可见，一个地区经济发展效率的提升，是带有路径依赖性特征的，即前一年经济发展效率的提升，会通过顺延作用，促进当年经济发展效率的提升。

由三个要素流动的结果可知：

（1）劳动力要素流动（LM）的系数为正，且通过5%的显著性检验。这说明了劳动力要素的流动存在着较强的溢出红利现象，即通过区域间、行业间劳动力要素流动，可以发挥劳动力要素溢出效应，为经济发展效率的提升带来红利。从产业发展角度看，目前经济效率提升的重心仍在于二三产业，农村剩余劳动力向二三产业流动，有利于优化当地的产业结构，加速全社会劳动生产率提升，从而促进区域经济发展效率提高。

（2）资本要素流动（CM）的系数值也为正，且通过10%的显著性检验。由此可以得出，资本要素的流动也能对区域经济发展效率的提升带来溢出红利。从理论上讲，资本要素的流动，可以有效优化配置资本，降低资本要素配置的扭曲性，溢出结构性红利，从而推动生产效率提升。实证结果虽然证实了这一点，但系数值并不高，原因可能是：近年来我国投资规模增长迅速，有大量资本投入到产能过剩的工业行业和房地产等行业，而实际向边际产出效益高的高科技行业的流入相对不多，影响了整体投资效率的提升。

（3）技术流动（TM）的系数值虽然也为正，但并没有显著性检验，这就说明技术的流动并没有给效率提升带来明显的溢出红利。理论上，生产效率增长点的获得，就是需要技术来供给，而实证结果显示技术流动没有明显的正向溢出红利，这似乎为我国创新创业的发展环境有关。从前面全要素生产率的测算结果可以发现，技术进步是影响全要素生产率增长的重要贡献因素。但在现阶段，我国的创新环境仍然不完善，特别是对知识产权保护相关的立法、制度和政策体系不够健全，从而诱使很多技术流动变成技术模仿，无法真正地带动全社会的生产效率提升[8]。

3 结论

基于上述实证研究，结论如下：

（1）近十多年来，我国的经济发展效率总体上处于平稳小幅增长。从动态趋势来看，经济发展效率呈现了“三降三涨”。从分项贡献来看，技术进步对经济发展效率的提升起到了重要的贡献。

（2）劳动力和资本两类要素的流动，都存在着溢出红利，促进经济发展效率提升。相比之下，劳动力要素对效率提升的溢出红利更为明显，而资本要素主要由于更多地流向产能过剩的工业行业和房地产等行业而较少流向高技术行业，因而在资本配套效率上难以发挥应有作用，进而对效率提升的溢出红利相对较低。

（3）受我国创新环境不够理想、技术流动更多地诱使技术模仿的影响，技术流动并没有为效率提升带来明显的溢出红利。