不确定执行时间的云计算资源调度

李成严　曹克翰　冯世祥　孙巍

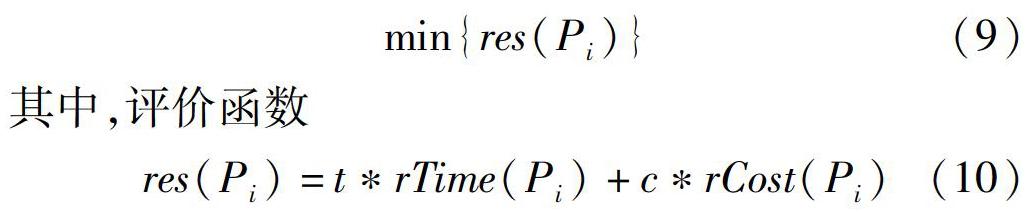
摘要：针对执行时间不确定情况下的云计算资源调度问题，基于模糊规划理论建立了时间-成本约束条件下的模糊云资源调度模型，使用三角模糊数表示不确定的任务执行时间，以最小化评价函数的平均值和不确定度作为调度目标。提出一种改进的混沌蚁群算法对模型进行求解，算法引入精英策略优化了信息素的更新，采用折叠次数无穷大的混沌映射进行混沌搜索，并设计了自适应混沌扰动机制以增强算法的全局搜索能力。在Cloudsim平台上用仿真数值实例对模型和算法进行验证，证明了模型的可靠性，实验结果表明改进算法在收敛速度、求解能力和负载均衡上均有较好的性能。

关键词：

云计算;资源调度;模糊规划;混沌扰动

DOI：10.15938/j.jhust.2019.01.014

中图分类号： TP399

文献标志码： A

文章编号： 1007-2683（2019）01-0085-07

Resource Scheduling with Uncertain Execution Time in Cloud Computing

LI Cheng yan，CAO Ke han，FENG Shi xiang，SUN Wei

（School of Computer Science and Technology， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：For the problem of cloud computing resource scheduling， based on the fuzzy programming theory， a fuzzy cloud resource scheduling model under time cost constraint was set up， the uncertain execution time of tasks is represented by the triangular fuzzy number， and the target is to minimize the average value and standard deviation of the evaluation function An improved chaotic ant colony algorithm was proposed to solve the model， the elitist strategy is introduced to optimize the pheromone updating， a chaotic mapping with infinite folding times is used for chaotic search， and the adaptive chaotic disturbance mechanism is designed to enhance the global searching ability The model and algorithm were tested on the Cloudsim platform， the reliability of the model was proved， and the experimental results showed that the proposed algorithm had better performance in convergence speed， solution ability and load balance

Keywords：cloud computing; resource scheduling; fuzzy programming; chaotic disturbance

0引言

云计算系统应用虚拟化技术，以较低的成本提供高质量的资源服务，用户根据自身需求选择并付费使用相应的服务[1]。云计算资源调度的研究目标是合理的将多个任务分配到虚拟资源节点上执行，并满足执行时间短、所需成本低、虚拟资源集群负载均衡等条件，文[2]证明了该调度问题是一个NP完全问题。

当前云计算资源调度问题的研究主要集中于确定环境下，文[3]提出了云计算任务调度中一种基于权重的混合启发式方法。文[4]以最小化完工时间为目标，建立了云计算任务调度模型。文[5]建立了云计算环境下的多目标工作流调度模型，在降低完工时间和成本的同时，减少能耗。在以上这些研究中，均假设任务在虚拟机上的执行时间是已知的确定值，然而在实际系统中，任务在完成之前其执行时间是不确定的，称为不确定性或异步性，这是由当前的计算机任务执行特性所决定的。因此造成云资源调度的初始条件是不确定的，所以在研究资源调度问题时必须予以考虑。在引入不确定性后，对云计算资源调度问题的求解变得更加复杂，对不确定量的描述有随机变量、模糊变量、灰色变量等，模糊变量是在当概念的外延不清晰时使用的一种方法。在资源调度问题中，任务的执行时间存在不清晰的特征，因此模糊变量和模糊优化技术是一种有效的手段。文[6]研究了云计算中基于模糊的资源重调度问题，文[7]建立了以最小化作业完成时间为目标的模糊调度模型。本文使用三角模糊数表示不确定的任务执行时间，建立了模糊云资源调度问题的期望值模型。

为求解云计算资源调度问题，智能优化算法得到了较多的应用，如遗传算法[8]（GA）、粒子群算法[9]（PSO）和蚁群算法[10]（ACO），但以上算法皆有不足，因此国内外学者对它们进行了改进。文[11]在PSO中引入了贪心算法，通过贪心算法快速求解PSO的初始粒子值。文[12]将混沌系统和蚁群算法结合起来，提出了一种混沌蚁群算法（Chaotic Ant Colony Optimization Algorithm，CACO），通過混沌扰动使算法跳出局部极值区间。文[13]在蚁群系统中使用了精英策略，加快了算法收敛速度的同时提高了解的质量。为进一步优化算法的性能，本文在CACO的基础上，引入精英策略，并设计了自适应混沌扰动机制，提出了一种基于精英策略的改进算法（chaotic ant colony optimization algorithm based on elitist strategy，ECACO）。

本文使用模糊规划的方法，在云计算资源调度问题中引入不确定的任务执行时间，建立模糊云资源调度问题的期望值模型，并提出一种改进算法对模型进行求解。本文结构如下，第1部分建立了模糊云资源调度问题的期望值模型，并对模型的求解进行了分析，第2部分介绍了算法的设计过程，第3部分通过仿真实验对模型和算法进行验证，最后作出结论。

1模糊云资源调度问题

1 1模糊云资源调度模型

云计算中资源调度问题可以描述为将任务集合 T={t 1，t 2，…，t n}中的n个任务，分配到虚拟机集合VM={vm 1，vm 2，…，vm m}中的m个虚拟机上执行（m

RCU={rcu 1，rcu 2，…，rcu m}（1）

ETC= 11 12 … 1n

21 22 … 2n

m1 m2 … mn （2）

其中，rcu i为vm i单位时间内执行任务消耗的资源成本。在一个完整的资源调度方案P中，虚拟机vm i执行任务所需时间vmTime i和成本vmCost i分别为

vmTime i=∑nj=1d j × ij ，d j ∈vmTask i（3）

vmCost i=vmTime i×rcu i（4）

其中，vmTask i为分配在vm i上执行的任务集合。执行调度方案P i需要的总时间为

Time（P i）= max {vmTime 1，vmTime 2，…，vmTime m}（5）

执行任务的总成本为

Cost（P i）=∑mi=1vmCost i（6）

在云环境中，资源的调度需要考虑多方面的因素，任务完成时间决定了客户的满意度，而资源提供商希望尽可能的降低成本，因此提出一个时间-成本约束条件，将两者同时纳入考虑范围。其中，时间约束函数为

rTime（P i）=Time（P i）-Time MIN Time MAX -Time MIN （7）

成本约束函数为

rCost（P i）=Cost（P i）-Cost MIN Cost MAX -Cost MIN （8）

其中，Time MAX 、Time MIN 为任务在性能最差、最好的机器上运行所需要的时间，Cost MAX 、Cost MIN 为任务在执行时所需的最高、最低成本。rTime（P i）和rCost（P i）的值越小，执行任务所需的时间和成本就越少。

在时间-成本选择约束条件下的云计算资源调度模型为

min {res（P i）}（9）

其中，评价函数

res（P i）=trTime（P i）+crCost（P i）（10）

由于任务在虚拟机上的执行时间是模糊数，所以评价函数值也是模糊数。目标函数是使基于时间-成本约束条件的评价函数的期望值最小。其中： t是 时间因子，c是成本因子， 且t+c=1。可以通过调节t和c的取值来影响资源选择时的倾向，当t=1，c=0时，调度的目标为最小化任务完成时间;当t=0，c=1时，调度的目标为最小化成本;当t=0 5，c=0 5时，调度的目标为使任务完成时间较短的同时，令成本也较低。

定义虚拟资源的负载均衡函数为

Load= min 1≤i≤m vmTime i max 1≤i≤m vmTime i（11）

式中， min 1≤i≤m vmTime i表示调度方案中虚拟机的最短执行时间， max 1≤i≤m vmTime i为虚拟机最长执行时间，即调度方案总执行时间。由式（11）可知

1）若 max 1≤i≤m vmTime i=0，则任务还未被执行;

2）若Load=0且 max 1≤i≤m vmTime i！=0，此时有空闲虚拟机;

3）若Load=1，则各虚拟机的执行时间相同，此时系统的负载均衡性达到最佳，Load的值越接近1，证明系统对资源的利用越充分。

1 2模型轉换

本文使用三角模糊数来表示任务在虚拟机上不确定的执行时间e～ ij ，三角模糊数R～=（r L，r M，r R）的隶属度函数图如图1所示，其中r L、r M、r R代表了3个端点值。应用三角模糊数建立模糊模型后，在求解模型时需要使用模糊运算。

在对模糊云资源调度模型的求解中，涉及到了模糊加法、模糊乘法和模糊取大三种运算。例如将任务分配到一个虚拟机上执行时，会累积该虚拟机的运行时间和成本，此时需要进行模糊加法运算，计算虚拟机的成本消耗时，会进行模糊乘法运算，而在求解任务总执行时间，即计算式（5）时，需要进行模糊取大运算。文[14]定义了这三种运算。

取任意两个三角模糊数X～、Y～和任意实数λ，对它们执行模糊运算的结果为模糊加法：

X～+Y～=（x L+y L，x M+y M，x R+y R）（12）

模糊乘法：

λ X～ =（λx L，λx M，λx R），λ≥0

（λx R，λx M，λx L），λ<0（13）

模糊取大：

X～∨Y～=（x L∨y L，x M∨y M，x R∨y R）（14）

记Z～=res（P i），因模糊运算具有可分解性，所以Z～的3个端点Z L，Z M，Z R只和模糊执行时间e～ ij 的3个端点e～ ij L，e～ ij M和e～ ij R相关，可按照模型依次求解。则式（9）可转化为

min {res（P i）}= min {Z～}= min {Z L，Z M，Z R}（15）

云计算资源调度问题是一个在众多调度方案中选取最优方案的决策问题，本文的调度目标是最小化评价函数期望值。不同于确定模型中可以直接对确定值排序，模糊数之间的排序较为复杂。文[15]提出了一种较好的三角模糊数排序方法，使用式（16）和（17）计算三角模糊数的平均值和标准差，若一个模糊数具有较高的平均值和较低的标准差，则认为该模糊数排序更高。

p（X～）=14（X L+2X M+X R）（16）

σ p（X～）=180[3（X L） 2+4（X M） 2+3（X R） 2-4X LX M-2X LX R-4X MX R]12 （17）

根据以上方法，可将模糊云资源调度模型转化为时间-成本约束条件下的单目标规划模型，调度的目标转化为最小化评价函数的平均值和标准差，式（9）可进一步转化为

min {res（P i）}= min {Z～}= min {Z L，Z M，Z R}= min {Z η+Z μ}，∈[0，1]（18）

其中：Z η为模糊数Z～的平均值;Z μ為标准差;是对不确定度的加权系数。

2算法设计与分析

2 1精英策略

在蚁群算法中引入精英策略，可以提高算法的局部搜索能力和收敛速度，使蚁群可以在较少的迭代后找到更优的解。但如果精英蚂蚁过多，解元素的差异就会变小，这会直接影响蚂蚁对路径的选择，导致算法停滞。对此，本文基于排序机制提出一种改进策略：在当前循环结束后，根据生成方案的总执行时间，对所有蚂蚁进行排序，选取一部分执行时间较短的蚂蚁作为精英蚂蚁，对它们留下的信息素增量进行一次更新。引入精英策略后，蚁群的信息素更新公式如下：

τ ij （t+1）=（1-ρ）τ ij （t）+ Δ τ ij （19）

Δ τ ij =∑mk=1[ Δ τ k ij ·（1-ρ）+ Δ τ  ij ]， case 1

∑mk=1 Δ τ k ij ，case2

0， otherwise （20）

case 1：k是精英蚂蚁且将t j分配给vm i

case 2：k不是精英蚂蚁且将t j分配给vm i

Δ τ  ij =Time（P ave ）-Time（P k）Time（P ave ）-Time（P ）·QTime（P k）（21）

其中：ρ为信息素挥发系数;τ ij （t）表示在t时刻路径（vm i，t j）上的信息素浓度; Δ τ k ij 表示第k只蚂蚁在本次迭代中留在路径（vm i，t j）上的信息素增量; Δ τ  ij 为精英蚂蚁的信息素增量;Time（P ave ）为当前循环中所有蚂蚁生成方案的平均执行时间。

2 2自适应混沌扰动

混沌系统是指在一个确定性系统中，存在貌似随机的不规则运动，其行为表现为不确定、不可重复和不可预测，称此现象为混沌现象。混沌运动具有随机性、遍历性和对初始条件敏感的特性，利用这些特性，可以优化搜索。Lyapunov指数是用于衡量一个映射混沌性的重要参照，在某种意义上，它可以看作是映射平均折叠次数的一种表示。常用的Logistic映射和Tent映射产生的混沌序列虽然具有较好的混沌性，但它们的映射折叠次数都是有限的。本文采用的是由式（22）定义的无限折叠映射：

x n+1 = sin 2x n，n=0，1，2，…，x 0∈[-1，1]（22）

当迭代初值x 0不为0时，系统处于混沌状态（实际上初值也不可以为不动点，但上式中的不动点皆为超越数，因此不作考虑）。无限折叠映射的 Lyapunov 指数表达式为

λ= lim  n→∞ 1n∑ n-1 i=0 ln |f ′（x i）|

= lim  n→∞ 1n∑ n-1 i=0 ln 2x 2 i cos 2x i（23）

与Logistic映射和Tent映射相比，折叠次数为无穷大的无限折叠映射显然具有更好的混沌性。在混沌搜索过程中，使用无限折叠映射得到的解会更均匀，以此生成的启发式信息质量更高，将可以更好的指导蚁群的搜索。

蚁群算法容易陷入局部最优解，而精英策略的引入一定程度上放大了这个缺点，因此引入混沌搜索和混沌扰动对其进行优化。在算法初始化过程中，使用混沌搜索来达到全局搜索的目的，然后选择较优路径生成启发性信息，以此初始化蚁群信息素矩阵，指引后续搜索。当蚁群经过一定次数的迭代后，搜索到的最优解变化量不大于一个判定量时，认为算法陷入停滞状态，对当前最优解路径上的信息素量进行混沌扰动。设判定蚁群停滞的迭代次数和判定量分别为 γ和δ（δ为一极小常数），当满足|f t-f t+γ |≤δ（f t和f t+γ 为第t次迭代和第t+γ次迭代的最优解）时，蚁群的信息素更新公式调整为

τ ij （t+1）=（1-ρ）τ ij （t）+ Δ τ ij +ωc γ+1 ij （24）

c γ+1 ij =（1-ω）c γ ij +x ij （25）

式中：ω为混沌扰动系数;c γ ij 为蚁群停滞后第γ次迭代的混沌扰动量;x ij 由混沌映射公式迭代得到。蚁群停滞的时间越长，混沌扰动的强度就越大，如果经过长时间的扰动后，最优解依然没有变化，则认为已找到最优解，算法结束。

ECACO算法的流程图如图2所示。

3仿真实验

3 1算法参数设置

为验证本文提出的模型和算法，在云仿真平台Cloudsim上进行仿真实验。因目前没有适合云计算资源调度问题的标准数据集，本文采用文[16]的方法，在区间[50000，150000]和区间[500，1500]内随机生成任务的大小和虚拟机处理速度，以此作为仿真实验的数据。在实验中，要将每一个确定的执行时间 e ij 转化为三角模糊数，其左端点在区间[ξ 1e ij ，e ij ]内随机生成（0<ξ 1<1），右端点在区间[e ij ，ξ 2e ij ]内随机生成（ξ 2>1），在以下实验中令ξ 1=0 9，ξ 2=1 2。 經过多次重复实验得知，ACO、CACO和ECACO都将在300次迭代中收敛，因此设置算法最大迭代次数为300次。对于ECACO，在蚁群陷入停滞状态后，若进行50次混沌扰动后最优解依然不变，则直到算法迭代结束，当前最优解都将保持不变。即可将混沌扰动50次后依然不变的解视为最终解，因此设置最大混沌扰动次数为50次。

加权系数是用来调整调度时对模糊评价函数的平均值和不确定度的侧重，越大，调度对问题的不确定性越重视。的取值应由具体的应用环境来确定，若在网络传输稳定、虚拟机处理速度较慢这种时间代价较高的环境中，不确定性对调度的影响较小，应取较小的值。而在不确定性大的环境中，应取较大的值。在本文的对比实验中，的取值为0 5，虚拟机的数量为8个，算法的主要参数设置如表1所示。

3 2确定模型与模糊模型对比

为了对任务执行时间确定和不确定两种情况下的模型进行比较，在不同任务规模下，使用ECACO算法对两种模型进行求解。在模型侧重方向的选择中，令评价函数中时间的权重和成本的权重相同，以便同时比较时间和成本的变化，因此设置时间因子 t =0 5，成本因子 c =0 5。确定云资源调度模型和模糊云资源调度模型之间的对比结果如图3所示。可以看出，不确定因素的存在提高了评价函数的值，这意味着任务的执行时间和所需成本会增加，因此必须在调度时考虑不确定性因素的影响，否则会导致理论与实际的偏差过大而降低系统的效率。

3 3算法性能對比

在相同参数下，对ACO、CACO和ECACO进行实验，图4、5、6分别为在任务数量为100的情况下，当 t=0 5，c=0 5时，t=1，c=0时，以及t=0，c=1 时算法的迭代过程。可以看出，不管时间因子和成本因子如何取值，当使用ECACO求解模型时，得到的调度方案都能够在时间和成本的最小化上获得更好的结果。图7是任务数量为400， t=0 5，c=0 5 时算法的迭代过程，可以看出，在大规模的任务调度上，ECACO依然表现出了良好的性能。观察3种算法的迭代曲线，可知当蚁群陷入停滞状态后，ECACO的扰动机制可以使蚁群更快的跳出局部极值区间，找到更优解。相比较于CACO，本文提出的ECACO具有更快的收敛速度和更好的全局搜索能力。除此之外，ECACO能够判断出蚁群是否获得稳定最优解，并且在获得稳定解后提前停止迭代，因此在一定程度上减少了算法迭代的时间，提高了系统的整体效率。

当 t=0 5，c=0 5 时，使用3种算法对不同任务规模下的模型进行多次求解，对得到的解取平均值，结果如表2所示，相对差值列为CACO的评价函数值大于ECACO评价函数值的相对平均值。表2表明，无论是小规模的资源调度还是大规模的资源调度，使用ECACO都能够获得更好的解。图8为 t=0 5，c=0 5 时，不同任务规模下3种算法的负载均衡程度对比。可以看出，ECACO的负载均衡程度明显高于ACO和CACO，这证明ECACO对于资源的利用率更高，可以有效避免虚拟机上的工作负载过重。

通过以上实验可知，本文提出的ECACO收敛速度快、最优解搜索能力强，使用ECACO对模糊云资源调度模型进行求解，可以实现任务完成时间更短、成本消耗更低并且虚拟机负载更加均衡的目标，从而提高云计算系统的综合效率。

4结论

本文使用模糊变量表示不确定的任务执行时间，建立了云计算资源调度问题的模糊规划模型，并提出一种改进算法进行求解。ECACO引入了精英策略增强蚁群的局部搜索能力，然后通过无限折叠映射生成启发式信息和混沌扰动量，并优化了混沌扰动机制，让蚁群在停滞后能更快的跳出局部极值区间。实验证明ECACO具有更好的性能，能够进一步提高云计算系统的效率。不确定因素的存在会使任务的执行时间和成本增加，因此在调度时必须考虑。相对于以往研究，本文提出的模型将不确定因素纳入了研究范围，更符合实际环境中的应用。

参 考 文 献：

[1]JULA A， SUNDARARAJAN E， OTHMAN Z. Cloud Computing Service Composition： A Systematic Literature Review[J]. Expert Systems with Applications， 2014， 41（8）： 3809.

[2]RIMAL B P， JUKAN A， KATSAROS D， et al. Architectural Requirements for Cloud Computing Systems： An Enterprise Cloud Approach[J]. Journal of Grid Computing， 2011， 9（1）： 3.

[3]ABDULLAHI M， NGADI M A， ABDULHAMID S M. Symbiotic Organism Search Optimization Based Task Scheduling in Cloud Computing Environment[J]. Future Generation Computer Systems The International Journal of Escience， 2016， 56： 640.

[4]YAO G S， DING Y S， JIN Y C， et al. Endocrine based Coevolutionary Multi swarm for Multi objective Workflow Scheduling in a Cloud System[J]. Soft Computing， 2017， 21（15）： 4309.

[5]KAMALINIA A， GHAFFARI A. Hybrid Task Scheduling Method for Cloud Computing by Genetic and DE Algorithms[J]. Wireless Personal Communications， 2017， 97（4）： 6301.

[6]KIM J， KIM T， PARK M， et al. Fuzzy Based Resource Reallocation Scheduling Model in Cloud Computing[J]. Lecture Notes in Electrical Engineering， 2014， 301： 43.

[7]SHOJAFAR M， JAVANMARDI S， ABOLFAZLI S. FUGE： A Joint Meta heuristic Approach to Cloud Job Scheduling Algorithm Using Fuzzy Theory and a Genetic Method[J]. Cluster Computing The Journal of Networks Software Tools and Applications， 2015， 18（2）： 829.

[8]HASSAN M A， KACEM I， MARTIN S， et al. Genetic Algorithms for Job Scheduling in Cloud Computing[J]. Studies in Informatics & Control， 2015， 24（4）： 387.

[9]SADHASIVAM N， THANGARAJ P. Design of an Improved PSO Algorithm for Workflow Scheduling in Cloud Computing Environment[J]. Intelligent Automation & Soft Computing， 2016，31（8）： 493.

[10]HU X X， ZHOU X W. Improved Ant Colony Algorithm on Scheduling Optimization of Cloud Computing Resources[J]. Applied Mechanics & Materials， 2014， 678： 75.

[11]ZHONG Z F， CHEN K， ZHAI X J， et al. Virtual Machine Based Task Scheduling Algorithm in a Cloud Computing Environment[J]. Tsinghua Science and Technology， 2016， 21（6）： 660.

[12]MA Y， WANG Y. Grid Task Scheduling Based on Chaotic Ant Colony Optimization Algorithm[C]// International Conference on Computer Science and Network Technology. IEEE， 2013： 469.

[13]YOUSEFIKHOSHBAKHT M， DIDEHVAR F， RAHMATI F. An Efficient Solution for the VRP by Using a Hybrid Elite Ant System[J]. International Journal of Computers Communications & Control， 2014， 9（3）： 340.

[14]BENTRCIA T， MOUSS L H， MOUSS N K， et al. Evaluation of Optimality in the Fuzzy Single Machine Scheduling Problem Including Discounted Costs[J]. International Journal of Advanced Manufacturing Technology， 2015， 80（5-8）： 1369.

[15]BALIN S. Non identical Parallel Machine Scheduling with Fuzzy Processing Times Using Genetic Algorithm and Simulation[J]. International Journal of Advanced Manufacturing Technology， 2012， 61（9-12）： 1115.

[16]CALHEIROS R N， RANJAN R， BELOGLAZOV A， et al. CloudSim： A Toolkit for Modeling and Simulation of Cloud Computing Environments and Evaluation of Resource Provisioning Algorithms[J]. Software Practice & Experience， 2010， 41（1）： 23.

[17]PRIYA V， BABU C N K. Moving Average Fuzzy Resource Scheduling for Virtualized Cloud Data Services[J]. Computer Standards & Interfaces， 2016， 50： 251.

[18]羅智勇，朱梓豪，尤波，等.基于串归约的时间约束下工作流精确率优化算法[J].哈尔滨理工大学学报，2018，23（5）：68.

[19]LU D， MA J， SUN C， et al. Credit based Scheme for Security aware and Fairness aware Resource Allocation in Cloud Computing[J]. Science China Information Sciences， 2017， 60（5）： 052103.

[20]赵辉，吕青，丁树业.模糊综合评判在优化电机冷却系统中的应用[J].哈尔滨理工大学学报，2016，21（6）：106.

[21]ZHANG Y， SUN J. Novel Efficient Particle Swarm Optimization Algorithms for Solving QoS demanded Bag of tasks Scheduling Problems with Profit Maximization on Hybrid Clouds[J]. Concurrency and Computation Practice & Experience， 2017， 29（21）： 4249.