退化过程建模及药品货架寿命预测
周真 李翰斌 齐佳 马德仲

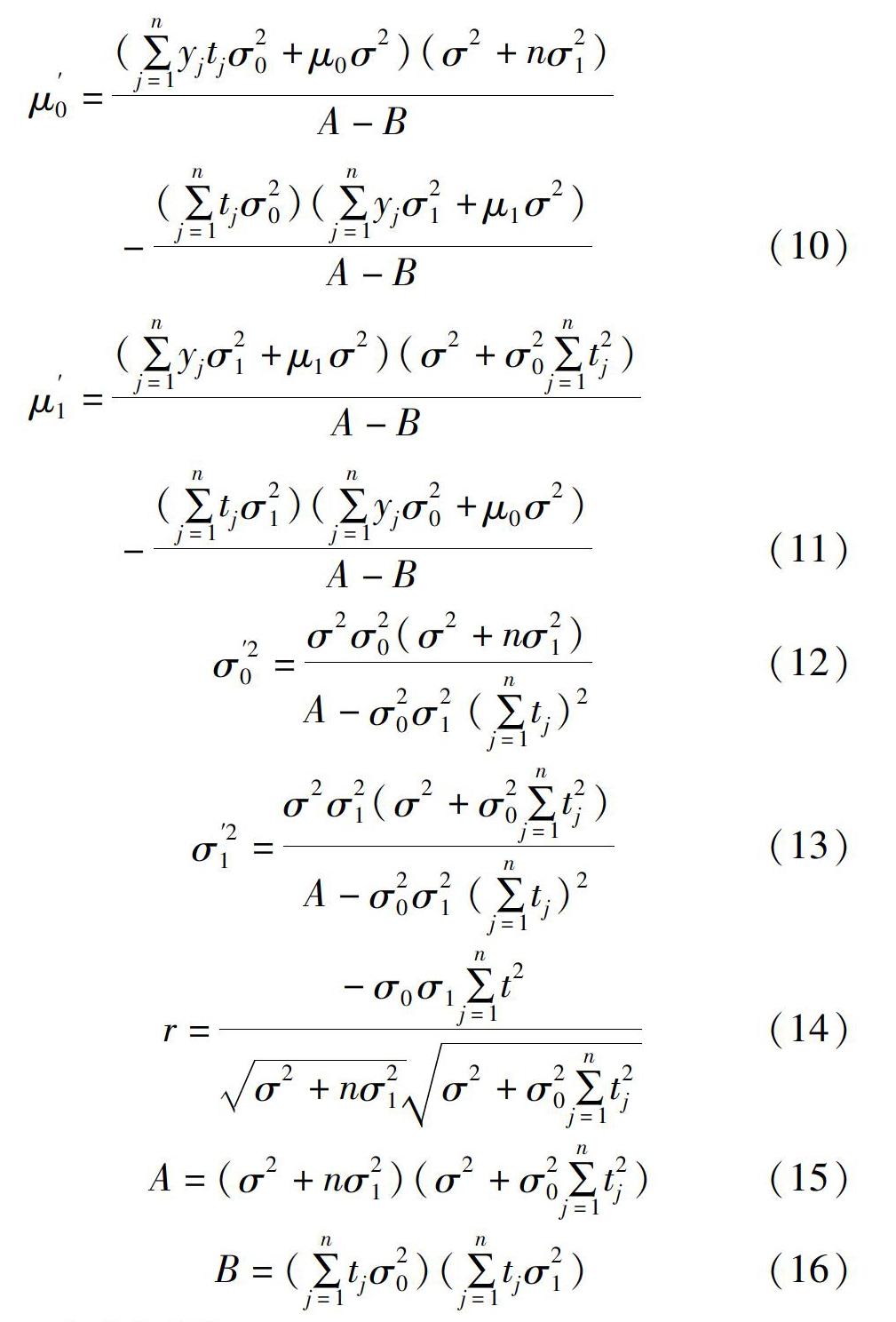

摘要:药品货架寿命的有效预测是药品安全管理的关键问题。针对传统的退化过程建模不能考虑同批产品中个体差异的问题,提出一种有效融合先验退化数据和现场退化数据的方法,可对单片药品及新药品进行货架寿命预测。依据先验信息确定模型的参数,引入Bayes融合现场退化数据进行参数更新,在此基础上对单片药品进行货架寿命预测。结果表明,瓶装和片装的五号药片的货架寿命预测值分别为43 95周和47 47周,与试验值的相对误差分别为0 043和0 051。验证了利用融合现场退化数据对单片药品及新藥品货架寿命预测方法的可行性。
关键词:
退化模型;货架寿命;Bayes理论;药品
DOI:10.15938/j.jhust.2019.01.009
中图分类号: TB114 3
文献标志码: A
文章编号: 1007-2683(2019)01-0055-05
The Degradation Process Modeling and Shelf Life Prediction of Drug
ZHOU Zhen 1,2 ,LI Han bin 1,QI Jia 1,2 ,MA De zhong 1,2
(1 School of Measurement control Technology and Communications Engineering, Harbin University of Science and Technology, Harbin 150080,China;
2 Higher Educational Key Laboratory for Measuring and Control Technology and Instrumentations of Heilongjiang Province, Harbin 150080, China)
Abstract:The shelf life prediction of drug is the key problem of drug safety management. To solve the problem of individual difference in the same batch cannot be considered during the traditional degradation process modeling, an effective method is proposed to fuse priori degenerate data with site degraded data which can predict shelf life for the monolithic drug and new drugs Determining the distribution of model parameters based on prior information, fusion of field data to update parameters by Bayes On this basis, predict the shelf life of the monolithic drug The results show that the No 5 loaded and bottled drugs shelf life predicted values are 43 95 and 47 47 weeks The relative errors are 0 043 and 0 051 And the feasibility of fusing degradation data to predict the shelf life of the monolithic drug and new drugs is verified
Keywords:degradation model; shelf life; bayesian theory; drug
0引言
药品质量和效期问题是比较重大的公共卫生安全问题,它关乎着病人的生命安全。经统计,我国目前药品不良反映案例中,有1/3是由于过期药品引起的。药品过期后将发生内在质量变化,继续使用会引起中毒。比如曾经轰动全国的“梅花K”事件,就是过期变质的四环素导致了患者肾小管功能损害、肝损害等,严重危害用药者健康。用药的最高原则应是“安全、有效”。药品货架寿命是衡量药品安全性和有效性的重要指标,过期的药品对正常药品市场、人民群众身体健康和生命安全都有着严重的影响[1-2]。因此,开展对药品货架寿命的有效预测,为控制和防范药品安全危害,加强药品安全监管提供理论上的支持。
传统的寿命预测方法是基于统计方法得出的共性的平均寿命,难以有效处理小样本少量药剂的失效数据;且缺乏对单个药片寿命预测的准确性[3-4]。实际上,在药品公司研制过程中积累了大量的药品药效退化的信息,利用这些药效退化信息,结合性能可靠性理论与方法,可为药品的货架寿命预测提供一条新的途径[5]。
基于退化轨迹建模及分析理论是解决产品寿命预测等问题的重要手段。近年来,基于退化模型的寿命预测方法研究得到国内外学者广泛关注。Freitas等[6]基于线性退化模型对产品的退化过程进行研究。相比寿命数据,退化数据能够提供更多的可靠性信息。周月阁等[7]基于性能退化和Monte Carlo仿真的可靠性分析方法,阐述了基本的退化建模思想及评估方法,并结合产品的失效数据验证了评估的有效性及正确性。Xu等[8]针对线性性能退化模型,确定参数的先验分布,并对产品中位寿命运用Bayes方法进行统计推断。另外,还有学者对可靠性模型参数的更新进行了研究。Gebraeel等[9-10]与Elwany等[11]研究轴承第二阶段的性能退化轨迹,通过指数模型与不同轴承个体振动幅值的退化趋势相拟合,并利用现场数据对性能退化模型在线更新,预测了轴承的剩余寿命。Kaiser & Gebraeel[12]根据更新后的产品剩余寿命分布对产品进行寿命预测,在此基础上对产品的预防性维修问题进行研究。Chen等[13]提出了一种两阶段的性能退化模型,假定性能退化路径分段线性且分段时间点随机,模型参数的先验分布运用Bayes原理进行更新。尽管已有大量文献基于性能退化数据寿命预测课题进行研究,但仍有问题需进一步解决:①传统方法是对产品总体的寿命预测,而无法体现同批产品个体的差异性。对于高危和昂贵药品,利用已有的退化数据对单片药品进行货架寿命预测更符合药品安全问题的实际需求。②在新产品的研制过程中存在小子样问题,如何对新产品少量药剂进行货架寿命预测,也是所需解决的难题。
针对以上问题,本文在退化数据的基础上对药品药效退化过程进行建模,融合现场退化数据,结合Bayes理论,实现对单片药品及新药品货架寿命预测。最后,通过某种药品货架寿命预测实例验证了本文提出的利用Bayes方法融合现场退化数据对单片药品进行货架寿命预测的合理性。
1退化量统计模型
1 1常用退化轨迹模型
性能退化量是指试验样品在某一工作条件下性能的变化量,它与测量间隔时间之间建立的函数关系为退化轨迹模型。大部分性能退化产品的退化量,可以用以下5种常用的退化轨迹模型进行拟合。在误差允许的范围内,可以将实际的退化轨迹被看作拟合后的退化轨迹[14-15]。
线性函数模型:
y j=ω jt j+λ j(1)
指数函数模型:
y j=λ j exp (ω jt j)(2)
幂函数模型:
y j=λ jt ωj j(3)
对数函数模型:
y j=ω j ln t j+λ j(4)
Lloyd Lipow 模型:
y j=λ j-ω j/t j(5)
式中:j=1, 2,…,n;n为性能退化量的个数;y j为性能退化量;ω j,λ j为待估模型参数;t j为测量间隔时间。
1 2退化量分布法的基本原理
基于统计分析是退化数据分析的主要方法,步骤及实现方法具体如下:
1)性能退化数据(t 1,y 1j ),(t 2,y 1j ),…,(t n,y 1j ) (j=1, 2,…,n)在t 1,t 2,…,t n时刻对n个样品进行测量,失效阈值D f根据相应的国家标准及使用方要求来确定。
2)分析收集到的试验数据,对各时刻所有样本的退化量(y i1 ,y i2 ,…,y im ,i=1,2,…,m)依次分别应用对数正态分布、威布尔分布、正态分布进行假设检验,选择其中最优的分布函数,并求出该分布函数中的待定参数。
3)为了确定最优的退化轨迹模型,运用最小二乘法将步骤2)中所求的分布函数中的参数y j分别与5种常用的退化轨迹模型进行拟合[16]。
2单个产品寿命预测
2 1Bayes原理
根据 Bayes 原理(式(6)),融合未知参数的先验信息和样本信息,得到后验信息,在此基础上对未知参数进行推断。获取单个产品及新品的退化数据x=[x ij ],运用 Bayes 原理对退化模型的参数更新,从而对单个产品及新品寿命预测进行更新。
f(ω,λ|x)=g(x|μ,θ)f(μ)f ′(θ)∫D(μ)∫D(θ)g(x|μ,θ)f(μ)f ′(θ) d μ d θ(6)
其中:f(ω)、f(λ)分别表示ω和λ的先验概率密度函数;f(ω,λ|x)表示后验概率密度函数;D(ω)和D(λ)分别表示ω和λ取值范围;g(x|μ,θ)为似然函数[17]。
2 2线性退化模型参数更新
线性退化建模中参数ω j、λ j的估计是关键,在退化模型分析中,用最小二乘法估计ω j、λ j的值。然而在小样本的情况下这种估计有较大误差,得到的估计结果也不准确,难以用于产品的寿命预测。可以假设ω j服從ω j~N(μ 0,σ 2 0);λ j服从λ j~N(μ 1,σ 2 1)的正态分布且ω j与λ j相互独立。由随机变量的函数分布关系,可得y是服从正态分布的随机变量,记作:
y~N(μ, σ 2)(7)
式中:μ=μ 0t j+μ 1,σ 2=σ 2 0t 2 j+σ 2 1。
假设ω j,λ j的先验分布为正态分布,选取单个试验样本试验,不同试验时间内的试验结果记作:
y=(y(t 1),y(t 2),y(t 3),…,y(t j))。
y的密度函数为:
f(y)=12 π σ e (y j-μ) 22σ 2
则f(y)=12 π (σ 2 0t 2 j+σ 2 1) e (y j-μ 0t j-μ 1) 22(σ 2 0t 2 j+σ 2 1)
似然函數为:
L(Y|ω j,λ j)=∏n j=1 12 π (σ 2 0t 2 j+σ 2 1) e (y j-μ 0t j-μ 1) 22(σ 2 0t 2 j+σ 2 1)
ω j,λ j的密度函数如下:
f (ω j) =12 π σ 0 e - (ω j-μ 0) 22σ 2 0
f (λ j) =12 π σ 1 e - (λ j-μ 1) 22σ 2 1
由 Bayes 公式可得的ω j,λ j后验联合密度函数:
f (ω j,λ j|Y) =f (ω j) f (λ j) L(Y|ω j,λ j)L(Y)(8)
即:
f (ω j,λ j|Y) =f (ω j) f (λ j) L(Y|ω j,λ j) ∫ ω j ∫ λ j f(ω j)f(λ j)L(Y|ω j,λ j) d ω j d λ j
则 ω j,λ j后验联合密度函数:
f (ω j,λ j|Y) ∝f (ω j) f (λ j) L(Y|ω j,λ j)
∝ e - (ω j-μ 0) 22σ 2 0 e - (λ j-μ 1) 22σ 2 1 e -∑n j=1 (y j-ω jt j-λj) 22(σ 2 0t 2 j+σ 2 1) (9)
又因为ω j,λ j的后验分布f (ωj,λj|Y) 是二维正态分布,假设ω j,λ j的相关系数为r,后验分布均值和方差分别为(μ 0′,μ 1′)和(σ 0 ′2 ,σ 1 ′2 ),其概率密度函数如下:
f (ω j,λ j|Y) =12 π σ ′ 0σ ′ 11-r 2 exp -12(1-r 2)
( (ω j-μ 0) 2σ ′2 0-2r(ω j-μ ′ 0)(λ j-μ ′ 0)σ ′ 0σ ′ 1+ (λ j-μ ′ 0) 2σ ′2 1)
其中:
μ ′ 0=(∑n j=1 y jt jσ 2 0+μ 0σ 2)(σ 2+nσ 2 1)A-B
-(∑n j=1 t jσ 2 0)(∑n j=1 y jσ 2 1+μ 1σ 2)A-B(10)
μ ′ 1=(∑n j=1 y jσ 2 1+μ 1σ 2)(σ 2+σ 2 0∑n j=1 t 2 j)A-B
-(∑n j=1 t jσ 2 1)(∑n j=1 y jσ 2 0+μ 0σ 2)A-B(11)
σ ′2 0=σ 2σ 2 0(σ 2+nσ 2 1)A-σ 2 0σ 2 1 (∑n j=1 t j) 2(12)
σ ′2 1=σ 2σ 2 1(σ 2+σ 2 0∑n j=1 t 2 j)A-σ 2 0σ 2 1 (∑n j=1 t j) 2(13)
r=-σ 0σ 1∑n j=1 t 2σ 2+nσ 2 1σ 2+σ 2 0∑n j=1 t 2 j(14)
A=(σ 2+nσ 2 1)(σ 2+σ 2 0∑n j=1 t 2 j)(15)
B=(∑n j=1 t jσ 2 0)(∑n j=1 t jσ 2 1)(16)
2 3寿命预测
结合单个样本信息,确定退化模型参数的后验分布,从而预测单个产品寿命,即估计性能退化参数达到失效阈值D f的时间[18]。
1)性能参数y j≥失效阈值D f
将寿命视为退化轨迹第一次超过阈值D f时对应的时间,通常称为首达时。因此,根据首达的概念,此时对应的寿命T可以定义为T= inf t|y ij (t)≥D f
2)性能参数y j≤失效阈值D f
将寿命视为退化轨迹第一次低于阈值D f时对应的时间,通常称为首达时。因此,根据首达的概念,此时对应的寿命T可以定义为T= inf t|y ij (t)≤D f
3实例应用
药品货架寿命的定义是在生产和包装后,在指定的贮藏条件下能保持其安全性并适用的期限。而药品的保存方式可分为常温保存和冷柜保存[19]。本文选取某种仅适用于常温保存的药品为研究对象,在瓶装和片装两种包装下,分别在不同批药品中进行抽样,瓶装药品和片状药品均随机抽取5片,样品放在货架上(温度10℃~30℃,RH45%~75%,避光),以药效指标作为退化量,当药效指标下降到初始值的10%时判定药品失效,药效指标下降10%所经历的时间,即为该药品的货架寿命[20]。对每个的样品重复测量6次,其中前5次每隔三周测量一次,第6次测量是在第5次测量的6周后测试,测量的退化数据为 y ij (1) 与y ij (2) ,如表1所示。
分别建立药品药效退化模型,将药效退化数据与5种模型(式(1)~式(5))運用最小二乘法拟合,拟合参数如表2所示,且由表2可知瓶装和片装药品药效退化数据与线性退化模型拟合程度最高,均方根误差分别为0 364和0 201。即 y ij =ω j t j +λ j 是瓶装和片装条件下该药品药效最合适的退化模型。
将表1数据和一个新的样品退化数据(见表3)融合。运用Bayes方法更新药品退化轨迹模型参数,按照式(7)~式(16)分别算出更新后退化模型系数 ω j (1) ,λ j (1) 的平均值和方差,ω j (2) ,λ j (2) 的平均值和方差,如表4所示。
监测五号药品失效前的时间为货架寿命实验值。片装和瓶装五号药品的实验货架寿命分别为45 92周和45 17周[20]。二阶Taylor近似估计方法是预测药品货架寿命传统的方法,预测值为同批药品货架寿命的均值,具有参考价值。表5给出本文方法与二阶Taylor近似估计方法对于货架寿命预测的结果。通过与实验值比较可得出预测相对误差,如表6所示。分析可知,二阶Taylor近似估计方法与实验值的差距明显。通过文中方法对五号药品药效退化参数进行更新,药品货架寿命的预测值接近实验值。预测货架寿命精度更高,相对误差更小。
4结语
本文提出一种基于退化数据的药品货架寿命预测方法。通过对药效退化数据的分析,利用Bayes理论融合先验信息和现场退化数据,对药效退化数据和退化轨迹模型进行了更新。实现了对单片药品货架寿命的预测,也可对研发过程中的新药品、昂贵药品的货架寿命预测提供理论指导。该方法摆脱了传统统计方法对大样本统计信息的依赖,实现了对单个产品寿命的预测,为小样本条件下产品寿命的预测提供了有效手段,具有工程应用价值。
参 考 文 献:
[1]胡颖廉 监管和市场:我国药品安全的现状、挑战及对策[J]. 中国卫生政策研究,2013(7):38
[2]林丽花 强化病区高危药品安全管理的效果观察[J]. 中国药物经济学,2016,11(8):191
[3]郭建英,孙永全,于晓洋 可靠性增长技术发展动态诠释[J]. 哈尔滨理工大学学报,2011,16(2):1
[4]朱显辉,师楠,田德文,等 PWM驱动电机可靠性研究发展及展望[J]. 哈尔滨理工大学学报, 2014,19(4):22
[5]胡姚刚,李辉,廖兴林,等 风电轴承性能退化建模及其实时剩余寿命预测[J]. 中国电机工程学报,2016,20(6):1643
[6]FREITAS M A,DE TOLEDO M LG,Colosimo E A Using Degradation Data to Assess Reliability:A Case Study on Train Wheel Degradation[J]. Quality and Reliability Engineering International,2009,25(5):607
[7]周月阁,叶雪荣,翟国富 基于性能退化和Monte Carlo仿真的系统性能可靠性评估[J]. 仪器仪表学报,2014(5):1185
[8]XU A ,TANG Y Objective Bayesian Analysis for Linear Degradationmodels[J]. Communications in Statistics Theory and Methods,2012,41(21):4034
[9]GEBRAEEL N Z,LAWLEY M A,Rong L,Jennifer K Residual Life Distributions from Component Degradation Signals:A Bayesian Approach[J].IIE Transactions, 2005, 37(6): 543
[10]GEBRAEEL N Sesory updated Residual Life Distributions for Components with Exponential Degradation Patterns[J]. IEEE Transactions on Automation Science and Engineering,2006,3(4):382
[11]ELWANY A ,GEBRAEEL N Real time Estimation of Mean Remaining Life Using Sensor based Degradation Models[J].Journal of Manufacturing Science and Engineering,2009,131(5):51
[12]KAISER K A,GEBRAEEL N Z Predictive Maintenance Management Using Sensor Degration Models[J].IEEE Transaction on Systems,Man and Cybernetics,Part A:Systems and Humans,2009,39(4):840
[13]CHEN N ,TSUI K L Condition Monitoring and Remaining Useful Life Prediction Using Degration Signals:Revisited[J]. IIE Transactions,2013,45(9):939
[14]邱榮华, 巨孔亮, 董友耕,等 基于性能退化的小子样电主轴可靠性试验研究[J]. 中国机械工程, 2016, 27(20):2738
[15]晁代宏,马静,陈淑英 应用多元性能退化量评估光纤陀螺贮存的可靠性[J]. 光学精密工程,2011(1):35
[16]蔡忠义, 陈云翔, 张诤敏,等 基于比例失效率退化模型的可靠性评估方法[J]. 系统工程与电子技术, 2015, 37(8):1943
[17]王华伟,高军,吴海桥 基于Bayes模型平均的航空发动机可靠性分析[J]. 航空动力学报,2014(2):305
[18]彭宝华,周经伦,潘正强 Wiener过程性能退化产品可靠性评估的Bayes方法[J]. 系统工程理论与实践, 2010(3): 543
[19]王笑琴 常温保存的药品存放于冷藏处对药效的影响[J]. 医疗装备,2016(18):112
[20]SHAO J and CHOW S C Constructing Release Targets for Drug Products:A Bayesian Decision Theory Approach[J]. Journal of the Royal Statistical Society, 1991,40(3):381

