柱状桥墩顺河桥对山区河道雍水和冲刷的影响研究
,,2,
(1.四川大学水利水电学院,四川成都610041;2.水力学与山区河流开发保护国家重点实验室,四川成都610041)
中国的跨河桥梁工程多以正交为主,但受到地形地质、水文、工程设计等各方因素的制约,部分桥梁无法较好地正交于河道,需设计成斜交形式。当桥轴线与河道的交角等于或接近0°时便为顺河桥,这在山区沿较窄的河道修筑公路时尤为常见,计算顺河桥与河道行洪间的相互影响对工程设计尤为重要。国内外研究桥梁对河道的水力学影响已经较多。从桥梁本身结构分析,有研究认为桥墩布置形式对桥墩绕流及局部流场会产生影响[1];有从水文理论[2]和数学方法[3]等角度来分析。
也有以软件为分析媒介,以垂线平均水流作为研究对象的Mike21模型,模拟计算平面流场及细部的变化情况[4],或者是用河网模型Hec-Ras基于伯努利能量方程以及统一的河道资料来推求建桥前后水面线[5],Hec-Ras是一个拥有一维恒定/非恒定流分析模块的水力模型,主要用于明渠河道流动分析和洪泛平原区域的确定。但是这些研究大都针对平原或丘陵地区跨河桥或交角不大的斜交桥,对山区河道水力学的影响研究不多[6-7]。通过在Hec-Ras模型中设置顺河桥特征参数来探讨顺河桥对山区河道行洪的影响是本文的重点。
1 研究概况
黑水河[8]地处青藏高原东南缘横断山脉中段北端,岷山与邛崃山交汇处,全长122 km,流域面积7 240 km2,水系呈羽状发育。河流穿行于崇山峻岭之中,桥位所在的下游河段河谷较为开阔,河谷多呈“U”型,河底多卵石和漂石,研究区段河道宽30~60 m,河道左岸为具有覆被层的高山陡坡,右岸为村庄。沙坝大桥为右岸顺河桥(G347公路沙坝段水上部分),大桥全长405 m,除上下游的桥台外另有15组×2个圆柱形桥墩,墩高平均约11 m,直径约为1.8 m,每组桥墩平均间距25 m,同一组内的2个桥墩间距4.8 m,另桥梁底板最低高程1 665.47 m。桥跨采用20 m×20 m预应力混凝土简支小箱梁,交角近乎90°,下部结构采用柱式桥墩、桩柱式桥台、钻孔桩基础。大桥设计、校核按100年一遇洪水标准。大桥俯视见图1,一组桥墩的立面形态构造见图2。
2 基于Hec-Ras的顺河桥方案构建
基于Hec-Ras的顺河桥方案构建[9]与跨河桥的不同之处主要在于几何模块的设置,包括概化研究区下垫面和设置顺河桥特征参数两部分。
2.1 概化研究区下垫面
在构建洪水演进模拟方案前需要概化下垫面[10]。根据大桥与所在区的位置关系确定了CS1-CS11共11个水力断面,这些断面的间距是水面线推算的依据[11],其中CS2-CS7区间为顺河桥桥位段。为便于在Hec-Ras中详细分析桥位段中各桥墩附近水力特性,还需要在CS2-CS7间插入若干副断面,见图3。
2.2 设置顺河桥特征参数
设置水系图层后需设置顺河桥特征参数,这也是几何模块的一部分。Hec-Ras模型不具备直接设置顺河桥特征参数的条件,只能通过改变跨河桥特征参数来间接设置。在本研究中,笔者尝试使用“一组桥墩一座桥”的思想,将一座顺河桥“拆分”成对应桥墩组数量的跨河桥。这样做的依据是Hec-Ras模型在进行洪水演进计算中,仅与桥梁模块设置中桥墩的数量、结构、布置等有直接关系,而与整座大桥的形态无关。
沙坝大桥(顺河桥)共有17组桥墩,它们都位于河道的右侧。根据上述思想可将原始顺河桥转换为17座跨河桥,转换后的每座跨河桥都只有1组(2个)桥墩(跨河桥为虚构,因此不必考虑桥梁结构稳定性)。因转换前后桥墩位置形态不改变,固转换后的每座跨河桥的高程要与对应的原始顺河桥墩高保持一致。以一组桥墩为例,转换前后桥墩断面示意见图4。
3 桥梁建设对河道行洪的影响分析
3.1 对河道雍水的影响分析
当所有参数设置完毕后需要进行稳定流分析。Hec-Ras模型将前期输入的各项资料与伯努利能量方程进行耦合,即得到最终结果,以不同频率二维或三维形式的水面线[12-13]示意图展示,见图5。
模型得到的雍水曲线见图6,可知由Hec-Ras模型得到的沙坝大桥总雍水长度约为850 m。
3.1.1雍水长度公式理论推导
为了找寻一个描述顺河桥雍水长度的定量公式,首先给出目前计算跨河桥雍水长度的经验公式(1)和(2):
(1)
(2)
式中L——雍水线性范围内任意两点间的雍水长度,m;ΔH——该两点间的雍水高度差,m;ΔH——以桥墩处为雍水起算点,桥墩上游侧的最大雍水高度,以迭代公式表示;J——河道比降;α——动能校正系数,一般取1.1;ξ——过水面积收缩系数,一般取0.95;B——河宽,m;V——建桥前断面平均流速,m/s;h——建桥前断面平均水深,m;b——桥墩总宽度,m。
显然,顺河桥的雍水长度,等于起始断面单独作用的雍水长度与下游所有断面共同作用的雍水长度之和。为方便表述,最上游起始断面记为第1断面,则其单独作用时的雍水高度(单独雍高,下同)和雍水长度分别为ΔH1、L1,第1断面与第2断面间的距离记为l1,同样地,第i断面处单独雍高和雍水长度分别为ΔHi、Li,第i断面和第(i+1)断面间距记为li,1≤i≤n-1,n为顺河桥桥墩横断面的总数。因此,求顺河桥雍水总长度关键在于求第2到n断面共同作用的雍水长度。
由于最下游桥墩断面处的雍水一定是最小的,因此从第n断面往上游倒推。假设ΔHn已知,则:
(3)
由于受到上游邻近桥墩的阻挡,一小部分雍水在第(n-1)断面处截止,这部分雍水对顺河桥的雍水总长度不产生影响;大部分雍水则穿过第(n-1)断面继续回溯,该部分的雍水长度为(Ln-1-ln-1),此时在第(n-1)断面处上游侧形成一个附加雍高,记为(Ln-1-ln-1)J/2,见图7。
将上述附加雍高与单独雍高ΔHn-1叠加,可得到第(n-1)断面处的实际雍水高度为(Ln-1-ln-1)J/2+ΔHn-1,因此,第(n-1)断面处产生的实际雍水长度为2[(Ln-1-ln-1)J/2+ΔHn-1]/J。
所以有:
Ln-2=2[(Ln-1-ln-1)J/2+ΔHn-1]/J
(4)
需要说明的是,当第i断面计算得到的雍水长度Li-1不大于第i与第(i-1)断面的间距li-1时,则(i-1)断面无附加雍高,只有单独雍高,该断面的雍水长度仅由单独雍高产生;若Li-1不仅大于li-1,同时大于(li-1+li-2),则第i断面产生的雍水不仅影响到第(i-1)断面,还影响到第(i-2)断面,以此类推。
令f为迭代函数,则:
(5)
Li-2=fLi-1
(6)
所以有Ln-3=f(Ln-2),Ln-4=f2(Ln-2),…,L1=f(n-3)(Ln-2),则第2到n断面共同作用的雍水长度为:
L1+L2+…+Ln-1=f(n-3)(Ln-2)+f(n-4)(Ln-2)+
…+f0(Ln-2)+Ln-1
(7)
起始断面单独作用的雍水长度L0为:
(8)
所以顺河桥雍水总长度可表示为:
L=L0+f(n-3)(Ln-2)+f(n-4)(Ln-2)+…+f0(Ln-2)+Ln-1
(9)
由公式(5)—(7)可知两桥墩横端面间距Li的系数为2,因此顺河桥雍水总长度与桥长有如下的关系:
L>l1+l1+l2+…+l1+l2+…+ln-1>2·l1+l2+…+ln-1
(10)
可见顺河桥雍水总长度L与各组桥墩处的雍水高度ΔH都有关系,且大于总桥长的2倍,这一规律是顺河桥桥墩的纵向排布具有对雍水的叠加效应,这种效应是水流自身形态与受桥墩阻扰的流体力学间的能量耦合,在上游段较强而在下游段减弱,直至顺河桥末端消失。
3.1.2合理性分析
以沙坝大桥为例,该桥为15组桥墩的顺河桥。由式(2)可知第15断面的上游侧雍高为0.001 m,J取0.012,每组桥墩间距均为25 m。利用上述推导的理论公式,估算雍水长度,见表1。

表1 根据推导公式计算的沙坝大桥雍水长度 m
根据表1得到的各断面雍水高度,可求得沙坝大桥雍水总长度为831.73 m,接近Hec-Ras模型得到的总雍水长度850 m。将研究区内其他几座桥梁的推导公式计算结果与模型计算结果进行对比,见表2。
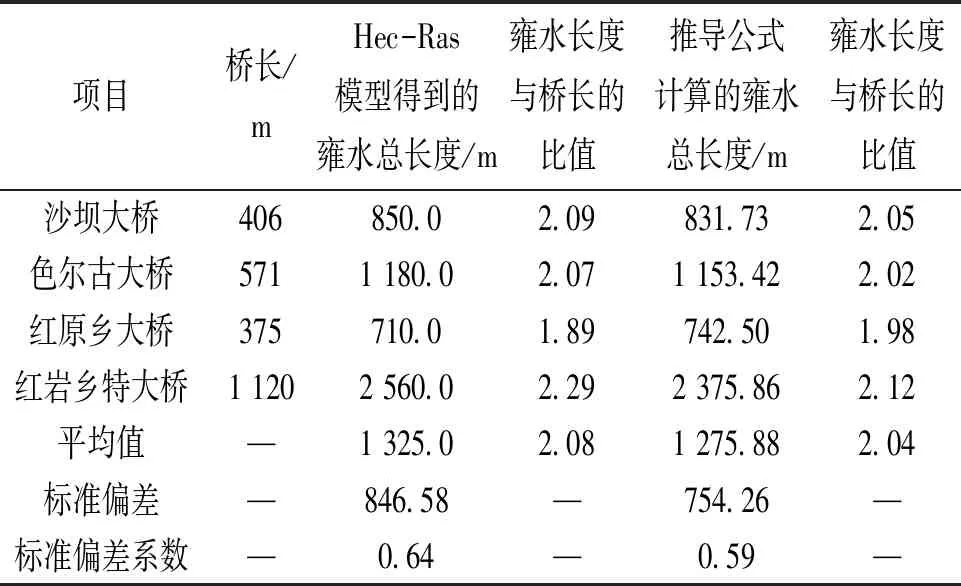
表2 公式计算结果与模型计算结果的对比
可知Hec-Ras模型得到的雍水总长度与推导公式计算的雍水总长度较为接近,且两者的标准偏差系数相差在10%以内,误差较小。因此推导公式的结果可以被认为是合理的。
3.2 对河势稳定的影响分析
顺河桥对河道行洪的影响不仅体现在雍水方面,还影响着河势稳定[14-15]。水力学计算中一般采用根据输沙平衡原理建立的桥下河槽一般冲刷简化式(12)和基于桥墩阻碍水流使水流结构发生变化的局部冲刷式(13)来表示对河势稳定影响的程度。
(11)
式中hp——桥下河槽一般冲刷后最大水深,m;A——单宽流量集中系数,与造床流量下的河槽宽度和平均水深有关;Q槽——建桥后桥下河槽通过的设计流量,m3/s;Qβ——计算断面的天然河槽流量,m3/s;B——天然状态河槽宽度,m;B槽——建桥后桥下断面的河槽宽度,m;λ——设计水位下,桥墩阻水总面积与桥下过水面积比值;μ——桥孔侧向压缩系数;hmax——桥下河槽设计水位对应的最大水深,m。
(12)
式中hb——桥墩局部冲刷坑深度,m;Kξ——墩型系数;B1——桥墩计算宽度,m;h——墩前行近水流深度,以一般冲刷后水深hp代入,m;d——冲刷层内床沙平均粒径,mm;n——指数,与v和v0有关;v——墩前行进流速,以一般冲刷完成时流速计,m/s;v0——床沙起动流速,m/s;v'0——桥墩起冲流速,m/s。
一般冲刷与局部冲刷的简化示意见图8。
根据以上公式分别计算不同设计洪水频率下顺河桥从上游至下游沿程冲刷深度,结果见图9。
从图9可以看出,上游至下游各频率的一般冲刷、局部冲刷现象在各桥墩断面均存在,并呈减小趋势,且一般冲刷变幅大于局部冲刷,黑水河流域其他顺河桥对河势稳定的影响同样存在这一规律。与该地区跨河桥相比,跨河桥对河道的冲刷往往只发生在桥位断面处及其上游临近范围。
这是由于当上游来水时每一组桥墩附近过流面积都会减小导致水沙扰动,进而引起河道冲刷,又因一般冲刷与桥下河槽设计水位的最大水深成正比,从上游至下游雍水高度降低时最大水深逐渐减小,一般冲刷深度也相应减小。另一方面,受桥墩阻碍,部分水流动能转化为势能,由于垂线流速分布不均以及压力分布的上小下大,在和垂线最大流速对应高度稍下处形成一个分界面,界面以上的水流受阻转向水面,引起水位雍高,分界面以下的水流受阻转向河底,形成下降水流。这一系列现象在沿程各组桥墩附近都会发生,由于水流形态的改变以及能量损耗,局部冲刷程度逐渐削弱。
根据以上分析,在实际工程实践中,以顺河桥最下游端桥址为界,至最上游端桥址以上雍水范围内,都应做好桥墩和河道的防护措施,或者通过拓宽河道增大过流面积来降低河势不稳定性。
4 结论与建议
本文以川西高原山区顺河桥对河道的行洪影响为研究对象,构建了一种在Hec-Ras模型中设置顺河桥特征参数的简单方法,从桥梁对河道的雍水和冲刷两方面进行分析,得到以下结论与建议。
a) 山区河道中,顺河桥对河道的影响程度和影响范围比跨河桥更大,并且这种影响与桥梁自身设计有一定的数学关系。
b) 本文仅对柱状桥墩的顺河桥进行分析,无论是对河道雍水的影响,还是对河势稳定的影响,其根本在于顺河桥桥墩的形态及构造。因此针对顺河桥的行洪影响,建议在未来的研究中从不同桥墩形态角度进行分析,从而发现更多水力学规律与桥墩形态结构之间的关系。

