工业专业化集聚对区域流通业效率的动态影响
——基于中国省级面板数据的实证研究
薛虎 朱礼才
(安徽财经大学国际经济贸易学院,安徽蚌埠233030)
一、引言
随着我国现代工业化进程的不断深入,我国的经济形态将逐渐从工业经济向服务经济进行转化,区域工业集聚化和信息化将带动以流通业为首的生产性服务业的发展。目前在关于工业与流通业关系的国外研究中,更多的是把流通业置于生产性服务业框架下,讨论制造业与生产性服务业之间的关系。Francois、Woerz和Macpherson运用需求遵从理论,研究制造业对生产性服务业的影响,发现制造业是生产性服务业发展的基础,生产性服务业依托制造业发展[1][2]。 Preissl、Francois 和 Hoekman 基于产业互动理论,全面研究了制造业与生产性服务业之间的互动关系,发现二者之间是紧密相连、相互促进、共同发展的动态过程[3][4]。 Castellani等学者围绕产业融合理论论述了制造业和生产性服务业通过新技术和新业态的发展,两者之间的价值链不断解构和重组,打破产业界限,实现互补融合[5]。其他相关研究文献也验证了随着工业生产专业化、分工深化和迂回生产程度增加,生产性服务业的中间需求将不断增加,从而推动流通业的协同发展[6][7]。
在国内相关研究中,江小涓、江静、肖文等学者主要从需求遵从以及产业关联互动的视角,剖析得出制造业的发展将不断扩大对生产性服务业的需求,对生产性服务业的发展起促进作用[8]-[10]。李宏使用协整-格兰杰因果检验研究了广东省流通业与制造业的关系,发现广东省制造业发展对流通业的发展起着单向积极促进作用[11]。李晓慧利用投入产出分析法分析了我国流通业与制造业的产业关联,认为工业是流通业中间需求的主要部门,其中制造业占主导地位,且推动了流通业的发展[12]。王文和孙早的实证研究结果表明,这种推动作用存在门槛效应,只有经济水平达到一定的门槛值后,这种推动作用才更大[13]。卫颖认为,制造业的纵向一体化水平越高,其对生产性服务业的需求拉动力越强[14]。唐晓华等学者认为,我国制造业正从增量向存量发展,而流通业等生产性服务业正从存量向增量发展,过快的粗放式发展趋势不利于两者未来的协同发展[15]。
现阶段关于制造业与流通业以及生产性服务业的相关实证研究较多,但只是通过投入产出分析法、灰色关联分析法等方法简单分析二者之间的关联关系,未深入探究二者之间的促进关系。本文从工业集聚的专业化效应出发,使用我国省级面板数据,构建工业集聚的专业化指数指标,探讨工业集聚的专业化效应对流通业全要素生产率的动态影响,通过上述文献综述发现,由于价值链中的互动关系,流通业效率也将影响制造业的发展,因此实证研究中将采用系统GMM模型克服模型的内生性,并根据实证结果,提出相应的政策建议。
二、研究设计
(一)计量模型设定
本文的关注点是工业集聚的专业化效应对区域流通业效率的动态影响。对于流通业效率指标的选取,目前大部分文献采用的是流通业全要素生产率,因此本文也选取这一指标。同时,本文主要探究工业集聚的专业化效应,所以构建区域工业专业化指数。因此,构建工业集聚的专业化效应对区域流通业效率的动态影响的计量模型如下:
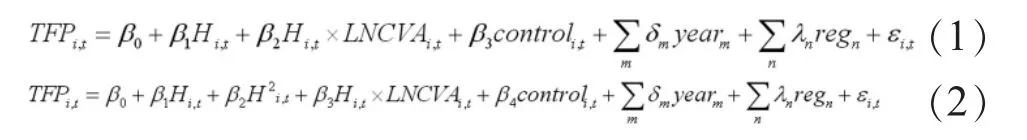
其中,i、t分别代表省份和时间,TFP、H 和 CVA分别为流通业全要素生产率、工业专业化指数、流通业增加值,H2检验工业专业化与流通业全要素生产率之间是否存在“U型”关系,交互项H×LNCVA检验工业专业化对规模不同的流通业全要素生产率的不同影响,control、year、reg 和 ε 分别为控制变量、年份虚拟变量、地区虚拟变量、随机扰动项。
(二)变量选取
1.被解释变量
流通业全要素生产率(TFP)。针对宏观层面的全要素生产率测算方法可以使用包括增长核算法和增长率回归法的非前沿分析方法与包括DEA数据包络分析法和随机前沿分析法的前沿分析方法。本文将使用DEA数据包络分析法中的DEA-Malmquist指数法对流通业全要素生产率进行测算。与其他测算相比,DEA数据包络分析法不需要设定具体的投入产出生产函数形式,避免由于估计函数形式错误而导致偏差,同时,可以研究多投入和多产出的全要素问题[16]。
我国流通业在广义上是指商品所有者一切贸易关系的总和,包含了商流、物流、信息流、资金流,通常是指批发业、零售业、餐饮业、物流业、住宿业、仓储业等产业。由于餐饮业和住宿业属于生活服务业的一部分,我国制定流通业政策时已经很少涉及餐饮业和住宿业,所以本文研究流通业时只选取了批发业、零售业、物流业和仓储业。借鉴胡宗彪、董誉文、柳思维等学者的相关研究[17]-[19],本文的流通业产出采用流通业增加值进行衡量,主要包含批发零售业和交通运输、仓储及邮电通信业。
流通业投入包含劳动投入和资本投入。劳动投入选取各省市分行业年末就业人数中的批发零售业和交通运输、仓储及邮电通信业的年末就业人数总和,但由于部分省份未统计分行业年末就业人数及统计口径不同,本文采用流通业的年末城镇单位就业人数、年末私营企业就业人数和年末个体就业人数的总和作为年末流通业就业人数的代理变量。本投入采用流通业年末资本存量,采用永续盘存法进行估算,公式为:
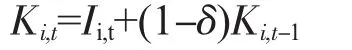
其中,i代表省份,t代表年份,Ki,t和Ki,t-1分别代表i省份在t年和t-1年的流通资本存量,Ii,t代表i省份t年的流通业固定资产投资额,δ代表流通业资本折旧率。基年流通业资本存量采用Kohli方法估算,公式为:
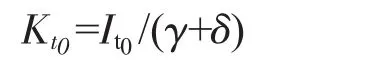
其中,t0为基年,Kt0和It0分别代表基年流通业资本存量和基年流通业固定资产投资额,δ和γ分别代表流通业资本折旧率和观察期内流通业固定资产投资额年均增长率。由于我国法定残值率为3%~5%,且大部分文献选择了5%为折旧率,因此将流通业资本折旧率设为5%。
2.解释变量
工业专业化指数(H)。本文主要研究工业集聚带来的专业化效应,所以构建工业专业化指数指标进行衡量。目前,衡量专业化指数的指标包括赫芬达尔指数、区位熵、基尼系数。本文借鉴苏红键等学者的城市产业专业化指数构建工业专业化指数[20],公式为:
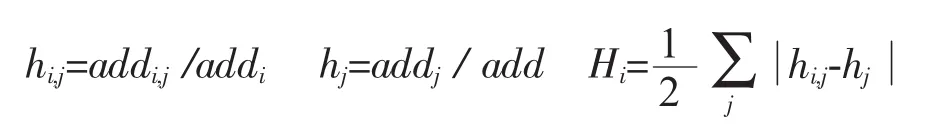
其中,i表示省份,j表示工业中的行业,addi,j和addi分别表示i省份j行业的增加值和i省份的工业增加值,addj和add表示全国的j行业增加值和全国工业增加值,Hi表示i省份的工业专业化指数。Hi的取值范围为 [0,1],Hi越大,区域工业专业化水平越高,即多样化水平越低;同理,Hi越小,区域工业专业化水平越低,即多样化水平越高。
3.控制变量

(三)数据说明
1.数据来源说明
本文基于以省份为观察单元的面板数据样本,探讨分析了2012—2016年间我国30个省市地区工业集聚的专业化效应对其流通业全要素生产率的动态影响。由于制度以及统计口径的差异,未选择香港、澳门和台湾三个地区的样本数据,由于西藏地区的部分统计数据缺失,也把西藏地区从样本中排除。此外,由于各年份《中国工业经济统计年鉴》中的分地区数据中的行业分类不同,所以选择了2012—2016年41个行业进行测算工业专业化指数,除此以外,本文中其他数据均来源于《中国统计年鉴》及各省统计年鉴。
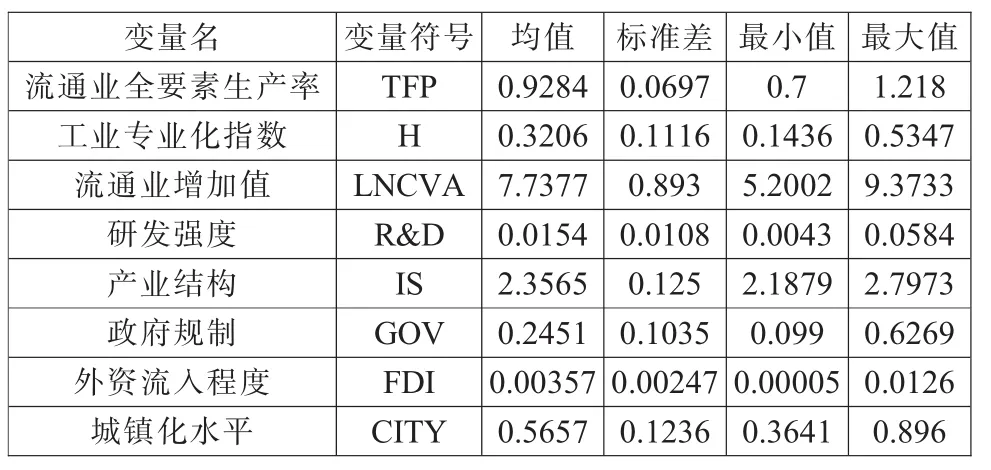
表1 主要变量的描述性统计分析
2.数据描述分析
根据上文收集到的数据,对计量模型中的主要变量数据进行了简单的统计性描述分析 (见表1)。同时,对作为解释变量的工业专业化指数以及作为被解释变量的流通业全要素生产率进行了详细的描述分析。将我国工业专业化指数按照<0.2、0.2~0.3、0.3~0.4、0.4~0.5、>0.5 进行等级划分,作出 2012 年和2016年我国工业专业化指数空间分布图(见图1)。由2012年工业专业化指数空间分布图可以看出,我国东中部地区大部分省份的工业专业化指数处于0.2~0.3阶段,安徽省和山东省处于<0.2阶段,而相对不发达的西部地区的工业专业化指数处于0.3~0.4、>0.5两个阶段,表示西部地区的工业专业化程度较高。由2016年工业专业化指数空间分布图可以看出,全国范围内较多省份的工业专业化指数有所下降,只有内蒙古出现了上升趋势。由此可以看出,我国工业专业化指数分布较明确,西部地区的工业专业化程度比东中部地区高,且全国范围内的工业专业化程度呈现下降趋势。
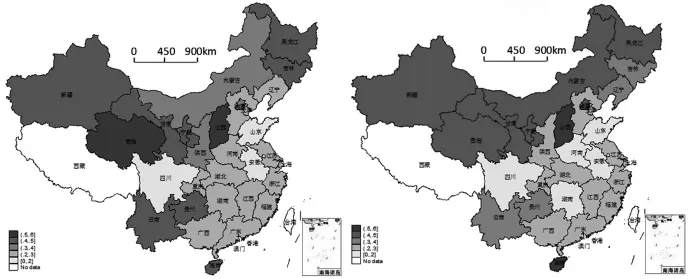
图1 我国2012年(左)和2016年(右)工业专业化指数空间分布图
我国各省份的流通业全要素生产率通过DEA-Malmquist指数法计算而来,将流通业全要素生产率按照 <0.85、0.85~0.9、0.9~0.95、0.95~1.0、>1.0进行等级划分,作出2012年和2016年我国流通业全要素生产率空间分布图(见图2)。由2012年流通业全要素生产率空间分布图可以看出,我国南部省份和北部省份的流通业全要素生产率处于0.95~1.0、>1.0 两个阶段,甘肃、青海、安徽、四川、贵州等省份较低。结合2016年流通业全要素生产率空间分布图来看,我国大部分省份的流通业全要素生产率都出现了下降的情况,只有四川、重庆、湖北三省及直辖市出现了明显的增长。
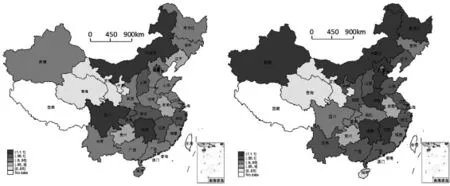
图2 我国2012年(左)和2016年(右)流通业全要素生产率空间分布图
为了更加直观地观察工业专业化指数对流通业全要素生产率的动态影响,绘制出了各省市地区的工业专业化指数与流通业全要素生产率之间相对应的散点图和简单拟合直线(见图3),从图中可以看出,两者之间的拟合直线明显呈现向下倾斜趋势,说明工业专业化指数与流通业全要素生产率之间存在一种负相关关系。同时,可以发现东中部省份的散点较为集中,大多集中于(0.25,0.95)处,说明东中部省份的情况较为相似。而西部地区省份的散点较为分散,主要是西部省份之间的流通业全要素生产率较为分散。从上述分析可以看出,工业专业化指数越大,即工业专业化程度越高,其地区流通业全要素生产率越小。
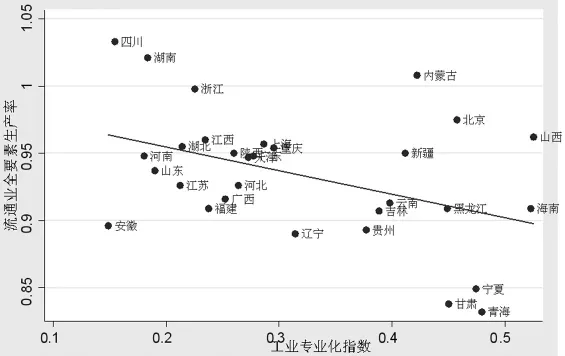
图3 工业专业化与流通业全要素生产率
三、实证分析
本文使用计量软件Stata14.0对面板数据进行了回归分析。在实证检验中,考虑到工业集聚与流通效率之间存在双向因果关系,因此,作为解释变量的工业专业化指数与随机扰动项存在相关性,直接使用随机效应模型的GLS估计量或固定效应模型的LSDV估计量,会造成估计结果是有偏和非一致的,这就造成了模型的内生性问题。解决模型内生性问题的一个有效办法就是工具变量法,本文采用了工业增加值的对数(LNSA)作为工具变量,并进行了传统的豪斯曼检验(Hausman-test),P 值为 0.519,接受原假设,所有解释变量均为外生,但由于传统的豪斯曼检验(Hausman-test)建立在同方差的前提下,在存在异方差的情景下不成立,所以进行异方差稳健的杜宾-吴-豪斯曼检验 (DWH-test),P值为0.0344,在显著性水平为5%的条件下,拒绝原假设,因此,可以认为工业专业化(H)为内生解释变量。同时,进行了异方差检验,P值为0,chi2为1058.33,拒绝原假设,存在异方差,因此使用GMM比2SLS更好。GMM动态面板数据模型不仅仅可以使用模型外部的工具变量,还可以使用面板数据模型内部提供的工具变量,可以有效解决模型的内生性问题。下面,本文将采用动态面板数据的系统GMM模型进行回归分析。
(一)总体样本的回归分析
表2是我国30个省市总体样本的回归结果。模型1是不考虑工业专业化指数(H)的内生性问题及其与流通业全要素生产率(TFP)的非线性关系的情况下,探究工业专业化指数(H)与流通业全要素生产率(TFP)之间关系的固定效应回归结果,结果显示,工业专业化指数(H)的系数为0.7502,且在5%的显著性水平下显著,说明工业专业化指数(H)对流通业全要素生产率(TFP)存在显著的正向作用,与图三显示的结果不一致。模型2是考察工业专业化与流通业全要素生产率之间是否存在“U型”关系的固定效应回归结果,结果显示,工业专业化指数(H)和其平方项的系数分别为2.4417、2.0686,分别在1%、5%的显著性水平下显著,说明工业专业化与流通业全要素生产率之间存在显著的正“U型”关系。模型3和模型4分别是不控制地区虚拟变量和控制地区虚拟变量的系统GMM模型回归结果,从AR(1)和AR(2)的结果中可以看出,两个模型的扰动项的差分均存在一阶自相关,但均不存在二阶自相关,故接受估计模型中的扰动项无自相关的原假设。同时,Sargan test工具变量过度识别检验结果也显示,在10%的显著水平下,无法拒绝所有工具变量均有效的原假设,这证明了两个模型设定的合理性和工具变量的有效性。综合考虑,本文最终将使用模型4的回归结果进行分析。
模型4的回归结果显示,工业专业化指数(H)的回归系数在1%的显著水平下为负,而其平方项的回归系数在1%的显著水平下为正,表明工业专业化与流通业全要素生产率之间存在显著的正 “U型”关系,即存在“工业专业化陷阱”。经过估算,当工业专业化指数(H)在0.34344时,流通业全要素生产率达到最小值,位于正“U型”的最低点。在达到这个最低点之前,工业集聚即工业专业化会抑制流通业全要素生产率的增长;一旦越过这个最低点,工业专业化将促进流通业全要素生产率的增长。结合图1、图2和图3进行解释,我国发达省份的工业规模较大,从而工业难以专业化发展,但是工业规模较大的背后必定带来较大规模的流通业需求,从而促进流通业全要素生产率的增长。我国部分欠发达省份由于地理位置以及资源禀赋等因素,其工业专业化程度较高,同时形成流通专业化发展,促进了流通业全要素生产率的增长。模型中的工业专业化与流通业增加值的交互项(H×LNCVA)的回归系数为正,通过了10%的显著性水平检验,表明流通业规模越大的省份工业专业化对流通业全要素生产率的促进作用越大,即工业专业化对流通业的规模效应为正。在控制变量中,研发强度(R&D)和城镇化(CITY)的回归系数显著为正,说明研发强度(R&D)和城镇化(CITY)都可以促进流通业全要素生产率(TFP)的增长;产业结构(IS)和外资流入程度(FDI)的回归系数为负,但未通过10%的显著性水平检验,说明其二者不利于流通业全要素生产率 (TFP)的增长;政府规制(GOV)的回归系数为正,也未通过10%的显著性水平检验,说明政府规制促进了流通业全要素生产率(TFP)的增长。
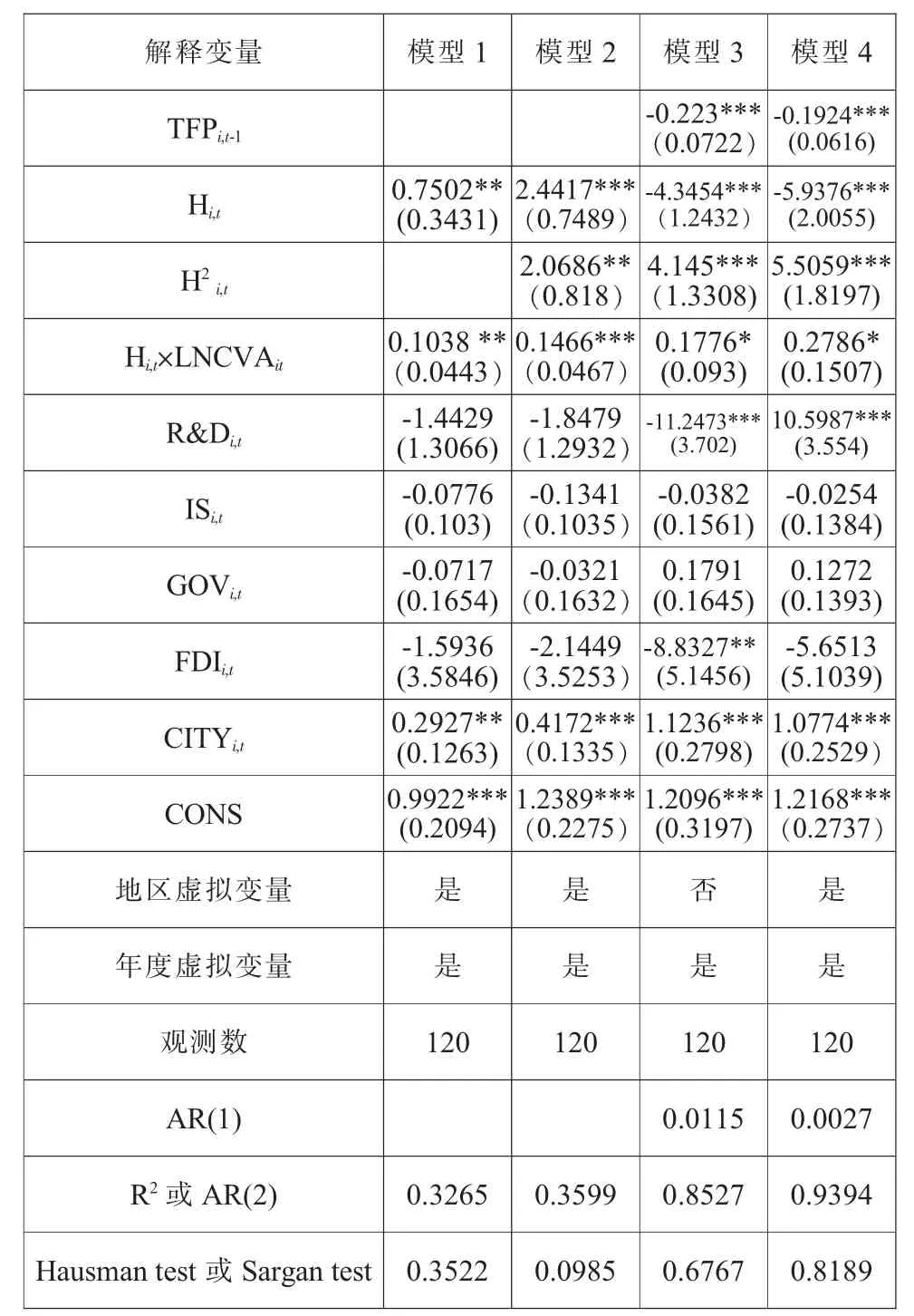
表2 工业集聚对流通业全要素生产率影响的实证结果(全国层次的估计)
(二)按地区分样本的回归分析
为了进一步探究工业集聚的专业化效应对流通业全要素生产率影响的区域性差异,本文将全国30个省市分为东部、中部、西部三个地区样本,其中,东部地区包括北京市、天津市、上海市、辽宁省、河北省、山东省、江苏省、浙江省、福建省、广东省和海南省;中部地区包括黑龙江省、吉林省、山西省、河南省、安徽省、江西省、湖北省和湖南省;其余省份为西部地区。均使用系统GMM模型对三个地区的工业专业化对流通业全要素生产率的影响进行了回归分析,从表3的估计结果中可以看出,三个模型的AR(2)均显示扰动项的差分不存在二阶自相关,故模型中的扰动项无自相关。同时,三个模型的Sargan test工具变量过度识别检验结果也显示,在10%的显著水平下,无法拒绝所有工具变量均有效的原假设。以上检验证明了三个模型设定的合理性和工具变量的有效性。
回归结果表明,在东部、中部和西部地区,工业专业化与流通业全要素生产率之间均存在正“U型”关系,东部与中部地区分别在1%和10%的显著性水平下显著,而西部地区未通过10%的显著性水平检验,说明西部地区工业专业化与流通业全要素生产率之间存在的正“U型”关系比较微弱。这与三个地区的省份经济规模分布不均匀有关,东部各省份的经济规模比较分散,中部地区次之,但西部属于欠发达地区,其各省市经济规模较为集中,样本数据的集中导致模型回归结果的显著性较差。经过估算,东部、中部和西部地区的工业专业化指数(H)分别达到0.21964、0.35911和0.48237时,其流通业全要素生产率将达到最小值,位于正“U型”的最低点。与全国样本分析结果同理,在达到这个最低点之前,工业集聚即工业专业化会抑制流通业全要素生产率的增长;一旦越过这个最低点,工业专业化将促进流通业全要素生产率的增长。三个地区的工业专业化与流通业增加值的交互项(H×LNCVA)的回归系数均为正,中部与西部地区分别通过了1%和10%的显著性水平检验,而东部地区未通过,说明东部地区的工业专业化对流通业规模的影响比较微弱。这一结果出现的一个可能原因在于,东部地区在观察期内一直保持较低的工业专业化程度,且变动幅度较小,导致工业专业化对流通业规模的影响较小。同时,在东部地区的回归结果中,政府规制(GOV)的回归系数在1%的显著性水平下显著为负,而中部与西部地区的回归系数为正,且西部地区的回归系数也通过了1%的显著性水平检验,这意味着我国政府规制效应从西部向东部地区逐阶递减,特别是在东部地区出现了负作用的现象,可能由于东部地区市场经济比较发达,政府规制过大会抑制市场的发展,会导致适得其反的作用。外资流入程度(FDI)的系数在三个地区样本中也不一致,东部与中部地区为负,而西部地区为正,且均不显著,这可能是各地区对外资的需求程度差异的反映,西部地区的地理位置和资源禀赋等现实情况决定了其对外资需求程度较高,外资对流通业生产率的拉动作用较强。
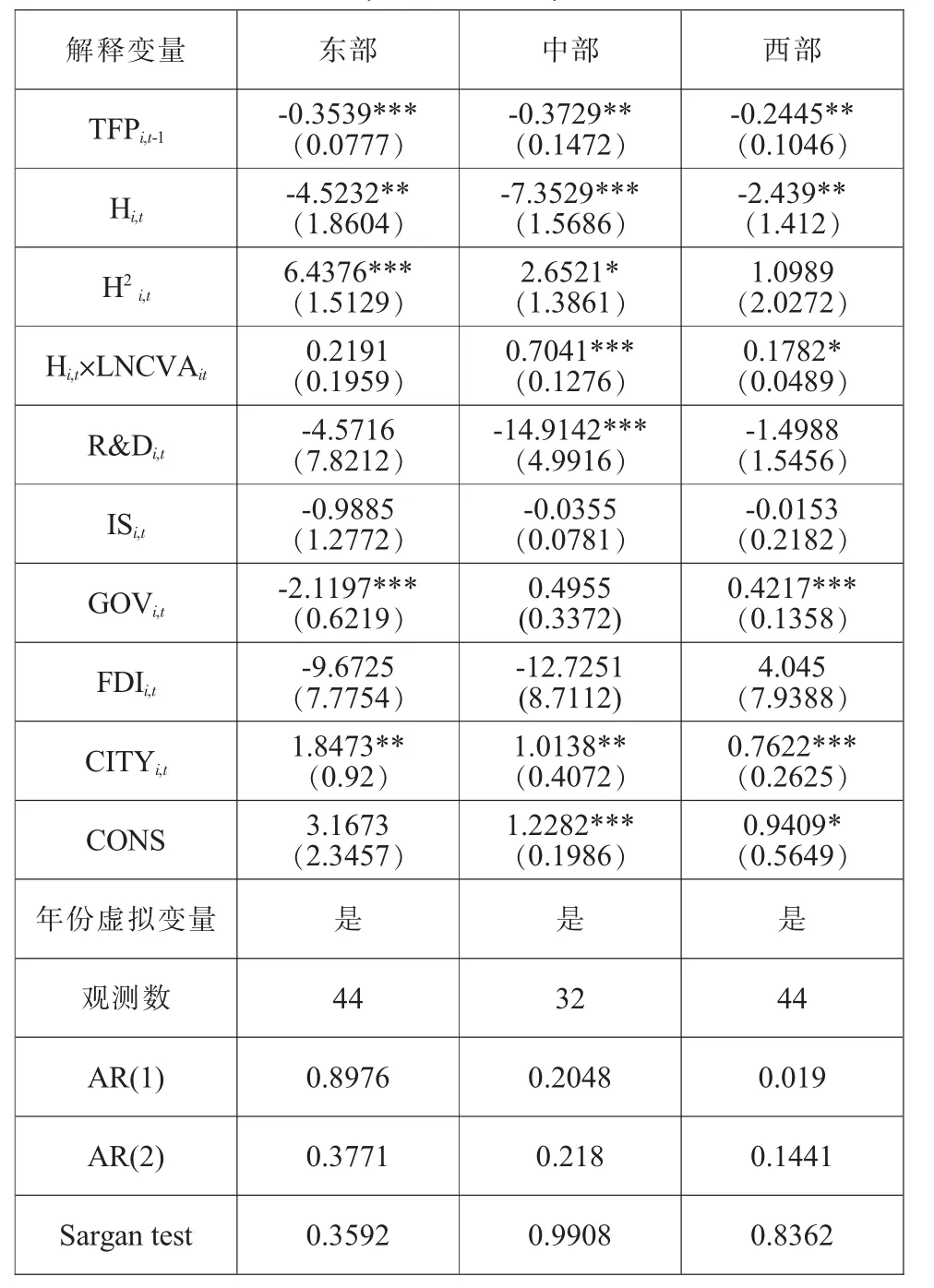
表3 工业集聚对流通业全要素生产率影响的实证结果(分地区估计)
四、结论和政策建议
本文利用2012—2016年间我国30个省市的面板数据,使用系统GMM模型克服模型内生性问题的前提下,探讨了工业集聚的专业化效应对流通业全要素生产率的动态影响。研究发现,总体而言,当前我国工业结构偏向于多样化,即工业专业化程度较低,但也存在显著的地区差异,东部和中部地区的工业专业化程度较低,而西部地区的工业集中于初级产品部门,因此工业专业化程度较高。同时,全国层次样本分析结果表明,工业专业化与流通业全要素生产率之间存在显著的“U型”关系,但仍然存在显著的地区差异,相较于东部和中部地区,西部地区工业专业化与流通业全要素生产率之间存在的正“U型”关系比较微弱。在其他控制变量的影响关系上也存在一定的地区差异,我国政府规制效应从西部向东部地区逐阶递减,特别是在东部地区出现了负作用的现象;同时,西部地区的外资流入程度对流通业全要素生产率的拉动作用比东中部地区更高。
因此,在大力推动工业与流通业价值链互动发展的过程中,需要注重各地区的工业结构调整,东部与中部地区更应向多样化方向发展,而西部地区受地理位置的限制和资源禀赋的影响,其工业更应向专业化方向发展。同时,中部和西部地区应该增强政府规制程度,可以有效提高流通业效率。西部地区还应建立健全市场体系和基础设施,积极吸引跨国公司进行投资。重视流通业与工业的协同发展,这对于提高流通效率、扩大工业规模以及促进地区经济发展具有积极意义。

