具有不同转折角度的复杂单裂隙水头损失试验研究
张春艳,束龙仓,张帅领
(1.华北水利水电大学 地球科学与工程学院,河南 郑州 450046; 2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098; 3.中国电建集团河南省电力勘测设计院有限公司,河南 郑州 450007)
裂隙是岩溶含水系统的基本构成单元,是岩溶含水系统主要的储水空间和导水通道。因此,研究裂隙中的水流运动规律对于岩溶含水系统的水动力过程研究具有重要的意义,是岩溶水科学研究的基本任务[1]。同时,单一裂隙渗流研究也是岩体裂隙网络渗流规律及裂隙岩体渗流场与应力场耦合作用研究的基础和关键[2-3]。
鉴于裂隙介质的非均质性及各向异性,国内外越来越多的研究者利用室内物理模型进行裂隙水流运动规律的研究。陈舟[4]利用自制的交叉粗糙裂隙进行试验,分析了低流速单进双出交叉裂隙的水流特征。孙莉琴[5]指出粗糙单裂隙中水流运动规律可以用Forchheimer和Izbash方程描述。Javadi等[6]研制了三维人工裂隙,设置不同的入口流速,选取不同的横、纵剖面研究不同入口流速条件下的流速分布,结果表明,入口流速越大,流速分布越接近对称。严小三等[7]利用大理石平板裂隙进行试验,得出了裂隙中非达西流和非费克运移的结论。束龙仓等[8]、王熹等[9]分别针对直角裂隙和平行裂隙中水头损失的变化规律进行了试验研究。Zhang等[10]探讨了平行裂隙中达西流和非达西流的界限以及立方定律的适用范围。刘日成等[11-12]基于最小二乘法对人工交叉裂隙的水力学开度进行了探讨,试验得出流速与压力之间呈二次函数关系,可用Forchheimer方程描述。桑盛等[13]研究了“人”字交叉裂隙开度、交叉角度对流量分配特性的影响。陈雷等[14]研究了隙宽和粗糙度对单裂隙中非达西流比例的影响,隙宽越小,粗糙度越大,非达西渗流比例越大。杨欢欢等[15]利用Fluent软件模拟研究了交叉裂隙中的偏流现象,结果表明,在高速非达西条件下,偏流现象更显著。程勤波等[16]选取野外垂向与水平向交叉裂隙的岩石剖面,进行了单环注水入渗试验,并利用立方定律和N-S方程进行了数值模拟。综合前人研究结果,对于裂隙水流运动规律的物理试验研究,大多集中于平行单裂隙、简单交叉裂隙以及正交裂隙网络中水流运动规律的研究,转折角度对裂隙水流运动影响的研究较少,裂隙水流运动的机理研究有待进一步发展[17],本文利用自制裂隙物理模型,系统地研究不同裂隙开度、转折角及流速条件下,裂隙水流的运动特性。
1 物理模型
为研究角度对裂隙渗流特性的影响,设计研制了不同交叉角的复杂单裂隙,两组裂隙面(L1,L2所在裂隙面)分别平行,两组裂隙面间有一定夹角(β),示意图见图1。

图1 复杂单裂隙示意图Fig.1 Schematic diagram showing the complex-single fracture
本次共设计制作了不同裂隙开度(b,1~2.6 mm之间变化),不同角度(β,分别为15°,30°,45°,60°,90°,105°,120°,150°,165°共9个不同的角度)的裂隙共30个。裂隙尺寸及角度见表1。

表1 复杂单裂隙尺寸表Table 1 Sizes of the complex-single fractures
2 试验装置、原理及水头损失计算方法
2.1 装置及原理[8]
利用自主设计的室内物理试验装置监测裂隙水头随时间的变化,水头变化测量装置示意图,见图2。

图2 裂隙水头变化测量装置示意图Fig.2 Schematic diagram showing the experimental device of hydraulic head measurement1—注水筒; 2—压力传感器; 3—导水管; 4—连接管; 5—裂隙
图2(a)中,以通过裂隙出流口中心的水平面为基准面,取水面线所在的断面与裂隙出流口过水断面为控制面,两个控制面由能量方程得:
(1)
同理,图2(b)中,以通过连接管出流口中心的水平面为基准面,取水面所在的断面与连接管出流口过水断面为控制面,两个控制面由能量方程得:
(2)
连接管管口与裂隙口的大小基本一致,故此连接处的局部水头损失可忽略。适用于式(1)及式(2)。
式中:H1、H2——有、无裂隙条件下的水头差/cm;
α——动能校正系数,取α=1;
v1、v2——有、无裂隙条件下,水流出流口的流速/(cm·s-1);
g——重力加速度,取g=980/(cm·s-2);
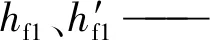

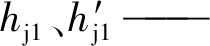


hw——水流经过裂隙的水头损失/cm。

(3)
对于某一开度的裂隙,需要知道有、无裂隙条件下试验过程中的水头差H1、H2以及出口流速v1、v2,可由式(3)计算得到水流流经裂隙时的总水头损失hw。
2.2 试验操作
步骤1: 取裂隙开度为b1的裂隙,按照图2(a)连接试验装置。
步骤2:连接装置后,开启阀门1,注水筒水注入至一定高度后关闭阀门1。打开阀门2,水流从裂隙口流出,打开阀门2的同时,压力传感器控制系统开始记录水头变化数据,直至水面线降至0-0′基准面,关闭阀门2。
步骤3:移除裂隙,此时试验装置见图2(b),打开阀门1注水筒水注入至一定高度后关闭阀门1。打开阀门2,水流从连接管管口流出,打开阀门2的同时,压力传感器控制系统开始记录水头变化数据,直至水面线降至0-0′面,关闭阀门2(此时,裂隙开度为b1的裂隙水头变化测量试验结束。操作此步骤时注意移除裂隙前后要保持装置其他部分一致)。
步骤4:更换连接管(不同开度的裂隙,裂隙口大小不一,需用不同的连接管连接),取不同开度的裂隙重复步骤2、3。
2.3 裂隙总水头损失hw的求解
由试验操作步骤二、三采集到的试验数据,可以得到有裂隙及无裂隙条件下水头差随时间变化的关系曲线见图3。
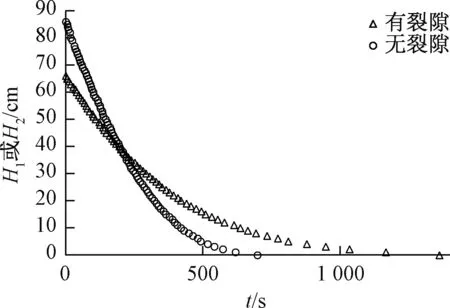
图3 有、无裂隙条件下,水头差H1或H2随时间变化Fig.3 Hydraulic head difference vs. time under conditions with fractures or without fractures
假设水头差随时间变化的表达式为:
H=H(t) (4)
Δt时间间隔内的流量变化表达式为:
(5)
式中:H——水头差/cm;
Δt——时间间隔/s;
S——注水筒截面面积/cm2。
有、无裂隙条件下,水头差H与裂隙出流口流量关系曲线见图4。利用Matlab程序进行曲线拟合,得到H1=H1(Q)和H2=H2(Q)。

图4 开度b1及无裂隙水头差随出口流量变化曲线Fig.4 Hydraulic head difference vs. discharge under conditions with aperture width b1 and without fractures
3 试验结果及分析
3.1 裂隙总水头损失hw计算结果
分别取转折角β小于90°,等于90°,大于90°三个不同的角度为例介绍复杂单裂隙总水头损失随流速的变化曲线,其他角度的裂隙变化曲线类似,此处不再赘述。不同裂隙开度,不同折角条件下,裂隙总水头损失hw随流速变化见图5(a)~(c)。
从图5可以看出,不同转折角条件下,水流流速较小时,裂隙总水头损失hw与裂隙开度之间没有明确的关系,然而随着流速的增大,总水头损失hw随裂隙开度的增大而增大,这主要是由于裂隙开度增大导致局部水头损失增大,即使裂隙开度增大导致沿程水头损失减小。
对总水头损失hw与流速v之间的关系进行拟合。结果表明,hw与v之间存在二次函数关系:
hw=Awv2+Bwv(6)
不同折角,不同裂隙开度条件下,系数Aw与Bw取值变化见图6(a)~(b)。从图中可以看出,裂隙开度越大,二次系数Aw越大,而系数Aw与折角之间没有明确的关系。不同折角,不同裂隙开度条件下,系数Aw位于上包线y=0.013 5x-0.005 1以及下包线y=0.013 5x-0.017 0之间。一次系数Bw取值比较均匀,绝大多数取值位于-0.1~0.5之间。
3.2 裂隙局部水头损失hj计算结果
对于开度小于1.463 5 mm的裂隙,利用修正立方定律计算裂隙平行部分的水头损失(hf),对于开度大于1.463 5 mm的裂隙,利用达西-魏斯巴赫公式计算平行部分的水头损失[10],公式中的圆管直径d由矩形过水断面的水力半径代替计算,再由hw—hf得到局部水头损失hj。
不同裂隙开度,不同折角条件下,裂隙局部水头损失hj随流速变化见图5(d)~(f)。局部水头损失主要由复杂单裂隙的折角β导致。与总水头损失hw变化相类似的是,水流流速较小时,不同折角条件下,局部水头损失与裂隙开度之间没有明确的关系,然而随着流速的增大,局部水头损失随裂隙开度的增大而增大。
对局部水头损失hj与流速v之间的关系曲线进行拟合。结果表明,hj与v之间存在二次函数关系:
hj=Ajv2+Bjv(7)
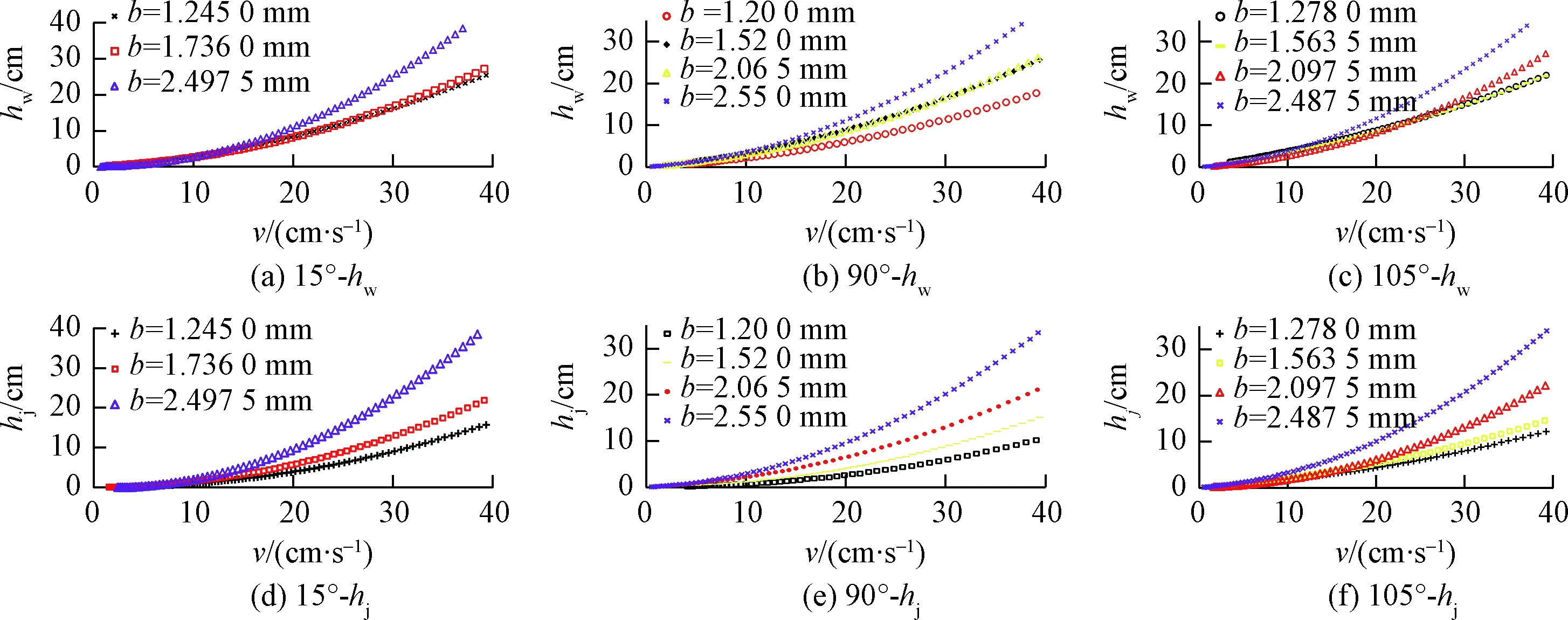
图5 不同裂隙开度,不同折角条件下,裂隙总水头损失hw和局部水头损失hj随流速变化Fig.5 Total hydraulic head loss of fractures and local hydraulic head loss of fractures vs. flow velocity under conditions of different aperture widths and turning angles
不同折角,不同裂隙开度条件下,系数Aj与Bj取值变化见图6(c)~(d)。从图中可以看出,裂隙开度越大,二次系数Aj越大,系数Aj与折角之间没有明确的关系。不同折角,不同裂隙开度条件下,系数Aj位于上包线y=0.014 4x-0.007 9以及下包线y=0.014 4x-0.018 1之间。一次系数Bj取值比较均匀,绝大多数位于-0.1~0.25之间。

图6 不同折角,不同裂隙开度条件下,二次系数Aw,Aj与一次系数Bw,Bj取值变化Fig.6 Changes of two times coefficients Aw,Aj and one time coefficients Bw,Bj with different aperture widths and turning angles
4 结论
(1)裂隙总水头损失hw以及局部水头损失hj与平均流速v之间存在二次函数关系,可用Forchheimer公式描述。
(2)hw—v关系的二次项系数取值分布于上包线y=0.013 5x-0.005 1以及下包线y=0.013 5x-0.017 0之间,一次项系数取值分布于-0.1~0.5之间。
(3)hj—v关系的二次项系数取值分布于上包线y=0.014 4x-0.007 9以及下包线y=0.014 4x-0.018 1之间,一次项系数取值分布于-0.1~0.25之间。

