冷轧工作辊变形分析

崔 钺 王会刚 王丽元

(1: 唐山学院机电工程系 河北唐山 063000；2: 河钢集团唐钢公司炼铁部 河北唐山063016)

1 前言

随着冷轧板带及其涂镀层产品市场空间的不断提升，对冷轧板带的板型要求也逐渐提高。板形问题贯穿于板带的整个生产过程，存在于轧制的各个环节。影响板形的因素很多，如轧机的刚度、轧辊凸度、弯辊力、来料的品种以及原始凸度、轧制工艺等等。而在实际的轧制过程中，可以进行在线调控的只有轧制力与弯辊力，只有在轧制力与弯辊力在轧制过程中不断匹配修正，才能实时控制轧制过程中有载辊缝，达到控制冷轧带钢最终板型的目的[1-2]。

弯辊力是通过液压系统向工作辊或中间辊轴颈加载的力，用以改变轧辊的有效凸度，从而通过改变承载辊缝形状来改变轧后带钢沿横向的延伸变形，达到板型控制的目的，对于消除对称板带材缺陷的中浪、边浪等作用明显。弯辊力可实现工作辊的正弯与负弯，正弯指的是向增大工作辊的接触凸度；负弯指减小工作辊的接触凸度。但一方面考虑到轴承的承载能力，弯辊力不能过大，另一方面，弯辊力对辊缝边部的影响大于中部辊缝的影响。

2 轧制力模型

考虑带钢冷轧时弹性变形和塑性变形两种状态，引入Bland-Ford-Hill轧制力模型，其中，总轧制力F由塑性区轧制力Fp与弹性区轧制力Fe构成[3]：

F=FP+Fe

(1)

(2)

(3)

(4)

ξ=αtin+βtout

(5)

式中：F-轧制力,kN；

Fp-塑性轧制力,kN；

Fe-弹性区轧制力,kN；

QF-轧制力外摩擦影响系数；

W-带钢宽度,mm；

R′-轧辊压扁半径,mm；

hin-带钢入口厚度,mm；

hout-带钢出口厚度,mm；

v-泊松比；

E-杨氏模量,MPa；

μ-摩擦系数；

γ-压下率；

tin-带钢入口单位张力,MPa；

tout-带钢出口的单位张力,MPa；

α、β-带钢入口与出口的张力影响系数。

km-平均变形抗力,MPa,取决于金属材料塑性变形时的物理条件:

(6)

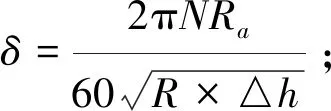
N-轧机转速,r/min；

t-轧制温度,℃；

k0-基准变形阻力,MPa；

a1-a6-回归系数。

3 有限元模型：

以唐钢第一钢轧厂平整分卷机组的四辊平整机为例建模，实现工作辊正负弯辊力的四个锻钢弯辊缸块装在牌坊之间，并带有16个液压柱塞缸，压力由比例阀控制。两个压下液压缸安装在牌坊和上支承辊轴承座之间。

按照轧辊和轧件的实际尺寸建立有限元模型,为提高计算效率，近似模型为上下对称，模型参数见表1，建立的有限元模型见图1。

表1 模型参数(mm)

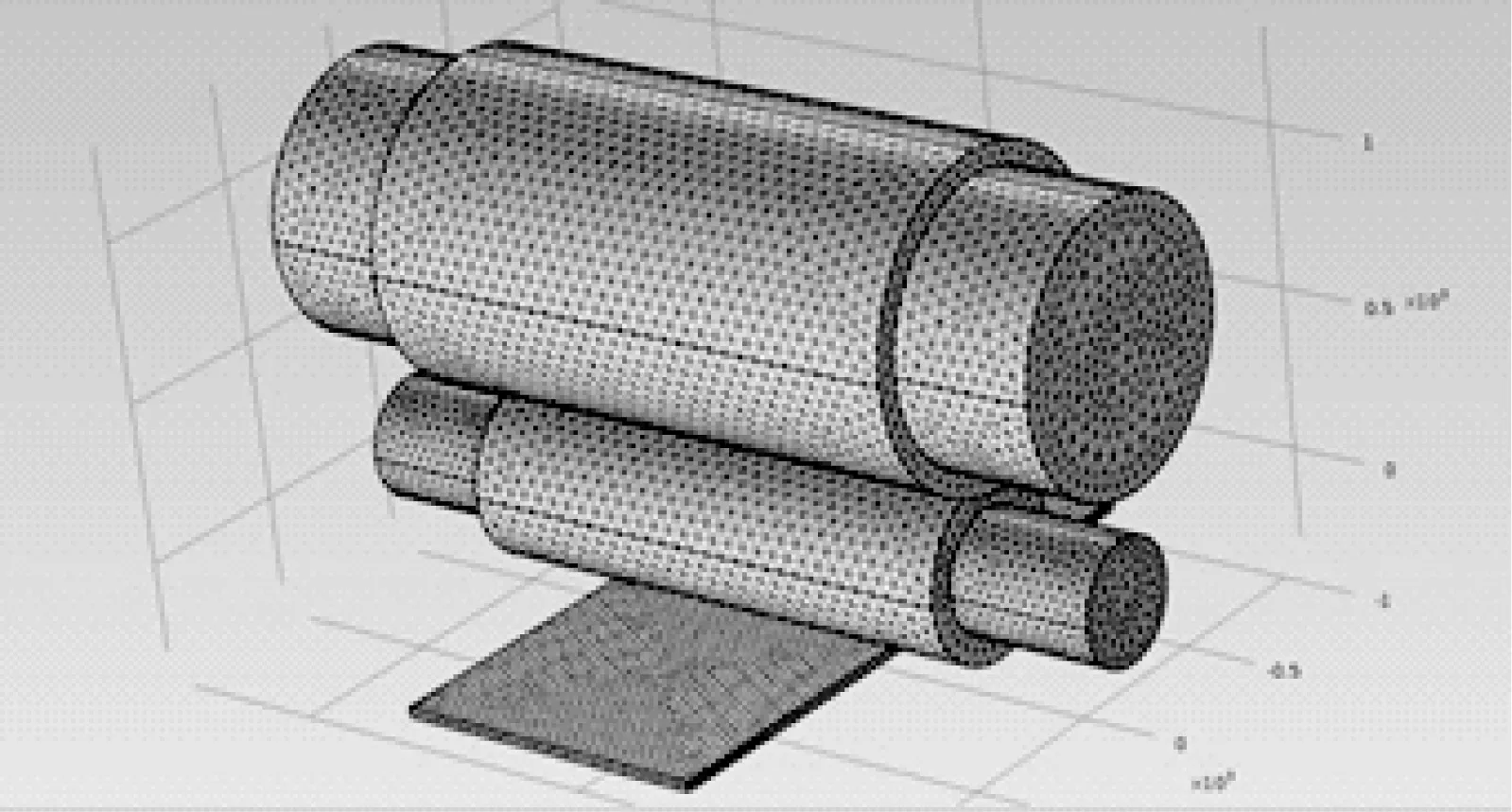
图1 有限元模型网格划分

在该模型中，工作辊设置为弹性体(假设其初使凸度为0)，用以模拟工作辊的弹性弯曲变形和弹性接触变形，轧件作为弹塑性体，采用Bland-Ford-Hill轧制力模型与库伦摩擦模型[4-5]，根据等效应力屈服准则判定。参数化建模对称稳态求解，板带下底面加固定约束，加载轧制力与弯辊力的边界载荷至支撑辊与工作辊的轴颈端面。

4 结果分析

对支撑辊轴颈加载4400kN的轧制力，对工作辊轴颈加载弯辊力-400kN，作工作辊的Von Mises等效应力与应变分析。

由图2，工作辊与带钢接触表面处最大Von Mises等效应力值出现在带钢侧边与工作辊接触的位置，最大值450MPa；支撑辊与工作辊的轴颈区域、带钢侧边与工作辊接触的位置均出现等效应力值的升高。

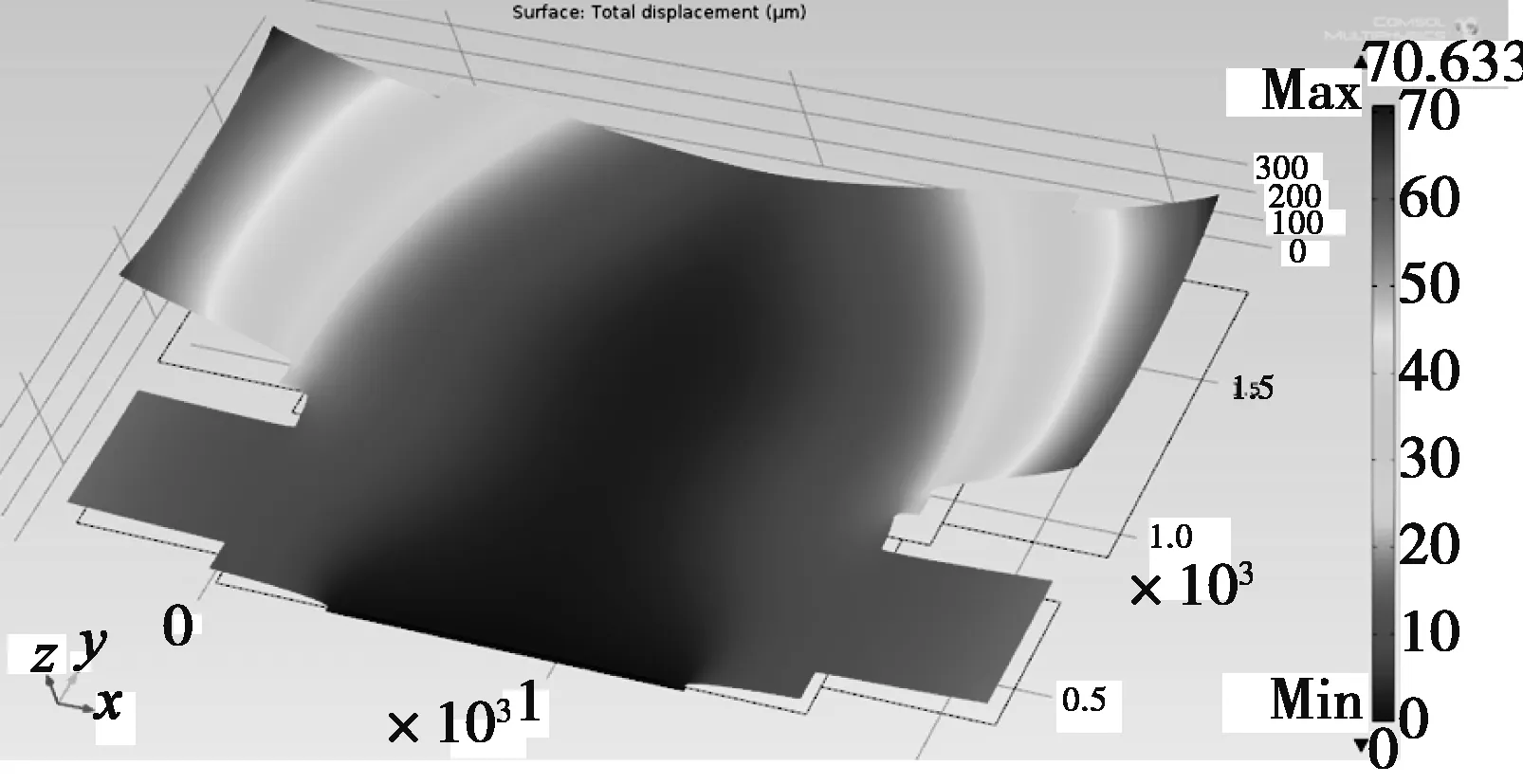
图2 轧辊中截面变形高程表达图

由图3轧辊中截面变形高程显示，轧辊中出现的最大变形发生在支撑辊辊颈的轧制力加载区域，最大值约为70μm。沿支撑辊与工作辊的辊径方向，出现了较明显的变形区域。

图3 工作辊轴线、底面及与板带接触位置在铅直方向的变形(μm)

图4为整理的工作辊轴线、底面及与板带接触位置在铅垂方向的变形，其变化趋势类似；工作辊轴颈与工作轴间存在小范围的挠度突变；工作辊底面变形较轴线位置严重，整体凸度接近-18，而在与1000mm宽度的带钢接触面上凸度变形较小，保持-8左右。

随后保持4400kN轧制力不变，作不同弯辊力(-400～400kN)工作辊底部变形分析：

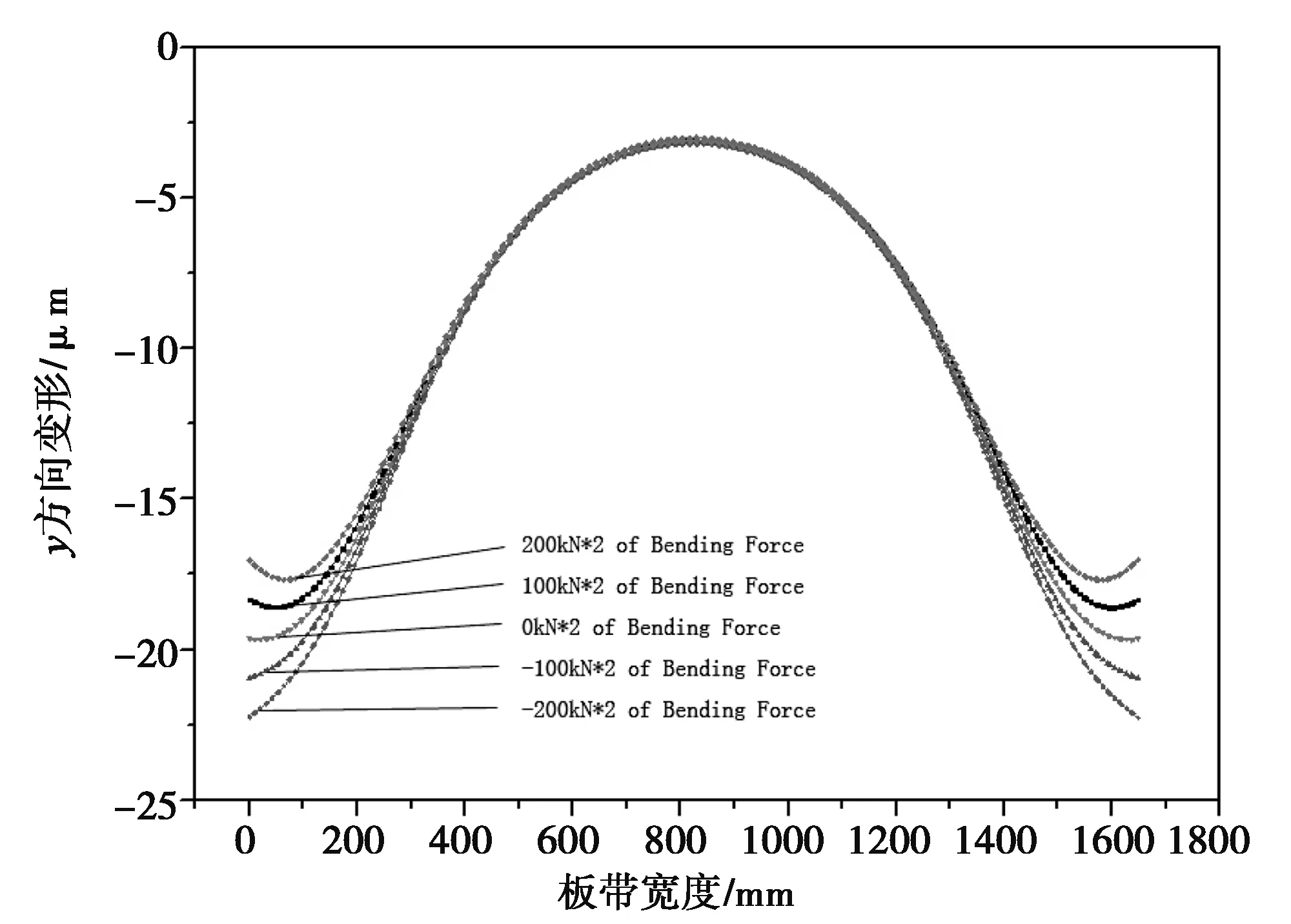
图4 不同弯辊力下工作辊底面变形

图5 不同轧制力工作辊底面变形

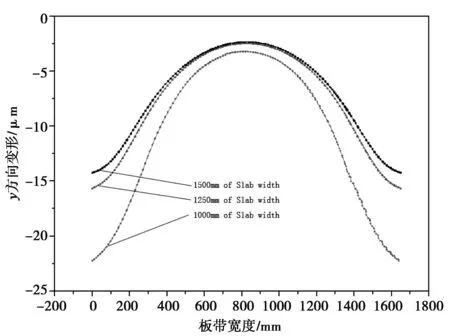
图6 4400kN轧制力、-400kN弯辊力下不同板带宽度工作辊底面铅直方向变形

图5为控制轧制力4400kN不变，弯辊力由-400kN至400kN下工作辊底面在铅垂方向的变形，随着弯辊力的不断增大，工作辊的整体凸度也随之增大，最小值发生在弯辊力-400kN时，凸度为-20；图6为控制弯辊力0kN不变时，轧制力在2000kN至4400kN变化时工作辊底面在铅垂方向的变形情况，工作辊底面凸度随轧制力的增大而减小，其最小值发生在轧制力4400kN时，凸度值为-18。

作4400kN轧制力、-400kN弯辊力，得到不同板坯宽度时工作辊底面在铅直方向的变形(图6)，随着板带宽度的增大，工作辊底面的凸度也随之增大；轧辊对宽板坯的凸度控制更好。

表2 实测板型参数与模拟凸度对比

对平整机入口和出口的带钢进行留样，对比实测板型参数与模拟参数，模拟得到的板型凸度与实测凸度变化规律相似，且随着板带宽度的增加，模拟凸度更贴近于实测值，最大值为1.36。

5 结论

以Bland-Ford-Hill轧制力模型为基础，针对唐钢第一钢轧厂平整分卷机组的四辊平整机，以轧制力与弯辊力为相互影响参数，进行了四辊平整机的有限元计算，得到结论如下：

1) 轧辊的最大变形发生在支撑辊辊颈位置，发生疲劳失效的可能性较高；

2) 控制轧制力4400kN不变，弯辊力由-400kN增至400kN时，工作辊的整体凸度也随之增大，最小凸度为-20；

3) 控制弯辊力0kN不变时，轧制力在2000kN至4400kN变化时，工作辊整体凸度随轧制力的增大而减小，最小值为-18；

4) 对比实测板型参数与模拟参数，模拟得到的板型凸度与实测凸度变化规律相似，且随着板带宽度的增加，模拟凸度更贴近于实测值。