空冷过程T型钢放置角度对温度场分布影响

邹昶方 陈 猛

(中冶华天工程技术有限公司 江苏南京210019)

1 前言

终轧温度约为900℃的T型钢，上冷床后进行空冷，其传热模式为在高温段向空气热辐射为主、低温段与空气对流为主及型钢内部的热传导。由于其断面的非对称特性及重力因素，断面各部分的冷却速度差别很大，从而引起断面上温度的不均匀分布，进而导致T型钢弯曲变形。

冷床冷却能力是制约T型钢生产能力的重要因素之一。影响冷床冷却能力以及断面温度分布的因素很多，比如冷床的长度及其周围的结构物、冷床上齿条的齿形角度等。目前，冷床的设计以单根圆棒的实验空冷时间为主要依据，这对于异型断面的型钢而言很不准确。在数值研究方面[1]-[4]，当前的文献对型钢空冷的研究主要基于有限元法，其存在的主要问题是直接赋予换热系数，而这个换热系数是经过大量简化得到。

基于此，本文采用多场统一建模方式，流场(空气)与结构场(型钢)变量统一求解，并系统地研究了在不同的放置角度下，T型钢冷却时间及断面温度分布的规律，其研究结果可为实际的冷床齿形倾角设计提供依据。

2 数学模型

2.1 控制方程

T型钢空冷牵涉到的力学机理有：高温型材的热传导、热辐射；常温空气由于温度梯度的影响产生流动以及流动空气与型材的热对流。其具体的数学模型如下。

(1)连续性方程

(1)

式中：ρ-流体密度;

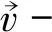
(2)N-S方程

(2)

μ-粘度;

p-压力。

(3)能量方程

(3)

式中：Γ-比内能;

Cp-比热容;

λ-导热率。

(4)导热微分方程

(4)

式中：T-温度；

qv-内热源在单位时间、单位体积产生的热量。

(5)对流传热

q=h(Ts-Ta)

(5)

式中：h-对流换热系数；

Ts-固体表面温服；

Ta-周围流体温度。

(6)辐射传热

(6)

式中：q-热流率；

ε-辐射率

σ-斯蒂芬-玻尔兹曼常数;

A1-辐射面1的面积;

F12-由辐射面1到辐射面2的形状系数；

T1、T2-辐射面1和2的绝对温度。

2.2 耦合边界条件

对于固体周围有流体的传热问题，综合考虑流体与固体的耦合传热，在流固耦合边界上通过耦合边界条件把流场与结构场联系起来统一求解。此时，流固耦合面上的换热系数是根据物理问题自身的机理计算得到，而不是人为的简化获得，这种力学描述更加接近真实的物理模型，其计算结果也更加可靠。其耦合边界应满足温度及热流连续条件：

TC|s=Tc|f

(7)

qc|s=qc|f

(8)

式中：TC-流固耦合面的温度；

qc-通过耦合面的热流密度；

s-指固体；

f-流体。

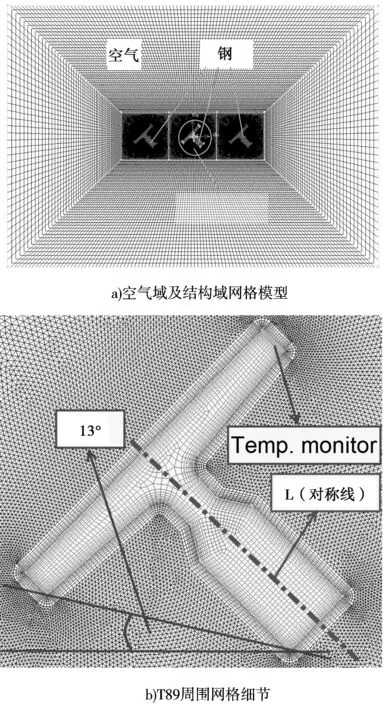
图1 T89空冷计算模型

3 数值计算模型

3.1 网格构建

本文以T89为研究对象，考虑到空冷过程，冷床上多根型钢之间相互影响，建模时选取三根T型钢，其网格如图1所示。

3.2 物性参数及计算工况

文中钢种为40#碳素钢，高温棒材的比热容与导热率同样依赖于温度[5]，其值如表1所示。计算初始条件为棒材1000℃。文中T型钢的在冷床上的放置角取13°、19°、25°及31°。

表1 钢材热物性参数

4 结果分析及讨论

4.1 放置角对T89冷却时间的影响

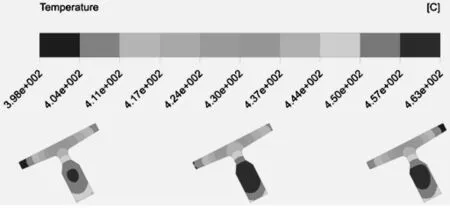
对于放置于冷床上的T89，在空冷过程中选取图1(b)中所示的监测位置来研究温降时间及换热系数，其温降时间曲线及换热系数与温度关系曲线分别如图2、图3所示。

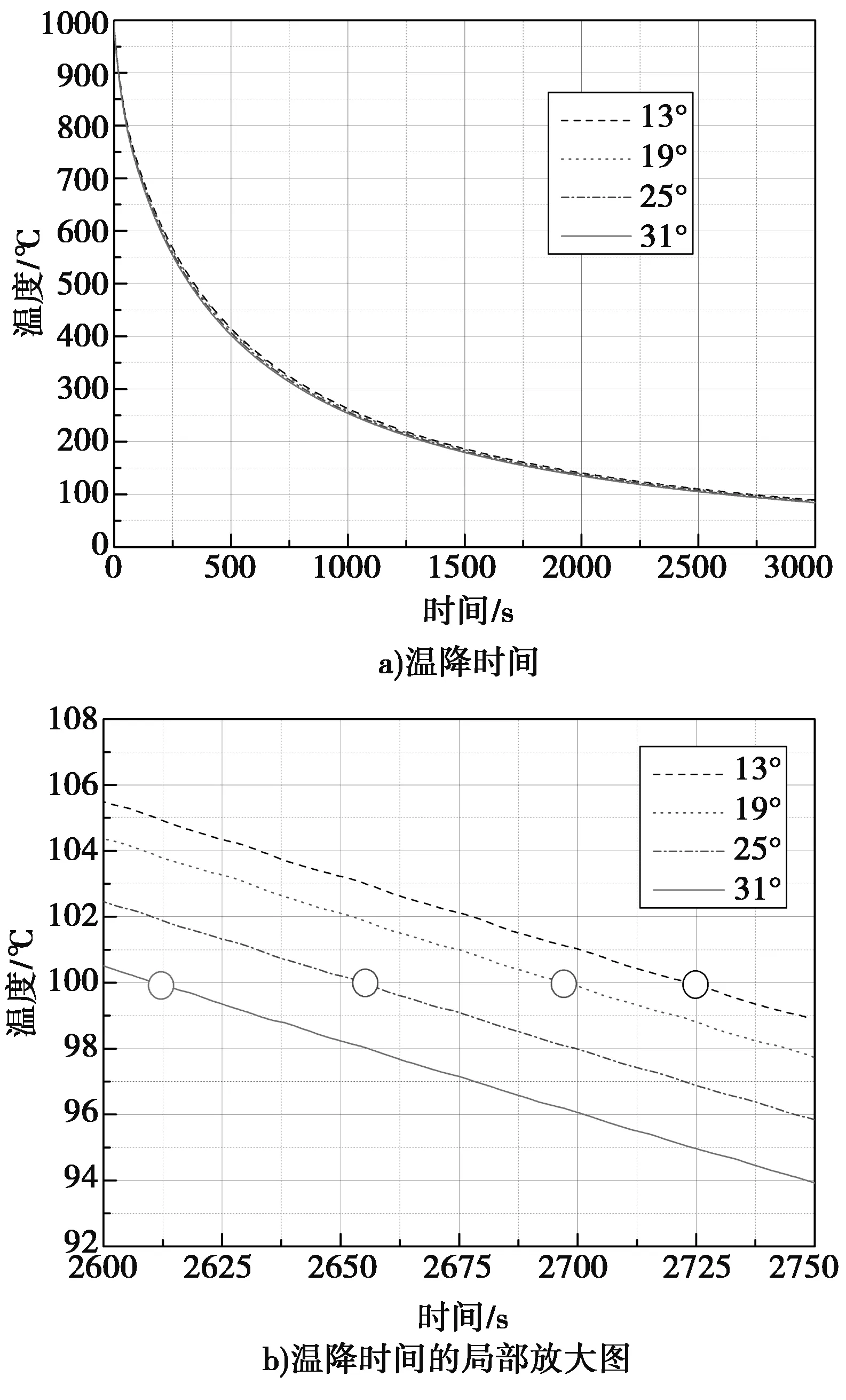
图2 不同放置角下的空冷温降时间曲线

由图2可见，T型钢以13°、19°、25°及31°四种放置角度置于冷床上，由1000℃降至100℃所需时间分别为2725s、2698s、2655s及2612s。随着放置角度的增加，其温降时间减小；放置角由13°

增加到31°，温降时间也仅仅减小了113s，因此，放置角度对温降时间的影响很小。

整个空冷过程T型钢的传热模式是：高温段以向空间辐射为主，低温段以自然对流为主。由图2中温降曲线的斜率变化可以得出整个空冷过程型钢向空间辐射传热是最主要的传热模式。

图3 T89表面换热系数与温度关系

由图3可见，空冷过程型钢在600℃～1000℃之间，放置角度对表面换热系数有明显影响；600℃以下，尽管放置角度不同，但是表面换热系数基本一致。这说明在高温段，型钢放置角度对以向空间辐射为主的传热模式有重要影响；而在低温段，型钢放置角度对以自然对流为主的传热模式几乎没有影响。

4.2 温度场分布特征分析

由图4(a)知，型钢向周围的空气传递热量，周围的热空气在浮力作用下上升，带走热量，这是自然对流现象。在轨底与轨腰相交的下角隅处，会密集大量的高温空气，由于轨底的阻挡，这些高温气体不易在浮力作用下进行上升流动，导致T89断面上的温度关于L线呈不对称分布。

a)放置角31°时的全场温度分布

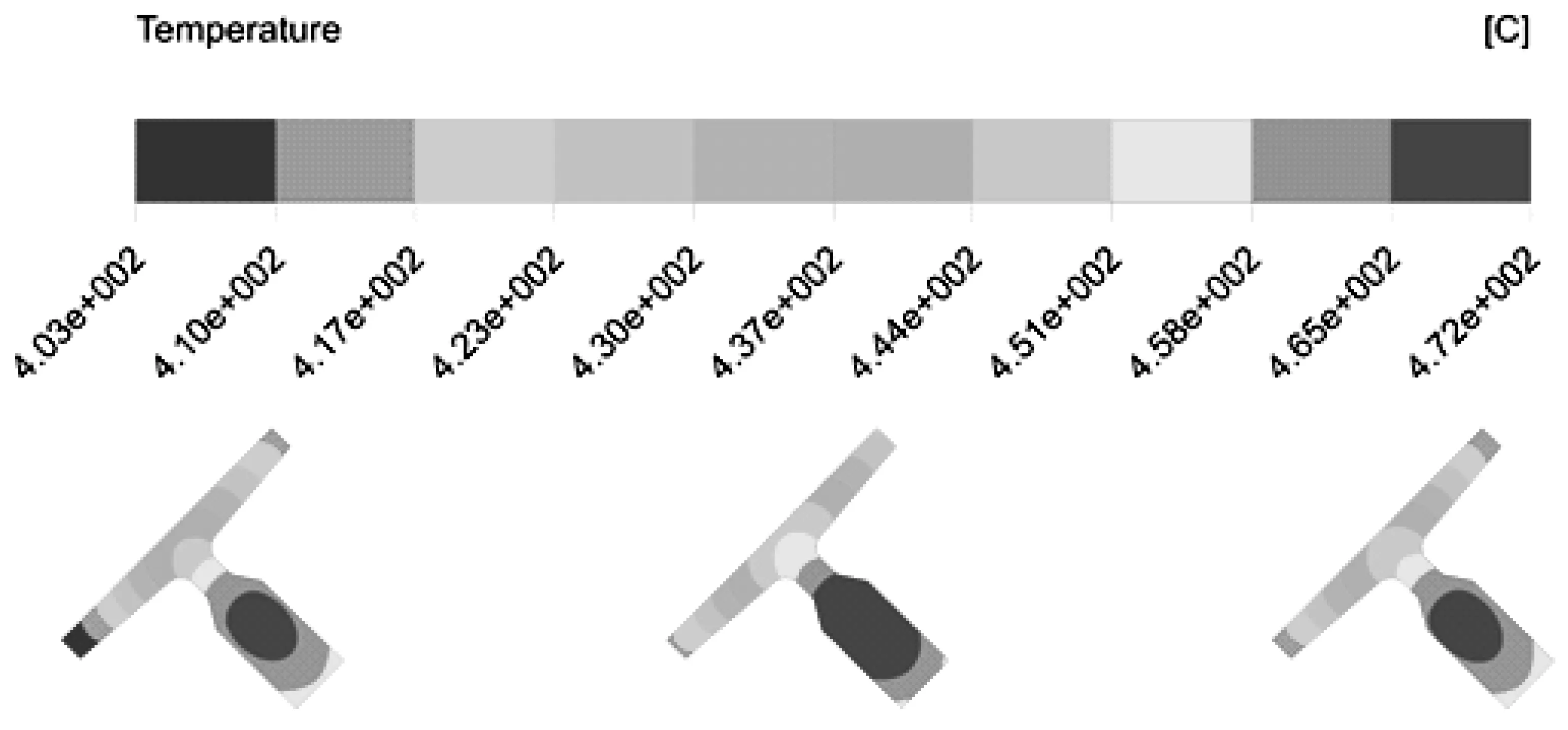
b)放置角13°时T89的温度分布

c)放置角19°时T89的温度分布

d)放置角25°时T89的温度分布

e)放置角31°时T89的温度分布

由图4(b)-(e)可见，轨头中部温度最高，轨头顶部及轨腰次之，轨底端部温度最低。正是由于这种在断面高度方向上的温度不均匀分布，引起断面上的不均匀热应力，这是导致T型钢空冷后弯曲变形的根本原因。轨头中部与轨底端部的温差最大，放置角分别为13°、19°、25°及31°时，其温差分别为69℃、66℃、64℃及65℃；此时会产生由轨底弯向轨头的弯曲变形，但是在25°放置角度时的弯曲变形最小，13°时最大。尽管如此，在13°放置角下，轨底两个端部的温差要小于25°工况，这说明在小的放置角下T89空冷过程不易发生侧弯，而大的放置角除了产生轨底弯向轨头的弯曲变形外还有侧弯变形。

5 结论

本文针对型钢T89在冷床上空冷过程进行数值研究，分析了不同放置角度对其冷却时间及断面温度场分布的影响。本文的主要研究结论包括：

(1)尽管随着放置角度的增加，空冷时间减小，但是其影响较小。

(2)高温型钢向空间的辐射传热在空冷过程起主导作用；放置角度对高温阶段的换热系数有明显影响，对低温阶段的换热系数影响很小。

(3)轨头中部与轨底端部的温差在25°的放置角时最小，在13°时最大；但是在25°时轨底两个端部的温差要大于13°的工况，表明在25°放置角下，除了产生轨底弯向轨头的弯曲变形外还有侧弯变形。