基于模糊综合评判的在线图像分割
林坚普,王卫星,2,严 群,郭太良,姚剑敏,林志贤,白莉娜
(1.福州大学 物理与信息工程学院,福州 350108;2.瑞典皇家工学院,斯德哥尔摩SE-10044)
经过爆破或者自然崩落法采集的矿岩块,其尺寸和形状的分布是评价生产质量的重要指标。传统的测量方式主要是人工测量和统计,最常用的方法是制作不同尺寸的筛子进行块度的筛分。但在骨料(矿岩块度)生产中,由于矿岩块度的坚硬程度和设备材质,以及设备磨损等因素的影响,导致筛分测量效率不够高,而且设备的投入成本较大,效益低。所以,研究一种方法快速准确地获取矿岩块的形状及尺寸参数信息对提高生产效率及生产自动化程度有实际意义。自20世纪末开始,随着数字图像处理和分析技术的快速发展,人们开始将图像处理技术应用于矿岩块度的测量与分析及在线检测/监测系统中[1-6]。在20世纪90年代也曾研发过矿岩块度测量和分析系统[1]:一种是人机交互的测量分析系统;另一种是在线检测系统。近几年来,这方面的研究越来越多[2-6],但热点之一仍然是运输带上矿岩块度的精确提取问题。为了避免块度重叠及表面纹理和三维信息给从运输带上获取的图像分割带来的困难,本文的检测系统在传送带末端利用CCD视频相机,以天空为背景,获取空中降落的矿岩块度图像并进行实时在线处理(见图1)。该方法能够获取清晰的矿岩块度在空中的投影并可对图像进行实时的全天候测量和分析,并对生产质量做出评价及自动控制。

图1 矿岩块度在运输带上及降落流中的情况对比Fig.1 Comparison of rock fragments on a conveyor belt and in a falling stream
为了满足在线检测系统的实时性要求,阈值分割算法是图像分割的一个较好的选择。基于灰度的阈值分割主要是根据图像中的灰度差异,将图像分割为目标和背景两类。传统的全局阈值分割算法针对目标和背景亮度对比度较大的图像有较好的分割效果,但是对于本文的矿岩块度图像,由于天气及灰尘等变化原因,图像中会存在矿岩块度的阴影及噪声,此外还存在一些的块度粘连现象,以至于用全局阈值算法无法完全将矿岩块度检测出来。为了克服这一弊病及减少算法的运算量,我们研究了一种基于模糊综合评判的自适应动态阈值分割算法,该算法先对图像进行全局阈值分割,提取各岩块区域参数信息并进行模糊综合评判,根据判决结果对需要的块度区域或异常尺寸及形状的区域,再利用阈值分割算法求取新的局部阈值,重复这一操作,直到每一块度无可再分为止。算法简单,运算快,可达到精度要求,算法流程如图2所示。
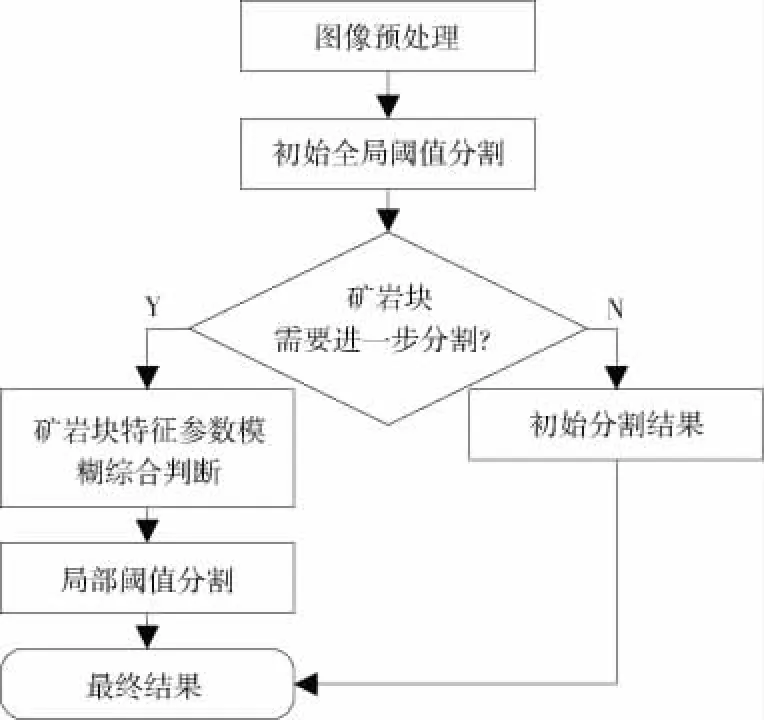
图2 矿岩块度图像模糊自适应阈值分割算法流程Fig.2 Working flowchart of adaptive fuzzy thresholding algorithm for rock fragment images
1 图像预处理和初始分割
1.1 图像的预处理
监测系统采集的图像是彩色图像,先要对图像进行灰度化处理,以便后续处理。本文图像背景多为蓝色,而红色成分较弱,故加大蓝色的权值,减少红色的权值,根据彩色图像的RGB值,转换为灰度图像的灰度值公式如下,即灰度值X为:
X=0.11R+0.59G+0.3B
在采集图像的过程中,图像不可避免地受到各种因素的干扰,致使图像中存在一些噪声。由于光线不均,图像中还存在不清晰问题。这些问题会给后续工作带来困难,较好的图像预处理可以降低这些因素的影响。因此,图像的预处理主要是对图像进行平滑滤波处理。这里采用中值滤波方法来去除或减少那些噪声及保持似粘连部分的弱边界。初始处理后的结果如图3所示。

图3 原始图像及其预处理图像Fig.3 Original image and its preprocessed result
1.2 图像初始分割
初始分割利用经典阈值分割算法对图像进行全局分割,全局分割是指对整幅图像进行阈值分割。这样的算法很多,为了选取合适的算法,本文选取应用较为广泛的阈值分割算法,如:最大类间方差法(Otsu法)、最大熵法、矩保持法、迭代法。这些算法的基本思路是:对图像的像素灰度值运算,确定一个灰度阈值T(0≤T≤255),根据阈值T将整幅图像分成两个区域:目标区域和背景区域。在目标区域中,所有的像素点的灰度值小于这个阈值,故在二值图像里,目标区域像素点的值设为0;而背景区域的像素点的灰度值小于这个阈值,在二值图像里将背景区域的像素点值定为255。阈值运算后得到二值化的图像可用如下公式所示:
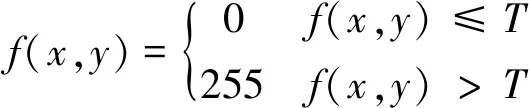
(1)
阈值分割算法的结果很大程度上依赖于对阈值的选取,因此阈值分割算法最重要的就是选取合适的阈值,这也是图像分割算法的关键,下面简单介绍几种经典的阈值分割算法。
最大类间方差法(Otsu法)又称大津法[7],是日本学者大津展之在1979年提出的一种全局阈值分割算法。其基本思想是假设阈值将图像分为目标区域和背景区域,然后分别计算这两个不同区域中的像素点个数和平均灰度值,再求目标和背景区域之间的类间方差,最后求解使得类间方差最大且类内方差最小的对应灰度值T作为阈值。矩保持法是Tsai于1985年提出的[8]基于图像矩的多阈值分割算法,其原理是在阈值分割运算前后,保持图像的矩不变。最大熵法的作者Kapur[9]认为图像中的目标物体和背景区域是两种不同的信号源,当这两类区域的熵之和为最大值时,那个对应的灰度值也就是要求解的阈值。由熵的定义可知,如果图像中灰度值差异小,则熵大,所以如果选取的阈值合适,图像被分割后的结果中,各区域内灰度值的差异较小,信息量大,即熵最大。所以,找到目标与背景区域熵最大时对应的灰度值即阈值。迭代法是先设定整幅图像的一个阈值,将该初始阈值分割后得到的区域分别看作子图像,然后利用子图像再计算全局阈值,重复上述过程,直到所求得的阈值与前次阈值相等时,将此时的阈值作为最终的阈值。图5及表1数据是几种阈值算法的例子。
对图像取全局阈值时,目标区域和背景区域的差异反映在图像的直方图中就是在两个较大的波峰中有相对明显的波谷,求图像的全局阈值就是要找到这个波谷。采集到的矿岩块图像直方图多为波谷较明显的图像(图4),利用上述算法得到的阈值,都基本上落在直方图的波谷区,但最好算法的选取还要根据图像分割结果来说明(图5和表1)。
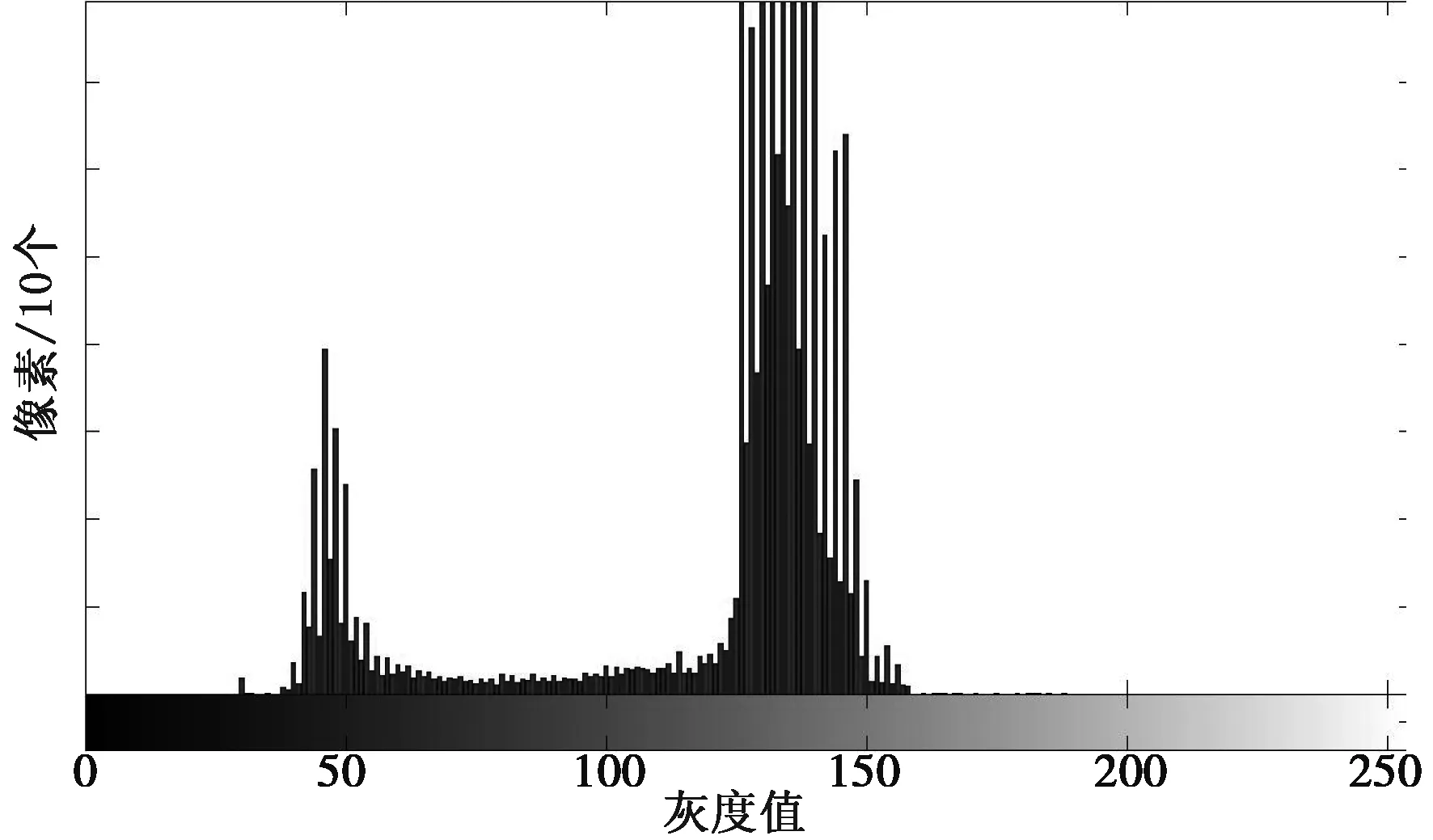
图4 图像直方图Fig.4 Image histogram
当图像被预处理后,我们先利用全局阈值算法对图像进行初始分割。经过对比多幅岩石块度图像(图像序号0~300)的初始分割结果,并统计全局阈值算法的阈值,我们得到:在表1中,大津法和迭代法要相对好一些,剩余的另两种方法所得到的全局阈值过大,致使粘连的岩石块度较多,给进一步分割造成困难。而进一步的试验说明:迭代法阈值算法的结果与初始阈值选取有关,初始阈值的设置有时可导致整幅图像全黑或全白。对比结果说明无论从速度还是从稳定性来说,大津法阈值算法都是最佳的阈值算法选择。所以,我们在初始阈值分割和进一步阈值分割时,都选取大津法作为基础算法。再进一步的分割就是要分离粘连在一起的岩石块度。

图5 不同的阈值分割算法分割结果 Fig.5 Results of threshold algorithms:(a) Original image;(b) Otsu result; (c) Iteration result;(d) Moment-preserving result;(e) Max entropy result
2 基于模糊评判的图像分割
初始全局阈值算法分割后的图像为二值图像,在此基础上,根据矿岩块度的不同特征进一步分割。全局阈值分割是直接利用整幅图像的灰度差异特性区分出目标和背景。但对于细节的地方,效果不一定很好。在未分离的矿岩块度之间有阴影,及微弱灰度差异的共有区域,利用全局阈值无法分割,所以针对矿岩块度之间有粘连现象的情况,利用粘连矿岩块度的多种特征作为判断准则,作进一步图像分割。
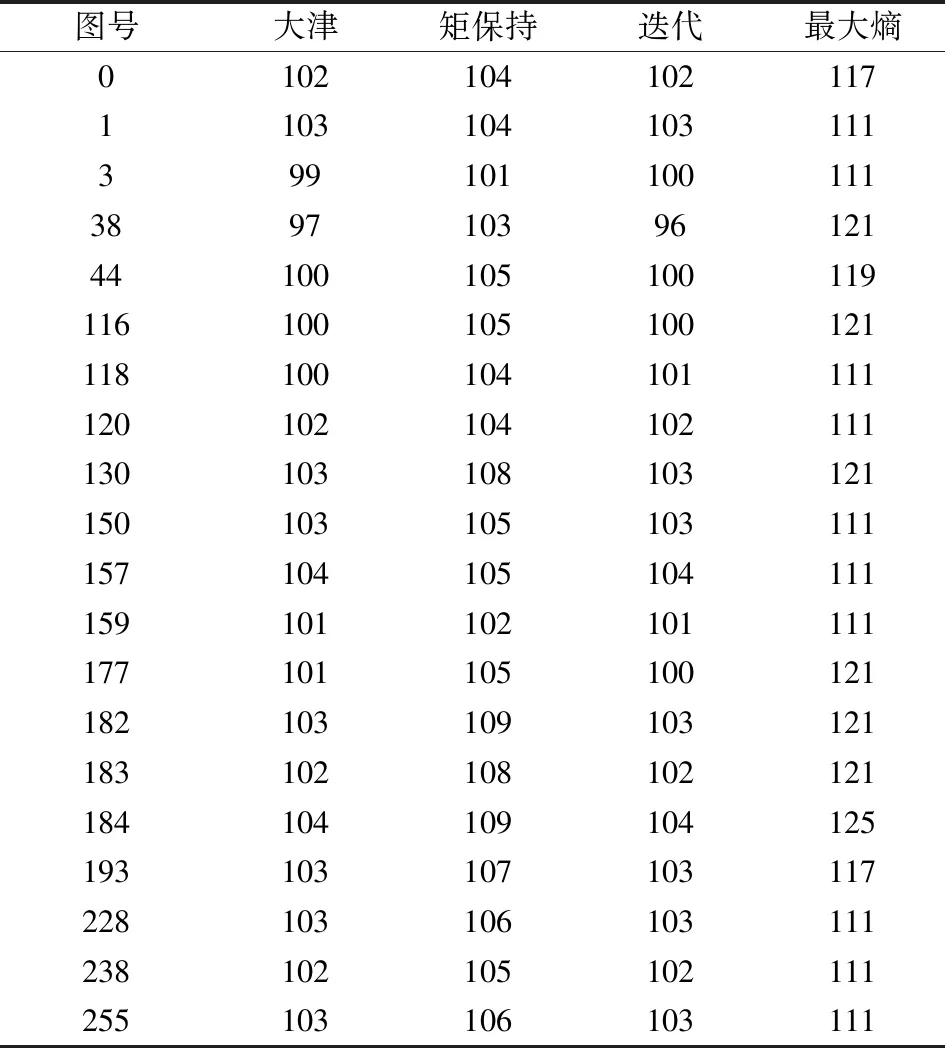
表1 几种阈值分割算法全局阈值数据结果
2.1 区域特征参数定义
利用尺寸和形状特征,可以较为简捷地分离粘连的矿岩块度[10-13]。矿岩块度一般为不规则的多边形凸包域,对于目标区域的尺寸和形状描述主要有以下几种:
1)目标的面积计算
从初始分割后的图像中可以看出,粘连在一起的目标物体最显著的特征就是面积太大。面积的计算非常简单,求出区域边界及边界内像素点的总和即可[14-15]。
2)目标的周长计算
目标的周长在区别具有简单或复杂形状物体时非常重要。由于数字化的周长的表示方法不同,所以计算方法也不同,为简便起见,我们用目标物体边界上的像素之和来表示周长。
3)区域的形状因子
这里的形状因子是用来描绘一个区域与圆形接近的程度,圆形的形状因子为1,区域的形状与圆形的差别越大,其形状参数与1的差值也就越大[16-17]。其定义如下:
(2)
式中:L—区域周长,S—区域面积。
4)区域内部梯度
图像目标区域边界上的像素点,在对应的灰度图像中,其邻域是灰度值的变化带。梯度可以有效地衡量灰度值的变化。图像在任意点的微分值大小可以表示灰度的变化率大小,因而我们用一阶微分的值来定义梯度,若图像为f(x,y),在某点(x,y)处的梯度值可定义如下:
(3)
常用差分来近似微分,典型的梯度差分算法,表示为:
(4)
5)区域内部的平滑度
图像的平滑度是图像的平滑特征之一,我们用图像区域的灰度方差来表示图像的平滑度。其定义如下:
(5)
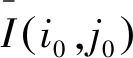
2.2 矿岩块度参数模糊综合评判
若将岩块的参数信息作为进一步阈值分割的依据时,有多个因素需要考虑。如果只单独考虑某个因素,无法得到较为准确的判断。而且每一个目标区域是否需要作进一步分割,多半都是模糊的,为此,可以采用模糊数学中的模糊综合判断方法来进行判断,结合图像特性的几个主要因素来对每一目标区域进行判断。模糊综合评判的思想是利用模糊线性变换原理和最大隶属度原则来考虑与被评价事物相关的各种因素,从而对其做出较为合理的综合评价[18]。
模糊综合评判的主要三要素为:
1)确定因素集:U={u1,u2,…,um}
2)设计评语集:V={v1,v2,…,vn}
3)顾名思义,单因素判断就是对单个因素ui(i=1,2,…,m)的评判,得到V上的F集(ri1,ri2,…,rin),所以它是从U到V的一个F映射,F映射f可以确定一个F关系R∈μm×n,R为评判矩阵。
(6)
各评判因素相对评判结果有不同决定性,需要对各因素做加权处理。用A=(a1,a2,…,am)表示各因素的权重分配。权重集与评判矩阵合成得到综合评价集B(b1,b2,…,bn),模糊综合评价集是针对各因素的综合评判的结果,最后根据模糊数学中的最大隶属度原则,选取模糊综合评价集中最大的评语作为评价的结果。
由岩石块度参数组成的因素集是整个模糊综合评判的基础,其关系到评判结果的真实性和可靠性。选择的因素应能全面地反映岩石块度基于灰度及形状的特征。故此我们选取分割后的目标区域的面积、周长、形状、梯度和平滑度为因素集成员。模糊综合评判的结果(即评语集)由需进一步分割和不需进一步分割组成。每个因素权重值的确定方法很多,一般的方法有统计法和层次分析法等。其中,统计法需要请多位行业专家对因素集中的各个元素给出认为最合适的权重,然后再进行统计分析。而评判矩阵的确定则需要知道各个因素单独对评价的影响,这个评判矩阵由每个因素的隶属度构成,而隶属度的确定是很关键的步骤,要能够稳定地表示每个因素属于每个评价的频率。通常隶属函数的确定方法有许多,如推理法、模糊统计方法、三分法、二元对比排序法等。模糊统计方法要进行大量的统计实验,然后用逻辑推理的结果来确定。例如:若确定论域U上固定的元u0是否属于论域上的一个模糊集合A*的隶属度,那么u0是固定的,A*是动态的集。通过做n次模糊统计实验,就可以确定隶属度:
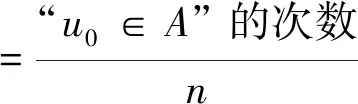
随着n的增大,隶属频率呈现稳定性,稳定的频率就是u0对A的隶属度。通过模糊统计大量的矿岩块度图像,由观察统计图像上矿岩块度的粘连状况得到每一区域各个因素对评价集的隶属度,再通过曲线拟合,得到隶属函数。经过统计,各个因素稳定在某一个隶属值,由这些隶属值所组成的隶属函数分别为(该拟合函数图如图6):
面积的隶属函数:(见图6)
F(x)=0.008131x9-0.03741x8-
0.001882x7+0.2197x6-0.2257x5-
0.303x4+0.5725x3-0.227x2-
0.01311x+1.008
拟合的结果质量评价参数:
SSE: 0.75,R-square: 0.982 3
周长的隶属函数(见图5):
F(x) = 0.007753x9-0.03216x8+
0.2362x7-0.1396x6-0.4537x5+
0.5318x4-0.04068x3-0.09318x+ 1.01
拟合结果的质量评价参数:
SSE: 2.007,R-square: 0.936 1
形状因子的隶属函数(见图5):
F(x)=0.006222x+0.4685(x<50)
F(x)= -0.02712x4+0.1385x3-
0.1587x2-0.1711x+
0.7113 (50≤x≤275)
F(x)= 39.63x9-91.06x8-77.39x7+
193.1x6+88.61x5-111.6x4-
48356x3+12.94x2+6.111x+
0.8071(x>275)
拟合结果的质量评价参数:
SSE: 7.29, R-square: 0.4807
梯度的隶属函数(见图5):
F(x)=0.3408x+0.2591 (x<30)
F(x) =0.02721x9-0.1422x8+0.1277x7+
0.398x6-0.65481x5-0.1142x4+
0.4862x3-0.07631x2-0.06878x+
0.1478 (30≤x≤208)
F(x)= 0.1546x4-0.2838x3-0.2729x2
+0.7091x+0.7214 (x>208)
拟合结果的质量评价参数:
SSE: 0.666 5,R-square: 0.875 6
平滑度的隶属函数(见图6):
F(x)=0.3532x+0.337(x<68)
F(x) =0.1113x4-0.05123x3-
0.4865x2-0.1153x+
0.6175 (68≤x≤200)
F(x)= 0.1238x2-0.07593x+0.2963
(x>200)
拟合结果的质量评价参数:
SSE: 1.145,R-square: 0.8072
当拟合函数时,原始的数据先经归一化,再经中心化,其中心化方式为:
(7)
式中:x—原始的数据,mean—x均值,std—标准差。相应地,以上隶属函数中的x均经过中心化和归一化的数据。这里函数分段标准则是按归一化后的数据进行的。拟合的数值与实验的数据存在一定误差,衡量拟合结果质量优劣之评价参数是:
1)误差平方之和SSE:The sum of squares due to error
2)确定系数:R-square
评价拟合曲线时,SSE越接近0,曲线的拟合效果越好,当R-square越接近1,曲线的拟合效果将越好。每条拟合曲线的质量参数都如图所示,拟合效果均为较好(见图6)。
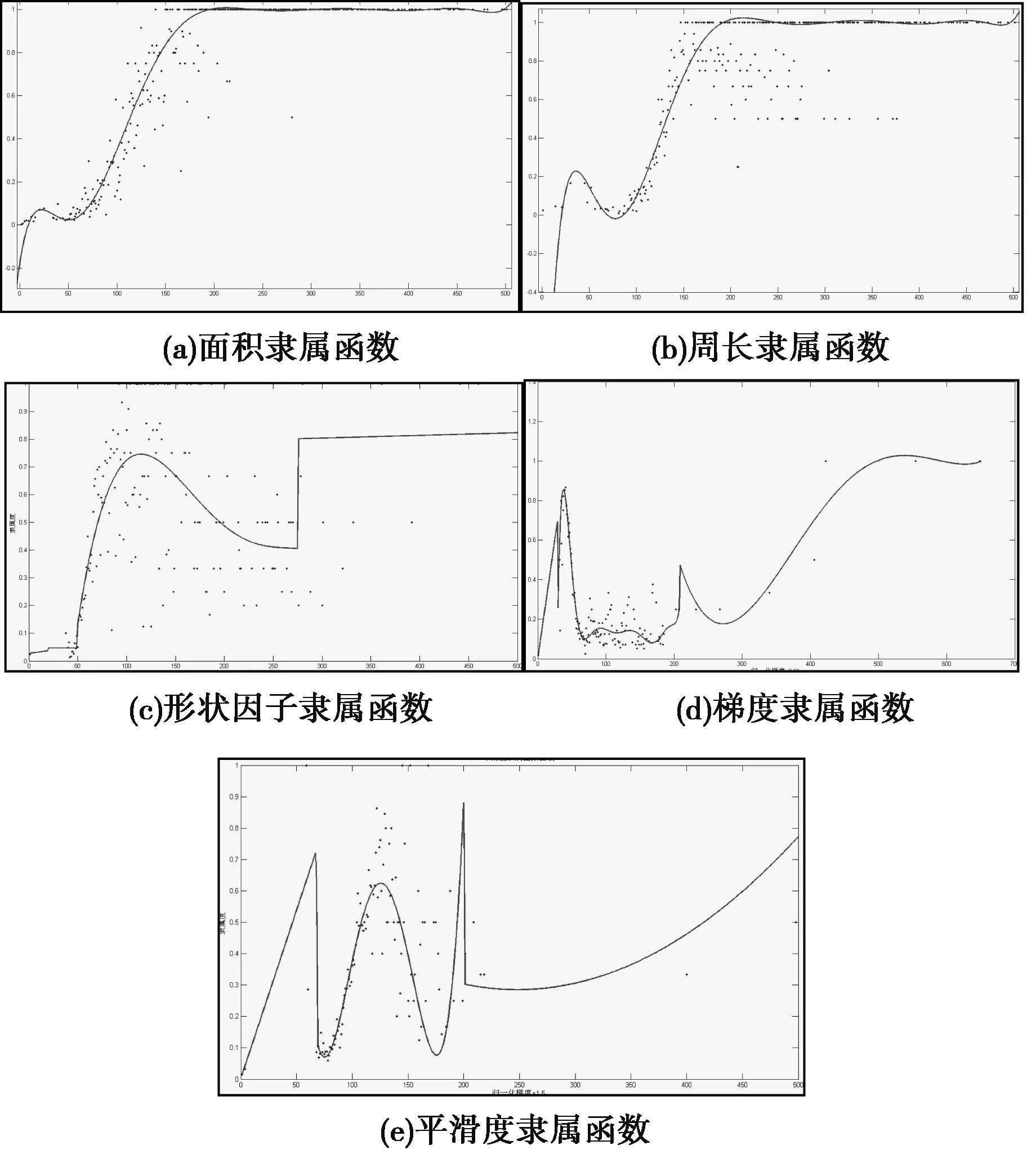
(a) Membership function of area(b) Membership function of perimeter (c) Membership function of shape factor (d) Membership function of gradient; and (e) Membership function of smoothness图6 矿岩块度区域特征的五种隶属函数Fig.6 Five membership functions of rock blocks
对于每一个岩石块度区域,当获取其参数后,都可以由隶属函数得到评价矩阵。然后再由评价矩阵和权重集来合成最终综合评价集。权重集由统计分析方法得出:
A=(0.4,0.2,0.2,0.1,0.1)各因素对应分别是:面积、周长、形状因子、梯度、平滑度。
3 试验结果及与其它算法的比较
3.1 模糊综合评判结果
针对初始分割后的图像,在进行模糊综合评判之前,首先要获取参数信息。然后取多幅图像进行分类分析,再利用标号和边界跟踪来获取每一岩石块度的面积、周长和形状因子参数,最后计算初始处理后的灰度图像中标号对应区域的梯度和平滑度参数,具体例子见图5(b)和对应的表2。所得到的参数先分别对其归一化和中心化处理后,然后再通过隶属函数来计算每个单独因素的隶属度,最后组合为评价矩阵。评价矩阵与权重集相乘后得最终评价集。
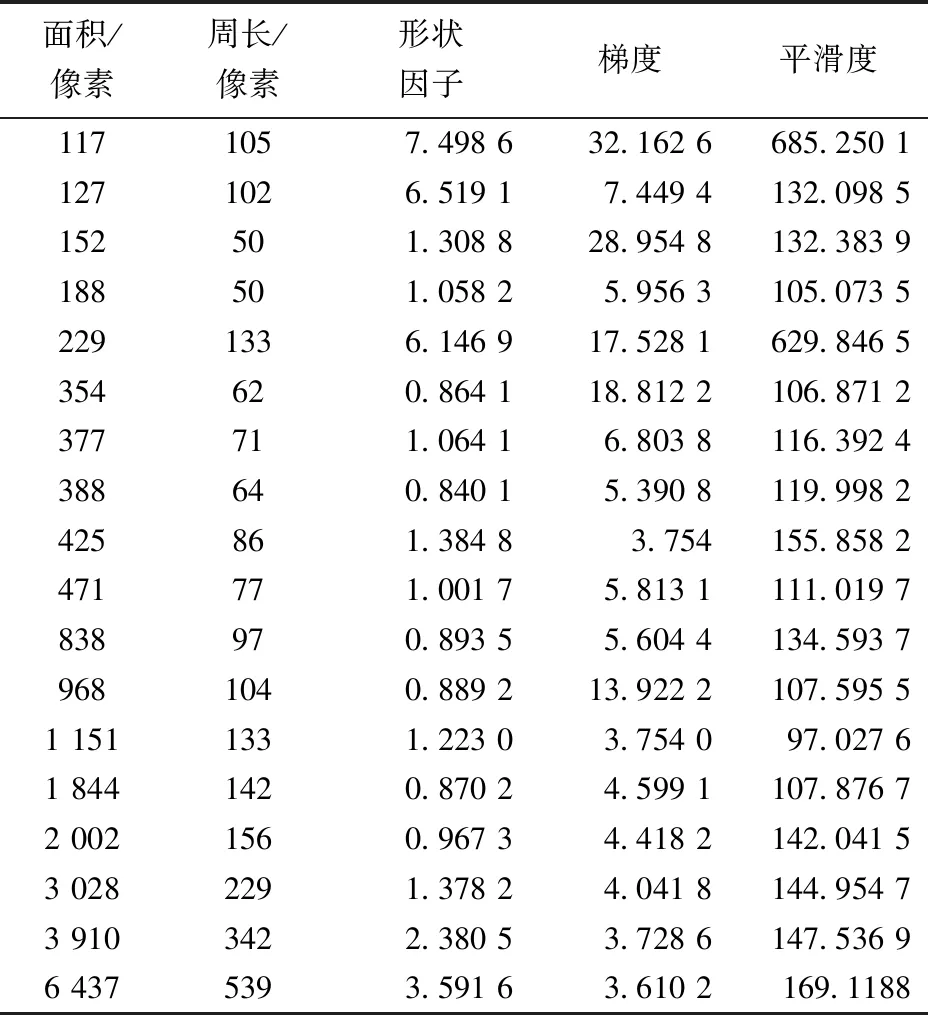
表2 最大类间方差法矿岩块度参数
以表2中两组矿岩块参数为例,做模糊综合评判。具体步骤如下:
1)因素集
(第一组数据)
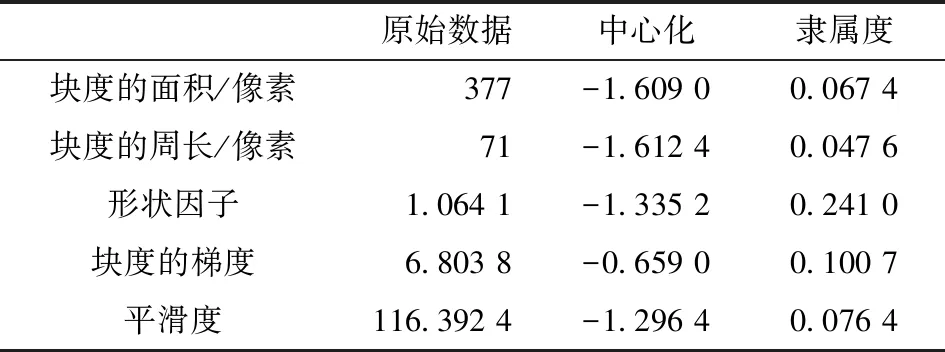
原始数据中心化隶属度块度的面积/像素377-1.609 00.067 4块度的周长/像素71-1.612 40.047 6形状因子1.064 1-1.335 20.241 0块度的梯度6.803 8-0.659 00.100 7平滑度116.392 4-1.296 40.076 4
(第二组数据)
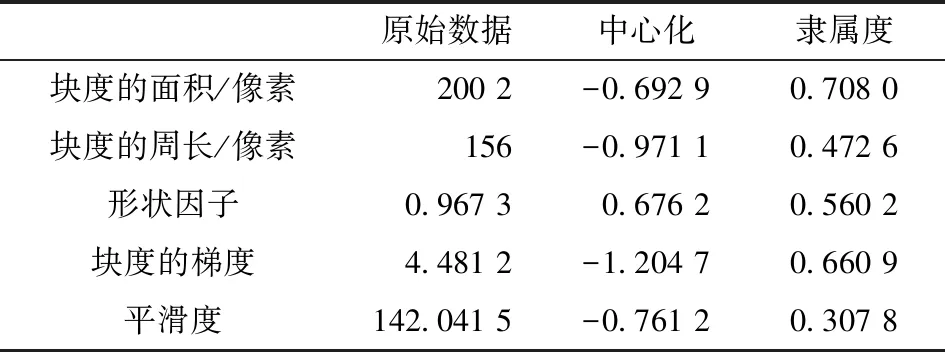
原始数据中心化隶属度块度的面积/像素200 2-0.692 9 0.708 0块度的周长/像素156-0.971 1 0.472 6形状因子0.967 30.676 2 0.560 2块度的梯度4.481 2-1.204 7 0.660 9平滑度142.041 5-0.761 2 0.307 8
2)评价矩阵
3)权重集
A=(0.4,0.2,0.2,0.1,0.1)
4)综合评价集:
B1=A*R1=(0.095 6 0.804 4);
B2=A*R2=(0.586 6 0.413 4)
根据最大隶属度原则,判定区域1不需要进一步分割。区域2需要进一步分割。
3.2 最终分割结果及与其它算法的比较
实验选取多幅图像进行,算法总体运行速度是复杂分割算法[1,13,15,19]的20倍以上(0.04秒/幅)。图7比较了人工筛选法、初始分割和自适应分割算法:相对于仅采用初始分割,自适应算法的分割结果与人工筛选的结果更为接近,更能精确地得到图像的矿岩块度,通过对100多幅矿石块度图像的实验及分析,新算法的分割结果准确率约为95%。新算法在初始分割基础上,对粘连的矿岩块度自动进行分离,分割的例子如图8所示。由图8和表3可看出,初始分割中矿岩块度之间的阴影部分(图中箭头所指出处)通过局部阈值分割,都分离开了,因此对阴影部分的分割效果较为显著。对所得到的分割结果进行统计分析表明:新算法与人工筛选结果接近。从图9中的5幅图像分割结果看出,几种最近研究热点的图像分割算法很难解决岩石块度粘连的难题。图9为新算法与其它两种类似的图像分割算法(聚类分析及图论最小割)[20]的比较情况,这里有四幅典型的矿岩块度图像。第一、二、三和四列分别是原始图像,聚类分析结果,图论最小割分割结果及新算法的分割结果,聚类分析的结果及图论最小割的结果,均以不同的颜色代表分割的块度。
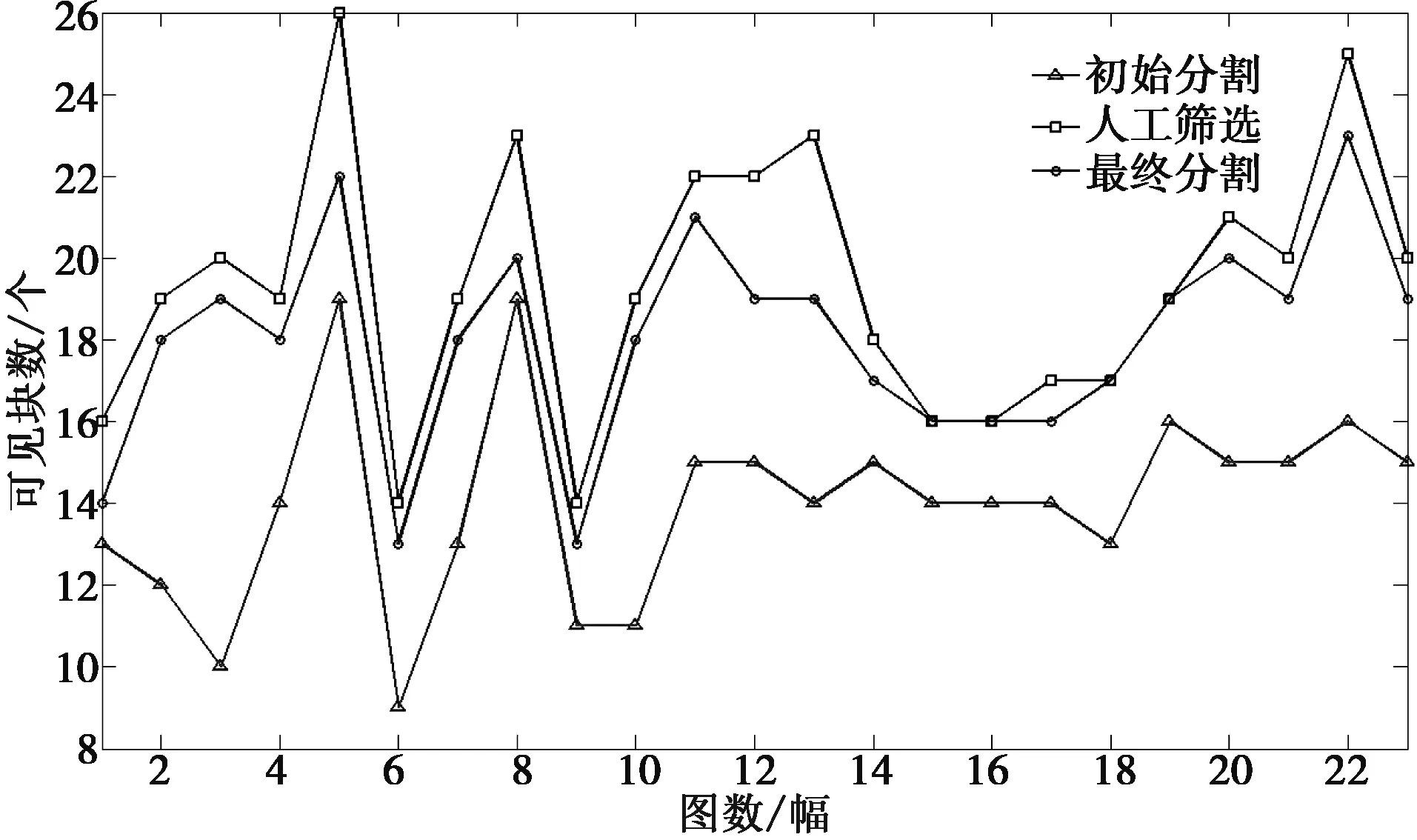
图7 人工筛选、初始分割、最终分割结果效果比较(上线为人工筛选结果,中线为最终结果,底线为初始分割结果)Fig.7 Artificial screening, initial segmentation results and final segmentation results
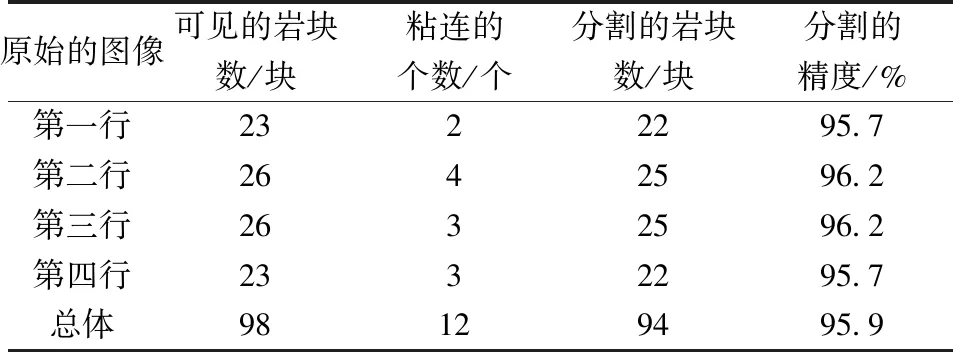
原始的图像可见的岩块数/块粘连的个数/个分割的岩块数/块分割的精度/%第一行2322295.7第二行2642596.2第三行2632596.2第四行2332295.7总体98129495.9
从图8~9中可以看出,聚类分析算法和图论最小割分割算法不仅仅处理时间较长(约为新算法的10~20倍), 而又达不到实际工程所需要的图像分割精度:对于该类矿石块度图像,除了粘连问题得不到解决外,而且还有欠分割的问题。

原始岩石块度图像 新算法的初分割结果 最终分割结果图8 新算法的初始阈值分割结果与最终分割结果Fig.8 Initial image segmentation results and final segmentation results of new algorithm

原始岩石块度图像 聚类分析分割结果 图论最小割分割结果 新算法分割结果图9 新算法和其它两种算法的分割结果Fig.9 Image segmentation results by using new algorithm and other two existing algorithms
4 结论
图像分割是矿岩块度在线检测系统中的关键技术,通常的全局阈值分割算法计算简单,运算速度快,稳定性较好,但难以解决粘连块体的问题。为了解决这一问题,本文研究了一种自适应式的阈值分割算法,该算法在对图像初始处理的基础上,应用Otsu全局阈值分割算法对图像进行分割。然后基于二值图像和灰度图像信息,利用矿岩块度特征参数根据模糊综合判断的结果对于未分割开的粘连岩块再进一步分离。实验结果显示:对于应用其它热点研究的三种图像分割算法(聚类分析和图论最小割),粘连的岩石块度很难被分割,而新算法是基于简单的Otsu全局阈值分割算法改进的,该方法图像分割的结果较好:精度95%以上,速度为其它算法的20倍以上,可以应用在矿岩块度的在线检测系统中。进一步的研究工作是考虑如何将该算法扩展应用到其它类似的复杂多目标物体(如颗粒)图像在线检测/监测系统中去。

