基于半参数Copula方法的蔬菜收入保险定价研究
赵玉
(东华理工大学经济与管理学院,江西 南昌 330013)
随着蔬菜种植面积的增加以及蔬菜流通体系的健全,蔬菜产业在提高农民收入、繁荣农村经济、优化农业产业结构方面的贡献越来越大。国内各地的“菜篮子工程”建设了大量的蔬菜基地、批发市场和集散中心,在丰富了居民菜篮子的同时,也加剧了蔬菜市场的竞争。由于蔬菜产品消费弹性低、上市集中且品种多、易腐烂、难储存等特征,使得蔬菜较其他农产品的价格波动更加剧烈。大起大落的蔬菜价格导致了市场的“蛛网震荡”,不仅仅损害了农民的利益,还造成了社会福利的耗散。为了稳定蔬菜供给,政府先后试点了各类蔬菜保险。相比期货、场外期权等专业的风险管理工具,农户利用保险管理市场风险不需要涉及专业的金融知识。而与订单生产相比,保险的违约风险和交易成本更低。美国在2014年出台的农业法案中调整了农业支持保护思路,取消了直接支付和反周期补贴,转而设立了价格损失保障和农业收入风险补助两个项目,加大了对农业风险管理项目的支持,更多地运用农业保险工具来保障农民的利益[1]。这对我国发展政策性保险制度具有很强的启示意义。从国际经验来看,政策性农业保险将成为我国农产品定价机制改革的重要手段,成为实现国家宏观和微观多重农业政策目标的重要途径[2]。
怎样借助政策性保险保障农户收益、促进农业发展是农业风险管理领域面临的难题。蔬菜不同于其他大宗农产品,可以探索开展价格保险[3]。但农产品价格指数保险要特别关注其可能的巨灾风险的分散机制,同质性很强的农产品可能并不适宜采用价格指数保险,对大部分农产品来说,收入保险或收益保险可能是更好的选择[4]。农产品收入保险可以弥补产量保险与价格保险存在的不足,更加符合农业生产者的风险保障需求[5]。与单独的农作物产量或者价格保险相比,农产品收入保险可以提高农户购买农业保险的积极性[6]。从社会福利角度分析,收入保险在增加生产者福利及整个社会福利方面比产量保险更好[7]。在实证研究中,有学者测算了粮食作物的收入保险费率。谢凤杰等[8]通过对辽宁省5个市县大豆收入保险费率进行测算,指出收入保险费率、保额存在明显地区差异。王保玲等[9]采用单产和价格测算了中国稻谷、小麦和玉米的收入保险费率。冯文丽和郭亚慧[10]测算了河北省玉米收入保险费率。经济作物保险方面,晁娜娜等[11]采用新疆棉花单产和收获期期货合约价格测算了不同保障水平下的棉花收入保险费率。刘素春和刘亚文[12]采用山东苹果批发市场价格数据测算了山东省苹果收入保险费率。徐婷婷等[13]厘定了陕西苹果收入保险的费率[13]。对比以上研究发现,收入保险费率的测算结果依赖于所使用的价格数据。目前学术界并未就价格数据选择标准形成共识。不同的数据选择标准和来源导致研究结果出现了较大差异,制约了农业收入保险的理论研究和实务发展。
收入保险可以为自然风险和市场风险提供双重保障,是未来我国农业保险发展的方向。从已有文献来看,国内外学者对蔬菜收入保险研究较少。从研究方法上来看,大多数研究采用了参数分布模型来拟合边缘密度,并采用单一Copula函数拟合联合分布,在缺少比较研究和模型选择标准时可能会造成保险费率测算的偏差。过高或过低的保险费率均不利于蔬菜收入保险业的发展。有必要采用较科学的计量方法测算蔬菜收入保险费率并与产量保险、价格保险做对比,为进一步优化我国蔬菜保险机制提出对策建议。
1 研究方法与数据来源
1.1 研究方法
由于可以很好的表述多个随机变量的联合分布,Copula概念由Sklar[14]提出之后,得到了广泛应用。假设价格和产量两个随机变量记为x1和x2,它们的边缘分布分别记作F1和F2,对应的概率值分别记作u1和u2,联合分布记作F,Copula函数记作C。F和C的表达式如下:
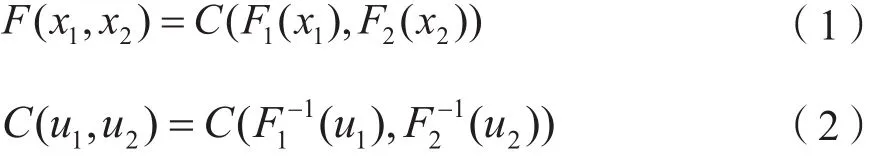
将联合密度函数记作f,Copula密度函数记作c,随机变量的边缘密度函数记作f1和f2。联合密度函数的表达式如下:
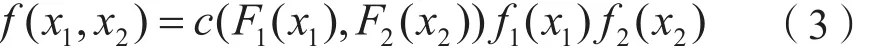
由此可得到收入的数学期望值μ的表达式:

将风险保障水平记作λ,保险合同的预期损失记作EL,其公式如下:
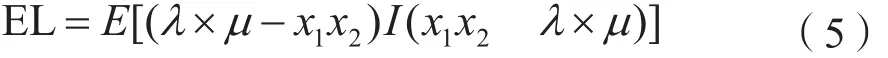
式中:E表示期望算子,I为示性函数,当实际收入x1x2小于保险金额λ×μ时,示性函数值等于1,否则等于0。收入保险的纯费率表达式如下:

同理可以推导出价格保险和产量保险的纯费率表达式。保险精算的难点在于选择合适的概率密度函数来逼近总体的真实分布。现有研究多采用拟合多个密度函数,然后根据K-S检验等统计方法进行优选。但这种方法依赖于事先对总体分布的假设,而做出这种假设往往会存在信息遗漏。非参数方法则不需要对总体分布做出先验假设。
从密度函数的定义可知,某一点x处的密度函数估计值的大小与该点附近所包含的样本点个数有关。若x附近样本点比较稠密,则密度值较大,反之,则较小。核密度估计法不依赖于样本区间的人为划分,该方法根据x邻域(窗口)内的点距离x的远近来确定它们对密度值的贡献大小。核密度法得到的密度函数估计值表达式如下:

核密度法容易受到窗口h大小的影响,h取值会影响到密度函数估计值的光滑程度。为了克服h取值的影响,将密度函数估计值和真实值的均方误差记作MSE(式(8)),求MSE的最小值,可以得到最佳窗口的估计值。

在采用非参数方法得到了边缘密度函数f(x)之后,采用极大似然法估计Copula函数的参数。价格和产量的联合分布函数为F(x1,x2,θ1,θ2,θ3),其中,θ1为x1的边缘分布函数的待估计参数,θ2为x2的边缘分布函数的待估计参数,θ3为Copula函数的待估计参数。价格和产量的联合密度函数如下:
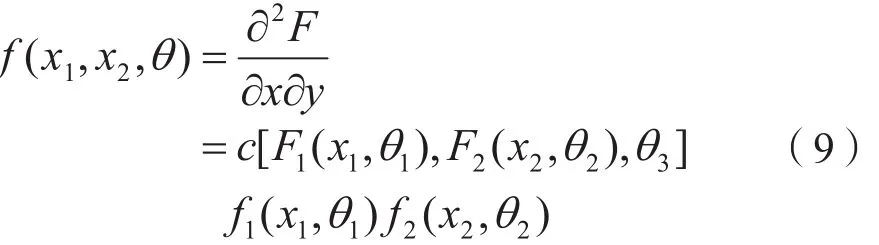
由于采用非参数方法估计了边缘密度函数,因此待估计的对数似然函数可以简化为:

常用的Copula函数主要包括正态Copula、t-Copula、Gumbel-Copula、Clayton-Copula和 Frank-Copula五种函数。分别计算不同类型Copula函数的极大似然对数值,可以选择出拟合效果最好的Copula函数。
采用非参数概率密度估计法测算价格因子和产量因子的边缘分布,构建半参数双风险因子的Copula模型并采用极大似然法估计出模型参数。采用Monte Carlo模拟获得单产、价格和收入的大样本数据,并计算出预期收入和不同保障水平下的纯风险费率。参考Cole和Gibson[15]的研究,模拟的步骤如下,首先根据合适的联合分布函数生成10 000组边缘分布函数F1和F2的值。其次,根据样条函数插值计算出对应的单产和价格数据。然后,将F1和F2的值代入联合分布函数中得到联合分布的概率,利用数值积分得到产量、价格和产量×价格的期望值。最后,利用式(5)和(6)厘定价格、产量和收入的纯保险费率。
1.2 数据来源与预处理
目前蔬菜保险试点地区采用蔬菜市场批发价格的均值作为保险设计的价格指数,但流通环节的价格包括了利润、运输成本和生鲜蔬菜的损耗等,无法准确反映蔬菜种植成本。只有采用与菜农直接相关的田边交易价格才能真实反映蔬菜的生产成本,更好地保障菜农的利益。本研究中所使用的价格为田边交易价格。数据使用了来自《中国农产品成本收益资料汇编》中对大中城市价格和单产的统计资料。本研究将大中城市种植范围广、居民消费量大的番茄、黄瓜、菜椒和白菜四种露地蔬菜作为研究对象,采用2004至2016年各大中城市蔬菜单产和价格数据。其中,涉及到种植番茄、黄瓜、菜椒和白菜的城市数量分别为19、20、24和23个。考虑到通胀会导致价格序列出现明显的趋势,采用蔬菜生产价格指数(定基指数,2004年为100)对蔬菜价格序列做了平减,计算出2004至2016年的实际价格。收入保险的关键是厘清产量和价格之间的联合分布。在此基础上,可以计算出不同保障水平下的保险费率。
由于保险合约需要满足可保性要求,即保险只保障不可预期的风险。因此在计算产量和价格风险的联合分布之前,先采用个体固定效应的面板自回归方法将各个城市的蔬菜产量和价格数据分解为序列趋势项、波动项和个体效应项。经验证,单产趋势方程和价格趋势方程中的自变量最优滞后阶数为1阶。从表1估计结果可知,方程拟合效果较好。趋势方程分解得到的个体效应反映了各城市之间的单产差异和价格差异,这种差异不随时间的变化而改变。
图1和图2表明,蔬菜单产高的地区对应的价格普遍偏低。计算番茄、黄瓜、菜椒和白菜四种蔬菜单产个体效应和价格个体效应的相关系数分别为-0.47,-0.56,-0.54和-0.80。虽然菜农种植蔬菜的收入风险主要来自价格波动,但在多数年份里,产量的变化对冲了一部分价格波动的负面影响。
目前的蔬菜保险主要分为产量险和价格险两类。由于收入等于产量与价格的乘积,因此,利用产量风险和价格风险之间“此消彼长”的联系来设计收入保险,既可以节约保险合约的交易费用,又可以保障农户的收入水平。另外,个体效应还反映出不同地区间产量或价格均存在着较大的差异,可以利用跨地区风险对冲优化蔬菜保险合约,降低保险费率。

表1 变量趋势方程估计结果Table 1 Estimation results of variable trend equations
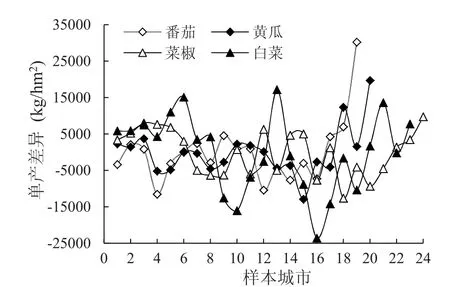
图1 蔬菜单产的个体效应Fig. 1 Individual effect of vegetable yield

图2 蔬菜价格的个体效应Fig. 2 Individual effect of vegetable price
2 保险费率的厘定
2.1 边缘概率密度函数估计
核密度函数有多种不同的表达式,不同的核函数对核密度估计影响不大。采用应用最广泛的正态核函数来估计产量波动和价格波动序列的边缘密度函数。由式(8)计算得到最优窗口宽度。其中番茄单产波动和价格波动序列的最优窗宽分别为146.32和0.08;黄瓜单产波动和价格波动序列的最优窗宽分别为138.90和0.06;菜椒单产和价格波动序列的最优窗宽分别为87.59和0.07;白菜单产波动和价格波动序列的最优窗口分别为136.85和0.04。将最优窗宽代入式(7)得到相应的四组边缘密度函数值。
图3报告了由非参数方法得到的密度函数形态。其中,番茄单产波动的最大值为39 693.90 kg/hm2,最小值为-33 972.75 kg/hm2,中位数为165.60 kg/hm2,峰度系数3.14接近正态分布的峰度,偏度系数0.22说明分布向右偏斜,番茄出现增产的概率大于减产概率。番茄价格波动的最大值为1.19元/kg,最小值为-0.69元/kg,中位数为-0.01元/kg,峰度系数3.05接近正态分布的峰度,偏度系数0.74说明分布向右偏斜,价格上涨的概率大于下跌的概率。黄瓜产量波动的最大值为65 599.20 kg/hm2,最小值为-28 092.90 kg/hm2,中位数为144.45 kg/hm2,峰度系数11.24表明与正态分布相比呈现尖峰后尾的形态,偏度系数1.54说明分布向右偏斜,黄瓜出现增产的概率大于减产概率。黄瓜价格波动最大值为1.30元/kg,最小值为-0.61元/kg,中位数为-0.02元/kg,峰度系数6.35表明与正态分布相比呈现尖峰后尾的形态,偏度系数1.49表明黄瓜未来出现涨价的概率大于跌价的概率。菜椒单产波动最大值为29 737.05 kg/hm2,最小值为-16 675.05 kg/hm2,中位数为-41.7 kg/hm2,峰度系数2.93接近正态分布的峰度,偏态系数0.65说明分布向右偏斜,菜椒未来出现增产的概率大于减产概率。菜椒价格波动最大值为0.96元/kg,最小值为-0.84元/kg,中位数为-0.03元/kg。峰度系数1.83表明分布较正态分布更为平缓,偏度系数为0.45表明菜椒未来出现涨价的概率大于跌价的概率。白菜产量波动最大值为55 814.10 kg/hm2,最小值为-34 007.40 kg/hm2,中位数为465.90 kg/hm2,峰度系数4.29说明与正态分布相比呈现尖峰后尾的形态,偏态系数0.45表明未来白菜增产概率大于减产概率。白菜价格波动最大值为1.84元/kg,最小值为-0.75元/kg,中位数为0,峰度系数27.14表明较正态分布更为陡峭,偏度系数2.98表明未来白菜涨价的概率大于跌价的概率。

图3 蔬菜单产和价格波动的边缘密度函数Fig. 3 Marginal density function of vegetable yield and price f uctuations
从图3的密度函数可知,四种蔬菜无论是单产还是价格,都呈现右偏态分布,并且单产波动幅度在45 000~90 000 kg/hm2之间,价格波动幅度在1.8元/kg至2.6元/kg之间。单产波动幅度由大到小依次为黄瓜、白菜、番茄和菜椒,价格波动幅度由大到小依次为白菜、黄瓜、番茄和菜椒。
2.2 联合分布函数估计
在估计边缘密度函数的基础上,由式(10)计算了Gaussian、Student-t、Frank、Clayton和Gumbel五种类型Copula函数的参数及对应的极大似然函数值。表2报告了联合分布估计结果。
由于Clayton 和Gumbel两种Copula函数的参数估计结果均不显著,故未在表中给出估计结果。在二元联合分布中,除Student-t型Copula函数包含两个参数外(参数1为相关系数,参数2为自由度),其他四种分布都仅含一个待估计参数。在Copula函数的基础上,计算了可以衡量单产波动和价格波动非线性关联程度的Kendall相关系数τ和Spearman相关系数r。这两个相关系数是设计保险合约的关键参数。
对比可知,四种蔬菜单产波动与价格波动的关联度并不相同。番茄单产波动和价格波动的负相关程度最弱,由产量风险对冲价格风险的效果并不理想。而白菜单产波动和价格的负相关程度最强,适合使用产量风险对冲价格风险。

表2 蔬菜单产波动及价格波动的联合分布估计结果Table 2 Estimation results of the joint distribution of vegetable yield and price f uctuations
2.3 保险费率厘定结果
在联合分布函数的基础上厘定三种类型保险的费率。首先根据极大似然函数值选择Student-t Copula作为随机数发生器模拟生成10 000组单产与价格波动值对应的概率。其次根据样条函数插值计算出对应的单产和价格波动数据。然后利用数值积分求得波动的期望值。最后利用趋势方程、个体效应、波动期望值和2015年的数据模拟出2016年蔬菜单产、价格和收入的期望值,通过与2016年实际数据相比,运用式(5)和(6)计算出不同保障水平下的纯保险费率。
表3报告了模拟计算得到的主要结果。其中,番茄的单产期望值为68 693.85 kg/hm2,目标价格为1.01元/kg,目标收入为67 732.80元/hm2。由于番茄价格波动和产量波动负相关性较低,导致在较高的保障水平下,收入保险的费率高于价格保险和产量保险的费率。保障水平小于75%时,收入保险的费率才逐渐低于价格保险的费率。黄瓜产量的期望值为63 430.50 kg/hm2,目标价格为0.88元/kg,目标收入为54 058.95元/hm2。菜椒产量的期望值为42 433.35 kg/hm2,目标价格为1.06元/kg,目标收入为43 530.45元/hm2。黄瓜和菜椒产量与价格风险对冲效果介于番茄和白菜之间。这两种蔬菜的收入保险费率低于价格保险费率但高于产量保险费率。
白菜产量的期望值为73 089.30 kg/hm2,目标价格为0.47元/kg,目标收入为29 752.80元/hm2。白菜价格波动和产量波动负相关性高,价格风险和单产风险对冲效果最好,其收入保险费率远低于价格保险费率,并且在大多数保障水平下也低于产量保险的费率。与其他三种蔬菜相比,由于白菜单产波动和价格波动均较高,在相同的保障水平下其产量险费率和价格险费率也高于其他三种蔬菜的相同险种。但由于白菜价格波动和产量波动负相关性最高,在相同的保障水平下,其收入保险的费率在三种蔬菜中最低。

表3 蔬菜不同险种的纯费率厘定结果(%)Table 3 Pure premiums of different types of vegetable insurance (%)
3 结论与讨论
3.1 主要结论
收入保险承担了产量保险和价格保险的双重功能。根据价格波动和产量波动“此消彼长”的负相关关系,可以优化保险合约,设计出费率更低的收入保险。借助个体固定效应的面板自回归模型将面板数据分解为趋势项、个体效应和波动项之后,采用半参数Copula方法模拟了价格波动和单产波动的联合分布并计算了不同险种的保险费率。研究得到以下几点结论:
第一,与其他Copula函数相比,t-Copula函数可以刻画波动项“尖峰厚尾”的形态,在拟合蔬菜产量波动和价格波动的联合分布时效果更好。
第二,蔬菜的产量波动和价格波动呈负相关关系,蔬菜的产量风险和价格风险可以部分对冲,对冲程度取决于两种风险的负向关联程度。
第三,蔬菜价格风险高于产量风险。对于产量波动和价格波动负相关性较弱的番茄等蔬菜可以采用价格保险,对于产量和价格负相关性较强的白菜、菜椒等蔬菜品种更适合采用收入保险保障农户利益。
3.2 讨论
目前国内主要试点了蔬菜价格保险而收入保险涉及较少。在实务方面,上海市针对白菜、生菜等蔬菜的价格保险保障水平为95%,费率为10%,价格触发依据为近三年批发市场均价;山东省针对白菜、大蒜等蔬菜的价格保险保障水平为75%,费率为10%,价格触发依据为平均生产价格;成都市针对本文中四种蔬菜的价格保障水平为保淡期的75%和保收期的90%,费率为保淡期7%和保收期的15%,价格触发依据为蔬菜离地价格;宁夏针对本文中四种蔬菜的价格保障水平为95%,费率为8%~10%,价格触发依据为田边交易价格[16]。在理论研究方面,尚未有针对国内城郊蔬菜收入保险费率厘定的相关文献,对比其他经济作物的研究结果,晁娜娜等[11]的研究表明目标成本为31 845元/hm2时,70%~90%的保障水平下,新疆棉花收入保险费率为3.37%~14.02%。刘素春和刘亚文[12]的研究认为在70%~90%保障水平范围内,山东省苹果的纯保费费率为19%~24.9%。徐婷婷等[13]的研究表明在70%~95%的保障水平下,陕西苹果收入保险纯费率在12%~19%之间。本文测算在蔬菜保险费率在70%~90%的保障水平下,番茄收入保险费率为7.97%~21.08%,价格保险费率为8.89%~19.12%;黄瓜收入保险费率为4.03%~14.41%,价格保险费率为6.42%~17.13%;菜椒收入保险费率为3.90%~13.04%,价格保险费率为4.00%~14.41%;白菜收入保险费率为1.45%~9.32%,价格保险费率为11.63%~22.39%。除番茄外,本文测算的大中城市蔬菜价格保险费率高于收入保险费率,也高于目前蔬菜主产区执行的保险费率。主要原因在于城郊蔬菜生产更接近零售市场,价格波动较蔬菜主产区更剧烈。另外一个原因在于目标价格设置不同。
保险费率除和保障水平有关外,还和收入(价格)的期望值有关。合理的收入或价格期望值既要满足可预期性,也要尽量覆盖生产成本。2016年大中城市番茄、黄瓜、菜椒和白菜的名义生产成本分别为77 533.95元/hm2、69 300.60元/hm2、54 331.95元/hm2、33 468.90元/hm2,以2004年为基期折算后的实际生产成本分别为33 813.30元/hm2、30 222.60元/hm2、23 694.75元/hm2和14 596.05元/hm2,实际生产成本占到期望值的50%~56%。为了避免引发逆选择和道德风险降低,保障水平在覆盖生产成本的前提下不宜设置过高。本研究测算的保险费率为各大中城市蔬菜保险的平均费率。不同城市蔬菜单产、价格以及相关收入存在着一定的差异。蔬菜经营风险在地域上的异质性可能会导致低风险区域相关保险市场供给充足而高风险区域的蔬菜种植业却得不到充分的保障。需要进一步研究如何通过农业保险产品和制度的创新来实现相关风险的空间分散或对冲。
4 对策建议
农产品收入保险具有双重保障和费率低的特点,是农业保险未来的发展方向。城郊蔬菜价格波动剧烈,既影响了农户的收入,也影响到市民的“菜篮子”。在分析蔬菜保险定价的基础上,为发挥蔬菜保险保障收入和稳定生产的作用,提出以下三点建议。
第一,做好田边价格的权威统计和及时发布。政策性农业保险具有准公共品的性质,在费率厘定方面,政府部门应加以指导并提供服务。目前国家统计局对城郊蔬菜田边交易价格的统计由国家农调队完成并按年度发布。较少的数据量不能很好地为保险精算提供支撑。一方面,农业部门应加大采样频率,并尽可能覆盖到城市周边更多的种植户。另一方面,发挥批发市场、远期市场等蔬菜市场的定价机制,向保险交易双方提供有效的价格信号。
第二,跨城市开展蔬菜收入保险。收入风险由产量因子和价格因子共同决定。蔬菜作为一种易腐农产品,主要由城郊菜农承担供给任务。对于时令蔬菜而言,各大中城市的价格差异较大,同时距离较远的地区气候因素差异也较大,可进一步在更大的空间尺度上对冲蔬菜收入风险。一方面,打破行政壁垒,鼓励跨区域开展保险业务。根据蔬菜品种量价的关系开发相应的蔬菜收入保险合约。另一方面,做好风险区划和巨灾风险的防范。科学量化不同城市之间蔬菜产量风险、价格风险的联系和传导路径。厘定极端风险给保险公司造成的损失,并制定相应的预案。
第三,重视菜农对蔬菜种植风险管理的诉求,对接蔬菜保险需求。农业保险政策效果不仅取决于对保险费率的精确厘定,还取决于农户对风险管理的诉求和需求。其一,应及时追踪调查菜农的相关诉求,在保险合约设计上尽可能地以农户需求为导向。其二,加强对农户、相关村镇干部的农业保险教育培训,提高农户和基层干部的保险意识,提升农户对保险条款、索赔和勘损等的认知水平。其三,加强农业保险理赔管理工作,鼓励合作社成立农业保险理赔的代理机构,降低保险理赔过程中的交易费用。

