两两比较模型的Why-not问题解释及排序∗

祁丹蕊,宋韶旭,2,3,王建民,2,3

1(清华大学 软件学院,北京 100084)

2(大数据系统软件国家工程实验室,北京 100084)

3(北京信息科学与技术国家研究中心,北京 100084)

1 引 言

1.1 问题背景

为什么科尔伯特不是总统?为什么Travelocity并没有告诉我Drake Hotel也是芝加哥可以作为备选的落脚点?为什么 Frank Sinatra没有棕色的眼睛?现实世界中,很多没有发生的事情都有非常明确的原因.了解为什么该发生的事情没有发生,是我们理解世界的正常方式.在数据库领域和软件系统领域,这种问题经常是这种形式:为什么这个程序是不完整的?为什么这个元组没有出现在查询的结果集?由于在用户得到结果之前需要对数据进行较多步骤的计算,所以这种问题的答案较难寻找.

数据起源,或者可以叫做一段数据的历史信息,曾经被用于研究解释数据从哪里来[1-3]和在原始数据变成结果集的过程中都发生了什么[4-7].对于这些信息的整合,可以帮助我们理解为什么某些元组并没有出现在结果集中[4,7,8].数据起源在这些工作中可以帮助人们解释一些结果集中非正常的结果.

对于数据库用户,一个常见的场景是这些编程人员被问为什么一条或者多条用户认为会有的数据并未出现在查询结果里.用户会猜想为什么.比如,一个查询的结果集是空的或者为什么同样的查询没有返回相同的结果值.当查询用来定义多视图的时候,用户可能会问为什么.例如,一个雇员的信息在雇员注册的视图和工资名单的视图中都没有.经常地,编程人员的第一反应是查看是否是查询本身的错误,比如条件太严格筛掉了部分可能结果,或者采用的 outer-join本来应该是 inner-join.然而,如果查询的表示方式是正确的,下一步编程人员要考虑的事情就是研究数据源,确定是否用户期望的结果数据真的在数据源中有出现.我们将这种形式的解释,即这种用数据来解释不在结果集中的元组的方式,叫做依赖数据的解释.在本文中,主要研究依赖数据的解释.

例1:考虑表1中的关系和查询Q1:

查询后的结果见表2.用户知道在查询结果中,应该有一个发射温度为78华氏度的飞机,时间顺序应是第12位,但是这个元组并没有出现在查询的结果集中.用户可能会问,为什么元组(6,78,12)没有出现?如果向原来的数据表插入元组(6,_,78,_,12),元组(6,78,12)就可以出现在查询结果集中,其中,“_”代表此属性可以取数据域中的任意值.我们根据观察表格发现,属性No.ETD和 Pressure都属于整数域,而如果用户也需要这两个属性值的一个合理推断,那么向原来的数据表插入元组(6,0,78,200,12)就可以看做是一个解释.若无法推断出精确属性值,否定某些可能的属性值,如向原来数据表中加入(6,¬2,78,200,12)也可以看做是一个合理的解释.

为了令没有出现在结果中的期望元组成为Q1的查询结果,枚举可能的缺失元组是一种可行的方案.但是在这些被枚举的可能中,存在着大量不合理的解释,通常违反唯一性约束或者源数据库内部的约束,如函数依赖和条件函数依赖.

利用数据库内部的约束可以初步约减一些不合理的解释,如文献[9-11]利用唯一性约束对得到的解释进行了约减,但在较大数据集上,利用数据库内部规则进行约减虽然有一定效果,但仍然会返回大量的解释(如文献[9]在本文中所使用的Airfoil Self-Noise上,在只有两个待修复属性的条件下,仍然返回37 856条解释),使得用户无法确认解释是否合理.

另外,在返回的解释中存在非常多利用变量表示的属性,即取属性域中的任意值均可.对于用户来说,此种解释的参考价值不大,所以生成用户可以理解的排序后的实例解释非常重要.

Table 1 Challenger USA space shuttle O-ring dataset表1 挑战者号美国航天飞机O型圈数据集

Table 2 Query results表2 查询结果

1.2 主要贡献

本文在以前工作的基础上,做出了如下主要贡献.

· 重新定义了Why-not问题解释的格式,使得呈献给用户的解释不含变量,使得解释更容易被理解;

· 在多属性的情况下,可能的值域会很大,为了避免数据稀疏性问题,提出将数据表示为两两比较关系,以{0,1}表示两个元组在某个属性上是否相等,从而支持更有效的概率模型学习;

· 利用统计方法计算两两关系概率分布,定义基于两两关系概率的支持度(support)与置信度(confidence),并根据这些度量对候选解释进行相应的筛选和排序;

· 利用分类和回归方法计算两两关系概率分布.统计方法在计算概率分布时未能充分考虑不同程度的属性关系.在分类和回归方法后,不同程度的属性间关系被考虑,使得最后返回的解释排序结果更加合理.结合回归方法并考虑不同程度的属性间关系后,我们提出了3种算法;

· 在不同数据集上的实验结果证明:利用统计、分类和回归方法计算两两关系概率分布的方法,可以为用户寻找Why-not问题的解释并返回较为高质量的解释.

1.3 论文结构

本文第 2节对相关工作进行具体介绍.第 3节给出本文的一些通用基础定义和问题的形式化定义.解释的统计学特征定义将与利用统计学方法寻找候选解释和它们的概率分布的算法一起在第4节中说明.第5节呈现结合机器学习分类方法的寻找候选解释及其概率分布的算法和3种结合回归方法寻找候选解释及其概率分布的算法.在第6节中将给出不同算法在真实数据集上的实验结果的比较.最后,在第7节中对本文的工作进行总结,并对未来的工作进行展望.

2 相关工作

2.1 Why-not问题

现今,数据量正在快速地增长.数据库管理系统从不同的数据源中抽取数据,聚合数据并将它们添加到数据库中.但是数据源常常不具有很好的质量.由于数据源的低质量和低一致性,用户或者数据科学家们经常会面临一种问题:当他们在一个数据库上执行查询的时候,一些他们期望的答案并没有出现在返回的查询结果中.继而用户可能会询问为什么一个或者多个元组没有在查询结果集中出现,也就是 Why-not问题.显然,为数据科学家或者用户提供针对于缺失元组的解释,可以帮助他们更好地理解或修复数据库.这种问题其实是数据起源问题的一个扩展,最早在文献[12]中被提出.

2.2 缺失答案解释

现今,已经有很多方法来解决简化数据转换分析问题,并使用户更容易理解和验证其行为和语义,包括数据沿袭[13]和更一般的数据来源[14]、子查询结果检查[15]、可视化[16]或转换规范简化[17].本文中提到的工作属于数据来源研究的范畴,重点是一个特定的子解决方案,旨在解释查询结果中的缺失答案,也就是解释为什么某些数据不存在.

缺失答案(MA)[10]在给出单个缺少的元组和单个选择项目连接(SPJ)查询后,计算基于实例的解释.事实上,它重写查询,使得重写查询的结果对应于指定的缺失答案的所有可能的基于实例的解释.基于实例的说明插入或更新源数据,并且可以通过信任表(属性)来减少需要被进行插入(更新)的数据.

Artemis[9]扩展了MA算法,使得它适用于一组涉及选择、投影、连接、联合和聚合(SPJUA查询)的非嵌套SQL查询.此外,可以指定多个缺失答案.计算的基于实例的解释描述了插入源数据的所有可能的方案,以便可以同时解释所有缺失答案.Artemis也考虑了修建解释的副作用.副作用在根据基于实例的解释更改源数据后,新增的结果除了指定的缺失答案之外,还会有其他的结果显示在查询的结果中.

Meliou等人统一了查询结果和缺失答案中存在数据的基于实例的解释[18].不使用数据来源[14],解决方案利用了因果关系和责任关系.此文详细研究了基于因果关系和责任的联合查询解释的复杂性,Meliou等人在文献[18]中还将现有数据的一种具体类型的解释统一为缺少数据的一种特定类型的解释.

Why-not[12]计算基于查询的解释.首先,给出一个缺失答案,它识别源数据库中包含常量值的元组,或者满足缺失答案的条件,而不是查询结果中的任何元组谱系的一部分[3].这些元组中的值称为兼容元组,通过查询运算符被跟踪,以识别哪些运算符将它们作为输入,而不是输出.在文献[12]中,该算法被证明适用于涉及选择,投影、连接和联合(SPJU查询)中的某一个查询.

NedExplain[19]类似于 Why-not,跟踪源数据库的元组,然而它不限制将兼容的元组限制到不是任何结果元组谱系的源元组.基于这种修改的基本假设和基于查询解释的新颖形式定义,NedExplain计算一个比Why- not更全面、正确和详细的解释集合,并支持涉及选择、投影、加入和聚合(SPJA查询)以及SPJA查询的联合.

ConQueR[20]输出基于修改的解释.给定一组缺失答案,SPJUA查询和源数据库,它首先确定产生缺失答案的必要源数据是否可用,这与Why-not类似.然后更改SQL查询,使得所有缺失答案成为输出的一部分,而副作用最小化.即在进行查询修改时,原始查询结果中存在的元组必须保留,只有最少数量的不是缺失答案的附加元组可以被允许出现在结果中.

最近已经提出了计算针对关系和SQL查询之外的查询基于修改的解释算法.在考虑副作用的同时,计算基于修改的解释的一种算法专门解答Why-not的Top-k查询问题[21].这个算法重点在于改变k或偏好权重,使缺失答案出现在查询结果中.Islam等人在文献[22]中提出了解决方案,回答了Why-not的反向Skyline查询问题.

2.3 条件函数依赖

此节将介绍条件函数依赖的基础定义[23]和它的一些有趣的统计学特征[24],即支持度和置信度.后文将基于条件函数依赖的统计学特征重新定义解释的统计学特征.

2.3.1 基础定义

一个在关系R上的条件函数依赖φ是一个元组R(X→Y,Tp),其中,

·X,Y是attr(R)中的一系列属性;

·R(X→Y)是一个标准函数依赖,又可以被叫做嵌在φ中的函数依赖;

·Tp是一个具有X和Y中所有属性的表,又可以被叫做φ的模式表,其中,对于每个元组t的任意的在X或Y中的属性A,t[A]为一个在dom(A)中的常数‘a’或者是一个未命名的变量‘_’.如果属性A在X和Y中都出现了,则我们用t[AL]和t[AR]来表示左边和和右边的A.当已知关系R时,我们将φ写为(X→Y,Tp).

关系R的一个实例I满足条件函数依赖φ,定义为,当且仅当对于实例I中的每对元组ti,tj,和条件函数依赖φ的模式表Tp中的每个元组,如果成立,那么成立.即:如果t1[X]和t2[Y]相等并且他们都与模式tc[Y]相配,那么t1[Y]和t2[Y]一定相等并且他们都与模式tc[Y]相配.此外,如果Σ是条件函数依赖的一个集合,我们说当且仅当对Σ中的每一个条件函数依赖φ,都有.

2.3.2 统计学特征

(1) 支持度

显然,经常一起出现的值有更多可能性是相关的,支持度就是基于这种思想的一种频率度量.关系R中的条件函数依赖φ=(X→A,tP)的支持度是R与φ相配的部分元组的数量占全部元组数量的比例,表示为support(φ,R),可定义为

其中,s是R中与φ相配的部分元组的数量,N是关系R中的元组数.

(2) 置信度

在很多情况下,有一些在支持度集中的元组在导因X处相同,但是在结果A处不相同.可以考虑每种不同的导因值单独地属于支持度集.可以将一个(完全实例化的)先行x作为一个组相关联的行集合,或者可以叫做“x组”.为了满足CFD,每个组中的所有行必须具有相同的结果值.

下面我们定义关系R的一个条件函数依赖的置信度:Cφ(R),它是可以保留的支持度集的最大分数,因此在删除所有其他行之后,支持度集的其余部分满足嵌入的函数依赖.

不失一般性,我们可以将关系R看做一个或多个行的集合ri=(xi,yi),其中,xi∈X是导因值,yi∈Y是结果值,并且其他的属性都不需要予以考虑.定义关系R中的总元组数为N.定义Nx为||ri:xi=x||,即具有相同导因值x的元组的个数(x组的大小),Nx,y为,并且定义R中φ的支持度集为sφ(R),即:

那么support(φ,R)也可以被同时定义为||sφ(R)||,那么:

2.4 利用两两比较方法寻找函数依赖

受利用两两比较方法寻找函数依赖的算法启发,我们简化了解决问题的统计学方法,并为与机器学习算法结合提供了可能.本节简略概述利用两两比较方法寻找函数依赖的3种算法.

传统寻找函数依赖的算法都是基于lattice的算法.Lopes等人提出的DEP-MINER[25]从有相同值的属性集中推断出所有最小的函数依赖.这些属性集被称为 agree集,它们的补集叫做 disagree集.Wyss等人提出的FASTFD算法[20]是DEP-MINER算法的一个改进.但是相似的是,FASTFD算法也是基于agree集来得到最小的函数依赖.在计算agree集之后,FASTFD采用了一种不同的策略,即计算disagree集来代替DEP-MINER中最慢的步骤.而在求agree集时,两种算法都需要将数据库中的元组进行一一对比来找具有相同值的属性集.

Flach和Savnik提出的FDEP算法[26]不同于前面提到的两种算法.FDEP算法成功地将数据库中的元组一一进行比较从而找到最小的函数依赖.

3 基础定义

为了方便对下文的理解,我们将阐述在整个论文中通用的一些基础定义,并给出相应的示例作为解释.

3.1 用户的问题

若给定数据库D,一个用户在数据库D上执行了查询query并且得到了一系列元组query[D]作为执行查询的答案.假设有一种情况,用户发现一些他期待会出现在答案里的元组并没有出现在答案中,用户可能就会问一个问题:为什么我期望的元组没有出现在答案中.例如,例 1中提到的问题“为什么元组(6,78,12)没有出现”,即可以称为一个用户问题.

3.2 基础定义

若给定一个数据库D,假设在数据库D中有x个关系,则将这x个关系记为T1,T2,…,Tx.对于每个在数据库D中的关系Tk,有mk个属性,可定义为A1,A2,...,Amk,则关系Tk可以记为Tk(A1,A2,...,Amk).若考虑将关系的下标和属性的下标综合起来,可以定义是第j个关系的第i个属性.对于每个Tk,假设有nk个元组在关系中,则这n个元组可被记为t1,t2, ...,tnk,若如前文所述与关系的下标结合,可以定义tij是第j个关系的第i个元组.

定义1(待调试场景).一个待调试场景S可以被定义成为具有3个元素的元组〈query,D,E〉.D的具体含义是上文中提到的原始数据库.query的具体含义是用户在原始数据库上执行的查询.E的具体含义代表了一个没有出现在query[D]但是出现在用户的问题中的元组.

例2:如例1中所示,此处待调试场景S就可以被表示成〈Q1,挑战者号美国航天飞机O型圈数据集,(6,78,12)〉.

定义2(缺失元组).一个消失元组可以被定义为元组d-tuple=〈d1,d2,…,db〉.值得注意的是,在d-tuple中的每一个属性值都应该为一个常量或者变量,其中,〈d1,d2,…,db〉代表用户在数据库D上进行查询后得到的结果的属性.

例3:如例1中例子提到,此处消失元组d-tuple=(6,78,12).

定义3(解释).若给定一个待调试场景S,一个解释可被定义为一个带符号的元组的集合,记为

例4:对于例1中的例子,元组(6,0,78,200,12)可以作为Why-not问题的一个合法解释,并且此解释未知属性全部为积极值.同时,元组(6,0,78,¬50,12)也可以作为另一种合法解释,其中有一个未知属性为消极值.更进一步,元组(6,¬0,78,¬50,12)仍然为一个合法解释,此处所有的未知属性都为消极值.

定义4(解释模板).若给定在数据库D上执行的查询Q,一个解释的解释式样可以被定义为从查询和消失元组中提取的需要被新加入原始数据库的元组有限集.

在Pattern(Rk)中,应是常量或者变量.对于一组确定的原始数据库D,查询query和消失元组d-tuple,有且只有一种解释式样.

从解释式样中可知,在Tk中的属性可以被分为两类:一类是已知属性,另一类是未知属性.假设Tk中的未知属性共有l个,则对于关系Tk,它可以被表示成.其中,代表未知属性,代表已知属性.

例5:对于例1,由于d-tuple=(6,78,12),分别对应例1数据集中的No.O-rings,Temp和Order属性,则此数据集的解释式样可以表示成为(6,N2,78,N3,12)

定义5(解释概率).一个解释的概率,或者说一个解释会被添加进原始数据库的概率,记为P(e),可以被定义为一种联合概率:

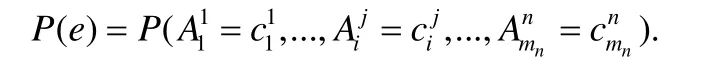
特别地,如果假设原始数据库中所有的关系都是独立的,即关系之间没有外键等关系,那么可以得到如下的解释概率表达式:

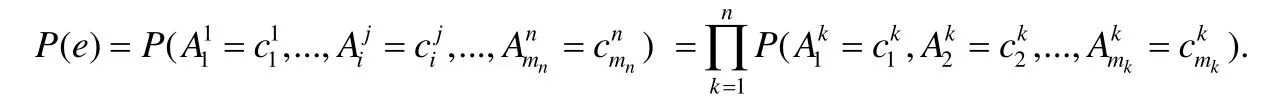
进一步地,如果假设原始数据库中所有关系的所有属性之间都是独立的,即属性之间没有类 FD或者 CFD的函数依赖限制,那么可以得到如下的解释概率表达式:

定义6(整体列表).解释的整体列表是一个由有顺序的元组组成的列表,记为,(e3,P(e3)),...}.其中,P(e1)>P(e2)>P(e3)>….

在整体列表Lall中,有一类比较特殊的解释,它们的特点是没有任何消极值.在整体列表中找到所有这样的解释并对他们进行排序,就可以得到解释的正列表.同理,也可以得到解释的负列表.

定义7(正列表).解释的正列表是一个由有顺序的元组组成的列表,记为,.其中,中无消极值

定义8(负列表).解释的正列表是一个由有顺序的元组组成的列表,记为,.其中,中无消极值

4 基于概率模型的解释排序

本节重点讨论利用基础的统计学方法寻找解释的两种算法:第 1种是未经任何变化从原始数据进行概率推理,第2种是在两两比较方法的基础上对数据进行概率推理.对于这两种算法,首先都会对算法整体进行概述,再详细解释算法并给出伪代码.为了便于理解,还会给出相应运算实例.

4.1 从原始数据进行概率推理

4.1.1 算法概述

给定原始数据,原始查询和用户在Aℓ+1,...,Am的Why-not问题,可以通过将未知属性的可能值进行分组,并通过古典概型和条件概率计算方式得到未知属性的不同可能值在已知属性的值已经得到的条件下出现的概率.对上述算法下的概率进行排序,即可以得到对未知属性的可能值(即解释的可能值)进行排序的结果,排序的结果从上到下可解释为解释的合理程度.

4.1.2 从原始数据进行概率推理算法

算法的输入值为原始数据库,用户在原始数据库上执行的查询和缺失答案,在接受输入后,算法主要执行以下步骤.

· 步骤1:统计所有属性值的联合概率.

首先,根据原始数据库中的数据进行分组统计.若对关系T(A1,…,Am)中的数据进行分组统计,那么对于关系T中的任意两个元组ti和tj,如果对于任意的属性Ak,都有ti[Ak]=tj[Ak],那么ti和tj即可以被分为一组.对于关系T分成的多个组,假设某个组中包含的元组数为num,相应的属性值分别为a1,…,am,关系T中的元组数为N,则:

· 步骤2:统计己知属性值的联合概率.

对于所有已知属性值,按照步骤1中描述的方法统计联合概率.首先,设所有已知属性的值为,即:对于关系T中的任意元组ti,如果对于任意的已知属性Ak,都有ti[Ak]=p[Ak],若以numknown代表已知属性的值等于p中已知属性值的元组个数,则其数量可以加1.则联合概率为:

· 步骤3:寻找候选解释.

由步骤2,我们得到了一组已知属性值全部相等的元组.但是它们的未知属性值可能不相等,这些不相等的未知属性值与已知属性值进行结合,就构成了候选的解释.

· 步骤4:计算不同候选解释在已知属性值条件下的概率.

从步骤2中得到的已知属性值全部相等的元组集合中,可以获得候选解释.这些候选解释也将这个集合分成了很多独立的组.在这些组里,任意两个元组的所有属性值全部相等.假设某一组中,所有未知属性的值为a1,...,aℓ,因此,

· 步骤5:排序概率,得到合理解释顺序.

对于所有不同的候选解释,经过上述的步骤,都可以得到在已知属性值条件下的条件概率.对得到的这些条件概率进行排序并返回这些解释,即为最后的结果.

在介绍了以上步骤后,给出算法的伪代码如下.

算法1.从原始数据进行概率推理.

输入:原始数据库中的关系T,查询Q,缺失答案q;

输出:整体列表Lall.

4.1.3 算法实例描述

例1中的Why-not问题中,未知属性为No.ETD和Pressure,若要从源数据进行概率推理,首先得到已知属性的值分别为

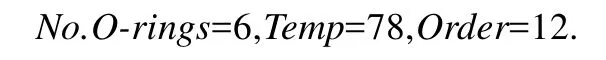
首先在表1中寻找是否有与 3个属性值完全相等的元组.寻找后发现没有找到,则从源数据进行概率推理的方法并不能给出一个合理的解释.即,寻找到的解释的准确率为0.

若此处找到了3个属性值完全相等的元组,则继续在这些元组中对于不同的No.ETD和Pressure的组合值进行分组,计算条件概率并排序,即可以得到最终的排好序的解释.

4.1.4 算法问题分析

上述算法最大的问题在于分组的步骤中,当数据集的数据量很大或者所有属性中有至少一个属性为键值时,分组的数量可能会非常多.由此带来的稀疏性问题会使得候选的解释非常少,或者候选解释的概率都非常小且差别不大,无法进行有效的排序以返回有意义的列表.

4.2 依据两两比较结果进行概率推理

4.2.1 算法概述

在此算法中,将利用两两比较的比较结果进行概率推理.对于源数据库中任意两个的元组,将他们的属性一一进行对比:若属性值相等,则记为1;否则记为0.将得到的结果组成一张新的两两比较结果表,利用此表和第4.1节中的方法,可以算出在两两比较结果表中解释的基本分布.参照CFD的支持度和置信度的定义,定义解释的支持度和置信度,并且通过对支持度的筛选,首先排除一些可能性非常小的解释,继而在支持度达到标准的解释中间寻找置信度符合标准的解释并排序,得到最终结果.

4.2.2 依据两两比较结果进行概率推理算法

算法的输入值为原始数据库,用户在原始数据库上执行的查询和缺失答案,在接受输入后,算法主要执行以下步骤.

· 步骤1:计算两两比较结果表.

首先根据原始数据库中的关系T(A1,…,Am)计算基于其的pari-wise比较表,记为S(B1,…,Bm).对于T中的任意两个元组ti和tj,若对于其中的某个属性Ak有ti[Ak]=tj[Ak],那么S中的元组tij[Bk]=1(表示T中ti和tj比较);否则,tij[Bk]=0.在将T中全部元组进行比后得到个元组,即S.

· 步骤2:根据两两比较结果表统计联合概率.

在得到两两比较结果表S后,按照第4.1节中统计所有属性联合概率的方法,可以初步统计所有属性的联合概率.假设两两比较结果表被分成了多个组,其中一个组对应的所有属性值为b1,b2,…,bm,包含的元组数为numb,则:

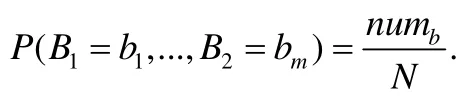
由于两两比较结果表S中全部为0/1值,所以将Why-not问题p中已知属性的值与原数据表进行对比,得到一张新的0/1表,其中的元组q1,…,qn是将Why-not问题p中己知属性的值与t1,…,tn中的已知属性值进行比较后得到的结果.

接着,计算两两比较结果表S中已知属性的联合概率,即计算Q中属性的联合概率,具体步骤类似于第 4.1节.在计算过Q中属性的联合概率后,对于任意的元组ti,有:

· 步骤3:对每个解释计算支持度和置信度.

解释的支持度和置信度是在对解释排序时需要采用的非常重要的评价指标.首先,仿照条件函数依赖,定义解释的支持度和置信度.

对于一个解释e,它的支持度被定义为

置信度被定义为

其中,对所有j=1,…,l,当e包含否定符号¬时,fe[Bj]=0;其余情况下,fe[Bj]=1.

· 步骤4:寻找候选解释.

从步骤3中得到所有解释的支持度以及置信度值后,需要根据支持度和置信度值筛选候选解释.在寻找候选解释时,我们允许用户提供一个阈值η,当解释的支持度值大于η时,此解释可作为一个候选解释.

对所有候选解释按照其置信度值进行排序,即可得到返回的整体列表.

在介绍了以上步骤后,给出算法的伪代码见算法2.

算法2.根据两两比较结果进行概率推理.

输入:两两比较结果表S,Why-not问题比较表Q,缺失答案q,阈值η;

输出:整体列表Lall.

4.2.3 算法实例描述

如例1中例子所示,首先,需要计算两张两两比较结果表,一张是表1中元组内部进行两两比较的结果表S,一张是Why-not问题中已知属性与表1中所有元组的已知属性值进行比较的结果Q.

首先,呈现如何计算S.以表1中的第1个元组和第2个元组为例,他们的No.O-rings和Pressure两个属性值相等,而其他的属性值不相等,则在S中即可以插入一条元组(1,0,0,1,0),仍分别对应表1中的5个属性.然后再以表1中的第1个元组和第3个元组为例,他们的No.O-rings,No.ETD和Pressure这3个属性值相等,则S中又可以插入一条元组(1,1,0,1,0).如此计算后,得到完整的S;再对属性的顺序进行重排,将未知属性放在前,已知属性放在后,即可得到最终的两两比较结果表S,表1的部分两两比较结果表见表3.

Table 3 Pair-wise table of Challenger USA space shuttle O-ring dataset表3 挑战者号美国航天飞机O型圈数据集的两两比较结果表

然后,呈现如何计算Q.以表1中的第1个元组为例,与Why-not问题中的No.O-rings,Temp,Order这3个属性值进行对比.他们的No.O-rings属性值相等,而其他的属性值不相等,则在Q中即可以插入一条元组(1,0,0),分别对应 No.O-rings,Temp,Order这 3个属性.然后再以表1中的第 2个元组为例,与 Why-not问题中的 No.O-rings,Temp,Order这3个属性值进行对比,No.O-rings属性值相等,而其他的属性值不相等,则在Q中又可以插入一条元组(1,0,0).如此计算后,得到完整的Q.表1与Why-not问题进行两两比较后的表见表4.

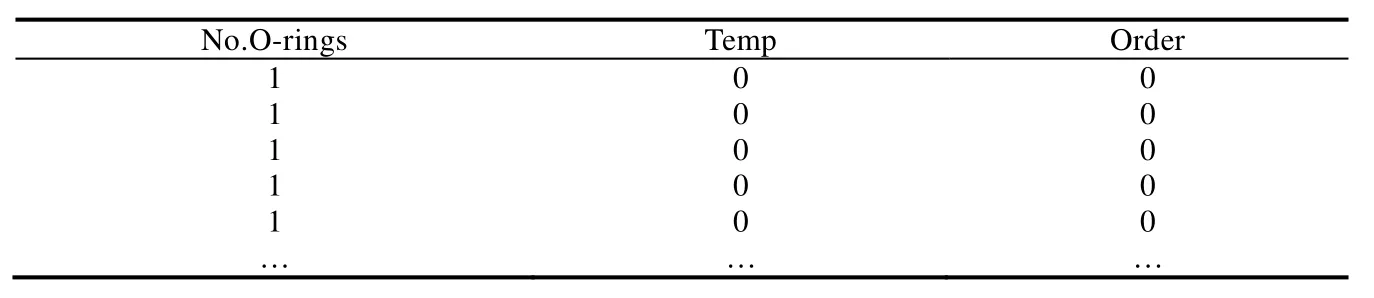
Table 4 Why-not pair-wise table of Challenger USA space shuttle O-ring dataset表4 挑战者号美国航天飞机O型圈数据集与Why-not问题的两两比较结果表

从表4中可以得到:

而从表3中可以得到:

继而,对每个候选解释,计算他们的支持度和置信度.在例 1中,候选解释(6,0,78,50,12),(6,1,78,50,12),(6,0,78,100,12),(6,1,78,200,12),(6,2,78,200,12),(6,0,78,200,12),再结合4种0,1值的可能组合,如对于(6,0,78,50,12),可衍生出(6,-0,78,50,12),(6,0,78,-50,12),(6,-0,78,-50,12)另外 3种候选解释,最终可以得到所有候选解释.根据支持度和置信度的定义,可得到如表5所示的针对每个解释的支持度和置信度值,筛选掉支持度小于等于 1的解释后,对置信度进行排序,即可得到解释的整体列表.

Table 5 Support and confidence表5 支持度和置信度

4.2.4 算法问题分析

上述算法的最大问题在于数据集很大时,不同的属性对最后得到的条件概率的贡献是不同的.若在中有一个属性非常明显地影响了其他属性,另外一个属性与其他属性都独立,显然,对于这个属性对结果没有什么贡献.而影响了其他属性,对最后得到的概率影响是巨大的.

5 概率模型学习

本节重点讨论将统计学方法的思想与机器学习的方法结合寻找解释.基于此思路,我们提出了两大类算法.

· 第1类算法是与分类结合的算法,用高级的多分类算法来预测联合概率;

· 第 2类算法是与回归结合的算法,在此类算法中,基于不同属性关系间的假设,我们提出了 3种不同的算法:第1种是简单地从已知属性值与未知属性值的回归式中进行概率推理;第2种是选定一个未知属性并将其余未知属性也作为回归的一部分,进行选定属性的概率推理;第 3种链式推理方法使每一个已求解出的未知属性值联合已知属性值作为即将要被求解的未知属性值的前提条件.

对于两类算法,首先都会对算法整体进行概述,再详细解释算法并给出代码.值得注意的是,上述算法全部基于第4节求出的两两比较结果表S.

5.1 分类

5.1.1 方法概述

对于两两比较结果表,可以将已知属性值作为特征,将未知属性值不同的 1/0组合看做不同的分类,利用较高级的多分类方法,比如 SVM,学习出一个关于已知属性值和未知属性值的分类模型.之后,对于这个学习出的分类模型,将第4节中提到的Why-not问题和源数据表进行对比后的对比表Q中的元组q1,…,qn一一代入分类模型中,得到不同条件下的属于不同分类的未知属性取值的概率.具体伪代码见算法3.

算法3.与分类方法结合.

输入:两两比较结果表S,Why-not问题对比表Q,Why-not问题q;

5.1.2 算法实例描述

由于与分类结合的方法和与回归结合的方法在求支持度值和置信度值的方法和第 4节相同,所以这些方法与前面的概率推理方法有区别的地方在于如何求取概率的步骤,实例中只说明到求取概率结束的步骤,剩余步骤方法与第4.2.3节中的方法相同.

在得到表3和表4之后,对于表3,可以将已知属性No.O-rings,Temp和Order在表3中的1/0值作为特征值,将未知属性No.ETD,Pressure的1/0组合值,即01,00,10,11作为4种类别,进行多分类操作.

在多分类操作之后,对于表4中的每一种元组值(表4中只有1种元组值),将其代入多分类结果的模型,即可得到如下的概率:

5.2 联合回归

在所有联合回归方法中,利用多元线性回归寻找属性之间的关系,完成分类的作用,并利用逻辑回归推理各个类别的概率.

5.2.1 回归方法简介

线性回归的最简单情景是只有一个纯量的预测变量x和一个纯量的结果变量y,这种线性回归被称为简单线性回归.扩展简单线性回归至多向量型的预测变量(记为X),即可称多元线性回归.在现实世界中的几乎所有用到线性回归的场景,都是多元线性回归.值得注意的是,在多元线性回归中,y仍然是纯量,但在多变量线性回归中,y可以是一个向量.

5.2.2 逻辑回归简介

在统计学中,逻辑回归是一个因变量有类别的回归模型,且因变量应为二元因变量,即只能取0值或者1值.二元逻辑回归模型通常被用来估计在一个或多个预测变量的条件下,二元因变量属于每一种分类的概率.逻辑回归中所用到的逻辑函数如下:

5.2.3 简单回归方法

简单回归方法的思想是:只考虑未知属性的分类在已知属性条件值下的概率值,不考虑未知属性之间的关系.即:假设未知属性和已知属性之间存在相关关系,但未知数属性之间彼此独立.所以简单回归方法分为如下步骤.

· 步骤1:对两两比较结果表S进行回归.

我们已知,未知属性在两两比较结果表中用B1,...,Bℓ表示,已知属性在两两比较结果表中用Bℓ+1,...,Bm表示.对于每一个未知属性,都可以通过多元线性回归找到其与已知属性的线性关系,即,对于每一个,都有:

· 步骤2:代入Q表中元组值,得到不同属性在不同条件下分类的概率值.

在得到每个未知属性和已知属性的线性关系后,将Q表中的元组qi(1≤i≤n)代入各个关系式中,得到每一个在qi取值条件下相应的Bj,将Bj取值代入逻辑函数,可得.

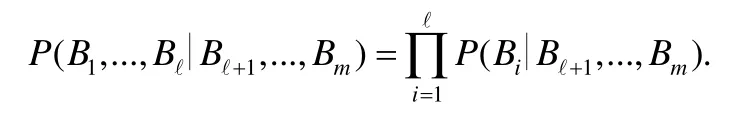
具体算法的伪代码见算法4.

算法4.简单回归方法.

输入:两两比较结果表S,Why-not问题对比表Q,Why-not问题q;

· 算法实例描述

对于例 1中的例子,在得到表3后,由于已知属性为 No.O-rings,Temp和 Order,未知属性为 No.ETD 和Pressure,则对于表3中的数据,将No.ETD那一列的数据,对所有已知属性列的数据做回归;对未知属性Pressure也执行同样的操作,可以得到:

对于表4中的每一种元组值(只有 1种元组值),将其代入回归结果的模型,可以得到No.ETD=0.60,Pressure=0.45.将两种值带入逻辑回归的式子中,即可求得:

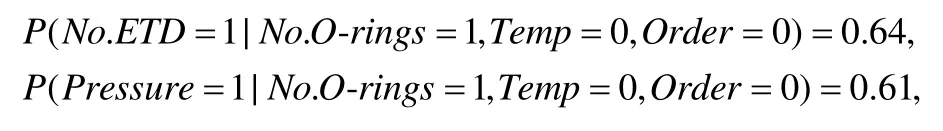
则:

同理,可以得到:

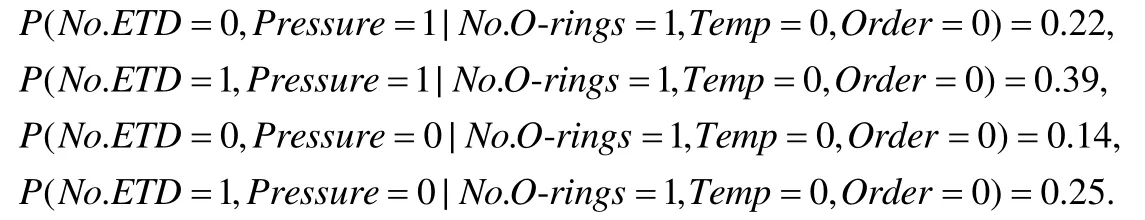
5.2.4 联合回归方法

此节中,介绍联合回归方法.联合回归方法的思想是,综合考虑某个未知属性在其他所有已知和未知属性的条件下的概率值.此方法考虑了未知属性之间的部分关系,即:假设未知属性和已知属性之间存在相关关系,且未知属性和未知属性之间也存在相关关系.所以,联合回归方法分为如下步骤.

· 步骤1:选取一个未知属性,对两两比较结果表S进行回归.

· 步骤2:代入Q表中元组值,得到不同属性在不同条件下分类的概率值.

在得到特定未知属性Bj和其他属性的线性关系后,将Q表中的元组qi(1≤i≤n)代入各个关系式中,得到在qi取值条件下相应的Bj,将Bj取值代入逻辑函数,可得:

具体算法的伪代码见算法5.

算法5.联合回归方法.

输入:两两比较结果表S,Why-not问题对比表Q,Why-not问题q;

· 算法实例描述

联合回归方法与简单回归方法在回归的步骤上不同.对于例 1中的例子,在得到表3后,由于已知属性为No.O-rings,Temp和Order,未知属性为No.ETD和Pressure,则对于表3中的数据,将No.ETD那一列的数据,对其他所有属性列(包含所有已知属性和未知属性)的数据做回归;对未知属性Pressure也执行同样的操作,可得:

对于表4中的每一种元组值(表4中只有1种元组值),将其代入回归结果的模型,可以得到:

解方程后得No.ETD=0.60,Pressure=0.45.将两种值带入逻辑回归的式子中,即可求得:

则:

同理,可以得到:

5.2.5 链式回归方法

链式回归方法的思想是,按顺序考虑未知属性的分类在已知属性条件值和已求出分类概率的未知属性值的条件下的概率值.此方法考虑未知属性之间的关系,即:假设未知属性和已知属性之间存在相关关系,且未知数属性和未知属性之间也存在相关关系.所以,链式回归方法分为如下步骤.

· 步骤1:选取一个未知属性,对两两比较结果表S进行回归.

我们已知,未知属性在两两比较结果表中用B1,...,Bℓ表示,已知属性在两两比较结果表中用Bℓ+1,...,Bm表示.若选定一个未知属性B1,都可以通过多元线性回归找到其与已知属性的线性关系,即:

· 步骤2:代入Q表中元组值,得到不同属性在不同条件下分类的概率值.

在得到特定未知属性B1和其他属性的线性关系后,将Q表中的元组qi(1≤i≤n)代入各个关系式中,得到在qi取值条件下相应的B1,将B1取值代入逻辑函数,可得P(B1=1|B[ℓ+1]=qi[Bℓ+1],...,B[m] =qi[Bm]).

· 步骤3:基于之前求过的未知属性和已知属性值求新的未知属性分类概率.

在得到特定未知属性B1和已知属性的线性关系后,假设下一步需要求另一特定未知属性B2的分类概率,首先执行步骤1,得到:

具体算法的伪代码如下.

算法6.链式回归方法.

输入:两两比较结果表S,Why-not问题对比表Q,Why-not问题q;

· 算法实例描述

链式回归方法与其他回归方法也是在回归的步骤上不同.对于例1中的例子,在得到表3后,由于已知属性为No.O-rings,Temp和Order,未知属性为No.ETD和Pressure,则对于表3中的数据,将No.ETD那一列的数据,先对所有已知属性列的数据做回归,可以得到:

对于表4中的每一种元组值(表4中只有1种元组值),将其代入回归结果的模型,可以得到No.ETD=0.60.继续将Pressure属性对包括No.ETD和所有已知属性列进行回归,可以得到:

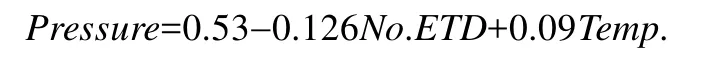
对于表4中的每一种元组值(表4中只有1种元组值),结合No.ETD=0.60将其代入回归结果的模型,可以得到Pressure=0.45,则:

同理,可以得到:

6 实验结果与分析

6.1 实验设置

6.1.1 使用数据集

本文的实验中,利用了UCI Machine Learning Repository中的Airfoil Self-Noise,SkillCraft1和WineQuality这3个数据集.具体信息参见表6.

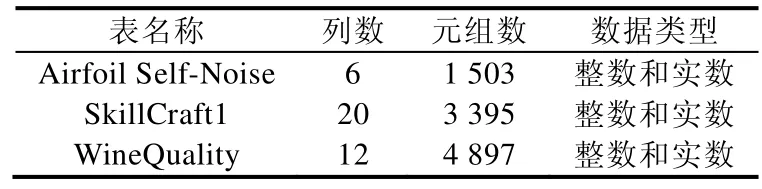
Table 6 Used datasets表6 使用数据集

值得注意的是:在本文的实验中,由于涉及到算法的中文名都较长,所以实验图例中采用不同算法名称的英文翻译的缩写,具体算法对应信息见表7.

Table 7 Algorithm names表7 算法对应名称

6.1.2 实验环境

本实验在以下环境中进行:处理器:2.5GHz Intel Core i7;内存:16GB 1600MHz DDR3;操作系统:MacOS 10.11.6;数据库系统:MySQL.

6.2 排序质量对比

6.2.1 数据集设置

在进行排序质量对比的实验时,首先在 3个不同的数据集上运行了本文中提到的两种不同的算法.而对于此实验,需要知道 3种不同数据集中的未知属性数和其数据类型,作为衡量数据集实验难度的标准.具体信息见表8.

Table 8 Dataset setting of experiment of ranking quality表8 排序质量实验数据集设置

6.2.2 质量衡量方法

本实验中,将最原始的数据集表格作为正确的参考值.不失一般性,对实验在每一个数据集上的查询都要进行100次实验,即:在每一次实验中,随机选取原始查询结果中出现的元组作为Why-not问题,并在源数据库中删除掉相应元组.然后,利用删除掉上述相应元组的数据库对Why-not问题进行解释,得到解释结果的正列表.对于每一种算法得到的解释结果的正列表,标记与被删除掉的源数据相同的元组出现的位置.在重复 100次实验后,选取top-1～top-100的位置,将这些位置中出现的正确元组数量相对于100次实验取均值,即可得到6种不同算法在不同数据集上的质量.

6.2.3 实验结果

由于在 3种数据集上,与多分类(SVM)结合的方法运行时间过长,不能得到可观的结果,故3种数据集上的质量曲线图中,只有除了与多分类(SVM)结合的方法之外的5种方法.

· Airfoil Self-Noise数据集

Airfoil Self-Noise数据集的6个属性中,只有两个属性为整数,其余均为实数.实验选取的未知属性也为实数属性.从图1(a)中可以看到:直接从原始数据进行概率推理的方法在 1 500条具有实数的数据中,已经显现出了数据域过大从而导致稀疏性的危害,即top-100中,命中的解释的个数为0.但当我们将过大的实数数据域通过两两比较压缩到{0,1}后再进行简单的概率推理,得到的结果就会比直接从原始数据进行概率推理好很多.当与简单的统计机器学习方法结合后,除了与多分类方法结合的算法运行过慢,与回归结合的 3种方法都在和两两比较概率推理差不多的时间内生成了结果,并得到了非常显著的准确率的提升.其中,联合回归方法在结果上稍优于简单回归方法,符合基础统计学理论.链式回归方法在 top-10的排序质量的表现上不如其他两种与回归结合的方法,主要原因是由于第2个计算的属性与最先计算的属性关联较弱,导致链式回归方法效果不明显.

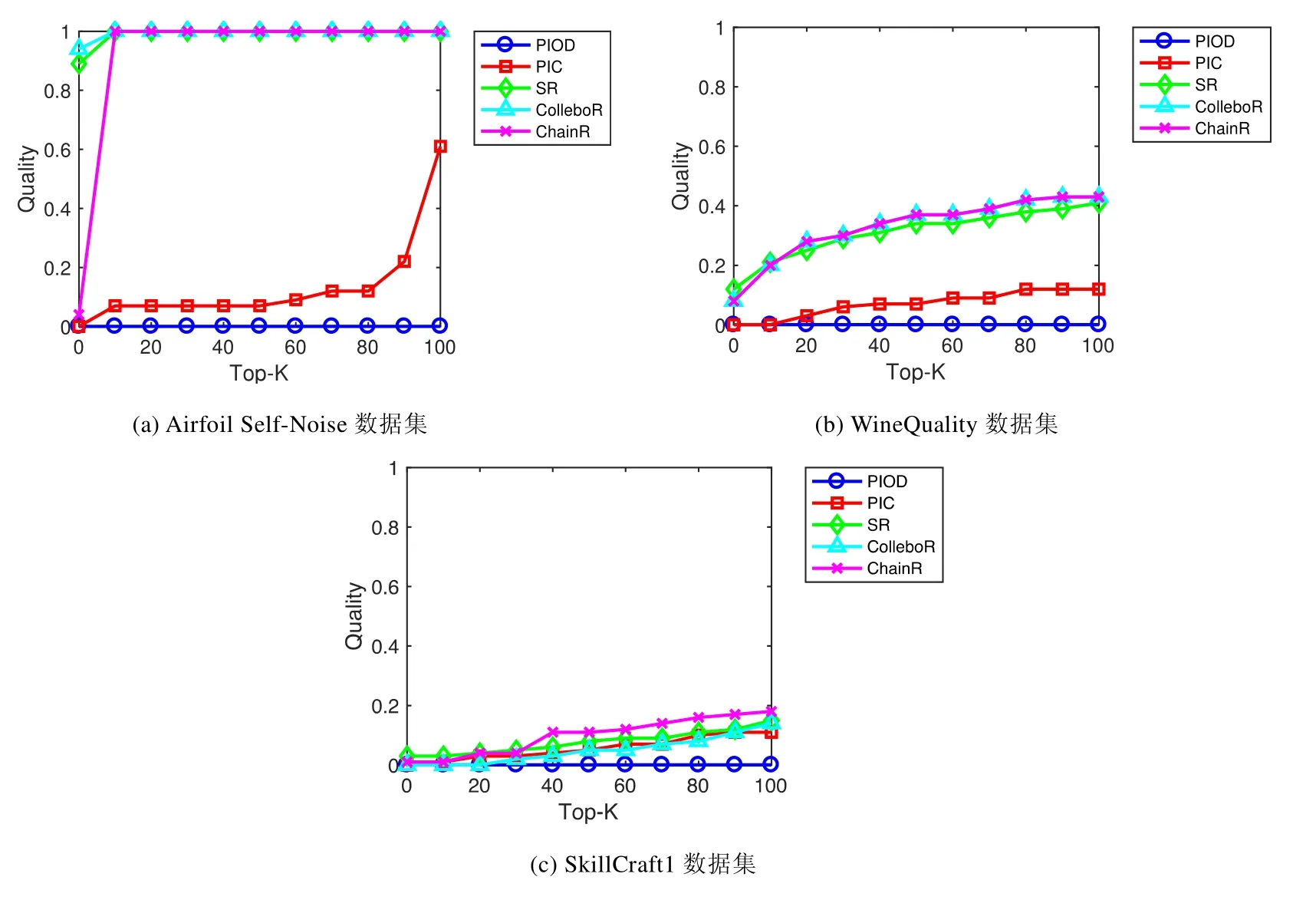
Fig.1 Top-100 ranking quality of all algorithms on three datasets图1 3个数据集上所有方法的top-100排序质量

· WineQulaity数据集

WineQuality数据集的12个属性全部为实数,即,WineQuality数据集其实是稀疏性很高的数据集.实验选取的未知属性也为实数属性.虽然只选取了两个位置属性,但从图1(b)中可以看到,直接从原始数据进行概率推理的方法在近5 000条具有实数的数据中,仍然由于数据域过大导致的稀疏性而毫无效果.即:top-100中,命中的解释的个数为 0.当我们将过大的实数数据域通过两两比较压缩到{0,1}后再进行简单的概率推理,得到的结果就比直接从原始数据进行概率推理好一些,但由于WineQuality本身是一个稀疏性相对于Airfoil Self-Noise数据集较大的数据集,从图1(b)中可以明显地看到,此方法相对于直接从原始数据进行概率推理的方法提升并不如图1(a)中明显.但当与简单的统计机器学习方法结合后,除了与多分类方法结合的算法运行过慢,与回归结合的3种方法都在两两比较概率推理一半左右的时间内生成了结果,并得到了非常显著的准确率的提升.其中,联合回归方法和链式回归方法在结果上稍优于简单回归方法,符合基础统计学理论.

· SkillCraft1数据集

为了验证与机器学习结合的方法在寻找稀疏性较低的属性时是否会由于求解最后结果的过程较为繁琐而导致效果不如简单的概率推理,我们在Skill Craft1数据集上选取了3个属性域较小的整数属性作为未知属性.从图1(c)中可以看到,直接从原始数据进行推理的方法仍然没有效果;但通过两两比较压缩到{0,1}后再进行简单的概率推理后,得到的结果就比直接从原始数据进行概率推理好一些.当与简单的统计机器学习方法结合后,除了与多分类方法结合的算法运行过慢,与回归结合的3种方法都得到了不比简单概率推理差、甚至稍好一点的排序质量.这说明对于稀疏性较低的属性,与回归结合的 3种方法在几乎相同的时间内,得到的质量并不会比简单概率推理差.

· 效果总结

综上,对 3个数据集上所有算法的排序质量分析可以看到,对于属性域较大、稀疏性较高的数据集,与机器学习结合方法的效果明显优于直接从原始数据进行概率推理和从两两比较结果进行概率推理的方法;而对于稀疏性较低的数据集,与机器学习结合的方法的效果也并不会弱于其他两种简单概率推理方法.

6.3 运行时间对比

在第6.2节排序质量对比的实验基础上,统计了每种方法在每个数据集上做100次实验后得到的平均运行时间,如图2所示.可以看到在实验过程中,数据集中的元组个数和属性个数对运行时间的影响都较大,所以在第6.4节中,基于WineQuality数据集进行扩展性实验的研究.

Fig.2 Runtime of all methods on three datasets图2 所有方法在3个数据集上的运行时间

6.4 扩展性实验

6.4.1 数据集设置

我们基于WineQuality数据集,做关于行扩展性和列扩展性的实验.

· 对于行扩展性实验,我们将提取 WineQuality数据集中 7个不同的子数据集,分别具有不同的元组数,而未知属性与第 6.2.3节全部相同,以衡量不同的元组数条件对不同方法求解 Why-not问题解释的排序质量的影响和对不同方法的运行时间的影响.具体信息见表9;

· 对于列扩展性,设置 5种不同数量的未知属性,以衡量在不同数量未知属性的条件下,不同方法求解Why-not问题解释的排序质量的变化趋势以及不同方法运行时间的变化趋势.具体信息见表10.

Table 9 Row scalability dataset setting表9 行扩展性使用数据集设置

Table 10 Column scalability dataset setting表10 列扩展性使用数据集设置

6.4.2 行扩展性

· 排序质量

为减少偶然性并全面观察各个算法排序质量随着元组数量的变化,在此实验中分别测量了在不同元组数条件下的top-1排序质量、top-10排序质量、top-50排序质量、top-100排序质量和top-300排序质量,具体结果如图3所示.

Fig.3 Top-1, Top-10, Top-50, Top-100, Top-300 quality under different number of tuples图3 不同元组数条件下的Top-1,Top-10,Top-50,Top-100,Top-300质量

从图3中可以看出:从原始数据进行概率推理的方法一直没有明显效果.而从图3(c)、图3(d)两张图中可以看出:依据两两比较结果进行概率推理的方法在top-50和top-100的排序质量有轻微随着元组数的增加而下降的趋势.但是图3(e)中明显可以得到下降的趋势.此实验结果与随着数据量增多,稀疏性增加,简单概率推理的效果下降的理论相符.

而对于3种与回归结合的概率推理方法,首先可以看到它们在5张排序质量图显示的结果上,因为3种与回归结合的概率推理方法充分考虑了属性之间的关系,所以得到的排序质量都优于两种概率推理方法,并且得到的排序质量一直很稳定,几乎不受数据量增加的影响.

· 运行时间

所有方法在不同元组数条件下的运行时间和内存消耗如图4所示,可以清楚地看到:从原始数据进行概率推理的方法仍然是最快的,但也是效果最差的.而 3种与回归结合的方法的图像表明,3种算法是随着数据集中元组数的增加呈线性增长的.依据两两比较结果进行概率推理的方法在元组数不断增加的条件下,运行时间呈非线性增长.若在相同的未知属性条件下,3种与回归结合的方法在时间和效果上都明显优于依据两两比较结果进行概率推理的方法.而在运行时的内存消耗方面,可以清楚地看到:从原始数据进行概率推理和根据两两比较进行概率推理的方法所占内存基本相同,而 3种与回归结合的方法的运行内存消耗顺序从小到大分别为简单回归方法、联合回归方法和链式回归方法.这种顺序是合理的,因为从简单回归方法到链式回归方法,属性之间的关系被更加详细地考虑,因此运行时所占内存联合回归方法和链式回归方法会大于简单回归方法.在元组数不断增加的条件下,5种方法的内存消耗也呈近平方式增长,与本文所使用的两两比较方式内存的增长速度相符.

Fig.4 Runtime and memory of all methods图4 所有方法在不同元组数条件下的运行时间和内存消耗

6.4.3 列扩展性

· 排序质量

为了减少偶然性并全面观察各个算法排序质量随着未知属性数量的变化,在此实验中分别测量了在不同元组数条件下的top-1排序质量、top-10排序质量、top-50排序质量、top-100排序质量和top-300排序质量,具体结果如图5所示.

从图5中可以看出,从原始数据进行概率推理的方法一直没有明显效果.而依据两两比较结果进行概率推理的方法随着未知属性数的增加,下降的趋势非常强烈;而在未知属性数超过4之后,此方法在top-300的质量也为0了.

而对于3种与回归结合的概率推理方法,首先可以看到:随着未知属性的增加,排序质量呈下降趋势.这是由于随着未知属性数量的增加,与回归结合的概率推理方法可以学习到的信息变少的缘故.但是由于充分考虑属性之间的关系,它们在top-1,top-10,top-50,top-100,top-300的排序质量上都优于两种概率推理方法.

Fig.5 Top-1, Top-10, Top-50, Top-100, Top-300 quality under different number of unknown attributes图5 不同未知属性数条件下的Top-1,Top-10,Top-50,Top-100,Top-300质量

· 运行时间

所有方法在不同元组数条件下的运行时间如图6所示,可以清楚地看到,从原始数据进行概率推理的方法仍然是最快的,因为从原始数据进行概率推理的方法在计算时不需要进行两两比较等一系列步骤,但是也是效果最差的.而 3种与回归结合的方法的图像表明,3种算法是随着测试数据集中未知属性数的增加呈线性增长的.依据两两比较结果进行概率推理的方法,在未知属性数不断增加的条件下,运行时间仍然稳定,几乎不受未知属性数的影响.因为在两两比较时,未知属性数的数量相对于元组数量对运行时间的影响较小.

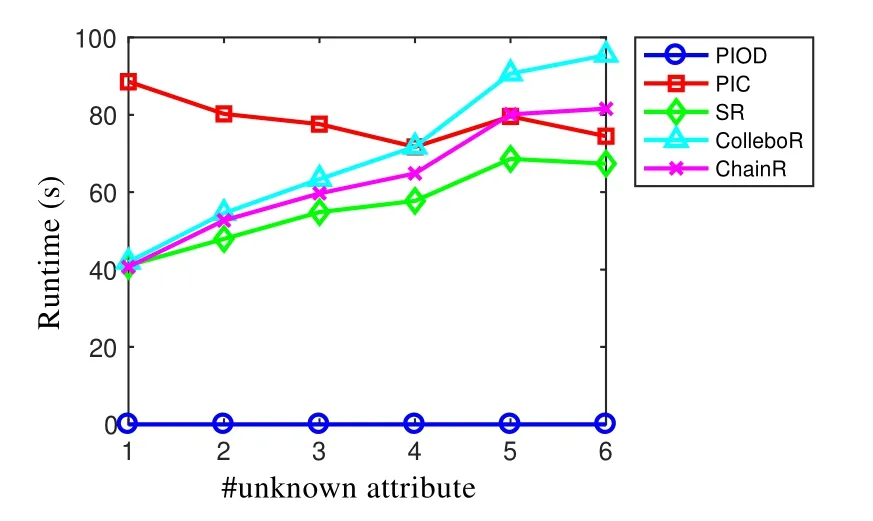
Fig.6 Runtime of all methods under different number of unknown attributes图6 所有方法在不同未知属性数条件下的运行时间

6.4.4 列扩展性(含与分类结合方法)

为了比较与分类结合的方法和其他方法在不同未知属性数条件下的效果,我们利用WineQuality数据集的子数据集WineQuality-300来对6种方法做不同的对比实验.WineQuality-300中含有300条数据,用如此少量数据的原因,是因为多分类方法的时间效率过慢,用太大的数据集无法在可观时间内得到结果.

在此列扩展性实验中,仍然将排序质量和运行时间作为两个重要的指标.为了更详细地看到每个算法在top-50之前和top-100之前的变化趋势,此实验中还画出了在不同未知属性数条件下,top-50前和top-100前的趋势图.

· 排序质量

所有方法在不同未知属性数条件下,Top-1,Top-10,Top-50,Top-100,Top-300的排序质量图如图7所示(含与分类结合的方法).在图中可以清楚看到:当在Top-1,未知属性个数为1时,如图7(a)所示,与分类结合的方法比其他的方法得到的结果要好一些;但在其他情况下,如图7(b)～图7(e)所示,与分类结合的方法得到的排序质量并没有相对其他的方法有显著的提升.这是由于在未知属性个数为 1时,分类时问题为二分类;而当未知属性个数为2时,分类问题变为四分类,以此类推.所以当未知属性个数增多时,由于类别个数呈指数增长,与分类结合的方法效果并不会相对其他方法有显著的提高.

Fig.7 Top-1, Top-10, Top-50, Top-100, Top-300 quality under different number of unknown attributes图7 不同未知属性数条件下的Top-1,Top-10,Top-50,Top-100,Top-300质量

为了更加详细地研究与分类结合的方法和其他算法的效果对比,在下文中给出每个算法在 top-50之前和top-100之前的变化趋势图.

· Top-50排序质量趋势

所有算法在 top-50之前在不同属性数条件下的变化趋势图如图8所示(含与分类结合的方法).图8(a)～图8(f)分别代表了未知属性数为1～6时,各个算法的top-50排序质量趋势.从图中可以看出,直接从源数据进行概率推理的方法仍然是最差的.而依据两两比较比较结果进行概率推理的方法在所有属性数条件下都差于与机器学习结合的方法.与分类结合的方法在前top-10的表现比与回归结合的方法好,而在top-10之后都差于或持平与回归结合的方法.

Fig.8 Top-50 quality ranking trend under different number of unknown attributes图8 不同未知属性数条件下的Top-50排序质量趋势

· Top-100排序质量趋势

所有算法在top-100之前在不同属性数条件下的变化趋势图如图9所示(含与分类结合方法).图9(a)～图9(f)分别代表了未知属性数为1～6时,各个算法的top-100排序质量趋势.Top-100排序质量趋势图是对top-50趋势图做了扩展,以防止因为取的top-k数量过小而导致趋势不明.观察图9,得到的结论与top-50趋势图得到的结论一致.

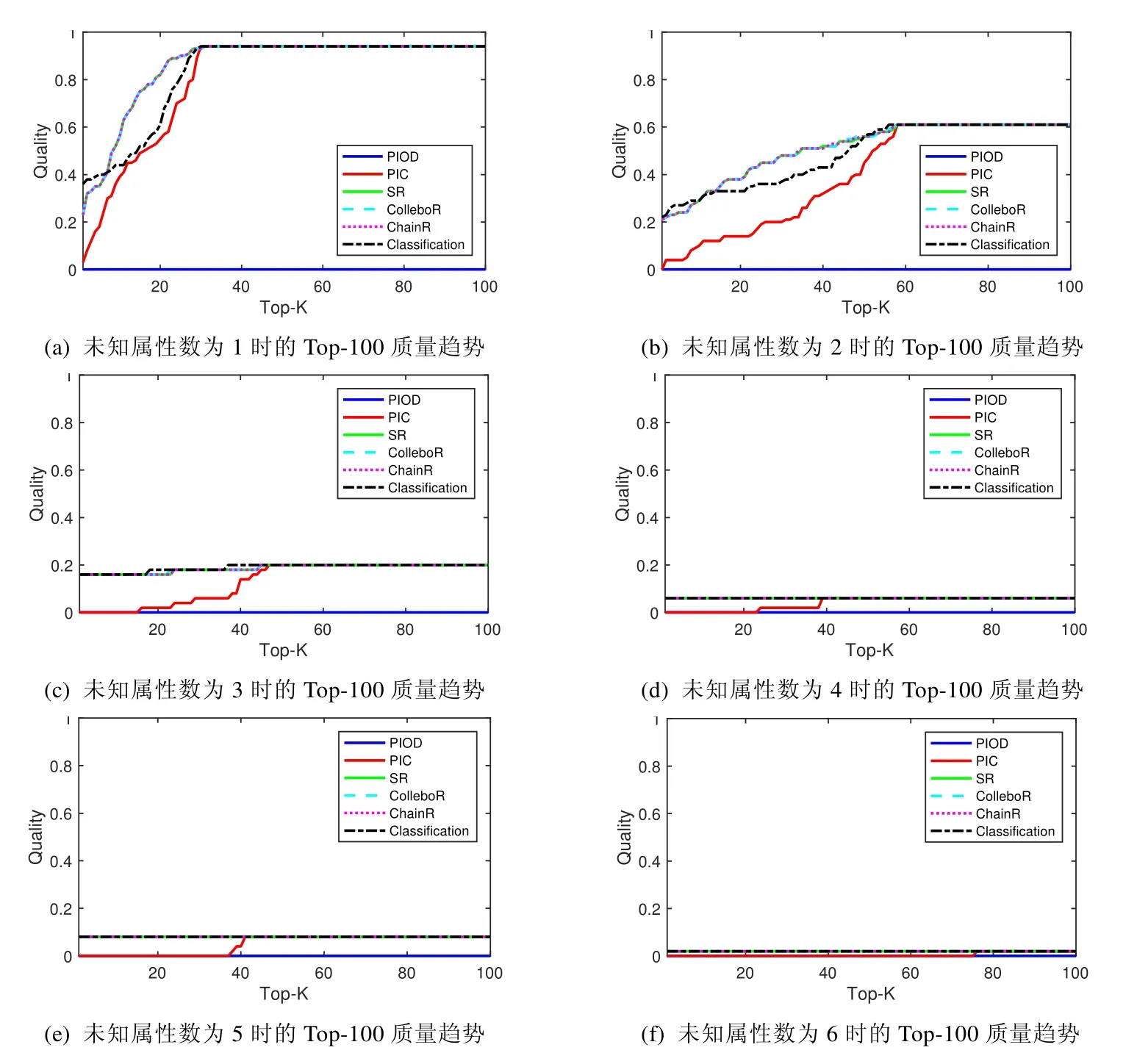
Fig.9 Top-100 quality ranking trend under different number of unknown attributes图9 不同未知属性数条件下的Top-100排序质量趋势

· 运行时间

所有方法在不同未知属性条件数下的运行时间如图10所示(含与分类结合方法).可以明显地看出:与分类结合的方法效率非常低,而其他方法的运行时间都明显优于与分类结合的方法.

Fig.10 Runtime of all methods under different number of unknown attributes图10 所有方法在不同未知属性数条件下的运行时间

6.5 讨 论

在寻求 Why-not问题解释的应用场景中,有的应用场景对响应时间要求较高,如对 NBA球星信息的查询;有的场景对解释的准确率要求较高,如用户在查询某个公司的员工信息时,对缺失的年龄、社保号等信息的Why-not问题解释准确率要求较高,甚至是绝对准确.所以根据不同的应用场景,基于两两比较模型的 Why-not问题解释及排序方法更适用于对解释准确率要求较高的场景.

7 结论与未来工作

7.1 结 论

本文受利用两两比较方法寻找函数依赖的算法启发,提出了将两两比较方法和统计学方法以及机器学习方法进行结合的针对 Why-not问题寻找解释并对解释进行排序的算法.在寻找解释之前,对传统解释的形式进行了重新定义.对于取值域非常大的属性,提出利用两两比较方法将属性的值域压缩到{0,1},并首先利用统计学方法对得到的两两比较结果值进行初始统计,得到一种候选解释和其概率,计算统计学特征后进行排序.之后,和机器学习中的多分类和回归方法进行结合,经过实验证明,与回归方法结合较与多分类结合方法更为有效;与多分类结合的方法比直接进行概率统计的方法更为有效.

与之前已有的成果相比,本文更多地考虑了在求解释的过程中对解释进行详细化和排序,是在以前的相关工作中并未被仔细考虑的方面.实验证明:详细化和排序确实对用户更好更快地寻找解释起到了积极作用.

7.2 未来工作展望

在后续工作中,可以从两个个方面对现有工作进行扩展.

· 首先,考虑更大规模的数据.目前,我们利用两两比较方法寻找解释并对解释进行排序的时候,考虑的是整个数据库中的对比结果.而在后续工作中,可以考虑对原始数据集进行适当采样,使得采样结果可以大致描述整个数据集的样子.然后,在采样结果上进行两两比较的操作与运算;

· 其次,可以考虑频繁更改的数据库.现有的工作只针对于确定的数据库,对于频繁更改的数据库,可以考虑在数据库的时间切片上进行采样,并利用某个时间窗内找到的可能解释,综合解释的时间戳,找到最合理的解释.

综上所述,上述两方面将是日后研究的重点.在将来的工作中,将争取对现有工作进行扩展,得到能够解决更加通用的实际问题的方法.