二维非稳态对流扩散边界控制问题的简化算法
张国平 罗贤兵

摘 要 针对二维非稳态对流扩散边界控制问题计算量大的问题, 提出了基于降阶模型的最优实时控制方法. 利用POD(the Proper Orthogonal Decomposition)和奇异值分解以及Galerkin投影方法得到了具有高精度离散形式的状态空间降阶模型. 在所得的降阶状态空间模型中, 利用离散时间线性二次调节器方法设计出了最优控制器. 对流-扩散过程的控制模拟结果说明了所提方法的有效性和准确性.
关键词 对流扩散边界控制问题; 特征正交分解(POD); 奇异值分解; 降维模型
中图分类号 0242.1 文献标识码 A
Abstract Boundary control of two-dimensional unsteady convection diffusion is a large-scale optimization problem, and an approach was presented for optimal control based on reduced-order model, which was derived from a discrete-time low-order state-space model with high accuracy by using POD(the Proper Orthogonal Decomposition), singular value decomposition (SVD)and Galerkin projection. Optimal controllers were designed based on the low-order state-space models using discrete-time linear quadratic regulator (LQR) techniques. The controlling simulation results in the convection-diffusion process illustrate the effectiveness and accuracy of the proposed method.
Key words convection-diffusion boundary control problem; the Proper Orthogonal Decomposition (POD);singular value decomposition; dimensionality reduction model
1 引 言
對流扩散方程所描述的最优控制问题[1]广泛应用于许多领域, 如:大气污染控制问题, 流体控制问题等, 所以寻找稳定、高速实用的数值方法[2], 有着非常重要的实际意义. 目前常用有限差分法[3]
和有限元法[4]解决此类问题, 然而一般情况下, 大多数的差分格式和有限元格式计算量比较大, 而且占用计算机内存多, 特别是对于高阶的离散系统, 其计算量将呈指数规律增长, 计算成本将变得很大. 因此, 现在重要的问题是如何简化计算,减少计算时间和内存容量,并确保解具有足够的精确性.基于矩阵奇异值分解的特征正交方法(Proper Orthogonal Decomposition)能提供具有足够高精度而自由度又较小的低阶模型, 简化计算,节省CPU和内存.
文中所介绍的特征正交分解方法[5]主要是提供一种有效逼近大量数据的最优逼近方法, 它的实质是在最小二乘意义下[6]找寻能代表已知数据的一组正交基.即一种求已知数据的最优逼近方法. 此外,由于POD方法是在最小二乘意义下最优的,所以该方法有完全依赖数据而不对数据作任何先验假设的优点. 在文献[7]中以对流扩散反应过程为例,设计了基于低阶模型的线性二次调节器的最优控制[7], 将离散空间模型的阶数大大地降低了, 其仿真实现了最优反馈控制的实时应用, 但是没有对二维对流扩散方程描述的系统实现最优控制.
本文将特征正交分解应用于二维非稳态对流扩散边界控制问题, 在文献[7]的基础上将低阶模型与最优控制问题相结合提出了基于低阶模型的二维对流扩散边界控制问题. 首先采用有限差分法计算出由瞬时对流扩散方程解集构成的瞬像(snapshots), 再利用奇异值分解[8]和POD分解方法获得对流扩散瞬像的最优特征正交基, 再与伽辽金投影方法结合将高阶的状态空间模型转化为精度较高的低阶模型, 并结合线性二次调节器的最优控制方法, 得出基于无约束的线性二次调节器的最优反馈控制的输入/输出. 以二维对流扩散边界控制问题为例, 结果表明在保证较高精度的优化结果的同时可大幅度提高求解速度.
5 结 论
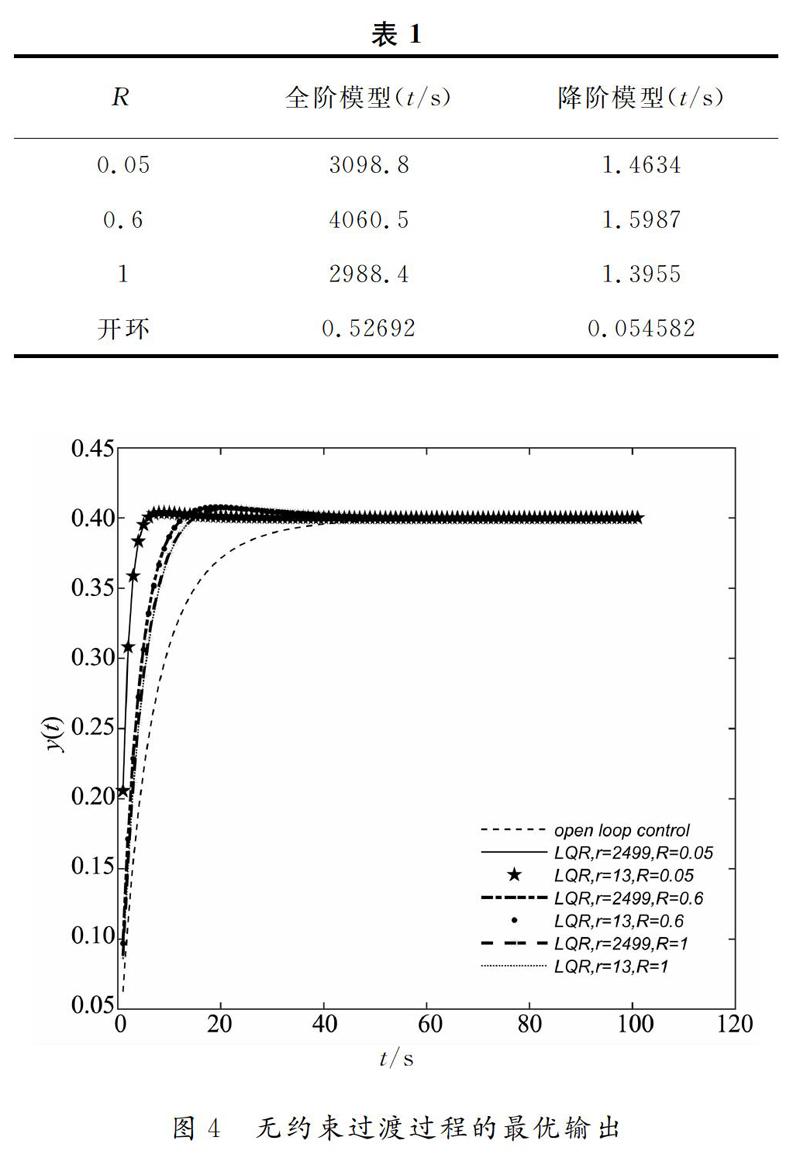
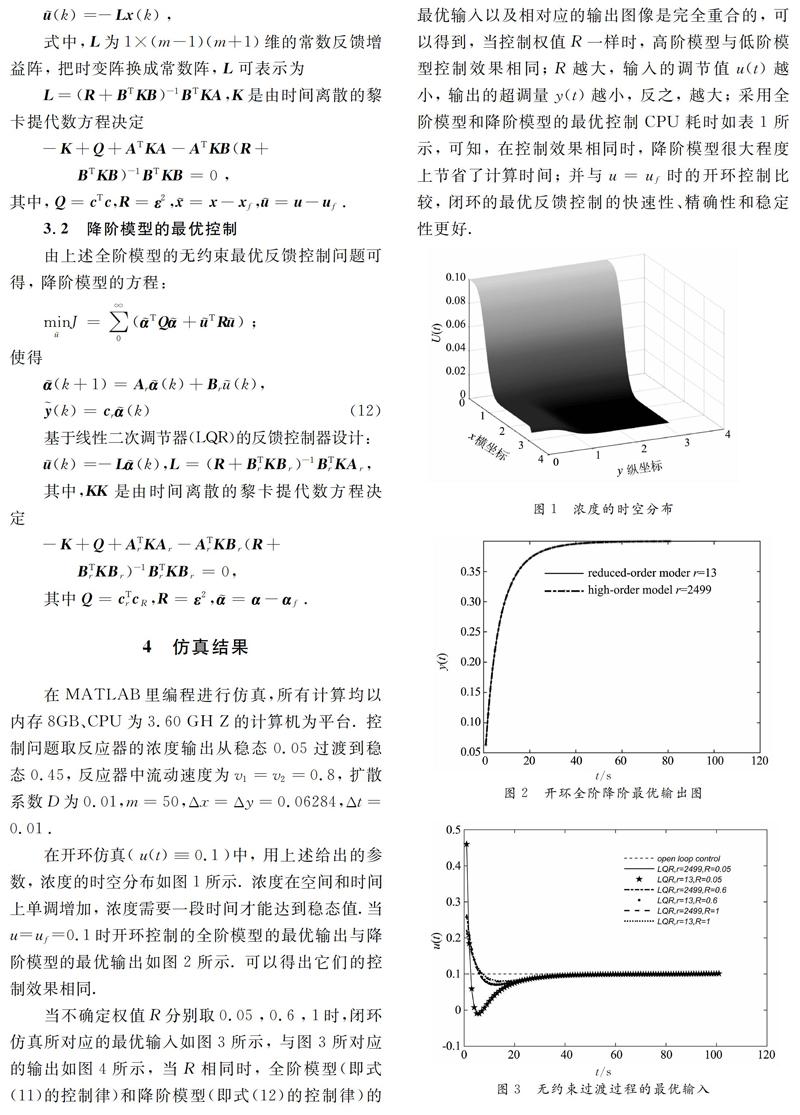
本文应用POD方法提出了基于低阶模型的对流扩散最优控制问题, 基于该方法, 从两个层次上提高了计算和优化的效率, 从以上仿真可以看出, 全阶模型在每个时间步上需要求解2499个方程, 但降阶模型在每个时间步上只需要求解13个方程, 而且, 当空间步长变小时, 全阶模型在每个时间步上需要解的方程的个数将会增多, 而降阶模型在每
个时间步上还只是求解13个方程, 不但解决了对流扩散离散系统计算量大的问题, 并节省了计算机内存和计算时间. 在最优反馈控制中, 基于高阶模型的状态空间模型设计, 所需要的计算内存和时间都比较多, 相对于低阶模型所需要的计算时间就要少得多, 且基于高、低阶模型具有相同的控制效果. 这些都体现了降阶模型的有效性和高效性.
参考文献
[1] XIONG C, LI Y. Error analysis for optimal control problem governed by convection diffusion equations: DG method[J]. Computational and Applied Mathematics, 2011, 235(10):3163-3177.
[2] 胡健偉, 汤怀民. 微分方程数值方法[M]. 北京:科学出版社, 2007.
[3] MUNYAKAZI J B. A uniformly convergent non-standard finite difference scheme for a system of con-vection diffusion equations[J]. Computational & Applied Mathematics, 2015, 34(3):1153-1165.
[4] EGGER H, SCHBERL J. A hybrid mixed discontinuous Galerkin finite-element method for convection-diffusion problems[J]. Ima Journal of Numerical Analysis, 2018, 30(4):1206-1234.
[5] 罗振东, 王瑞文, 陈静, 等. 非定常的Navier Stokes方程基于特征正交分解的差分格式[J]. 中国科学:, 2007, 37(6):709-718.
[6] LENTH R V. Least-squares means: the R package lsmeans[J]. Journal of Statistical Software, 2016,69 (1):1-33.
[7] LI M, CHRISTOFIDES P D. Optimal control of diffusion convection-reaction processes using reduced order models. Computers & Chemical Engineering, 2008 , 32 (9 ):2123-2135.
[8] DERKSEN H. On the Nuclear norm and the singular value decomposition of tensors[J]. Foundations of Computational Mathematics, 2016, 16(3):779-811.

