基于污染混沌动力系统的序列加密算法

许 佳 佳

(四川外国语大学成都学院 经济管理系，成都 611844)

0 引 言

信息安全不仅关乎国家利益还关乎老百姓的切身利益，研究信息安全问题有着重大的学术与实际意义[1-7]。如何把信息进行伪装与隐藏已经成为人们关心的话题，也是信息安全部门研究的新方向，更是密码学学者研究的重点。

最近几年在序列密码加密方面，文献[8]提出了以混沌理论作为基础的应用字符串的加密算法，该加密算法的运算量小，灵活性强；王林林在文献[9]中提出了一种加密算法，这种算法能够在确保迅速加密的基础上，使得混沌系统产生的混沌序列结果具有较强的随机性，加密系统在防攻击性、安全性等方面都优于那些基于联合混沌和基于三维混沌密码的加密系统；柳扬等[10]研究了基于可变参数的混沌动力系统的序列密码，研究了动力系统经平移变换之后新的动力系统与原动力系统具有相同的不变测度与均值，并且在新的动力系统基础上采用序列密码设计了加密与解密的算法。2014年李占梅[11]首次引入不变的污染系数，构造了基于一维Logistic映射和分段线性映射的污染混沌动力系统，并提出相应的加密算法。

本文基于对文献[11]的研究，引入了一个不断变化的污染系数，构造了污染系统，进而介绍序列加密算法。第1节介绍了污染混沌动力系统的定义与例子，第2节基于污染混沌动力系统，介绍了本文的加密解密算法；第3节针对本文的加密算法进行计算机仿真；第4节对本文的加密算法进行安全性分析及相关检验，第5节是本文的结论。

1 污染混沌动力系统的加密算法

1.1 污染混沌动力系统的定义与例子

定义1 设f1和f2是两个动力系统，称f=αf1+(1-α)f2为污染动力系统。其中，0<α<1称为污染系数[11]。选取抛物线映射[12]：

f1(n+1)=X(n+1)=μxn(1-xn)，μ∈(0，4)，xn∈[0，1]

(1)

当μ∈(3.6，4)时，映射出现分岔，是混沌映射。x随μ的变化如图1所示。

分段非线性映射[13]:

f2(n+1)=x(n+1)=

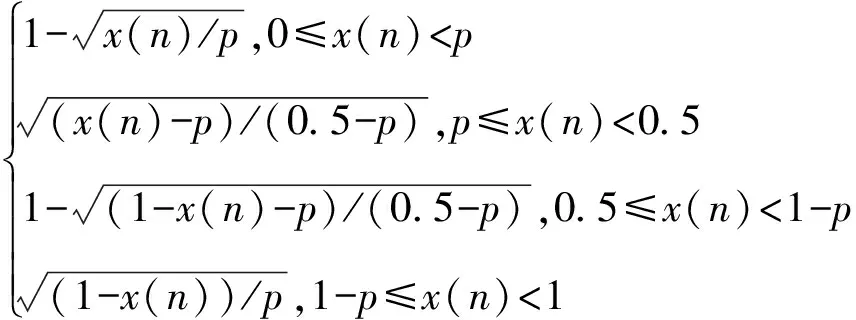
(2)

其中，x∈[0，1]，p∈(0，0.5)。在p=0.25时，分段非线性映射的图像如图2所示。

图2 分段非线性映射图

由抛物线映射式(1)与分段非线性映射式(2)形成的污染混沌动力系统为

f(n)=αf1(n)+(1-α)f2(n)

(3)

当α=0.099，μ=0.2，p=0.25时，并且α=0.008 9，μ=3.8，p=0.15时的污染动力学系统式(3)的图像分别如图3和图4所示。

图3 α=0.099，μ=0.2，p=0.25污染系统

图4 p=0.15，α=0.008 9，μ=3.8污染系统

由图3和图4可知，当p，α，μ取不同值时，污染系统的输出值相差很大。

证明在各参数取值范围内取

另一方面当0.5≤x<1时

又因为

求导可知，q1(x)在定义域内单调递增，且

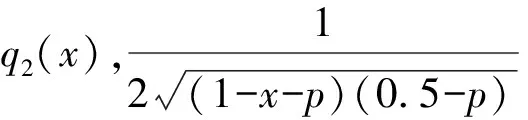
当0.5≤x<1-p时，

综上可知：

|f′|>1

本文在各参数取值范围内选取

初值选取

x(1)=0.195，α(1)=0.001，p(1)=0.22，

μ(1)=3.66，n=1 500

则该污染混沌动力系统输出值x(n)的值如图5所示，显然输出结果在[0，1]上服从均匀分布。

图5 污染混沌动力系统输出值的分布

1.2 加密解密算法

加密思想：在传输密文过程中，如果明文信息有变化密文也会变化，密钥的微小变化也会引起密文的改变，本文的加密算法考虑了以上两个影响因素。首先把原始明文信息转化为相应的二进制序列，由初值出发通过污染系统的迭代得到混沌结果序列，把混沌序列处理后得到密钥序列，最后把明文序列与密钥序列进行特殊运算以得到效果更好的密文。加密过程如图6所示：

图6 加密过程框图

具体加密算法如下：

步骤1将明文字符串转化为ASCII码，再将ASCII码值由十进制转化为十六位二进制，得到二进制的明文序列D={d1d2d3…dL}，L∈N+；其中di只取0或1。

步骤3由Tj(x(i))=[10jx(i)]mod 2计算得到密钥序列{ki}。

步骤4加密。第一轮加密后得到第一轮密文si，明文与密钥序列的相邻bit影响第一轮密文，第二轮加密则是把第一轮密文与密钥逆序列异或，得到最终密文mi序列，这样保证了密文的不可攻击性，进一步加强了密钥对密文的影响。

第一轮加密：

第二轮加密：

最后得到密文序列M={m1，m2，m3，…，mL}。

解密图如图7所示，解密时，第一轮解密得到第一轮密文si，第二轮解密时与密钥ki，ki-1异或得到两个相邻明文di，di-1的异或值yi，再用d1与yi+1层层异或逐步得到d2，d3，…。

图7 解密过程框图

具体解密过程：

步骤1取定系统值。

给定污染混沌动力系统中的初始值，则迭代系统中其他参数值为

并代入污染混沌系统中进行迭代，得到混沌序列{x(i)}，i=1，2，3，…，L。

步骤2得到密钥。

由Tj(x(i))=[10jx(i)]mod 2计算得到密钥序列ki=Tj(x(i))，i=1，2，3，…，L。

步骤3解密。

第一轮解密：

第二轮解密：

步骤4得到明文序列。

D={d1d2…dL}

步骤5转化为明文。

将明文二进制序列的ASCII码值转换为明文。

1.3 算法仿真

为了更清楚地说明加密算法的加密过程，对加密算法进行性能分析，下面给出一个例子，对一段文字用Matlab进行加密。

明文：个人信息的安全性

首先将明文文字转化成ASCII码值，然后转化为十六位二进制序列，得到明文序列：010011100010101001001110101110100100111111100001011000000 110111101110110100001000101101110001001010100 01011010000110000000100111。

(1)在原初值条件下的密文为“〗?z宻J? ガ”。

(2)当x(1)=0.195 000 1密文为“?┉Ut'.犧y鵎?”。

(3)将j=7改为j=9密文为“B鲇Y(进;賗株?S”。

(4)将α(1)=0.01改为α(1)=0.000 1，密文为“8V?緧ェ蕾l笒”。

(5)将p(1)=0.22改为p(1)=0.220 001，密文为“踻<_x0019_憖饪??f袲e”。

(6)将μ(1)=3.66改为μ(1)=3.660 001密文为“? /!_x0016_??O琲贊E”。

(7)当x(1)=0.195 000 01，j=8时，其他值不变“F3-?"琐,Y庣婄”。

以上(1)～(7)的结果用0，1二进制序列表示后，如图8所示。分析图形结果，初始值的极微小的变化会使得密文产生巨大变化。

图8 不同条件下明文与密文二进制序列图

当输入正确的解密密钥时，可以得到正确的原始明文信息。如把步骤(1)中x(1)=0.195中输入污染混沌动力系统，得到的密钥流与密文流进行多次异或就得到正确的明文信息，而把密钥当作x(1)=0.195+10-16时，得到的明文为“>楑桳D?設8P谩”。由此可见，输入错误密钥不能得到正确的明文信息。

2 安全性分析及相关检验

2.1 均匀分布特性

判断污染混沌动力系统加密效果的好坏，要看加密后密文流二进制序列中0与1的个数是否接近，越接近加密效果越好。污染系统式(3)中，在指定范围内取定参数值，代入后得到混沌序列，再经过计算得到密钥流。当n取值越来越大时，密钥流中0与1的个数几乎相等，这说明密文流是均匀分布的，该污染系统有良好的随机性质，可以有效抵抗统计分析。

图9 0在密文序列中所占的比例

由图9可知，当n增大时，0在密文流中所占的比例逐渐接近0.5，说明密文流中0与1的个数几乎相等，可见密文是均匀分布的，可以有效抵抗统计分析。

2.2 相关性分析

在参数取值范围内选取密钥值，通过污染系统运算后产生密钥值，对明文进行加密，通过明文与密文的相关度检验加密效果。

定义明文与密文的相关度[12]：

设{d1d2d3…dn}为明文信息的二进制序列，{m1m2m3…mn}为密文流的二进制序列，α，μ，p均为式(3)中的参数。

R(x(1)，α(1)，p(1)，μ，j，n)=

例1 明文为混沌密码学原理及其应用，污染系统中各参数值为初值：x(1)=0.195,a(1)=0.000 1,p(1)=0.22,μ(1)=3.66，以上明文的二进制序列长度为176，则n最大取到176，迭代系统中其他参数满足：

明文二进制、密文二进制以及明文与密文的相关度值随n的变化情况如图10所示，由图10可知，随着n的不断增大，明文与密文的相关度值逐渐趋近0。

图10 明文与密文及其相关度值

通过以上例子，可以得到结果：明文与经过该污染系统加密后的密文相关度很低，并且随着n值的不断增大，相关度值逐渐趋近于0，说明加密后的明文与原始明文几乎不相关。

2.3 灵敏度检验

灵敏度[13]的定义：

设{d1d2d3…dn}为明文信息的二进制序列，{m1m2m3…mn}为密文流的二进制序列。

灵敏度δ(di，mi，x(1)，α(1)，μ(1)，p(1)，j，n)=

用密钥{x1，α(1)，μ(1)，p(1)，j}={0.195，0.001，3.66，0.22，7}

对长度为10 000的0序列加密，得到的明文与密文灵敏度如图11所示。

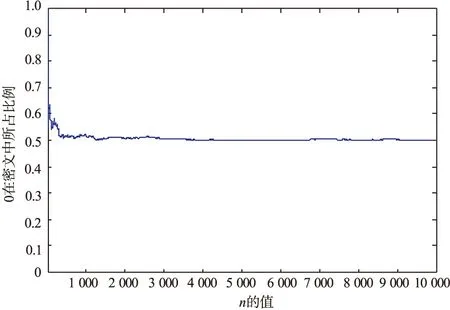
图11 密文与明文的灵敏度

当取不同密钥时，分别选取x(1)={0.195，0.195 02，0.195 04，0.195 06，0.195 08}对10 000个0序列加密后，明文与密文的灵敏度如图12所示。

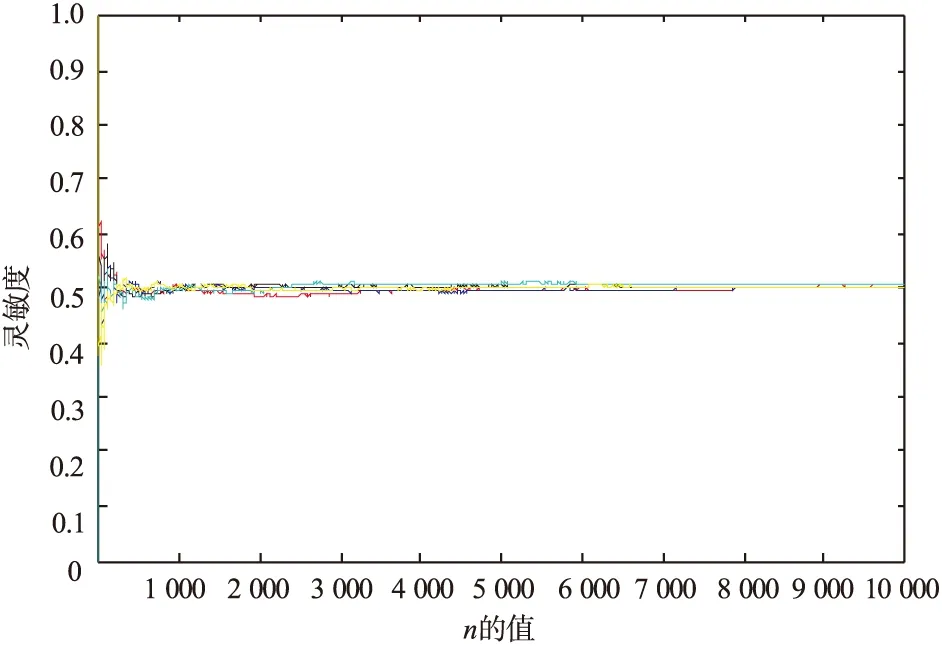
图12 不同初值下密文与明文的灵敏度分析图

取p(1)={0.22，0.220 002，0.220 004，0.220 006，0.220 008},对10 000个0序列加密后，明文与密文的灵敏度如图13所示。

图13 不同p值下密文与明文灵敏度

当j={5，6，7，8，9}时，密文与明文的敏感度如图14所示。密文与明文之间随着信息量以及各个密钥的变化灵敏度在变化，几乎趋近于0.5。说明加密时明文信息会以0.5的概率改变。

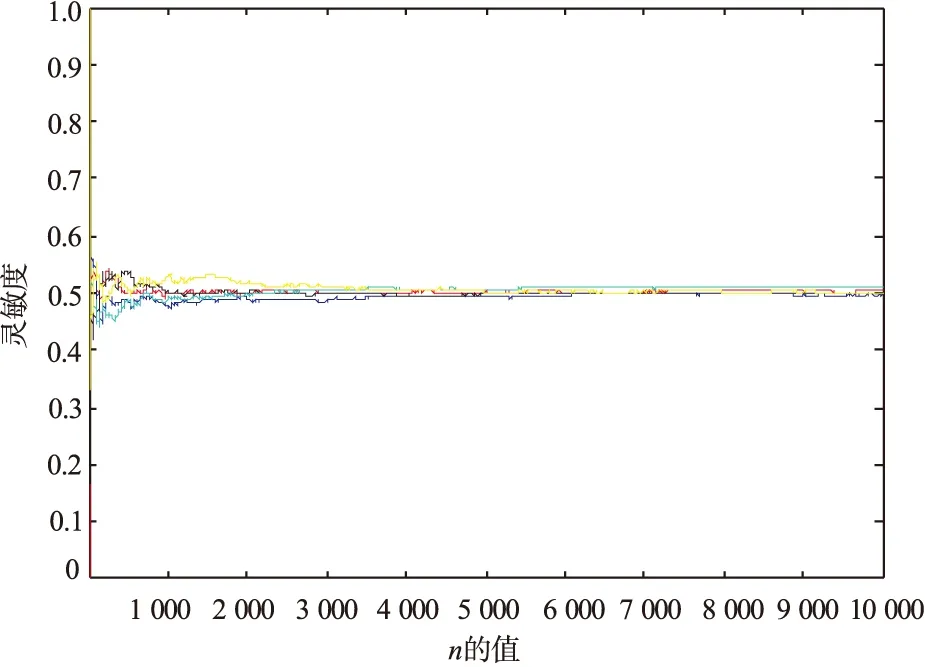
图14 不同j值密文与明文的敏感度

2.4 平衡度检验

设{m1m2m3…mn}为加密后的密文二进制序列，定义平衡度：

n1，n0分别是序列中1，0的个数。平衡度越小，0与1的个数越接近，获得的密文随机性越好。

取密钥x(1)=0.195,a(1)=0.001,p(1)=0.22,μ(1)=3.66。长度为10 000的0序列加密，得到密文的平衡度分析图如图15所示。

图15 密文的平衡度分析图

由图15可知，明文全是0时，密文的平衡度接近于0，说明密文中0，1个数大体相等，对于更一般的明文，密文更有随机性。

2.5 密文序列的自相关性检验

定义二值序列的自相关系数为

其中，m为步长，n为比较的密文长度bit数，自相关系数的值与步长m及n有关，当m一定时，自相关系数与n有关，当n变化时，如果自相关系数变化很小，说明密文序列随机性越好。当m=1，m=2，m=3时，做比较的密文长度为10 000时，用密钥x(1)=0.195，α(1)=0.001，p(1)=0.22，μ(1)=3.66得到的密文自相关系数与n的图像如图16所示。可以看出，当步长分别取1，2，3时，密文序列的自相关系数变化很小，说明密文的随机性很好。

图16 密文的自相关系数图

2.6 密钥空间分析

对于选取的密钥为x(1)，α(1)，p(1)，μ(1)及离散化算子j，若计算机精度为10-5估算本算法的密钥空间，结果密钥空间为5×1025，实际上计算机的精度远大于10-5，则密钥空间远大于5×1025，由此可知该污染混沌动力系统有足够大的密钥空间可以抵抗穷举攻击。

3 结 论

文章介绍的密码算法是基于污染混沌动力系统的加密算法，使得简单的映射能产生足够安全的密文，真正做到了明文任一比特的改变都能引起密文的巨大改变。本文介绍了由抛物线映射和分段非线性映射构造的污染混沌映射，用计算机模拟实例来验证加密的结果，并且进行了多项加密性能分析，如密文是否均匀分布、平衡度以及密文的自相关性等，分析后表明该加密算法加密效果良好，密文及算法都可以有效抵抗攻击。