预应力钢筋回缩引起的预应力损失简化计算研究

龚良勇， 王俊召

(重庆交通大学 土木工程学院， 重庆市 400074)

自20世纪50～60年代起中国混凝土桥梁建设逐渐起步，各种大型简支梁、悬臂梁等预应力混凝土桥梁一一落成，为中国大型后张法预应力混凝土桥梁的修建积累了丰富的经验。进入21世纪之后，预应力混凝土桥梁在中国公路桥梁建设中得到了广泛的应用。预应力混凝土梁分为先张法预应力梁和后张法预应力梁，目前世界上使用最为广泛的是后张法预应力混凝土梁。但是在预应力筋拉伸完毕锚固时由于锚具压缩，锚具与梁体之间存在的接缝被压密等原因会造成预应力钢筋的回缩，使得实际加载的有效预应力偏小。造成了预应力桥梁结构的承载能力打折扣，也使得桥梁的耐久性受到不利影响。目前一些研究表明，预应力混凝土桥梁建成投入使用后，其预应力损失可达到30%左右，局部位置预应力损失可达45%以上。因此有必要对预应力回缩引起的预应力损失情况进行研究。以便确定预应力损失量，为实际加载的张拉量提供依据。

1 国内外研究现状

目前，预应力损失测量与计算方法有很多种，大多数都是基于试验的基础结合理论分析与建模进行研究。有研究者将预制预应力钢筋混凝土梁的预应力损失分析与试验中观察到的预应力损失进行比较，以模拟评估分析方法计算预制预应力钢筋混凝土梁的预应力损失。预应力损失的测量一般借由裂缝、挠度、动力性能等具体指标的检测来推断预应力梁中的预应力筋工作状况，这些手段都能够间接地推测梁体的整体工作状况以及判断预应力损失量，但是对预应力筋的实际状态(预应力损失、有效预应力等)做出有效的判断方法或是繁琐，或是难以把控准确度。因此对预应力损失的测量计算方法有必要进行研究。

2 预应力钢束回缩引起预应力损失研究

该文将采用一种基于测量预应力筋回缩量的数值计算方法来检测预应力的损失。

预应力筋在张拉完成后由于种种原因会产生回缩，具体原因如下：

(1) 锚具被预应力压缩产生的变形。

(2) 锚板和垫板间原有空隙被压密产生的变形。

(3) 锥形锚具被千斤顶挤压时使预应力筋回缩。

(4) 夹片式锚具在锚固时由于夹片被挤进夹槽也会产生预应力筋回缩。

研究过程为：首先利用精密的仪器测量出预应力筋的回缩变形量，并根据公式计算出所对应的预应力损失值。然后将根据设计资料建立梁的有限元模型，并利用有限元模型计算对应的预应力损失，验证公式计算结果是否可靠。具体研究思路如图1所示。

图1 研究思路框图

3 预应力钢束回缩应力损失理论公式计算法

对于后张法预应力混凝土结构，当预应力筋为曲线和折线布置时，钢筋与孔道壁的摩擦较大，此项预应力损失就集中发生在靠近张拉部位的预应力筋内，需要考虑反向摩擦的影响。用平均摩擦系数代替实际摩擦系数，忽略摩擦系数沿预应力筋长度方向的不同。同时假设预应力钢筋回缩时反摩阻作用机理与张拉时摩阻作用机理相同，就可以计算出预应力钢束回缩的影响长度和张拉端的预应力损失，进而求得距张拉端不同距离处考虑反摩擦后的预应力损失。

综上所述，在建立理论公式对预应力筋进行应力值计算时，作出如下假定：

(1) 用平均摩擦系数代替实际摩擦系数，忽略摩擦系数沿预应力筋长度方向的不同。

(2) 预应力钢束回缩时反摩擦阻力与张拉时正摩擦阻力大小相同，方向相反。

当不考虑波纹管孔道壁对预应力筋摩擦力的影响时，据JTG/T F50-2011《公路桥涵施工技术规范》，由预应力筋回缩引起的预应力筋损失量σ1的计算公式如下：

(1)

式中：Δl为张拉端锚具变形、钢筋回缩和接缝压缩值；l为预应力钢筋的总长度；Ep为预应力钢筋的杨氏弹性模量。

但是当预应力孔道是抛物线或者圆曲线时预应力钢筋和预应力孔道间就会产生反摩擦力。由于反摩擦力的作用，由预应力钢筋引起的预应力损失值会随着位置的不同逐渐变化。

研究表明，反摩擦力对预应力钢筋回缩引起的预应力损失的影响是有一定长度的，即影响长度ly。在影响长度内，由于靠近张拉端的预应力钢筋回缩最大，因此预应力损失也最大，随着距离张拉端越来越远，预应力的损失也越来越小，当距离超过影响长度时预应力钢筋的回缩量变为零，预应力的损失量也变为零。

如图2所示，曲线ANC是预应力钢筋回缩前的预应力随着钢筋远离张拉端的变化曲线，A端是张拉端，当x=0时此处的预应力值是张拉控制应力σ0。从图2可以看出：当距离A点越来越远时预应力值是越来越小的，其原因是张拉预应力钢筋时会有摩擦力的作用，这个摩擦力被称为正摩擦力。曲线A′NC是预应力钢筋回缩后的预应力随着钢筋远离张拉端的变化曲线，N点到D点的距离是影响长度ly。由于摩擦系数相同，可以近似认为正反摩擦力在大小上是相等的，所以在影响长度范围内，曲线AN与曲线A′N是关于DN对称的。曲线AN与曲线A′N之间的距离即是预应力钢筋回缩产生的预应力损失值。从图2可以看出：随着距离张拉端越来越远，预应力损失越来越小，到N点后预应力不再损失。

图2 预应力损失示意图

摩擦力对预应力大小的影响值σ2(x)如图2所示，可用式(2)计算得到。

σ2(x)=σ0[1-e-(μθ+kx)]

(2)

由于-(μθ+kx)非常小，而根据公式ex≈1+x可得：

σ2(x)≈σ0{1-[1-(μθ+kx)]}=σ0(μθ+kx)

(3)

因此可以知道曲线AN可近似地视为一条直线，如图3所示。

图3 预应力近似值示意图

通过图2和式(3)可以推得：

(4)

在影响长度内的预应力钢筋的总回缩量∑Δl的计算公式为：

(5)

由式(5)可以推导得出：

(6)

将式(4)代入式(6)可以推出：

(7)

最后将式(7)回代入式(4)可以得到最终的预应力损失公式：

(8)

式中：σ0为预应力钢筋的张拉控制应力；ly为摩擦力对预应力损失的影响长度；μ为预应力钢筋和孔道壁间的摩擦系数；θ为张拉端到需计算处的孔道弯曲角度；k为孔道壁偏差摩擦影响系数(1/m)；x为张拉端到需计算截面的孔道长度；θy为影响长度内预应力钢筋的弯曲角度(rad)；rd为张拉端到需计算处的孔道的等效曲率半径。

4 利用假定回缩量计算损失量

4.1 各参数取值与假定

预应力钢筋的回缩值应当采取实际测量得出的数据，但是当无实测数据时，可按表1取用。

表1 预应力钢筋回缩的一般值

表1中实测预应力钢筋有效长度为l=10.5 m，锚具变形及锚塞顶压引起的预应力钢筋回缩∑Δl=6 mm，在此基础上进行预应力损失的计算。

由于采用的是金属波纹管，故k=0.0015(1/m)，预应力钢筋是光面钢绞线，所以μ=0.23。另外根据梁体设计图纸，得到rd=5 m，Ep=2.1×1011Pa。

对于张拉控制应力σ0的限值参照表2。

表2 张拉控制应力限值

表2中：fpk为预应力钢筋的抗拉强度标准值，fpk=1.8×109Pa，所以可取σ0=0.75fpk=1.35×109Pa。

以上各参数值汇总如表3所示。

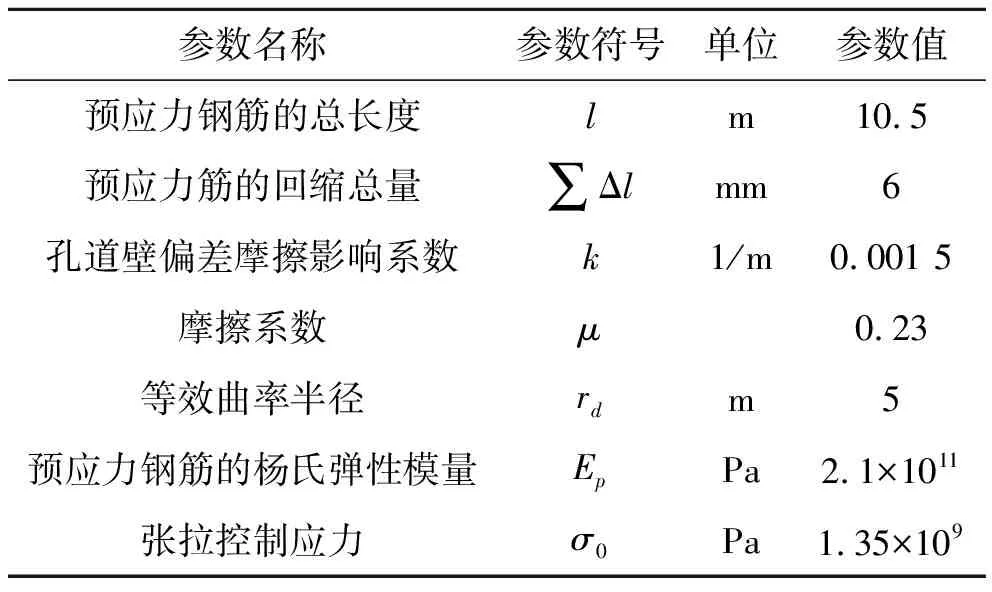
表3 参数取值汇总

4.2 影响长度的计算

将表3中的参数值代入式(7)，计算得：

4.3 预应力损失的计算

将表3中的参数值代入式(8)，得：

根据公式计算到张拉端每隔0.2 m的位置上预应力筋中的预应力值，结果如表4所示。

5 有限元模拟

5.1 模型建立

表4 理论公式计算预应力值随距离的变化情况

在模型中设置钢筋和混凝土为灌浆之前的上部界面全接触，钢筋弹性模量为2.1×1011Pa，泊松比为0.3，密度为7.8×103kg/m3；混凝土弹性模量为3.25×1010Pa，泊松比为0.2，密度为2.4×103kg/m3。

加载分两步，首先在一端加载σ0=1.35×109Pa的均布压强，待其稳定后，将其换成σ0-σ1max=7.815×108Pa的均布压强。如此，只要端部的回缩量以及预应力筋内部的应力值和理论公式法计算所得应力值接近，则可以认为两种方法所得结果较为一致。

5.2 结果输出

经过有限元仿真模拟，得到了在预应力变化前后预应力钢筋中的应力分布数据，该文从张拉端开始每隔0.2 m采集一个数据，如表5所示。

将表5数据绘制成图4，结合表4，比较理论公式法与有限元方法计算结果的差别。

5.3 结果对比分析

由理论公式计算结果(表4)可知，最大预应力损失在张拉端，损失值为5.685×108Pa，影响长度为4.43 m，超过影响长度之后预应力筋的预应力稳定值为10.675×108Pa。另外可以看出由于文中公式的假定条件，预应力损失随影响位置的变化成线性变化。

由有限元模拟结果(表5)可知：最大预应力损失在张拉端，损失值为5.685×108Pa，影响长度为4.37 m，超过4.37 m后的预应力值为10.701×108Pa。另外可以看出：有限元模拟预应力损失随影响位置的变化呈现一定弧度的曲线变化。

表5 有限元模型计算预应力值随距离的变化情况

图4 理论公式法与有限元模型法结果对比图

从图4可以看出，有限元模拟法中得到的张拉端预应力值与公式法得到的张拉端预应力值大小一致。有限元模拟得到的影响长度外的预应力值为10.701×108Pa，这与公式计算得到的结果(10.675×108Pa)基本相同，表明用文中给出的公式法可以准确计算出影响长度以外的预应力实际值。从而可得出结论：有限元模拟法与公式计算法计算得到的数据吻合。

有限元模拟得到的影响长度为4.37 m，这比公式计算得到的值4.43 m要小一些。考虑产生的原因，主要是因为模拟过程中没有进行假设所以更接近实际情况。公式计算中假设应力损失按线性递减，从图4可以看出有限元模型中的应力损失一开始的速率比较快，后来慢慢递减，故总体的递减趋势要高于公式计算结果，这是其影响长度稍小的主要原因。

为了更加直观地观察公式计算法和有限元模型法计算得到的预应力损失的差别情况，绘制如图5所示的模型法和公式计算的预应力损失差值随张拉端距离的变化情况。

从图5可以看出:两种方法计算的预应力损失差值先增大后减小，其中差值最大的位置距离张拉端2.2 m，此处的预应力差值为1.513×108Pa，也就是说，用公式法计算得到的预应力损失值在距张拉端2.2 m处最不准确，损失误差值与控制预拉应力的比值为1.513×108Pa÷1.35×109Pa≈11.2%。

图5 理论公式计算与有限元模型计算预应力损失差值随距离变化图

6 结论

利用理论公式的数值计算法和有限元模拟法两种方法，对同一预应力钢筋混凝土梁进行了预应力钢束回缩产生的预应力损失研究，通过公式计算法和有限元仿真模拟的结果对比分析，得出以下结论：

(1) 有限元模拟方法与理论公式计算法得到的预应力损失最大值均出现在张拉端，且损失量大小一致，均为5.685×108Pa。

(2) 有限元模拟方法与理论公式计算方法得到的预应力损失影响长度大小基本一致，分别为4.37和4.43 m。

(3) 有限元模拟方法和理论公式计算方法得出超过预应力损失影响长度后，预应力筋预应力值趋于稳定，稳定值分别为10.701×108Pa和10.675×108Pa，两者相差较小，结果可信。

(4) 有限元模拟方法与理论公式计算方法得到的预应力损失值进行相减，差值变化规律为，由张拉端开始到稳定点逐渐增大后变为逐渐减小，最大差值大致出现在预应力损失影响长度一半处，最大预应力损失差值与控制预拉应力之比为11.2%，即此处理论公式计算方法得到的预应力损失量较为不准确。

综上可知，该文提供的理论公式计算法可以作为一种较为简便的预应力损失量计算方法，有利于在工程实践中应用并再次检验，比有限元模拟计算方法具有简便快捷的优势，能满足实际工程中计算预应力张拉控制值的需求。