混合梁斜拉桥钢-混结合段受力性能的有限元分析

金龙， 杨永伟， 邓露， 王子文， 刘秉辉(.四平市城市发展投资控股有限公司， 吉林 四平 36000； .中铁九局集团第二工程有限公司；

3.湖南大学 工程结构损伤诊断湖南省重点实验室； 4.长吉城际铁路有限责任公司)

桥梁是交通工程中的关键性枢纽，在交通运输和发展中起非常重要的作用。近年来，组合结构已经被越来越多地应用于桥梁工程，其中混合梁斜拉桥因其良好的结构性能、技术优势和经济效益得到迅速发展，如九江长江公路大桥、二七长江大桥等均采用混合梁斜拉桥。

钢-混结合段是混合梁斜拉桥的关键结构，其受力性能直接影响全桥的安全性及可靠性。钢-混结合段主要由钢、混凝土构件和抗剪连接件(剪力钉和PBL剪力键)组成，构造细节十分复杂。同时钢-混结合段也是主梁结构刚度突变点，传力机理复杂，容易引起局部应力集中，甚至导致结构失效。而目前尚无统一的理论用于计算和评估其承载能力和局部受力性能，因此对钢-混结合段的研究通常以模型试验为主。但模型试验耗资过大，试验周期较长，难以保证测量精度，而且各个工程中钢-混结合段的构造细节差异很大，导致研究成果对工程实践的参考价值有限。因此有必要利用有限元软件对钢-混结合段进行精确的数值模拟和计算分析。其中，抗剪连接件作为钢-混结合段的关键构件，主要传递钢梁和混凝土梁之间的内力。研究表明：混合梁斜拉桥的钢-混结合段内靠近混凝土梁的剪力钉群在荷载作用下刚度有所下降，而钢-混组合梁桥中群钉受力极不均匀，部分剪力钉受力远超平均水平。此外，赵晨和朱伟庆等的研究指出，现有的PBL剪力键的受剪承载力计算公式因受制于试验条件而导致计算结果差异较大。因此，钢-混结合段内抗剪连接件的受力性能值得关注。该文以某混合梁斜拉桥为例，建立其钢-混结合段的精细化有限元模型，研究钢-混结合段内各个构件的应力分布和受力情况。

1 工程背景

采用某单索面独塔混合梁斜拉桥为工程背景，其结构采用塔-梁-墩全固结体系。主桥全长259 m，桥面宽36 m，跨径布置为(90+169) m，采用钢梁+混凝土梁的结构形式。设计中心线处梁高3.4 m，梁顶设1.5%的双向坡，梁底水平。钢箱梁采用单箱九室截面，混凝土梁为等截面预应力箱梁，采用纵、横向预应力体系，墩位处及拉索区均设置横梁。钢梁与混凝土梁通过钢-混结合段连接，钢混分界线位于主跨侧距桥塔中心11.5 m 处，在该处设置40 mm厚的承压板。钢-混结合段长2.25 m，结合面钢箱梁侧加强段长3.4 m，设置了T形和U形两种加劲肋进行增强，结合面混凝土梁侧过渡段长5 m，其顶板、底板和腹板板厚均为渐变形式。

图1 钢-混结合段纵断面图(单位：mm)

2 有限元模型的建立

2.1 模型概况

采用空间混合有限元方法建立钢-混结合段的Ansys三维节段模型，分析钢-混结合段在最不利工况下的受力状态。基于圣维南原理，选取钢混分界线两侧14.3 m范围的梁段建模，其结构主要包括4.85 m长的混凝土箱梁、2.25 m长的钢-混结合段和7.2 m长的钢箱梁。钢-混结合段有限元几何模型如图2所示。由于建模选取的节段为轴对称结构，为提高计算效率，有限元模型取横桥向半幅箱梁段，并在中心截面处采用对称的位移约束条件。混凝土箱梁采用C50混凝土，弹性模量E=3.45×104MPa，泊松比υ=0.167；钢箱梁构件主要采用Q345钢材，弹性模量E=2.1×105MPa，泊松比υ=0.3。预应力钢束采用φs15.2钢绞线，公称抗拉强度fpk=1 860 MPa，弹性模量E=1.9×105MPa，预应力张拉控制应力为0.75fpk。

图2 钢-混结合段有限元几何模型

2.2 单元类型

钢构件采用Shell63单元模拟，板厚通过实常数设置；混凝土采用Solid65单元模拟，不考虑混凝土中的普通钢筋和横向预应力，钢构件与混凝土的材料属性均设置为线弹性本构关系；剪力钉采用Combin39单元模拟，Combin39单元的两个节点位置完全重合，分别与混凝土单元和钢板单元进行约束；PBL剪力键采用Beam4单元模拟，与混凝土的接触采用约束方程，与开孔板的接触采用节点耦合；预应力钢绞线采用Link8单元模拟，采用降温法施加预应力，通过约束方程模拟预应力筋和混凝土间的黏结作用；钢板与混凝土间设置接触单元，采用Conta173单元和Targe170单元模拟，忽略接触面间的摩阻力。

2.3 边界条件及荷载施加

有限元模型中，在混凝土箱梁端面处采用固结约束。假定钢梁远端为平截面变形，施加荷载时，在钢箱梁端面处生成刚性面，在刚性面的中性轴处建立质量单元，生成刚性线，并与钢箱梁端面的刚性面连接形成刚性区域，将设计荷载等效地施加在刚性区域的主节点上。设计荷载值取自Midas全桥模型最不利工况下的截面内力，包括轴力107 504 kN、弯矩49 950 kN·m和剪力801 kN。由于扭矩较小，该文计算时忽略其影响。

3 钢-混结合段整体有限元分析

3.1 钢梁计算结果与分析

在设计荷载作用下，分析有限元模型中钢箱梁结构的轴向受力情况。由计算结果可知：钢箱梁结构的轴向正应力范围为-127～78 MPa(负值表示压应力)， 除了几处存在应力集中现象外，绝大部分区域处于受压状态，且压应力基本低于60 MPa。应力集中现象主要发生在钢箱梁底板折角与横隔板交接处、钢箱梁加强段加劲T肋尾端、斜底板和腹板交接处等部位。但由应力集中导致的高应力区域范围都较小，且最大应力仍远低于Q345钢的屈服强度，所以不影响结构的整体性能。

图3为钢箱梁各板件的轴向正应力沿纵桥向的变化情况。

图3 钢箱梁轴向正应力

由图3可知：钢箱梁各板件沿纵桥向的应力变化趋势相似，均表现为加载端应力较大，钢箱梁标准段应力分布均匀，变化平稳。由于钢箱梁加强段主梁截面增大，T形加劲肋对钢箱梁板件应力的扩散作用较为明显，有效地使各板件应力逐渐降低，而钢-混结合段内钢结构与混凝土在抗剪连接件的作用下共同受力，使结合段内各板件的应力进一步降低。

同时，由于结合段负弯矩的影响，底板、斜底板的应力较大，顶板的应力较小。承压板两侧钢梁各板件应力发生突变，说明承压板在应力传递过程中的作用较大。钢-混结合段内钢梁顶底板的应力先均匀平缓下降，在靠近钢梁尾端处急剧降低，说明钢梁应力已有效地传递至混凝土中，而由于钢-混结合段内设置了多个钢格室和较密的抗剪连接件，导致钢-混结合段内腹板的应力水平较低。

3.2 混凝土计算结果与分析

在设计荷载作用下，分析有限元模型中钢-混结合段内混凝土的轴向受力情况，其轴向正应力如图4所示。

图4 混凝土轴向正应力(单位：MPa)

由图4可知：钢-混结合段内混凝土梁的轴向正应力范围为-15～1 MPa(负值表示压应力)，整体应力水平较低，相对于容许值有充足的富余。由于有限元建模时承压板上预应力钢绞线锚固区未设置刚性垫块模型，导致靠近锚固点处的混凝土出现较大的应力集中，部分混凝土承受拉应力，建议在距离承压板0.5 m内的混凝土中设置加固钢筋，防止开裂。此外，钢-混结合段内大部分区域处于受压状态，且压应力基本低于10 MPa。

图5为钢格室内混凝土的轴向正应力沿纵桥向的分布情况。

由图5可以看出：靠近承压板的混凝土应力集中明显且存在拉应力，集中应力在距离承压板0.3 m处开始扩散，到距离承压板0.9 m处混凝土的应力分布已较为均匀，说明钢梁应力先通过承压板和抗剪连接件传递至与其接触的混凝土，再扩散至整个混凝土截面。同时，远离承压板处的混凝土应力逐渐增大，说明结合段内混凝土承担的内力增大，钢-混结合段较好地实现了轴力和弯矩从钢梁向混凝土梁的传递，刚度过渡合理。

4 钢-混结合段抗剪连接件受力分析

4.1 PBL剪力键受力分析

钢-混结合段上、下钢格室内沿梁高方向分别设置了3排PBL剪力键，沿纵桥向共7排。提取各部位PBL剪力键的内力，分别得到钢-混结合段上、下钢格室内PBL剪力键所受剪力的分布情况(图6)。

图5 钢格室内混凝土轴向正应力分布(单位：MPa)

图6 钢-混结合段内各部位PBL剪力键所受剪力

由图6可知：各排PBL剪力键受力大小沿纵桥向的变化趋势相似，剪力大小为10～70 kN，距承压板最远的PBL剪力键所受剪力最大，是其他部位PBL剪力键所受剪力的2～6倍，但远低于文献[15]中由各个公式或试验得出的PBL剪力键的极限抗剪承载力。

由于承压板直接传递的内力较大，因此距承压板最近的PBL剪力键所受剪力较大。而距承压板较远处混凝土集中应力开始扩散，故第2排PBL剪力键所受剪力较第1排变小。但距承压板更远的混凝土承担的内力变大，所以后排PBL剪力键所受剪力逐渐增大。

4.2 剪力钉受力分析

张景峰等分别采用线性剪力钉模型和非线性剪力钉模型对剪力钉的受力情况进行有限元分析，得到的计算结果相近。因此，为了提高计算效率，该文有限元模型中的剪力钉采用简化的线性模型模拟，即将剪力钉的荷载-滑移特性简化为线性。综合文献[16]、[17]中剪力钉抗剪刚度的取值，该文模型中剪力钉的剪切刚度取为300 kN/mm。该桥顶底板沿纵桥向共设置了8排剪力钉，钢格室内设置了5排剪力钉。提取各排剪力钉的内力，得到钢-混结合段各部位剪力钉所受剪力的分布情况，如图7所示。

由图7可知：距承压板最远的剪力钉所受剪力最大，是其他部位剪力钉所受剪力的2～7倍，因此此处剪力钉控制其设计。最大剪力值为23 kN，远低于基于JTG/TD 64-01—2015《公路钢混组合桥梁设计与施工规范》计算得到的剪力钉的抗剪承载力设计值111 kN。各部位剪力钉受力大小沿纵桥向的变化趋势相似，表现为离承压板距离较远的两排剪力钉所受剪力较大，其他部位的剪力钉所受剪力相差不大。

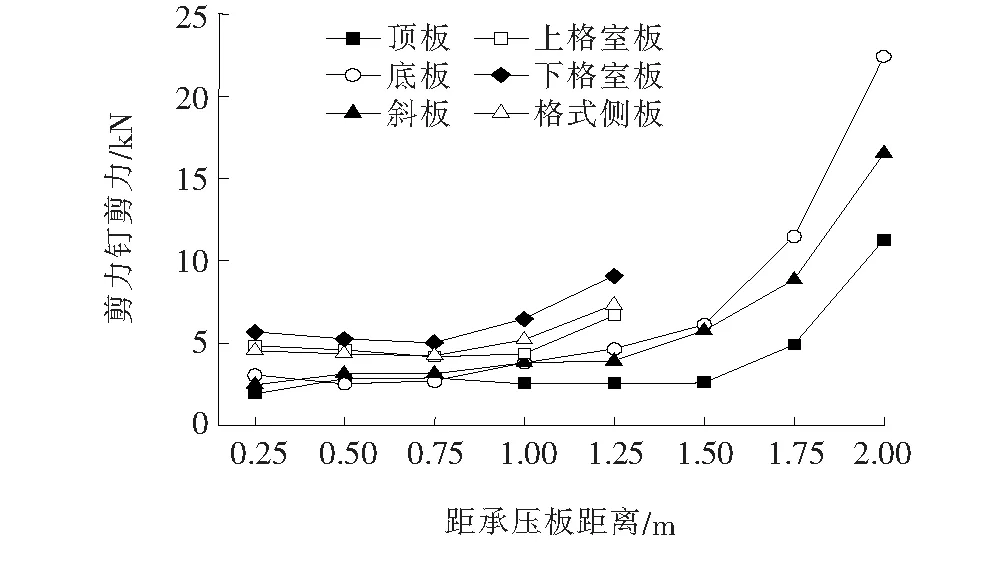
图7 钢-混结合段内各部位剪力钉所受剪力

5 钢-混结合段各部位传力比分析

钢-混结合段传递的内力主要是轴力和弯矩，主要通过承压板承压传力、抗剪连接件承剪传力的方式将钢梁的内力传递至混凝土梁，而弯矩可以等效为作用在上下缘结构的轴向力。分别计算钢-混结合段内各传力构件的总作用力，得到各构件传递轴向力的承载比例见表1。

表1 钢-混结合段各构件承载比例

由表1可知：承压板和PBL剪力键为主要传力构件，剪力钉的传力比例较小，其主要作用是确保钢格室与格室内混凝土紧密结合。

在钢-混结合段内沿纵桥向选取多个截面积分，分别得到混凝土结构的轴力、弯矩传力比例曲线，如图8所示。

由图8可知：承压板直接向混凝土传递约62%的轴力和48%的弯矩。因为该桥只设置了后承压板，所以钢-混结合段内靠近承压板的混凝土承担的轴力比例增长较快。而混凝土横隔梁处截面形式变化较大，导致弯矩的传递比例在该处发生突变。为确保传力效果，建议合理布置靠近承压板和混凝土横隔梁处的抗剪连接件，并保证承压板处混凝土的密实度。

图8 混凝土结构的轴力、弯矩传力比例曲线

6 结论

采用有限元软件Ansys对某混合梁斜拉桥的钢-混结合段进行了数值模拟，分析了其在静力设计荷载作用下的受力性能，得到以下结论：

(1) 在设计荷载作用下，钢-混结合段内各构件的应力均低于标准梁段内的同类构件，且沿纵桥向变化平顺，钢-混结合段能有效传递内力。部分区域存在应力集中现象，但仍满足结构整体受力性能的要求。

(2) 承压板作为主要传力构件，直接传递54.9%的内力，且受力较为复杂。为确保内力在钢梁和混凝土梁之间的平稳传递，需防止承压板处混凝土脱空。建议在设计时合理布置靠近承压板位置的抗剪连接件和钢筋网，并在施工时严格控制该处混凝土的密实度。

(3) 钢-混结合段内剪力钉和PBL剪力键受力不均匀，距承压板最远的剪力钉和PBL剪力键受力最大，但均远低于其极限抗剪承载力。