实测坡度差异分析

龙永清，王 雷，庞国伟，杨勤科

(西北大学 城市与环境学院，陕西 西安 710127)

坡度是地表作为地表形态的基本属性指标,用以描述地表的倾斜程度[1]。坡度同时也是土壤侵蚀[2]、水文模拟[3-4]、滑坡监测[5]、土地利用规划[6-7]、工程设计与施工[8-9]等科学研究与工程领域中最常用的地形因子指标。

有关的研究和应用中,坡度通常通过3种方法来获取,包括基于地形图的量算、基于测量设备的野外测量和基于立体像对摄影测量[10]。随着现代数字地形分析理论与技术的发展,在GIS和数字地形分析中,坡度信息基本都是基于DEM来提取[11-12]。

尽管高分辨率DEM数据提取的坡度、理论曲面坡度均可用于DEM提取的坡度的精度和不确定性分析[13-14],但研究者认为,对于DEM提取坡度的精度评价的基本参照应当是野外实测的坡度[15-16]。因而，在坡地地貌学和数字地形分析中,坡度的野外实地测量一直受到关注。Strahler[17]在野外沿坡度线、在坡度均一的地段布设局地坡地剖面,在其上用坡度尺直接读取坡度;朱震达[18]在黄土丘陵地貌研究中利用了实测方法进行坡度制图;Rapp[19]以简单实用的水平仪和子午仪,沿最大坡降方向,测定十米间距坡度,并绘制坡度图;Hammer[20]等在进行土壤调查与数字高程模型坡度分级对比中也提到了坡度野外实测,以10m间隔,实用倾斜测量仪来进行坡度实测;Yang[21]用电子坡度尺和GPS进行了坡度测量。文中在总结已有坡度实测方法基础上,考虑到现代测量技术(仪器)的进步,对坡度实测方法进行了初步尝试,并基于误差传播理论对实测坡度的精度分布做出了分析,希望对数字地形分析中坡度的精度评价提供技术方法和数据支撑。

1 研究区域与数据获取

1.1 研究区域

烟墩山位于靖边县城西南方向,距县城路线距离约14.5km,按地形地貌分属于黄土高原北部风沙滩区与中部梁峁涧区交界处。研究区位于烟墩山烽火台正南方向一完整小坡面,区域大小约东西宽50m,南北长约110m,最大高程差约为43.5m,上部坡度较缓,中部较陡,下部又逐渐变缓,呈“乙”字型,平均坡度27°。坡面内发育有三条浅沟,左右两侧已经发育为切沟,沟沿线以下侵蚀强烈,沟坡陡峭,按现行要求属于退耕地,坡面上主要以草本类植物,平均高度为10～20cm。研究区位置与基本情况见图1。

图1 研究区域位置Fig.1 Site position

1.2 坡度测量原理与方法

1.2.1 坡度测量原理 坡地地貌学研究认为,地表由一系列坡地单元构成[17, 22-23]。坡地上某点的坡度,是坡面相对于水平地面的倾斜程度,或者是坡地上的坡度线相对于其水平投影的倾斜程度[17, 24-26]。坡度的测量,就是对每个坡地单元(面)或坡地剖面线倾斜程度的测量。从简单几何学原理讲,就是对角α的测量(如图2)。那么,可利用角度测量原理,利用坡度尺、罗盘、经纬仪或全站仪等角度设备,直接测量坡度(直接测量);也可根据坡度的最基本含义(倾斜程度、斜率),利用距离、高程测量原理,精确测量坡度线上一定距离(水平距离或地面斜距离)两端点的高程,然后用三角关系推算出坡度(间接测量)。其中的间接测量方法,其实也是所有坡度计算的基本原理。

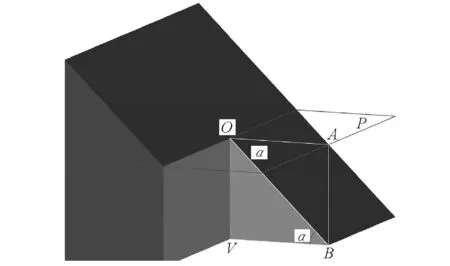
图2 坡度测量原理Fig.2 Principle of field survey slope

1.2.2 坡度测量方法 现在数字地形分析研究中,地理学(地貌学)意义上的地表,是地表组成物质集合体构成连续表面,用能够表现0.5～1m内高程变异的一组高程点来表达[2, 12]。至于小于0.1 m甚至更小范围的变异,通常被认为是土壤表面粗糙度,可用局地高差的标准差等表示[27]。据此,本研究中用1m无变形钢质直杆放置在地面点最大坡降线方向,首先用罗盘在其上读取坡度(直接测量),然后用全站仪在两端点(直杆上及地面点)测量高程(间接测量)。考虑到地面的微起伏,高程测量中,在测杆两端点中间设置2～3个点,观测其高程,用于分析微地形变化对坡度计算的影响。

1.2.3 局地剖面线上的坡度计算 由于地面的各种起伏,测量工作在一定程度上对地面地形的综合表达。本研究在测量计算坡度时拟采用最大坡降法测定计算,测定自然表面两点间下割线坡度——两端点连线的倾斜程度(图3a);上切线坡度——坡度方向剖面线上部的切线的倾斜程度(图3b);拟合线坡度——以坡度方向剖面线的测定的离散点拟合直线的倾斜程度(图3c)。

图3 坡度线示意图Fig.3 Measured Line of Slope

2 坡度计算及精度分析

2.1 三角高程精度分析

三角高程测量是依据直角三角形原理,由测站点(O)测定所观测目标点(A)的高度角β和两间点的倾斜距离S,计算两点间的高差从而获取目标点的高程(式(1)，(2)),由于测区范围小,每测站观测距离小于60m,所以未考虑大气折光与地球曲率影响,i为仪器高,v为目标高。

hOA=S*sin(β)+i-v

(1)

HA=HO+hOA

(2)

由误差传播定律可得:

(3)

ρ=206265″

依据全站仪的测角精度和测距精度可知,mS≤2mm;mβ≤2″,仪器高与目标高量取误差一般在1mm～3mm[28],取平均值2mm作为本次仪器高与目标高中误差,以测区环境可知距离小于60m,高度角小于30°,高差中误差为±3mm,由于本次测量为单测站,测站点高程不变,若不顾及测站点高程误差的影响,所以所有测量点高程中误差均在3mm以内,达到四等水准测量要求[29],完全符合1∶500,1∶1 000,1∶2 000外业数字测图技术规程[30] 。

2.2 实测坡度精度分析

坡度表达了地面的倾斜程度,依据式(4)，(5)可知,如果以角度单位来表达坡度,坡度为地面两点高差与水平距离比值的反正切或高差与倾斜距离比值的反正弦。

α=arctan(h/D)

(4)

α=arcsin(h/S)

(5)

依据式(4)，(5)要求,测定地面两点间的高差及其水平距离或倾斜距离即可计算α。由式(5)可知，坡度的精度直接取决于高差与距离的精度。本次试验中采用固定长度(1m)直杆标定坡向,测量直杆两端点所在位置的高程,通过式(6)计算两点之间的高差,故而其误差可以忽略不计,坡度的精度直接只取决于高差。

hAB=HB-HA

(6)

同一测站测定两点高程,同时保持目标高不变,顾及式(1)，(2)可得

hAB=SOB*sin(βOB)-SOA*sin(βOA)

(7)

根据误差传播定律可得:

(8)

令mSOB=mSOA=ms;mβOB=mβOA=mβ;

取SOA=SOB=Smax;βOA=βOA=βmax，可得

(9)

对式(5)求微分,依据误差传播定律可得

(10)

依据前述可知mS≤2mm;mβ≤2″;Smax≤60m;βmax≤30°,依据观测数据可知最大高差为0.589m,所以

mhAB=±1.4mm,mα=±0.14°

2.3 拟合线的坡度计算

从图3a，3b，3c中可以看出,下割线、上切线、拟合线3种不同的测量计算方式导致坡度的差异,结合式(5),很容易计算出下割线、上切线的坡度。拟合线是在综合考虑最大坡降方向上微地形起伏影响下,通过拟合的方式找出一条比较理想的线来代表该方向上的坡降线,从而确定其坡度。如图3c所示,综合测定最大坡降方向一定长度内微剖面,确定地面的起伏状态,求取地形主要变化点与拟合线之间的高差,按最小二乘原理,使式(11)达到最小,从而确定拟合直线方程式(12),按直线斜率k求取拟合线的坡度。

(11)

H=k*d+b

(12)

其中，H为高程,d为水平距离,k为斜率,b为截距。

3 结果与讨论

3.1 坡度统计分析

从实测的144点最大坡度值来看,下割线最大坡度为36.02°,其对应的拟合线、上切线计算坡度分别为35.26°，32.12°;拟合线最大坡度为35.49°,其对应的下割线、上切线计算坡度分别为35.73°，32.94°;上切线计算最大坡度为36.35°,其对应的下割线、拟合线、坡度分别为35.17°，35.21°。从实测的144点最小坡度值来看,下割线最小坡度为9.17°,其对应的拟合线坡度也为最小值9.23°,而对应的上切线计算坡度分别为7.22°;上切线计算最小坡度为6.93°,而对应的下割线、拟合线坡度分别为10.36°，10.18°。从上面的数据可以看出,每一种测量计算方式坡度最大点都不是同一点,但拟合线与下割线计算坡度差异比上切线与下割线、拟合线计算坡度差异明显小。虽然最小坡度值不尽相同,但下割线与拟合线最小计算坡度值的点相同,而上切线最小计算坡度点与下割线与拟合线的不同,且值相距较大。而上切线计算坡度与罗盘测定坡度测定的是同一切线的坡度,上切线计算坡度最大点为36.35°,其对应的罗盘测定坡度为36.60°,最大罗盘测定坡度点为37.10°,其对应计算坡度为36.19°,虽然点不同,但差异比较小,而最小坡度点为同一点,计算坡度与罗盘测定坡度分别为6.93°，6.60°,且差异比较小,上切线计算坡度与罗盘测定坡度之间差异主要来源与测量误差以及罗盘测量时对直杆平衡条件的影响。虽然4种方法在区域内坡度变化范围差异比较大,但区域内的坡度均值差异较小,所以在以平均坡度来表达某区域的地形条件时,各种方法均可适用。

表1 坡度统计Tab.1 Statistics of slope

3.2 坡度差异对比分析

为了整体反映坡度数据稳定性与不同测量计算方式获得的坡度的差异性,以互差形式对下割线、拟合线、上切线计算坡度和罗盘测定坡度两两求差。

如图4,直观明了反映出来两两互差的极差、中位数、异常值、分布区间等情况,从整体来看,中位数、极差、异常值、分布区间均表明下割线坡度与拟合线坡度差异(a)不明显,两者比较切合;上切线的计算坡度与罗盘实测坡度的差异(f)虽然其中位数、分布区间较为理想,但其极差较大,而且存在偏态,负差异明显,异常值也表现比较突出,从测量过程看应当是存在某种系统性偏差;上切线计算坡度和罗盘实测坡度与下割线坡度和拟合线坡度的差异相比(b，c，d，e),下割线坡度和拟合线坡度与上切线计算坡度差异中位数均偏离0的正方向,而下割线坡度和拟合线坡度与上切线罗盘坡度差异中位数均偏离0的负方向,但4种差异的分布区间大小比较接近,4种差异的极差与异常值表明与罗盘实测坡度的差异更为明显。从以上分析来看,进一步表明罗盘实测坡度的稳定性不强。

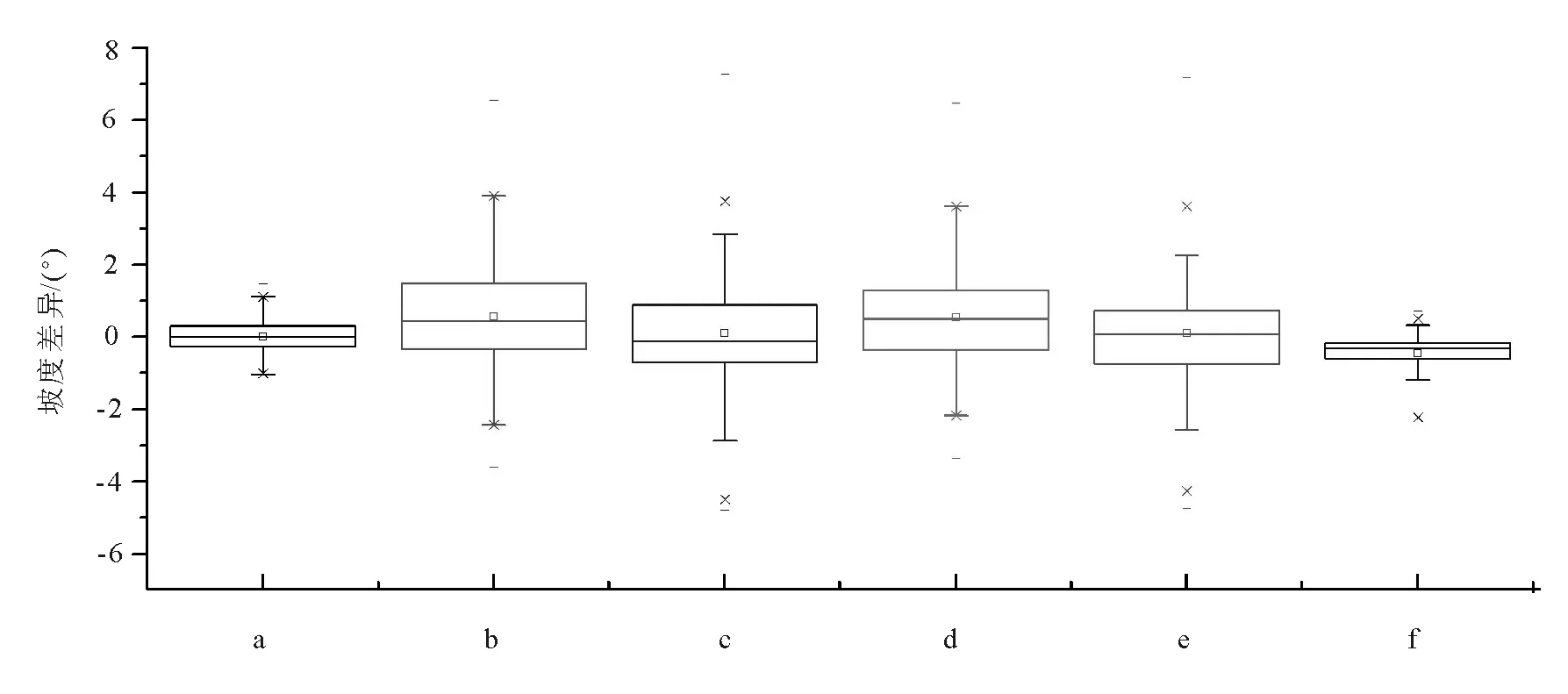
a表示下割线坡度-拟合线坡度互差、b为下割线坡度-上切线计算坡度互差、c下割线坡度-罗盘测定坡度互差、d为拟合线坡度-上切线计算坡度互差、e为拟合线坡度-罗盘测定坡度互差、f为上切线计算坡度-罗盘测定坡度互差。图4 坡度互差箱图Fig.4 Box diagram of slope difference

坡度互差整体分布如图5所示。下割线坡度与拟合线坡度互差最为理想。由于上切线的计算坡度与罗盘实测坡度不存在测量对象的不同,其整体差异除了个别点出现异常外,差异性不明显,但整体偏向于负方向。而其他的4种差异均出现较大的离散程度,差异明显。

a表示下割线坡度-拟合线坡度、b为下割线坡度-上切线计算坡度、c下割线坡度-罗盘测定坡度、d为拟合线坡度-上切线计算坡度、e为拟合线坡度-罗盘测定坡度、f为上切线计算坡度-罗盘测定坡度。图5 坡度互差Fig.5 Slope difference

3.3 微地形对坡度影响

以上分析结果表明,除了测量误差对结果的影响外,地形形态是影响其差异的主要原因。在对144个点的剖面数据综合分析后,考虑中间剖面点相对于两端点的相对高差来看,微地形对坡度测量的影响主要分以下几种情况,如图6所示。

图6a表示在坡向方向剖面图为单一凸形坡,即以两端点连线为基准,中间部分均在连线的上部,在本次试验中占到29.2%;图6b表示在坡向方向剖面图为上凸下凹形坡,即以两端点连线为基准,靠近上部表现为凸起,高于连线,下部表现为凹陷,低于连线,占15.3%;图6c表示在坡向方向剖面图为双凸形坡,即以两端点连线为基准,靠近上部表现为凸起,高于连线,中部表现为凹陷,低于连线,下部表现为凸起,高于连线,但上凸形较为明显,仅占2.1%;图6d表示在坡向方向剖面图为直形坡,即以两端点连线为基准,中间部分几乎在连线上,差异不明显,该地形在7种微地形中所占比例最小,仅为1.4%;图6e表示在坡向方向剖面图为双凸形坡,即以两端点连线为基准,靠近下部表现为凸起,高于连线,中部表现为凹陷,低于连线,上部表现为凸起,高于连线,但下凸形较为明显,所占比例也比较小,为2.1%;图6f表示在坡向方向剖面图为凹形坡,即以两端点连线为基准,中间部分均在连线的下部,所占比例最大,为31.3%;图6g表示在坡向方向剖面图为上凹下凸形坡,即以两端点连线为基准,靠近下部表现为凸起,高于连线,上部表现为凹陷,低于连线,占18.8%。从以上统计结果看,自然坡面发育过程中,从1米空间分辨率的尺度来看,微地形形态主要以凸形坡、凹凸或凸凹坡以及凹形坡为主。

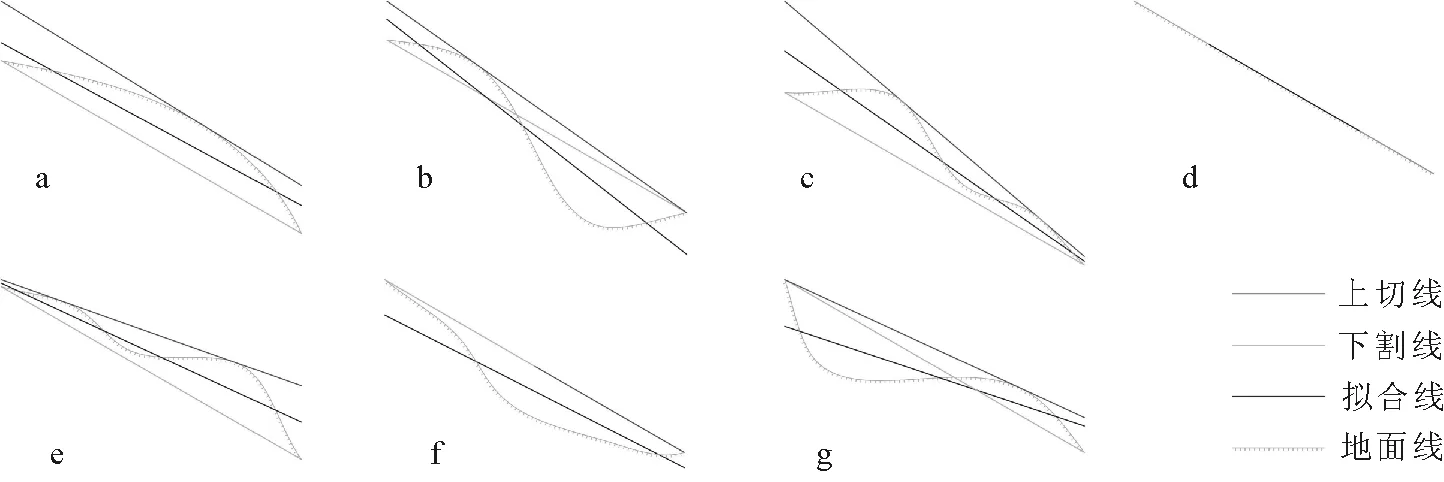
图6 微地形与坡度线关系Fig.6 Relationship between microtopography and slope line

剖面类型 a b c d e f g 数量 42223234527

从图6中可以看出,a，d，f均为单形坡,其余的为双形坡,从测量的角度看,a类型上切线坡度测量时主要依靠重力作用确定平衡状态,稳定性最差,而其他的类型均有两支点,具有良好的稳定性。从测量数据看图7,下割线与拟合线坡度互差最小,均在1.000°范围内,其离散程度也较小。a，e，g类型下割线坡度与上切线坡度均表现出较大的差异性,互差都在1.000°以上,且表现为上切线坡度总体小于下割线坡度。b，c类型下割线坡度与上切线坡度差异虽然没有a，e，g类型表现突出,但差异还是存在,均大于0.14°,分别为-0.317°，-0.888°,总体表现为下割线坡度小于上切线坡度。各类型的上切线坡度与拟合线、下割线坡度差异的离散程度均较大。d类型上切线、下割线和拟合线完整的重合,虽然d类型只有两个,且其坡度数据互差均小于0.14°,以上差异可考虑为直形坡综合因素及测量误差的影响;f类型上切线和下割线重合,且上切线与下割线坡度差异均值为0.073°,以上差异均可考虑为测量误差的影响。

4 结 论

在自然坡面上,通过常规测量方法,分别测定地面线上切坡度、下割坡度及其剖面线的拟合坡度,综合分析结果如下:

1)在表达一定区域内平均坡度时,以罗盘、高差以及拟合方式确定的不同坡度之间差异性较小,均可认为是行之有效的方法,但从互差箱图状态来看,罗盘测定坡度时存在不稳定性因素的影响,表现出部分异常。

2)上切线、下割线、拟合线坡度从稳定性看,下割线、拟合线优于上切线,上切线坡度测量时凸形坡稳定性最差,下割线与拟合线坡度具有较好的吻合程度,拟合线表现出更好的稳定性;凸、双凸(下部凸起明显)、凹凸形类型表现为上切线坡度总体小于下割线坡度;凸凹、双凸(上部凸起明显)形类型总体表现为下割线坡度小于上切线坡度;直线形类型差异主要受直形坡综合因素及测量误差的影响;凹形类型上切线和下割线差异主要为测量误差的影响。

图7 各剖面类型坡度互差雷达图Fig.7 Radar diagram of slope difference by profile type

综上所述，在考虑方便快捷时可以使用罗盘直接指定上切线坡度的方法,当更加注重实测坡度稳定性时,建议以下割线或拟合线作为坡度线间接测定坡度,特别是考虑微地形对坡度的影响时,应以拟合线作为坡度线间接测定。