新能源配电网多运行指标协同的灵敏性分析方法

张庆晖，吴长元，吴杰康，吴 帆，唐惠玲，陈灵敏

(1.广东省城乡规划设计研究院，广东 广州 510290；2.广东工业大学自动化学院，广东 广州 510006；3.广东电网有限责任公司韶关供电局，广东 韶关 512028；4.广西博阳电力勘察设计有限公司，广西 南宁 530028)

0 引 言

电压和网损是电力系统运行指标，电压质量水

基金项目：国家自然科学基金项目(51567002，50767001)；广东省公益研究与能力建设专项资金项目(2014A010106026)；广东自然科学基金项目(S2013010012431，2014A030313509)

平的高低直接反映电网的无功平衡，网损的大小直接反映电力系统节能降耗水平。无功控制和优化的结果影响电力系统无功功率的平衡，进而影响电压质量水平和网损。

对于无功优化问题，国内外许多专家学者近几十年来进行了大量的研究工作，取得了丰富的研究成果，比如线性规划方法[1-3]、非线性规划方法[4-5]、混合整数规划方法[6-8]、动态规划方法[9-11]。线性规划方法通过对优化模型和离散变量进行了线性化和连续化处理，往往导致计算结果与实际值误差较大。非线性规划方法模型直观、精度较高，但计算量较大。混合整数规划方法是一种两步优化方法，问题模型维数增加容易削弱整体最优性，大大增加了计算时间。动态规划方法的数学模型很难与实际问题相匹配，并且随着状态变量数目的增加，动态规划方法的数学模型也变得越来越复杂。

人工智能算法是在一些直观研究的基础上建立起来的一种算法。近年来，由于智能算法能够较好地处理离散变量和非线性问题，因此受到自然有效类比的启发，在电力系统无功优化领域得到了广泛的应用。典型的算法主要有人工神经网络算法[12]、粒子群优化[13-14]、遗传算法[15-17]、模拟退火算法[18-20]。人工智能算法不需要限制性假设来搜索空间。它随机产生初始种群，并根据概率转移原理，采用适当的启发式方法搜索最优解。该算法具有全局优化能力，弥补了传统数学规划方法的不足。对于不同的人工智能算法，由于不同的优化算法和策略，它们具有不同的优化特性。在深入研究每一种人工智能算法的独特优化特性的基础上，通常采用不同算法组合而成的混合智能算法。

下面针对分布式电源接入对配电网电压和网损的影响，通过建立配电网在新能源环境下电压和网损运行指标，构建针对分布式电源和传统无功补偿装置的配电网潮流分布、节点电压和网损的灵敏度矩阵，分析分布式电源大规模接入电网后对电压和网损造成的影响[21]。

1 灵敏度分析方法

1.1 灵敏性指标

在电力系统分析时，通过灵敏度分析方法，分析物理系统中影响电压、网损的变量变化态势和互动、制约关系，进而分析电压和网损对这些变量的敏感程度。按照控制理论，从电压和网损控制的角度看，有控制变量、状态变量和输出变量3种变量。电源有功功率和无功功率、负荷有功功率和无功功率等影响电网的电压和网损，这些控制变量在不同运行方式下总会有微小或大幅的变化，从而导致电网一些相关的状态变量和输出变量也发生微小或大幅的变化。利用灵敏度分析的方法，构建电压和网损对于电源及负荷的有功功率和无功功率等变化的灵敏度指标，通过在不同运行方式下对这些灵敏度指标的计算，可以确定电压和网损的变化情况[21-24]。

1.2 灵敏度矩阵

电力系统在某一运行条件下可由n个非线性网络方程表示，其紧凑形式可表示为

f(x,u)=0

(1)

式中：x为状态变量；u为控制变量。当系统处于稳态运行状态时，式(1)可变为

f(x0,u0)=0

(2)

式中，x0和u0分别为系统稳态运行时的状态变量和控制变量。当系统运行状态变化后，系统稳态平衡方程变为

f(x0+Δx,u0+Δu)=0

(3)

式中，Δx和Δu分别为系统运行状态变化后，状态变量和控制变量的偏差。

利用泰勒级数分析方法，在点x0和u0处展开式(3)，得

(4)

从而得到针对状态变量和控制变量的灵敏度方程[22-33]：

(5)

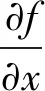
(6)

(7)

式中，S即为灵敏度矩阵。

1.3 潮流的灵敏度矩阵

计及分布式电源的节点功率方程为

ΔPi=PGi+PDGi-PDi-

(8)

ΔQi=QGi+QDGi+QCi-QDi-

(9)

式中：Pi和Qi、PGi和QGi、PDGi和QDGi、PDi和QDi分别为节点i注入的有功功率与无功功率、传统发电机组的有功功率与无功出力、分布式电源输出的有功功率与无功功率、负荷的有功功率与无功功率；QCi为节点i并联电容器输出的无功功率；Vi、Vj、θij分别为电网节点i、j电压大小及两个节点之间电压的相位差；Gij和Bij为电网支路ij的电导和电纳。

设p为扰动变量，则扰动变量、控制变量以及状态变量可表示为：pi=[PDi,QDi]T，ui=[PGi,QCi]T，xi=[θi,Vi]T。因此，假设雅克比矩阵为Jx，潮流的灵敏度方程[22-33]可表示为

JxΔx+JuΔu+JpΔp=0

(10)

由式(9)可得状态变量的偏移量：

(11)

式中：Sxu为状态变量xi=[θi,Vi]T随着控制变量ui=[PGi,QCi]T的变化而发生响应的矩阵；Sxp为状态变量xi=[θi,Vi]T随着系统中负荷的扰动pi=[PDi,QDi]T变化程度的矩阵。

1.4 节点电压灵敏度矩阵

考虑分布式电源及无功补偿装置，节点注入功率表达式为

Pi=PGi+PDGi-PDi

(12)

Qi=QGi+QDGi+QCi-QDi

(13)

节点电压对节点负荷有功功率的灵敏度矩阵[22-33]可表示为

(14)

节点电压对节点负荷无功功率的灵敏度矩阵[22-33]可表示为

(15)

节点电压对节点分布式电源有功出力的灵敏度矩阵[22-33]可表示为

(16)

节点电压对节点分布式电源无功出力的灵敏度矩阵[22-33]可表示为

(17)

节点电压对节点无功补偿无功功率的灵敏度矩阵[22-33]可表示为

(18)

1.5 网损灵敏度矩阵

系统有功网损可表示为

(19)

式中，kij为节点i和节点j间支路变压器变比，若该支路无变压器，则kij=1。

系统网损对无功补偿的灵敏度矩阵[22-33]可表示为

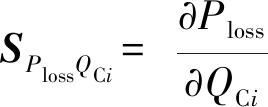
(20)

系统网损对节点分布式电源有功出力的灵敏度矩阵[22-33]可表示为

(21)

系统网损对节点分布式电源无功出力的灵敏度矩阵[22-33]可表示为

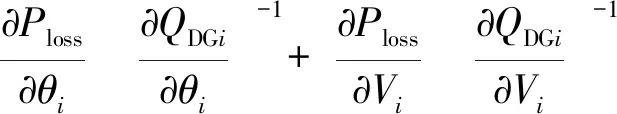
(22)

系统网损对节点注入有功功率Pi和无功功率Qi的灵敏度矩阵[22-33]可表示为

(23)

(24)

式(23)和式(24)可写成如下形式：

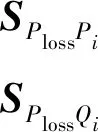
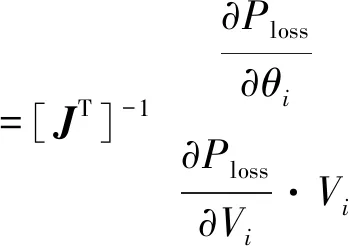
(25)

(26)

(27)

式中，J为牛顿-拉夫逊潮流计算的雅克比矩阵。

2 实例计算与分析

以图1所示的IEEE 30系统为例，分析分布式电源接入电网后对节点电压和网损的影响。考虑DG有功出力分别为20 MW、40 MW和60 MW，接入节点15，对系统节点电压的影响如图2所示，对节点电压偏差的影响如图3所示。由图2和图3可看出，接入分布式电源后，对节点电压的提升作用随着DG出力的增大而增大，而且对接入节点的电压提升作用更明显。

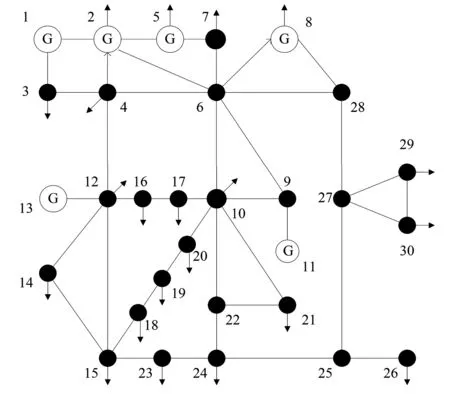
图1 IEEE 30配电系统

图2 分布式电源出力对节点电压的影响

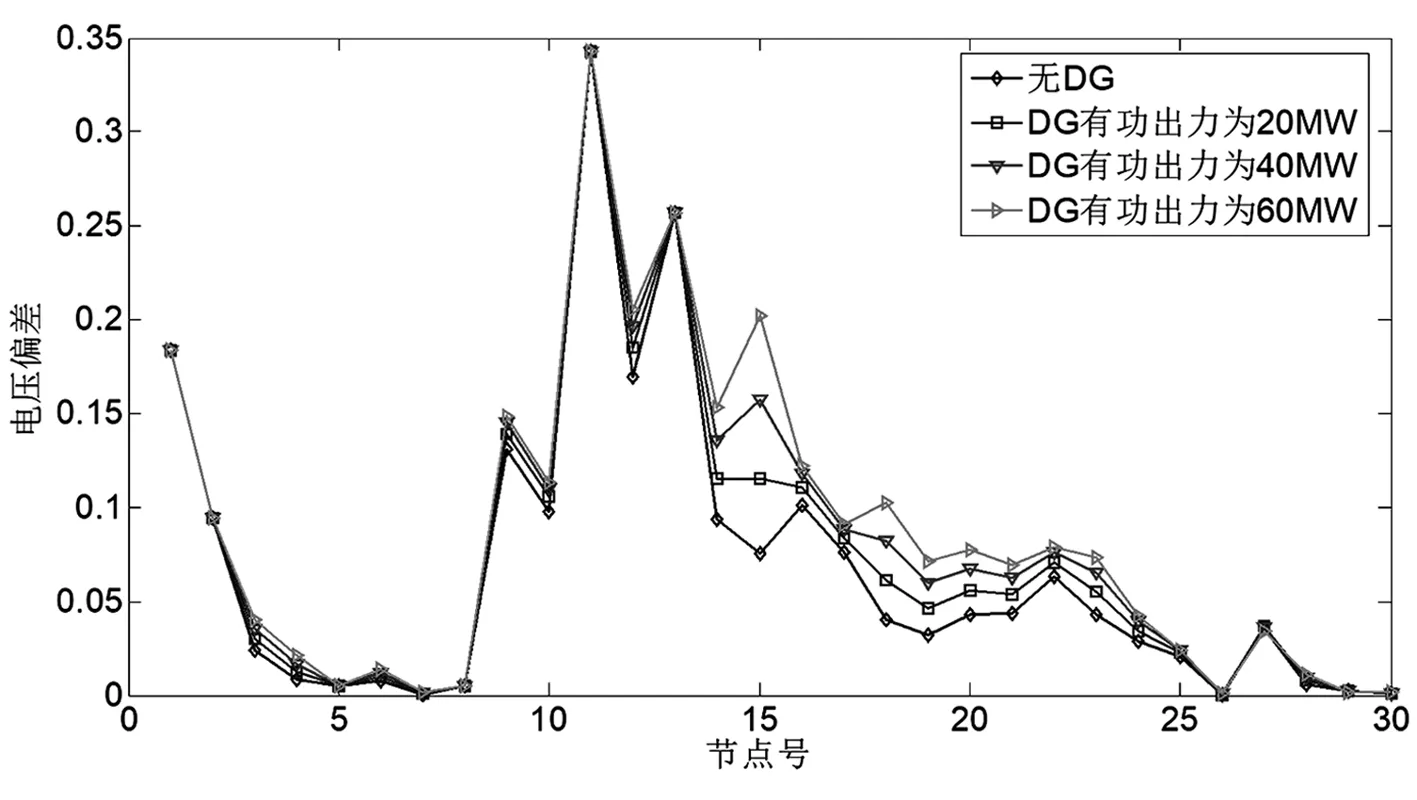
图3 分布式电源出力对节点电压偏移的影响

分布式电源接入电网后对支路有功网损的影响如图4所示。随着DG出力的增加部分支路的有功网损降低，如支路1、2、3、4等；部分支路有功网损增加，如支路22和支路30。分布式电源接入电网后可能增大也可能减小系统网损，这取决于分布式电源接入的位置、其与负荷量的相对大小以及网络的拓扑结构等因素。因此，分布式电源接入电网前必须要根据系统结构和负荷情况，确定最佳接入位置和接入容量。

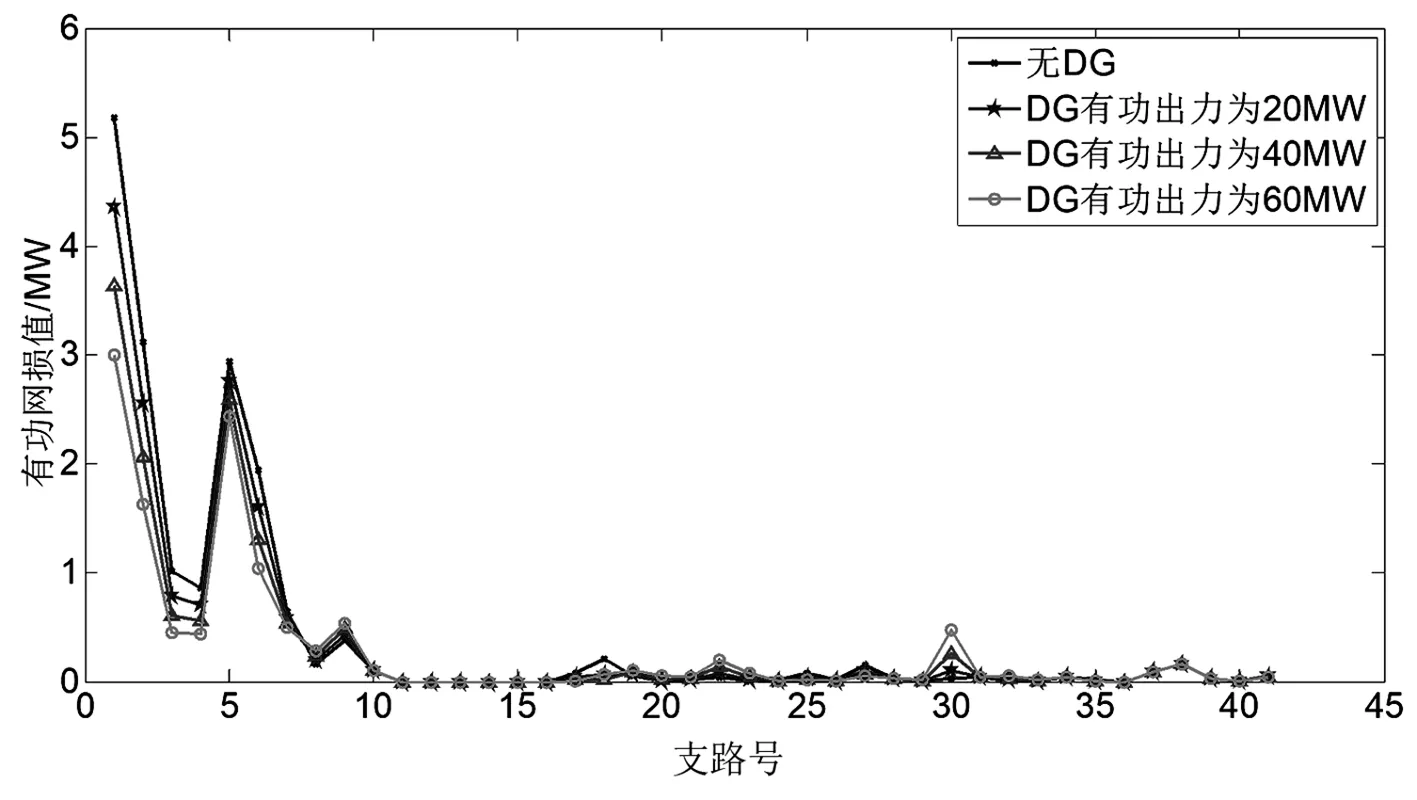
图4 分布式电源出力对网损的影响

3 结 论

前面建立了配电网在新能源环境下电压和网损运行指标，构建针对分布式电源和传统无功补偿装置的配电网潮流分布、节点电压和网损的灵敏度矩阵，分析分布式电源大规模接入电网后对电压和网损造成的影响。通过实例仿真计算，结果表明：

1)配电网电压和网损等指标随着运行方式而变化，在新能源环境下这种变化更具复杂性和不确定性。因此，电压和网损等运行指标协同需要针对不同的配网拓扑结构，并考虑技术和经济的目标要求。受不同的技术和经济指标的制约，电压和网损等指标受到极大的影响。

2)配电网电压在传统无功补偿装置输出无功功率和分布式电源输出有功和无功功率的共同作用下具有较大的灵敏性。要保证电压合格率，需要在不同负荷需求水平下对传统无功补偿装置输出无功功率和分布式电源输出有功和无功功率进行动态协同。

3)在新能源环境下，配电网网损对分布式电源接入位置及有功和无功功率具有较大的灵敏性，分布式电源接入的位置可能增大也可能减小系统网损。