Dashnic-Zusmanovich+矩阵线性互补问题解的误差界估计

余 敏，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)

线性互补问题是一类重要的优化问题,被广泛应用于众多实例中.由于在构建线性互补问题模型的过程中,利用不同算法得到的解会存在一定的误差,因此如何寻找特殊矩阵线性互补问题更小的误差界变得尤为重要.在矩阵理论体系中,H-矩阵占有重要地位,学者们[1-2]研究了H-矩阵及其许多子类矩阵线性互补问题的误差界.笔者拟在文献[3]的基础上,探讨H-矩阵的子类Dashnic-Zusmanovich+矩阵线性互补问题解的误差界.

1 预备知识

文中用Cn×n(Rn×n)表示n×n阶复(实)矩阵集合，并设

定义1[4]设M=(mij)∈Rn×n,q∈Rn,寻找解x∈Rn,使其满足

Mx+q≥0,x≥0,xT(Mx+q)=0.

该问题称为线性互补问题,记为LCP(M,q).

定义2[5]设A=(aij)∈Cn×n,M(A)=(mij),其中mii=|aii|,mij=-|aij|,i≠j,i,j∈N+,则称M(A)为A的比较矩阵.

定义3[5]设A=(aij)∈Cn×n,若存在i∈N+,使得

|aij|(|ajj|-rj(A)+|aji|)>ri(A)|aji| ∀j∈N+,j≠i,

则称矩阵A是Dashnic-Zusmanovich矩阵.

定义4设A=(aij)∈Cn×n，它是对角元素为正的Dashnic-Zusmanovich矩阵,则称A为Dashnic-Zusmanovich+矩阵.

引理1[5]若A=(aij)∈Cn×n，它是Dashnic-Zusmanovich矩阵,则它是非奇异H-矩阵.

引理2[6]设A是H-矩阵,则|A-1|≤(M(A))-1.其中：|A-1|=(|aij|)；A≤B指的是aij≤bij，i,j∈N+.

引理3[7]设M=(mij)∈Cn×n，它是Dashnic-Zusmanovich+矩阵.若A=I-D+DM，其中I是n×n的单位矩阵,D=diag(di),0≤di≤1,i=1,…,n,则A是H-矩阵.

为了方便,引入如下符号:

2 主要结果及其证明

设M是Dashnic-Zusmanovich+矩阵,则M是P-矩阵.由文献[7]可以得到关于M的不等式

其中:I是n×n的单位矩阵;D=diag(di),0≤di≤1,i=1,…,n;x*是LCP(M,q)的解;r(x)=min{x,Mx+q}.

定理1若M=(mij)∈Cn×n，它是Dashnic-Zusmanovich+矩阵,则

证明根据Dashnic-Zusmanovich+矩阵的定义,令A=I-D+DM,其中D=diag(di),0≤di≤1,i=1,…,n,则

(1-di+di|mii|)(1-dj+dj|mjj|-djrj(M)+dj|mji|)>diri(M)dj|mji|.

(1)

由引理3可知A是H-矩阵,由引理2有|A-1|≤(M(A))-1,于是

‖A-1‖∞≤‖(M(A))-1‖∞,(M(A))-1≥O.

(2)

由(1),(2)式可知，

(1-di+di|mii|)yi≤diri(M)yj0+1,

(1-dj0+dj0|mj0j0|-dj0rj0(M)+dj0|mj0i|)yj0≤dj0|mj0i|yi+1，

即

若yi≥yj0,则

若yi

即

可以推出

故有

另一方面，

故有

于是

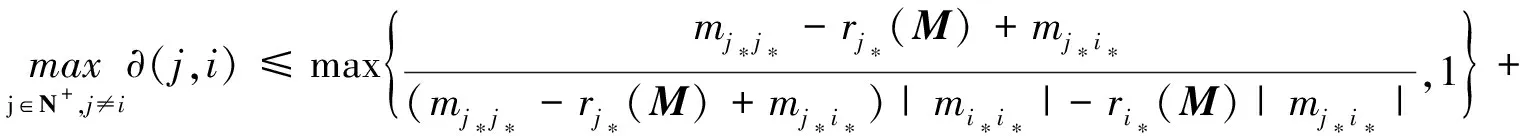
3 实例

令矩阵