SCS模型在无资料地区径流模拟估算中的应用*——以清河流域为例

刘春春，刘万青※，王 宁，杨 波

(1.西北大学城市与环境学院，陕西西安 710127； 2．西北农林科技大学水土保持研究所，陕西杨凌 712100)

0 引言

无资料流域水文计算是长期困扰国际水文学界的难题之一，开展无资料地区水文研究始终是水文工作者的一项重大任务[1]。在23届国际地球物理和大地测量联合会上，国际水文科学协会(IAHS)确定了未来10年的研究重点为无水文资料流域的水文预报(PUB)[2]，该计划为未来无资料地区开展水文研究提供了机遇与发展方向。目前，流域径流模拟估算主要是利用集总式水文模型(IHACRES，Standford，SIMHYD等)、半分布式水文模型(TOPMODEL，HBV，PREVAH，PRMS，SWAT等)、分布式水文模型(MIKE SHE等)开展水文模拟，以及利用数据驱动模型(多元线性回归模型，神经网络模型等)进行数据分析预测[3-4]。

集总式水文模型由于其具有结构简单、参数较少、复杂程度较低等优点，广泛应用于无资料地区的水文模拟。由美国农业部水土保持局开发的SCS(Soil Conservation Service)集总式水文模型实用性强且改进空间大，近年来得到了比较广泛的应用[5]。Amutha和Porchelvan[6]利用SCS模型估算1971—2007年Malattar河子流域逐月径流量及逐年径流量。周翠宁等[7]将SCS模型应用到北京温榆河流域，从年降雨量与径流量的对应关系角度开展研究。刘贤赵等[8]利用SCS模型对黄土高原王东沟流域的降雨径流过程进行模拟，取得了较为满意的效果。张建云等[9]利用GIS手段提取爱尔兰Dodder流域信息，为开展无资料地区SCS模型径流模拟提供一定参考。

为了探索构建便捷的无资料地区水文模拟方法，文章利用SCS模型结构简单，参数较少的优点，将其应用于资料缺乏或无资料地区的水文模拟，并以西安市清河流域为研究对象进行模型应用。此外，为了解决无资料地区水文模型验证问题，该文提出利用径流系数区间法对模拟结果进行验证，这对未来开展无资料地区的径流模拟估算验证可以起到一定的参考作用。同时，清河流域作为西安市周边小流域，是西安市水系调节的重要一环，会对整个城市的水资源规划和防洪决策产生一定影响。因此，开展西安市城市外围小流域的水文研究是非常有必要的。刘春春等[10]基于SWMM模型在该流域模拟了不同降雨条件下的径流过程，可以为防洪减灾提供一定依据，但实际意义并不完整。该文从年际径流角度出发，以SCS模型模拟估算流域径流总量，是对前者研究的重要补充，有助于该流域构建完备的防洪与水资源规划的水安全系统。

1 资料与方法

1.1 研究区概况

清河是西安市灞桥区、蓝田县和临潼区接壤处灞河支流红河的一级支流，位于红河上游两大支流右支。流域形态呈东北—西南走向，流域面积约为26.19km2，流域概况如图1所示。该流域多年平均降水量718.4mm，年内降雨量分布不均匀，降雨主要集中在5—8月份。流域林草覆盖率达80%以上，起到了很好的水土保持功效。目前清河流域为国家水保生态监测系统的一部分，但由于建站时间较短及其他原因，导致实际收集的水文数据时间序列较短，资料相对比较匮乏。

图1 清河流域概况

1.2 数据来源

1.2.1 降雨数据

由于研究区域水文站建设时间较短，缺乏多年降雨量，该文选取流域所在地西安市的历年降雨量作为该实验区的降雨量补充数据，流域缺少年份的降雨数据用西安市平均降雨数据代替。虽然没有对西安市平均降雨数据进行精细化展延、插补等处理，但该数据也可以充分代表西安市总体降雨情况。虽然用西安市的降雨数据替代流域实际降雨量并不能让人感到非常满意，但是该文仅利用SCS模型估算流域的年径流总量，一定程度上降低了对实际降雨量可靠性的依赖程度。

1.2.2 土壤数据

清河流域土壤类型分布图通过野外实测获得，数据来源为西北大学遥感与地理信息系统实验室。流域土壤主要由花岗片麻岩褐土性土、黄土质塿土性土、白墡土、红色土、泥灰岩质紫色土组成。以上各类土壤结合其下渗特点并按照SCS模型土类划分表格可以确定流域的土壤类型。

1.2.3 土地利用类型

SCS模型中不同的下垫面类型产流效果会存在差异。植被覆盖度越高，截留能力越强，土壤下渗量就越大，最终地表的产汇流能力越弱。水体表面雨水没有损失，直接形成径流，因而产汇流能力最强。该文以流域卫星影像分析解译数据为基础，经前期野外实地抽查核实，获得清河流域土地利用现状数据。清河流域土地利用类型如图2所示。

图2 清河流域土地利用类型

表1 清河流域不同前期土壤湿润程度下的CN值

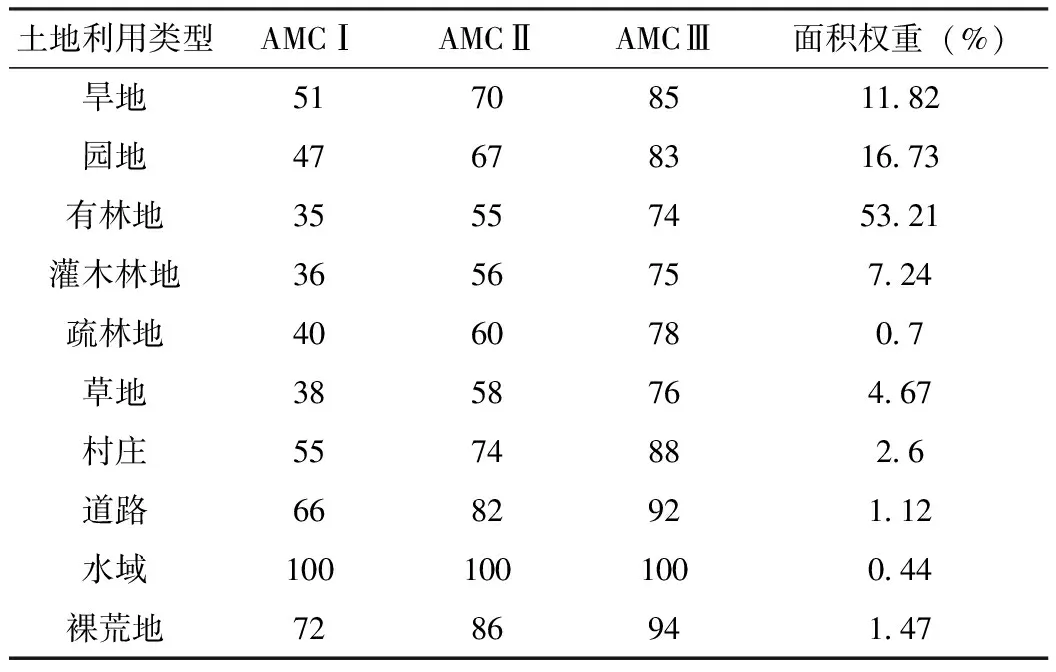
土地利用类型AMCⅠAMCⅡAMCⅢ面积权重(%)旱地51708511.82园地47678316.73有林地35557453.21灌木林地3656757.24疏林地4060780.7草地3858764.67村庄5574882.6道路6682921.12水域1001001000.44裸荒地7286941.47

1.3 研究方法

该文的研究步骤可分为3步：一是确定CN值、λ值等参数； 二是提出径流系数区间法的概念，并通过径流系数取值表计算清河流域的综合径流系数取值范围； 三是利用径流系数区间法对模拟结果进行验证。

1.3.1 SCS模型简介

SCS模型是通过分析大量降雨—径流实测数据建立的经验方程，其径流计算方程为式(1)所示[11]。

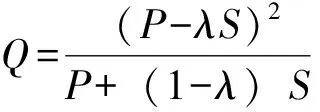
(1)

式(1)中，Q为地表径流深，单位为mm；P为降雨量，单位为mm；λ为初损率；S为径流开始前潜在的最大滞留量，单位为mm。S可由CN值计算得出，如式(2)所示：

(2)

式(2)中，CN值是SCS模型的最主要参数，可以反映出降雨前流域的综合特征。CN值由土壤类型、下垫面类型、土壤前期湿润等级AMC等确定[12]。CN值详细划分标准可参考美国《国家工程手册》[5]。SCS模型依据土壤质地将土壤分为A(透水)，B(较透水)，C(较不透水)，D(不透水)4类。土壤前期湿润程度AMC可以分为AMCⅠ(干燥)、AMCⅡ(中等湿润)AMCⅢ(湿润)。

1.3.2 SCS模型参数的确定

CN值反映不同下垫面的产流汇流能力，用一组曲线予以描述，又可称为径流曲线数[13]。一般情况下，地表产流随CN值增加而增大[14]。以下从土壤类型、下垫面类型、土壤前期湿润程度3个方面确定最终流域平均CN值。参照SCS土壤分类定义表[15]，结合各土类面积和下渗特点，可以确定清河流域以B类土为主。

参考美国水土保持局TR-55手册列出的取值条件[13]，可以确定清河流域不同下垫面的CN值。结合研究区的土地利用类型和土壤类型即可确定AMCⅡ条件下的CN值，利用CN值转换公式即可得到AMCⅠ和AMCⅢ两种条件下的CN值。清河流域不同前期土壤湿润程度下的CN值见表1。

该文是利用历年年降雨总量模拟估算年际径流总量，不是对单场降雨事件的模拟，所以在结合多年降雨数据及土壤含水量的基础上，确定流域的平均前期土壤湿润等级为AMCⅠ[16]。统计不同下垫面的CN值以及下垫面所占面积百分比，进行面积加权平均，即可得到整个区域的平均CN值为40。

大量研究表明λ取值范围一般在0.095～0.38内，美国水土保持局取其平均值0.2 作为λ的值，这是λ的经典取值[17]。SCS模型应用于我国无实测资料的研究中λ取值大都在0.2左右，所以λ取值0.2具有很好的代表性。由于该文是进行年际的径流模拟估算，所以初损率取值比较大，在目前利用SCS模型进行月际或者年际的径流模拟中大都取数值较大的0.2，且取得了不错的模拟效果。该文亦直接采用0.2作为初损率。

1.3.3 径流系数区间法的概念与综合径流系数取值范围确定

由于缺乏流域历年年径流总量数据，故无法从实测角度对模拟结果进行验证。为解决模拟精度分析这一问题，该文采用径流系数法予以验证。传统的径流系数法往往存在选取径流系数值的问题，但是该文没有对研究区域的不同下垫面进行径流系数的实验性确定，单纯的参考类似下垫面的径流系数也会存在一定的误差，为此该文提出一个新的方法，径流系数区间法来进行验证。所谓径流系数区间法就是以不同下垫面的径流系数的波动范围为前提，结合多年年降雨总量，可以计算得出两条多年径流量变化的曲线，这两条曲线是利用径流系数法得到的径流总量变化的区间，如果利用其他方法模拟得出研究区域的多年径流量在两条曲线之间，则说明模拟结果在可接受的范围内，如果需要定量化验证模拟结果，可以利用最大径流量与最小径流量的平均值曲线作为验证标准，判定相对应的吻合程度。

利用径流系数区间法对SCS模型模拟结果验证首先需要不同下垫面的径流系数取值范围作为参考，详见表2。

根据清河流域的特点并结合上述径流系数表，将流域下垫面类型分为a、b、c、d、e 5类，如表3所示。

表2 径流系数ψ[18]

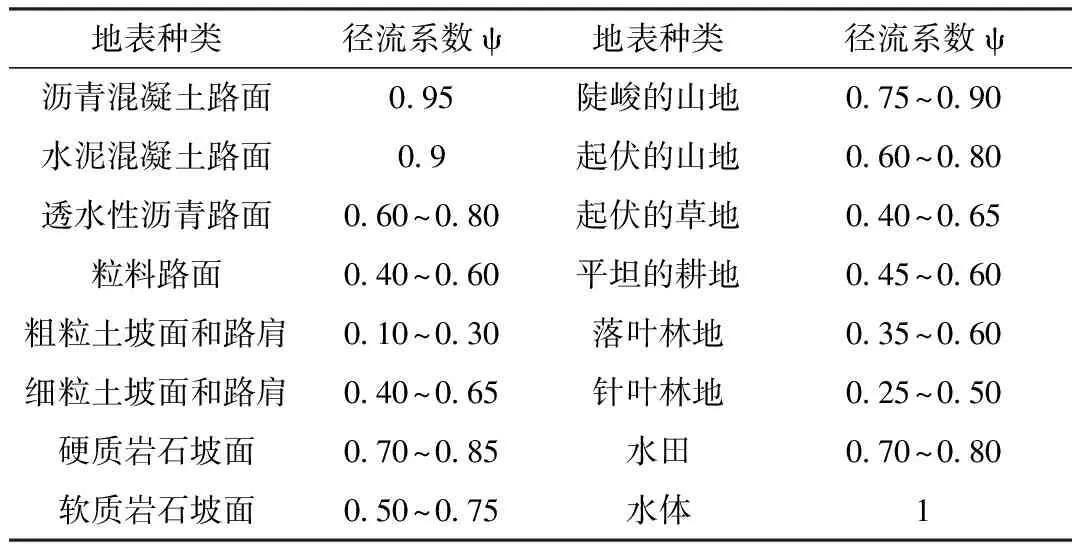
地表种类径流系数ψ地表种类径流系数ψ沥青混凝土路面0.95陡峻的山地0.75～0.90水泥混凝土路面0.9起伏的山地0.60～0.80透水性沥青路面0.60～0.80起伏的草地0.40～0.65粒料路面0.40～0.60平坦的耕地0.45～0.60粗粒土坡面和路肩0.10～0.30落叶林地0.35～0.60细粒土坡面和路肩0.40～0.65针叶林地0.25～0.50硬质岩石坡面0.70～0.85水田0.70～0.80软质岩石坡面0.50～0.75水体1

表3 不同下垫面的重新分类

类别不同下垫面a有林地灌木林地疏林地b草地c旱地园地裸荒地d村庄道路e水域

表4 流域综合径流系数的确定

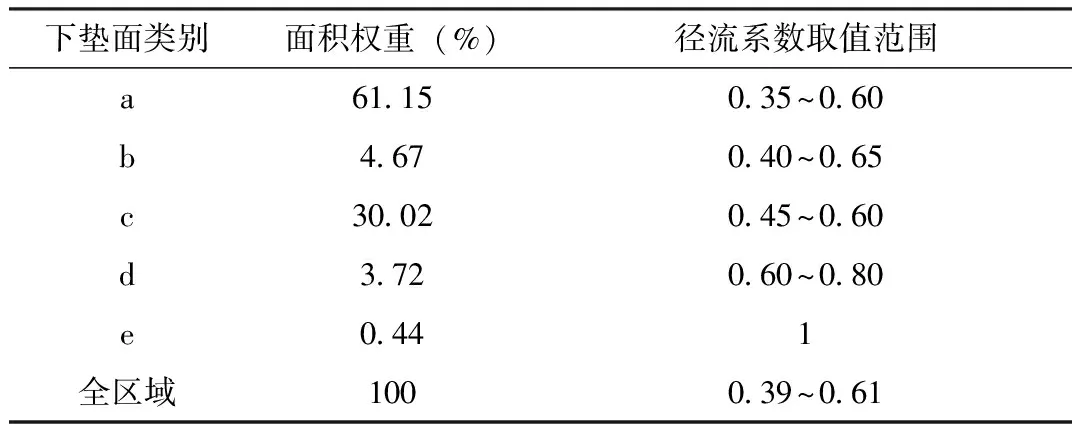
下垫面类别面积权重(%)径流系数取值范围a61.150.35～0.60b4.670.40～0.65c30.020.45～0.60d3.720.60～0.80e0.441全区域1000.39～0.61

a类下垫面以落叶林地作为参考，取值0.35～0.60； b类草地取值0.40～0.65； c类耕地取值0.45～0.60； d类取0.60～0.80； e类水体取值为1。流域综合径流系数由不同下垫面的径流系数取值范围结合面积权重加权得到[19]，结果介于0.39～0.61，如表4所示。

1.3.4 径流系数区间法对模拟结果进行验证

该文首先利用径流系数区间法给出的参考区间来定性的检验SCS模拟结果，判断其模拟结果是否在可接受的范围之内。为了进一步量化的说明模拟结果，该文采用最大径流量与最小径流量的平均值作为标准值，通过查看SCS模型模拟结果与标准值之间的吻合度，来量化的分析模拟结果。该文采用的径流区间可以看成是一个估计值，并不是实际径流量的确切表示。相比其他估计量，样本均值往往是一个更有效的估计量，该平均值应接近或等于真实的参数值[20]。张倩等[21]在无实测资料区域利用径流系数法对SWMM模型模拟结果进行验证时，选取了径流系数取值范围的中间值作为研究区域的综合径流系数，取得了满意的效果。此外，刘昌明等[1]提出在资料稀缺地区将参数进行平均，可以更好地对研究区域进行径流模拟估算。因此，该文选择以最大径流量与最小径流量的算数平均值作为标准值来更有效地估算实际年径流总量。该文以确定性系数(R2)和纳什效率系数(Ens)来评价模型的模拟性能[22]，这两个系数可以反映标准径流量与模拟径流量的拟合度。

(3)

(4)

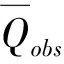
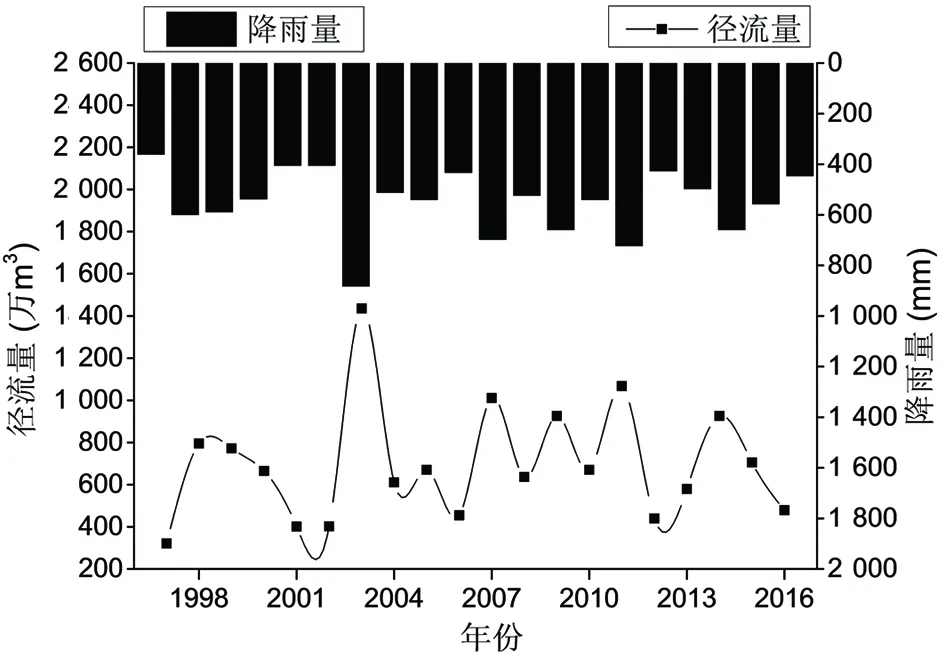
图3 近20年清河流域地表年径流总量

2 结果与分析

2.1 基于SCS模型的径流模拟

通过以上分析，模型参数分别为，CN值取40，λ取0.2，P为流域近20年降雨数据。将各参数带入模型中，即可得到清河流域近20年地表年径流总量。如图3所示。

从图3中可以明显看到，清河流域历年的年径流总量与年降雨总量有很好的对应关系，在不考虑年蒸发量以及地下水损耗的情况下，年降雨量越大，地表径流也越大，其中2003年径流总量最大，达到1 400万m3左右，最小为1997年的300万m3。虽然利用SCS模型初步模拟估算了清河流域的历年地表径流总量，但是其模拟精度与适宜性还有待分析。

2.2 SCS模型的精度分析

利用径流系数区间法给定径流模拟结果的变化区间，可以很好地反映SCS模型模拟结果是否在可以接受的范围内。验证结果如图4所示。

从图4可以看到，SCS模型模拟结果基本都在最大径流量与最小径流量之间波动变化，模拟结果在令人可以接受的范围之内。以上利用径流系数区间法验证了SCS模拟结果为可以接受的正常范围，但是这种结果只是一种定性的表达，为了进一步定量说明模拟结果，该文选择以最大径流量与最小径流量的算数平均值作为标准值来判定SCS模型模拟效果。历年平均径流量与SCS模拟径流量对比分析见图5。

经过计算，SCS模拟径流量与平均径流量的纳什系数为0.6，SCS模拟径流量与平均径流量的确定性系数为0.9，拟合效果较好，这说明利用SCS模型进行地表径流的模拟估算取得了令人较为满意的结果。

图4 基于径流系数区间法的结果验证 图5 平均径流量与SCS模拟径流量对比分析

3 讨论

无资料地区重点是指无水文资料地区，降雨数据可以通过卫星降雨数据或其他遥感数据获得，或者利用临近有水文站的流域插值得到。该文利用西安市部分降雨数据代替流域缺失年份的降雨数据是该文的一个不足之处，但是从根本上这并不妨碍从方法理论上提出利用SCS模型解决无资料地区径流模拟这一问题。当然，如果考虑将该方法在有水文资料的地区试用，在有资料的地区用实测数据进行验证，这样将会使得径流系数区间法更具有科学性。该文选取西安市周边小流域为研究对象，而这些小流域存在水文站缺失、数据不完整等问题，从而在客观上无法有效开展实测资料验证。因此，未来可以考虑在有实测水文资料地区开展更加精确的验证，进一步完善径流系数区间法。

该文的初损率λ取值为0.2，这是大部分地区采用的通用取值。虽然最终的验证结果令人满意，但是在以年际为时间尺度进行径流模拟时，λ的取值还有待深入研究。此外，该文利用传统的径流系数取值表提出径流系数区间法进行模型的验证，虽然不是非常严格的数理论证，但是这也是针对无资料地区进行径流模拟验证时所能想到的比较现实的办法之一。有个有趣的现象就是，SCS模拟结果和径流系数区间法得出的结果有较好的拟合性，其中很大的原因应该就是SCS模型是通过分析大量降雨—径流实测数据建立的经验方程，而径流系数也是经过大量的实测方式得出的经验取值，两者有很好的对应关系。所以，最终的计算结果让人较为满意。

该文的径流系数区间法核心是提出了利用径流区间来判定大致的模拟效果。至于在进行量化验证时，该文采取了取平均值的方式，这种方式是否是最合适的方式，还有待进一步研究。

该文虽然没有利用实测径流总量数据对SCS模型模拟结果进行精确的验证，但是从年际径流角度看，若要进行比较细致充分的验证，至少需要流域10年以上的水文数据作为支撑，这在一些建站时间较短或者水文数据收集不充分的流域开展水文分析是不现实的。当前，我国除了中科院和其他高校下属的一些野外水文站以外，剩余的基本都是水利部下属的水文站。与高校建设的水文站相比，水利部下属的一些水文站存在建站时间较短导致水文数据收集不完整，或者由于工作人员对设备仪器的操作不规范导致实际收集数据存在误差等一系列问题。随着时间的推移，水文数据肯定会越来越丰富，数据的误差会逐渐减小，但是在这数据完善的阶段中，开展流域水文分析的工作并不能停止，开展流域水文分析的目的是要服务于当地水利事业，支持当地的科学发展。为此，该文基于这一现实问题，提出利用SCS模型在无资料地区进行径流的估算，初步进行流域的水文分析，待若干年以后，流域有了较为丰富的数据源以后，结合前期研究成果可以开展更为细致的分析，从而为当地的发展提供更为科学的依据。

4 结论

(1)以清河流域为研究区域，以SCS模型模拟估算流域年际径流总量，模拟结果表明SCS模型适用于清河流域的年际径流模拟估算。研究结果可为当地水资源管理提供一定依据。

(2)该文首次提出利用径流系数区间法对模拟结果进行验证，很好地弥补了无实测资料的不足，对无资料地区的水文验证方法也可起到一个参考的作用。

(3)SCS模型在清河流域的成功应用表明，该模型可以在无资料地区或资料稀缺地区开展径流模拟，由于其结构简单、参数较少等特点，降低了在类似无资料区域开展水文模拟的难度，为此类地区开展水文研究提供了新的途径。