基于贝叶斯模型组合的随机森林预测方法
董娜 常建芳 吴爱国

摘 要:为了能够精准可靠地估计太阳能辐照度,本文提出一种基于贝叶斯模型组合的随机森林算法用于太阳能辐照度预测. 首先,引入K-means聚类和K折交叉验证将气象数据训练集生成多个训练子集,以增加训练子集的多样性并保证均匀采样. 其次,将随机森林作为基学习器建立集成学习预测模型,导入训练子集并训练各个随机森林. 之后,依据各个随机森林在验证集上的预测性能,采用贝叶斯模型组合算法制定组合策略. 个体随机森林在测试集上的预测值经过模型组合策略得到最终输出. 最后,基于气象实测数据建立仿真实验,并引入其他四种预测方法进行对比仿真研究,通过实验结果验证了文中所提出预测方法在太阳能辐照度预测问题中的准确性和可靠性.
关键词:K均值聚类;交叉验证;随机森林;贝叶斯模型组合;太阳能辐照度
中图分类号:TP181 文献标志码:A
Random Forest Prediction Method Based on Bayesian Model Combination
DONG Na,CHANG Jianfang,WU Aiguo
(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
Abstract: To accurately and reliably estimate the solar irradiance, a random forest algorithm was proposed based on the Bayesian model combination for solar irradiance prediction. Firstly, the K-means clustering and K-fold cross validation were introduced to generate multiple training subsets so as to increase the diversity of training subsets and to ensure uniform sampling. Secondly, the random forests were defined as base learners to establish an ensemble learning prediction model,with each training subset being used to train the corresponding individual random forest. Then, according to the prediction performance of each individual random forest on the verification set, the Bayesian model combination algorithm was applied to formulate the combination strategy. The prediction values of individual random forest on the test set were fused to the final output through the model combination strategy. Finally, the proposed method was applied to solve the solar irradiance prediction problem. Simulation experiments were carried out by measured meteorological data. Other four kinds of prediction methods were also introduced to establish the contrast experiments,and the accuracy and reliability of the proposed method in the solar irradiance prediction were verified by comparison results.
Key words: K-means clustering;cross validation;random forest;Bayesian model combination;solar irradiance
太陽能在光热领域和光电领域被广泛应用并被视为最佳代替能源. 季节、气候、云层密度等气候因素引起太阳能辐射量的不确定性制约了其应用领域的发展. 高精度的预测方法一直是太阳能预测研究的热点[1-2].
当前,太阳能辐照度的预测研究主要是使用支持向量机[3-6] (SVM)和人工神经网络[7-9](ANN)算法. 这类学习算法难于平衡训练集的训练误差和测试集的泛化误差之间的关系[10],在训练过程中容易出现过拟合或欠拟合的现象. 然而,在太阳能供热系统的热水供应量估计研究中,保证预测精度的同时预测结果的可靠性显得更为重要[11]. 集成学习为提
高预测结果的可靠性提供了思路. 集成学习(ensemble learning,EL)[12]将多个基学习器组合在一起,常可获得比单个基学习器更显著的泛化性能和可靠性.
本文提出一种基于贝叶斯模型组合的随机森林预测方法(Bayesian model combination-ensemble learning,BMC-EL)用于太阳能辐照度预测,使用随机森林作为基学习器建立集成学习模型. 首先引入K-means聚类[13]和K折交叉验证[14]将气象数据训练集划分为多组训练子集,以增加基学习器输入样本的多样性. 其次导入训练子集并训练各个随机森林. 之后,依据个体随机森林在验证集上的预测精度,采用贝叶斯模型组合[15]算法制定个体随机森林的组合策略. 最后将各个随机森林在测试集上的预测输出依据模型组合策略得到最终太阳能辐照度预
测值.
使用美国气象协会2013-2014年太阳能预测竞赛数据[16]作为数据集,使用经典ANN、SVM 、Multikernel_SVM、K-means_RBF算法建立基于气象数据的太阳能辐照度预测对照实验. 实验结果验证了提出的算法在太阳能辐照度预测研究中的准确性和可靠性.
1 训练子集多样性处理
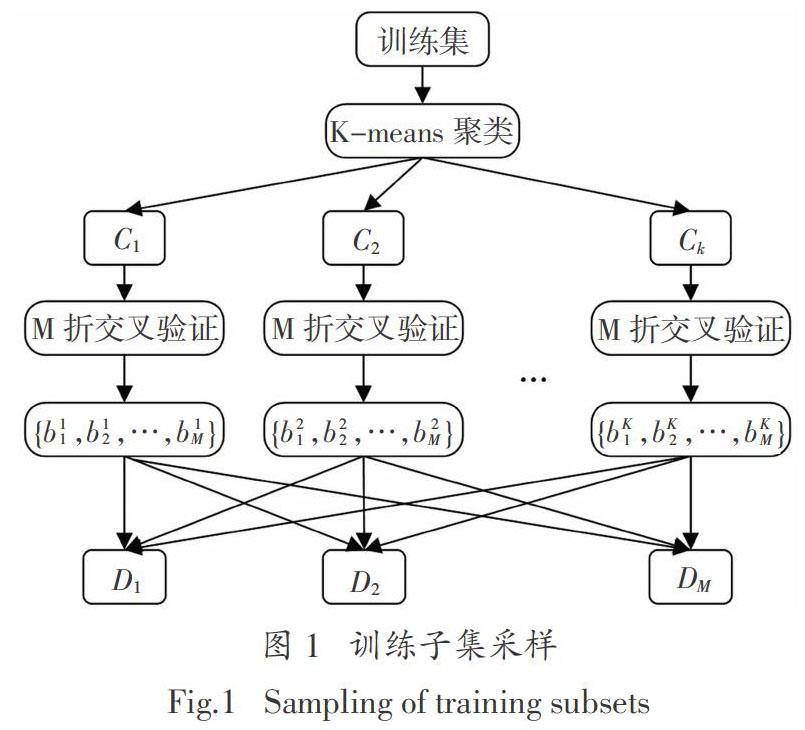
待组合基学习器之间的差异性比较显著时,集成学习模型会拥有更好的性能. 故增加训练子集的多样性以提高基学习器输入样本的差异性. 基于气象数据的太阳能辐照度预测研究中,不同天气状况下气象数据呈现差异性,然而传统随机采样过程会导致训练子集中不同天气状况样本分布不均匀. 针对上述问题,提出K-means聚类和K折交叉验证方法增加训练子集的多样性,如图1.(为了区别K-means聚类和K交叉验证的下标,后文中将K折交叉验证改为M折交叉验证)
假设需要生成M个训练子集{D1,D2,…,DM}. 对K-means聚类生成的簇C1进行M折交叉验证并随机生成M个包{b1,b2,…,bM}. 将{b2,b3,…,bM}导入训练子集D1,将{b1,b3,…,bM}导入训练子集D2,依次将不同的M-1个包导入对应的训练子集,直至将{b1,b2,…,bM-1}导入训练子集DM. 类似地,对簇{C1,C2,…,Ck}都进行M折交叉验证,并分别将其不同的M-1个包导入训练子集{D1,D2,…,DM}.
先聚类再交叉验证,可以使每个训练子集中都包含不同类型天气对应的气象数据,这保证了均匀采样. 交叉验证方法划分训练子集增加了训练子集的多样性.
2 随机森林基学习器
集成学习可以通过组合策略提高预测方法的可靠性. 随机森林中回归树的剪枝操作可以有效降低过拟合的风险,它简单高效,容易实现,计算开销小,在很多分类回归问题中展现出强大的性能. 故本文采用随机森林算法作为基学习器.
本文采用CART回归树建立随机森林的基学习器. 训练集D={(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)},输入样本xi = (x1i,x2i,…,xZi)包含Z个属性变量,输出 Y = (y1,y2,…,yn)為连续值. 回归树的节点对样本xi(1 < i < n)的属性变量j设置切分点s,该输入变量大于s划分为一个区域,否则划分到另一个区域. 对划分得到的区域使用不同的属性变量进一步划分,依据节点的切分点将输入划分为m个区域,分别记为R1,R2,…,Rm. 定义每个区域的输出值分别为:c1,c2,…,cm. 则CART的模型为公式(1):
由上式可得,优化区域Rm的输出值cm可以使得平方误差最小化. 易得当cm 为属于Rm区域的输入样本对应真实输出值的均值时,平方误差E最优,即?觬m = ave(yi|xi∈Rm).
假设选择样本中的变量x(j)为切分变量,节点取值s为切分点. 输入样本中变量j与切分点s比较就可以得到区域R1(j,s)={x|x(j)≤s}和区域R2(j,s)={x|x(j)>s}. 当j和s设为确定值时,区域R1(j,s)和R2(j,s)包含的样本也确定. 故需要确定每个区域的输出值c1和c2使各自区间上的平方差最小,如式(3):
则1 = ave(yi|xi∈R1(j,s)),?觬2 = ave(yi|xi∈R2(j,s)).然后遍历样本中所有的变量,不同切分变量的最优切分点s得到的平方误差最小时记为最优切分变量j. 类似的,对切分好的区域进一步划分,求取最优的切分变量和切分点,最终得到回归树f(x) = ■cm I(x∈Rm).
3 贝叶斯模型组合
3.1 贝叶斯模型平均
贝叶斯模型平均(Bayesian model averaging,BMA)是为解决模型的不确定性而提出的. 它是通过模型在验证集上预测精度的后验概率作为模型的权重,对多个随机森林模型赋以合理的权重,解决单个模型的不确定性和单一性,将多个模型组合到一起的降低风险的方法.
给定数据集D,样本di是由基学习器随机森林的输出值xi和太阳能辐照度真实值yi组成. 模型空间H是由有限个个体假设近似,h作为模型空间的个体假设. 在模型空间和数据集D条件下yi的后验分布为:
式中:p(yi|xi,D,H)为所有个体假设估计yi的后验分布加权平均值, 其中,p(yi|xi,h) = p(yi|θk,h,D)×
p(θk|h,D)dθk为假设空间h对yi的预测分布, θk是
个体假设h对应的参数向量.
通过BMA,数据集D下个体假设h的后验概率(h假设作为数据生成模型的后验概率)p(h|D)可以由式(5)计算:
p(h).p(D|h)=p(D|θk,h)p(θk|h)dθk是个体假设h的积分似然估计,p(θk|h)是h对应的向量参数θk的先验分布,p(D|θk,h)是似然估计. p(h)是个体假设h的先验概率. 虽然集成学习方法中引入训练集采样扰动和属性扰动增加基学习器的差异性,但是为保证所有基学习器都有较高的预测性能,基学习器的初始参数设置并无差异,故先验概率p(h)无需“偏袒”某一个个体假设,本文中p(h)=(k为假设空间中个体假设的数量).
3.2 贝叶斯模型组合
贝叶斯方法在理论上是最优的,并且在许多任务中具有很好的性能. 贝叶斯模型平均也被视为集成学习中结合基学习器的一种标准方法. 然而在贝叶斯模型平均中,积分似然估计的计算方式容易使轻微精度提升的假设获得极高的权重[16],贝叶斯模型平均比stacking更容易过拟合,对模型的近似误差非常敏感,且表现性能更差[17].
为了在太阳能辐照度预测试验中更加高效地获得集成学习的固有优势,组合策略应该侧重地反映各个假设空间的优势互补,而不仅仅是通过贝叶斯模型平均找出最优的假设.
针对上述问题,为贝叶斯模型平均增加假设空间E建立贝叶斯模型组合,将公式(4)修改为式(6):
p(yi|xi,D,H,E) =p(yi|xi,H,e)p(e|D) (6)
式中:e是组合模型空间E中的个体假设模型. 贝叶斯模型平均和贝叶斯模型组合示意图如图2和图3所示.
这样的修正克服了贝叶斯模型平均给个体假设h所有权重的倾向.
4 基于贝叶斯模型组合的随机森林预测
方法
4.1 预测方法流程
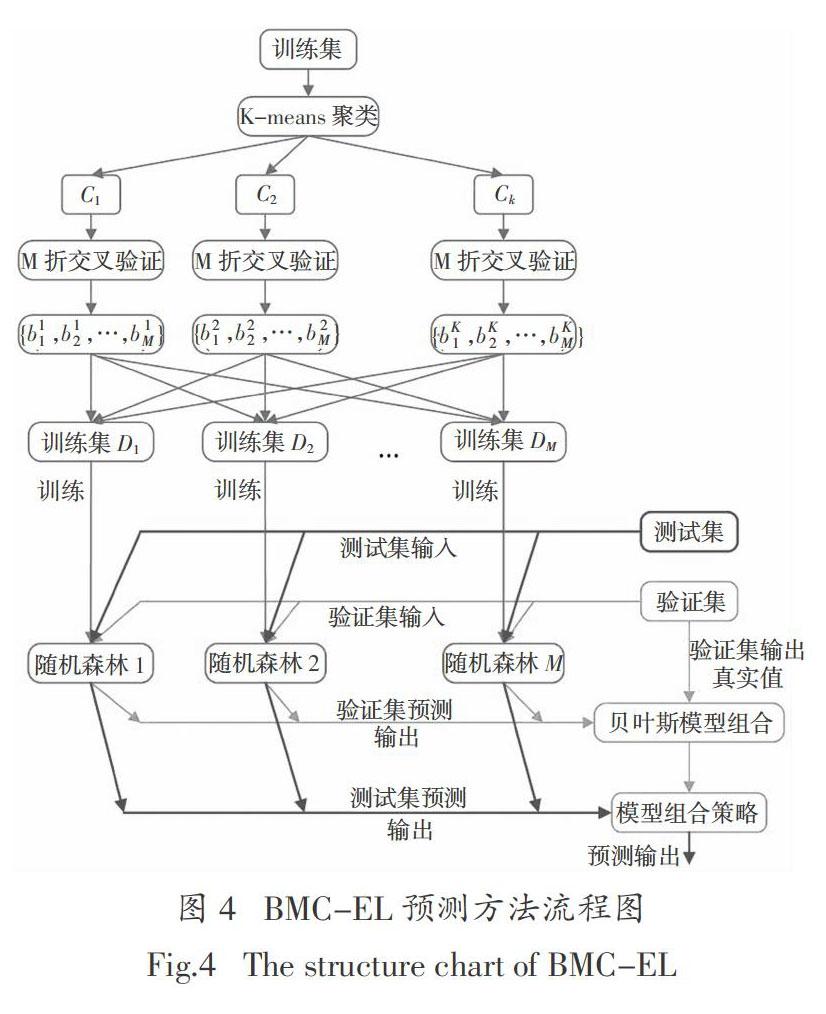
基于贝叶斯模型组合的随机森林预测方法流程图如图4所示.
基于贝叶斯模型组合的随机森林预测方法在太阳能辐照度预测实验中的具体实施步骤如下.
1)首先采用公式x* = 将原始数据归一化处理,对训练集进行K-means聚类操作生成簇划分{c1,c2,…,ck}. 对每个簇ck进行M折交叉验证,并依次生成k个训练子集{D1,D2,…,Dk}. 采用K-means聚类和M折交叉验证划分训练子集,同时保证了训练子集的多样性和均匀采样.
2)使用多个CART回归树构建随机森林,将k个训练子集训练k个随机森林算法.
3)向训练好的k组随机森林导入验证集,输出k组预测输出值(y1,y2,…,yk). 假设验证集的真实输出值为y,构建矩阵(y,y1,y2,…,yk)并导入贝叶斯模型组合方法,根据k组随机森林在验证集的预测性能输出模型组合策略.
4)向训练好的k组随机森林导入测试集,个体随机森林输出各自模型预测值(y1,y2,…,yk),则集成学习方法的预测输出为p(Y|yk,D,H,E)=p(yi|xi,H,e)p(e|D).
4.2 预测方法的复杂度分析
CART回归树在寻找切分节点时需要遍历当前特征的所有可能取值. 设数据样本具有F个特征,每个特征有N个切分点,CART回归树共生成
S個内部节点,则CART回归树的时间复杂度为
O(F*N*S).
设每个随机森林基学习器中包含M个CART回归树,集成学习预测方法中共包含了K个基学习器,则集成学习的时间复杂度为O(F*N*S*K*M).
在训练子集采样部分,设k个聚类中心,每个样本包含F个特征,聚类中心的迭代次数为t,则K-means聚类的时间复杂度为O(k*F*t). 设每个簇包含m个样本,则训练子集采样过程的时间复杂度为O(k*F*t+m*M).
贝叶斯模型平均包含h个体假设,验证集包
含c个样本,则贝叶斯模型平均的算法复杂度为
O(c*h). 贝叶斯模型组合的假设空间E包含e个体假设,则贝叶斯模型组合方法的时间复杂度为
O(c*h*e).
由于切分点个数N较大,故集成学习的时间复杂度远大于训练子集采样和贝叶斯模型组合. 所以基于贝叶斯模型组合的随机森林预测方法的时间复杂度大于集成学习方法,训练子集采样和贝叶斯模型组合的时间复杂度相对较小.
5 太阳能辐照度预测实验
5.1 性能指标
均方误差(MSE)和绝对平均误差(MAE)作为太阳能辐照度预测的误差评价指标,本文额外定义了平均误差率(Average Error Rate,AER)和误差率小于0.1的预测成功率(Rate of success,RS)两个评价指标,如公式(7)~(9):
式中:Ypre是预测输出;Yreal是真实值;Er是每个预测样本的误差率;AER为平均误差率;Num为预测结果的样本数;RS表示精确预测样本的百分比,它反映了预测结果的可靠性.
5.2 训练子集多样性
将原始气象数据归一化处理,然后对训练集进行K-means聚类操作. 太阳能辐照度预测实验中将训练集分为10个簇{C1,C2,…,C10}. 取输入样本的dswrf_sfc,dswrf_sfc,tmp_sfc三个属性建立三维坐标系,簇中的样本在坐标系中分布如图5所示. 属性参数范围经过归一化处理到[-1,1]区间.
分别对上述划分的簇进行10折交叉验证,将其中不同的9个包分别导入各个训练子集. 4个训练子集的气象样本分布如图6所示. 由于聚类后又采用10折交叉验证,训练子集的样本量为训练集的90%. 由4个训练子集的样本分布图可得,采样过程并未影响不同天气状况的样本分布. K-means聚类和M折交叉验证结合的采样过程不仅保证了均匀采样,同时增加了训练子集的差异性.
5.3 模型误差估计及参数设置
随机森林回归模型是通过袋外数据(OOB)来估计模型误差的. 随机森林回归模型中Bagging采样理想状态下会有37%的数据未被抽取,则将这些样本进行模型的误差估计. 由于随机森林算法本身的属性扰动,只有当CART回归树的数量达到一定量级时,随机森林才会收敛到更低的泛化误差. 将所有气象预报样本导入单个随机森林算法,记录OOB误差与回归树数目之间的关系如图7所示.
由图7可知,当CART回归树的数量到达200时,随机森林的OOB误差趋于收敛. 将太阳能辐照度预测实验中随机森林模型CART回归树数目设置为200. 在太阳能辐照度仿真试验中,集成学习模型设置10组随机森林,对应上述10组训练子集,对照实验参数设置如表1所示. 对照实验中EL预测方法训练子集使用完整训练集,模型组合策略采用贝叶斯模型平均,其他设置与贝叶斯模型组合的随机森林预测方法一致.
5.4 实验结果
本章将HOBA中尺度站的太阳能辐照度和周围GEFS站点的气象数據作为数据集(2008年之后的太阳能辐照度未公开),1994年1月1日~2004年12月31日的样本作为训练集. 使用随机函数(randvector,MATLAB)为聚类和交叉验证处理过的训练子集重新排序,缓解相似的气象预测样本在训练时接连出现. 将2005年1月1日~2006年12月31日的样本作为验证集. BMC-EL基于验证集制定模型组合策略,对照实验中利用验证集优化预测模型的超参数. 将2007年全年的气象预报样本作为测试集,用于太阳能辐照度预测实验. 对照实验中各类预测方法的太阳能辐照度输出值如图8所示.
图8中,对照实验中各类预测方法的预测曲线和真实曲线有相近的变化趋势. 然而各类预测方法在太阳能辐照度连续波动较大的样本出现较大的误差. SVM和Multikernel-SVM算法在太阳能辐照度预测中分别出现了过拟合或欠拟合. 其中,BMC-EL虽然也出现了较明显的偏差,但由于贝叶斯模型组合策略,其预测曲线更接近真实曲线.
为了直观地展示各类算法的预测误差,对照实验中太阳能辐照度预测输出的误差曲线如图9所示,其中BMC-EL方法预测误差曲线波动最小. 各类预测方法在2007年7月30日的太阳能辐照度预测时出现极大的偏差,最大的预测偏差近20 MJ·m-2,然而BMC-EL此处的偏差略小于10 MJ·m-2. 由于贝叶斯模型组合是从不同的模型空间中选择最好的模型组合策略,故BMC-EL算法在一些较难预测的样本上依然保证了稳定的预测精度. 贝叶斯模型组合策略极大地提高了预测方法的可靠性.
在坐标系中绘制y = x的直线表示预测辐照度和真实辐照度完全相同. 在散点图中样本点距离y = x直线的距离越远则误差越大. 将各类预测方法在测试集上的预测输出和真实输出绘制到坐标系中,如图10所示.
图10中BMC-EL预测方法对应的散点更加集中,并且更加贴近于y=x直线. 在BMC-EL的预测样本中,在太阳能较为丰富的气象条件下(晴,无云)散点最为集中,预测精度最高;太阳能辐照度匮乏的天气(阴,雨,多云,仪器无读数)包含了复杂的非线性,各类预测方法在气象条件糟糕的样本中都出现较大的偏差,而BMC-EL在这类样本点的预测偏差最小,它通过贝叶斯模型组合策略有效地提高了预测方法的可靠性.
各类预测方法在测试集在不同月份的平均性能指标如表2所示.
综述太阳能辐照度预测实验结果,基于贝叶斯模型组合的随机森林预测方法在太阳能辐照度预测研究中具有非常好的预测性能,可靠性强,对不同的天气状态下的太阳能辐照度都能实现精确可靠的预测.
6 总 结
本文提出一种基于贝叶斯模型组合的随机森林方法用于太阳能辐照度预测,首先引入K-means聚类和M折交叉验证将气象数据训练集生成多组彼此相交且不相同的训练子集,以增加随机森林输入样本的多样性. 其次将多组训练子集导入并训练集成学习模型中的个体随机森林. 之后,将多组随机森林在验证集上的输出结果输入贝叶斯模型组合算法,依据验证集上预测性能的后验分布制定随机森林模型的组合策略. 最后各个随机森林在测试集上的预测输出经模型组合策略输出太阳能辐照度预测值. 在太阳能仿真实验中,BMC-EL方法通过增加贝叶斯模型组合方法显著减少了单个随机森林算法的不确定性,增加了太阳能预测输出的可靠性. 多组辐照度预测实验结果证明了所提出的预测方法预测精度高,可靠性强,可以精确可靠地预测不同气象环境中的太阳能辐照度.
参考文献
[1] 田翠霞,黄敏,朱启兵. 基于EMD-LMD-LSSVM联合模型的逐时太阳辐照度预测[J]. 太阳能学报,2018,39(2):504—512.
TIAN C X,HUANG M,ZHU Q B. Hourly solar irradiance forecast based on EMD-LMD-LSSVM joint model[J]. Acta Energiae Solaris Sinica,2018,39(2):504—512.(In Chinese)
[2] 路志英,任一墨,葛路琨. 基于样条估计分位数回归的光伏功率回归模型[J]. 湖南大学学报(自然科学版),2017,44(10):91—98.
LU Z Y,REN Y M,GE L K. Photovoltaic power regression model based on spline estimation and quantile regression[J]. Journal of Hunan University (Natural Sciences),2017,44(10):91—98.(In Chinese)
[3] YANG X,JIANG F,LIU H. Short-term solar radiation prediction based on SVM with similar data[C]// Renewable Power Generation Conference. IET,2014:1.11—1.11.
[4] GUO W,MINGJIA L I,TAO L I,et al. Parameter identification of Hammerstein ARMAX model based on APSO-WLSSVM algorithm[J]. China Science Paper,2018,13(2):136—142.
[5] ALAM S,KANG M,PYUN J Y,et al. Performance of classification based on PCA,linear SVM,and multi-kernel SVM[C]//Eighth International Conference on Ubiquitous and Future Networks. IEEE,2016:987—989.
[6] ZHOU Y,CUI X,HU Q,et al. Improved multi-kernel SVM for multi-modal and imbalanced dialogue act classification[C]//International Joint Conference on Neural Networks. IEEE,2015:1—8.
[7] RABBI K M,NANDI I,SALEH A S,et al. Prediction of solar irradiation in Bangladesh using artificial neural network (ANN) and data mapping using GIS technology[C]//2016 4th International Conference on the Development in the in Renewable Energy Technology(ICDRET). IEEE,2016:1—6.
[8] ANAMIKA,KUMAR N,AKELLA A K. Prediction and efficiency evaluation of solar energy resources by using mixed ANN and DEA approaches[C]// Pes General Meeting | Conference & Exposition. IEEE,2014:1—5.
[9] YADAV A K,MALIK H,CHANDEL S S. ANN based prediction of daily global solar radiation for photovoltaics applications[C]//India Conference. IEEE,2016:1—5.
[10] CHEN L G,CHIANG H D,DONG N,et al. Group-based chaos genetic algorithm and non-linear ensemble of neural networks for short-term load forecasting[J]. Iet Generation Transmission & Distribution,2016,10(6):1440—1447.
[11] BAILI H,LI Y F. Online reliability prediction of energy systems with wind generation[C]//International Midwest Symposium on Circuits and Systems. IEEE,2016:1—4.
[12] KROGH A,VEDELSBY J. Neural network ensembles,cross validation and active learning[C]//International Conference on Neural Information Processing Systems. MIT Press,1994:231—238.
[13] ALOISE D,DESHPANDE A,HANSEN P,et al. NP-hardness of Euclidean sum-of-squares clustering[J]. Machine Learning,2009,75(2):245—248.
[14] 劉芳,夏洪山,艾军,等. 基于氧化动态模型的沥青热氧老化性能预测[J]. 湖南大学学报(自然科学版),2018,45(1):136—141.
LIU F,XIA H S,AI J,et al. Prediction of asphalt thermal oxidative aging performance based on oxidation dynamic model[J]. Journal of Hunan University (Natural Sciences),2018,45(1): 136—141. (In Chinese)
[15] MONTEIH K,CARROLL J L,SEPPI K,et al. Turning Bayesian model averaging into Bayesian model combination[C]//International Joint Conference on Neural Networks. IEEE,2011:2657—2663.
[16] AMS 2013-2014 Solar energy prediction contest,forecast daily solar energy with an ensemble of weather models[EB/OL]. https://www.kaggle.com/c/ams-2014-solar-energy-prediction-contest.
[17] CLARKE B. Comparing Bayes model averaging and stacking when model approximation error cannot be ignored[J]. Journal of Machine Learning Research,2003,4(4):683—712.

