电磁脉冲辐射环境仿真分析研究

马继峰 周春梅

1.宇航智能控制技术国家级重点实验室，北京 100854 2.北京航天自动控制研究所，北京 100854

飞行器电子设备受外界电磁干扰的途径主要有传导耦合和辐射耦合，其耦合路径包括天线、金属壳体孔缝、电缆和电源等。其中，针对壳体进行屏蔽是一种有效的抑制电磁干扰手段，屏蔽包括低频段的电屏蔽和磁屏蔽及高频段的电磁屏蔽。在低频段，材料及接地是影响屏蔽效能的主要因素。随工作频率的增高，金属壳体材料及厚度的影响变为次要，主要因素是金属壳体的孔缝耦合。电磁波的孔缝耦合是一个经典的电磁问题，也是值得研究的一类工程问题[1-4]。

电磁脉冲的孔缝耦合问题研究由来已久，计算孔缝耦合也有多种方法，其中比较典型的理论有以下几种：应用Bethe理论进行分析、衍射理论、电磁对偶原理及等效电路法。

近几年，随着计算机技术的飞速发展，用数值方法解决电磁脉冲的孔缝耦合问题取得了长足的进展，目前主要有如下3种方法：有限元法(FEM)、时域有限差分法(FDTD)和传输线矩阵法(TLM)。这些方法各有特色，能够有效评估强电磁脉冲对电子设备金属壳体上孔缝结构的耦合作用，为进一步的工程防护设计提供了依据[5-6]。

1 典型电磁场数值计算方法原理

下面简单介绍与研究工作相关的有限元法(FEM)、时域有限差分法(FDTD)和传输线矩阵法(TLM)的基本原理。

1.1 有限元法

有限元方法(FEM)是求解数理边值问题的数值技术。该方法首先被应用于弹性力学问题，取得了成功。近年来，该方法广泛应用在多个工程领域里，解决多类数学物理问题，其中包括电磁场问题。

针对电磁场问题采用有限元法求解的主要途径包括：1)从与所解微分方程的变分方程出发，通过变分原理导出有限元方程进行求解；2)采用加权余量法，直接用微分方程求导出有限元方程。

有限元方法是求边值问题的数值过程，该方法采用多个子域表示整个连续区域。在每个子域中，未知函数采用带有未知系数的插值函数表示，把具有无限个自由度的边值问题转化成有限自由度问题。然后，采用变分方法得到一组代数方程。最后，求解方程组得到边值问题的解。一般地，边值问题的有限元分析包含子域的划分或区域的离散、选择插值函数、建立单元特征、建立方程组和求解方程组等。

1.2 时域有限差分法

时域有限差分法(FDTD)是求解微分方程的常用方法，用差分方法直接求解时变麦克斯韦(Maxwell)方程组的方法称为电磁场的时域有限差分法。该方法经过30多年己发展为成熟的数值方法，应用范围越来越广。

对于电磁波孔缝耦合问题，一般都把孔缝设定为方形或圆形，而且这些孔缝分布在无限大的导电体薄壁上。对于不规则形状的、开在有限尺寸的物体表面上的或者与物体内腔相通等复杂的孔或缝，解析方法和传统的数值方法并不适用。时域有限差分法恰好能够模拟复杂的电磁结构，在解决复杂对象的电磁场分布问题上具有一定的优势，因此在电磁脉冲的孔缝耦合研究中也有一定的应用。

1.3 传输线矩阵法

传输线矩阵法(TLM)是一种采用时域微分的数值计算方法针对电磁场问题进行时域分析的方法[6],可以用于模拟电磁波的传播、散射特性。该方法的理论基础是惠更斯的关于波的传播原理，并将连续的波按时间离散，通过研究离散的波在不同导波结构中的传播情况获得导波结构的种种传输特性。

2 算法和软件的选择

2.1 传输线矩阵法的选择

近几年，传输线矩阵法在误差纠正、节点简化等方面进行了改进。随着计算能力的提高，传输线矩阵法中引入了网络分解技术、差分技术和数字信号处理技术等，使得该方法的应用领域越来越广泛。传输线矩阵法从理论上可以解决所有的电现象．但求解有些问题的算法是非常复杂的。

电磁脉冲仿真的问题通常是求解带宽较宽，还要给出时域分析结果，因此对算法和软件选择提出了约束。从CPU的时间和内存耗费上看，频域算法FEM需要的CPU时间和内存耗费分别与网格数的平方和二次方成正比，而时域算法因为是时间迭代过程，不需要进行矩阵求逆，所以仿真需要的CPU时间和内存耗费几乎和网格数成正比关系。

首先，从计算结果的给出形式来看，由于频域算法每次只给出一个频点的计算结果，要获得结构的宽带特性，就需要进行多次反复计算。而时域算法一次计算可以求解完整频带内的电磁特性，并给出时域波形，因此是此类电磁脉冲计算的首选；其次，相关研究表明，传输线矩阵法比传统的时域有限差分法在计算精度上有很大的提高[6]，因此选定传输线矩阵法进行电磁场特性的仿真分析。

2.2 CST MS软件的选择

在电磁脉冲辐射场对设备壳体的耦合分析中，选用CST软件中的MS工作室进行建模仿真。

CST软件是由德国的CST公司设计的专业电磁场仿真软件，是专门面向三维电磁场设计、分析的仿真工具，能够覆盖各种典型电磁场和多频段的时域、频域仿真分析。

3 时域、频域算法的对比仿真分析

为准确分析电磁脉冲辐射场对飞行器系统电子设备等的电磁耦合效应，对比理论计算与仿真软件分析的差异情况，分析不同数值算法在孔缝耦合电磁分析上的适用情况，开展了对比仿真工作。

3.1 仿真建模及硬件配置

孔缝耦合特性分析本身具有较好的普遍性和通用性，以一个简化的立方体金属壳体为例，壳体内部尺寸为225mm×136mm×16mm，机壳厚度为4mm，上下盖板为1.9mm，材料属性为金属铝，电导率为3.54×107S/m。因盖板与壳体结合紧密，它们之间的细缝结构尺寸非常小。为了比较分析仿真计算采用的传输线矩阵法的计算效率和准确度，将机壳和盖板间缝隙设为较苛刻的0.1mm。

3.2 封闭腔体谐振频点的理论分析和本征模求解对比

3.2.1 谐振点理论计算

根据电磁场理论，金属腔体的谐振频率与其结构的几何尺寸有关，其谐振波的谐振频率为：

(1)

其中，c为光速；m、n和p为谐振模式，分别为0，1，2…，其中m、n不能同时为0；a、b和h为腔体尺寸。

根据上式，计算得出225mm×136mm×16mm封闭腔体在2GHz以下各个模的谐振频率为f110=1.29GHz和f210=1.72GHz

此时壳体的Q值理论上为无穷大，在频谱上即为在2GHz以内2条单独的谱线，其频点对应计算所得的2个谐振频率。

3.2.2 本征模求解计算

为了验证以上结果，使用CST微波工作室的本征模求解器对壳体进行仿真。计算模型如上所示，在微波工作室中单位设为mm/GHz/ns，背景材料设为Normal，边界条件为电壁，设置频率范围为0到2GHz。对前述尺寸的金属腔体进行建模，启动本征模求解器。

通过仿真计算，得到谐振频率的统计计算结果如图1。

图1 本征模求解计算结果

从图1的计算结果可以看出，2GHz以下的谐振频点为模式1和2，频率分别为1.29GHz和1.72GHz，与理论分析完全一致，仿真计算结果具有可信度。

通过本征模求解还可以查看模式1和2的电磁场分布，从而确定其谐振场的分布，其分布场如图2所示。

图2 模式1的电场分布图

图3 模式1的磁场分布图

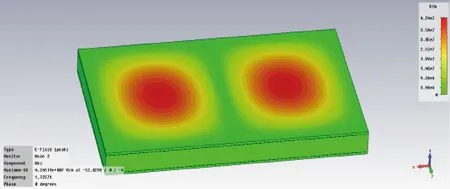
图4 模式2的电场分布图

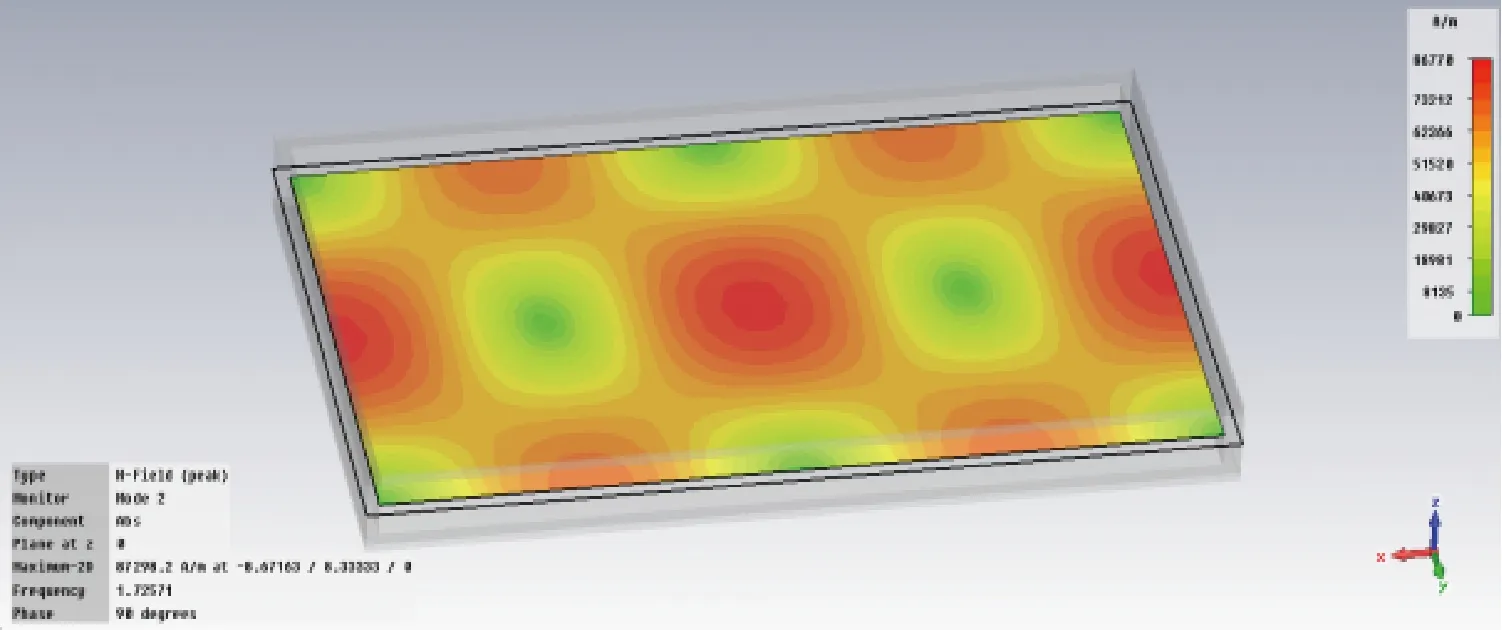
图5 模式2的磁场分布图

从模式1和2的电场分布图可以清晰地看出，2个谐振模式与理论计算模式完全一致。二者的相互印证，对后续深入开展电磁脉冲辐射环境的建模仿真分析与仿真可信度分析提供了必要保障。

4 小结

电磁脉冲辐射环境仿真涉及到各种复杂的空间辐射模型，本文选取简化的壳体孔缝耦合模型，使用CST微波工作室软件和谐振点理论计算2种方法进行了仿真结果对比与印证，为后续建立基于自研+商业软件的辐射环境综合集成仿真软件系统奠定了基础。该软件将进一步扩展应用于研究分析飞行器及其设备的电磁脉冲辐射效应，从而为辐射防护手段的设计与效果分析提供理论依据和指导。